沪科版八年级数学下册 2024-2025学年八年级下册数学专项训练卷(二)docx(含答案)
文档属性
| 名称 | 沪科版八年级数学下册 2024-2025学年八年级下册数学专项训练卷(二)docx(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览



文档简介
专项训练卷(二)
训练内容:勾股定理 时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40分)
1. 一个三角形的三边长分别为 2ab,则这个三角形的形状为 ( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
2. 下列条件中,能判断一个三角形是直角三角形的是 ( )
A.三边长为2, , B.三个角满足关系2∠B+2∠C =∠A
C.三条边的比是2:3:4 D.三个角的比是3:4:5
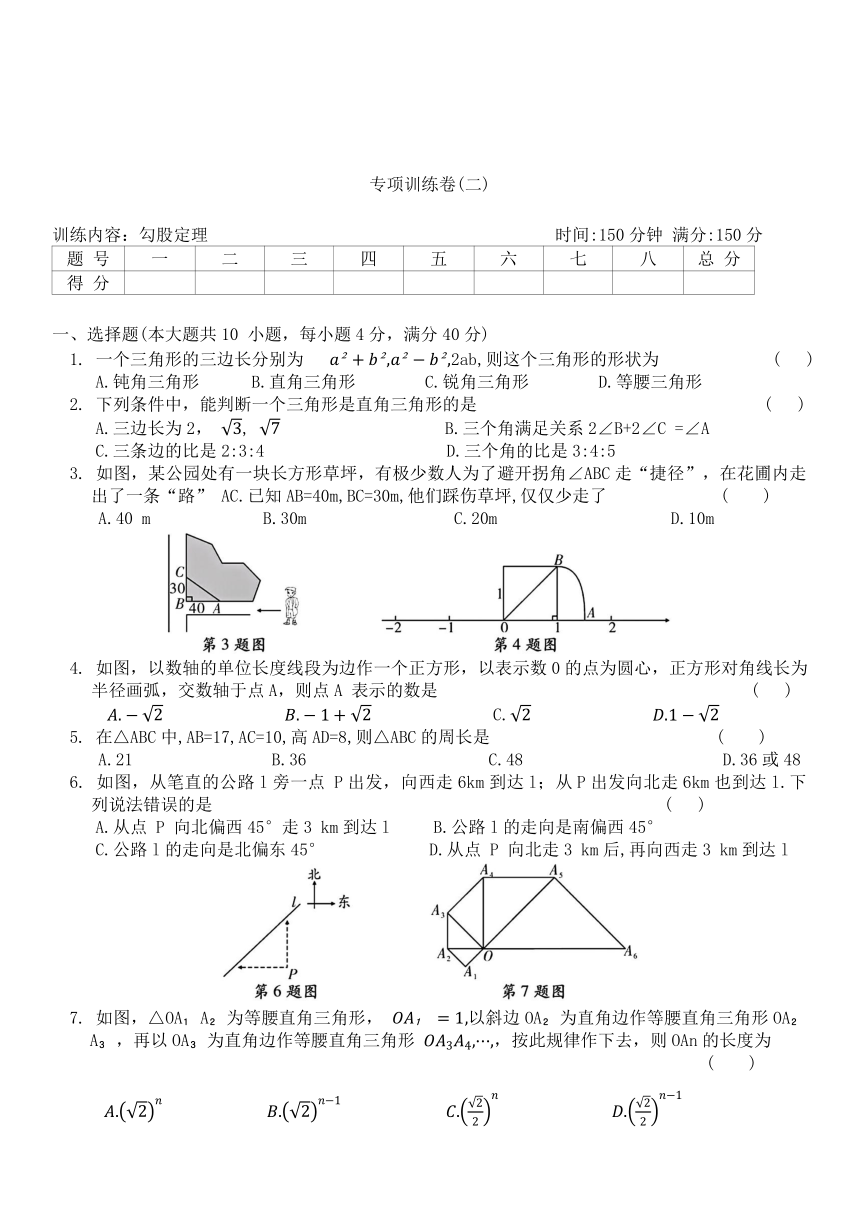
3. 如图,某公园处有一块长方形草坪,有极少数人为了避开拐角∠ABC走“捷径”,在花圃内走出了一条“路” AC.已知AB=40m,BC=30m,他们踩伤草坪,仅仅少走了 ( )
A.40 m B.30m C.20m D.10m
4. 如图,以数轴的单位长度线段为边作一个正方形,以表示数0的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A 表示的数是 ( )
C.
5. 在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是 ( )
A.21 B.36 C.48 D.36或48
6. 如图,从笔直的公路l旁一点 P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是 ( )
A.从点 P 向北偏西45°走3 km到达l B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45° D.从点 P 向北走3 km后,再向西走3 km到达l
7. 如图,△OA A 为等腰直角三角形, 以斜边OA 为直角边作等腰直角三角形OA A ,再以OA 为直角边作等腰直角三角形 ,按此规律作下去,则OAn的长度为
( )
8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
9. 如图,某小区有一块直角三角形的绿地,量得两直角边AC=6m,BC=8m,考虑到这块绿地周围还有足够多的空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC 为一直角边的直角三角形,则扩充方案共有 ( )
A.2种 B.3种 C.4种 D.5种
10. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形 EF-GH,连接EG,BD相交于点O,BD与HC相交于点 P.若GO=GP,则的值是 ( )
D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 甲、乙两人同时从同一个地点出发,甲往北偏东30°方向走了3.6公里,乙往北偏西60°方向走了4.8公里,这时甲、乙两人相距 公里.
12. 如图,在四边形ABCD中,AB=AD =4,∠A=60°,BC=4 ,CD=8,则四边形 ABCD 的面积为 .
13. 如图,每个空油桶的直径是50cm,将15个空油桶堆在一起,若要给它们盖一个遮雨棚,这个遮雨棚高至少为 cm.
14. 由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c 等于小正方形的面积( 与4个直角三角形的面积2ab的和证明了勾股定理 还可以用来证明结论:若(a>0,b>0且 为定值,则当a b时, ab取得最大值.
三、(本大题共2 小题,每小题10分,满分20分)
15. 如图,四边形 ABCD 中,∠A =∠C =90°,∠ABC=135°,CD =6,AB =2,求四边形 ABCD 的面积.
16. 勾股定理神秘而美妙,它的证法多样巧妙各有不同.当两个全等的直角三角形如图摆放时,可以用面积法来证明勾股定理,请将下面过程补充完整:
证明:连接DB,过点 D作BC边上的高DF,交 BC的延长线于点 F,
则四边形DFCE为长方形,所以 (用含字母的代数式表示)
因为
所以
所以 .
四、(本大题共2 小题,每小题10分,满分20分)
17. 已知关于x,y的方程组 与 的解相同.
(1)求a,b的值.
(2)若一个三角形的一条边的长为2 ,另外两条边的长是关于x的方程: 的解.试判断该三角形的形状,并说明理由.
18. 已知三角形的三个角 对应的边分别为a,b,c,设 记:
(1)当 时,求Q 的值.
(2)当a=b=c时,如图,设 的面积为S,求证:
五、(本题满分12分)
19. 如图,一艘船由A 港沿北偏东 方向航行10km至B港,然后再沿北偏西 方向航行10 km至C港.
(1)求A,C两港之间的距离.(结果保留到0.1km,参考数据:
(2)确定C港在A港的什么方向.
六、(本题满分12分)
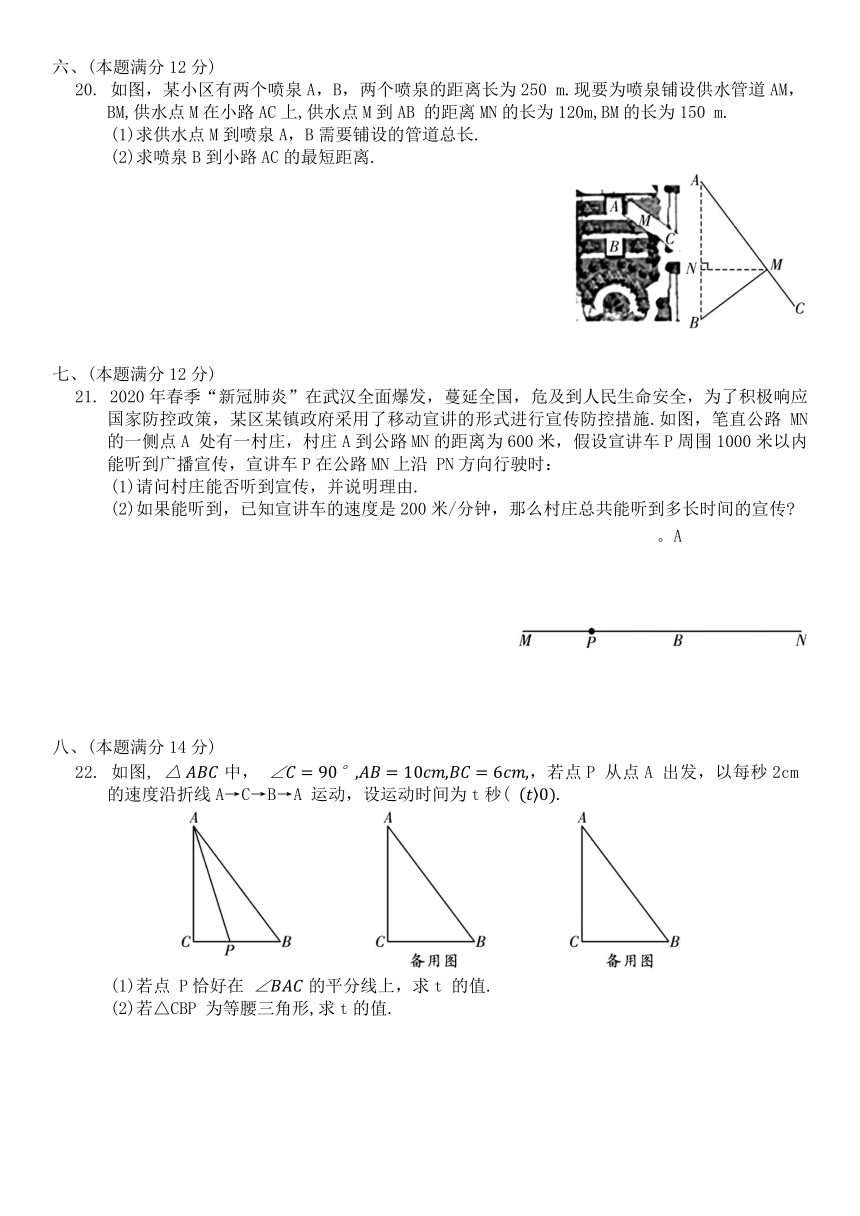
20. 如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB 的距离MN的长为120m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长.
(2)求喷泉B到小路AC的最短距离.
七、(本题满分12分)
21. 2020年春季“新冠肺炎”在武汉全面爆发,蔓延全国,危及到人民生命安全,为了积极响应国家防控政策,某区某镇政府采用了移动宣讲的形式进行宣传防控措施.如图,笔直公路 MN的一侧点A 处有一村庄,村庄A到公路MN的距离为600米,假设宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿 PN方向行驶时:
(1)请问村庄能否听到宣传,并说明理由.
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传
。A
八、(本题满分14分)
22. 如图, 中, ,若点P 从点A 出发,以每秒2cm 的速度沿折线A→C→B→A 运动,设运动时间为t秒(
(1)若点 P恰好在 的平分线上,求t 的值.
(2)若△CBP 为等腰三角形,求t的值.
专项训练卷(二)
B 2. A 3. C 4. C 5. D 6. A 7. B 8. B 9. B 10. B
11. 6 12. 4 +16 13. 50+100 14. =
15. 解:延长AB 和DC,相交于O,
在 中,根据勾股定理,得OB 在 中,根据勾股定理,得
设 则
解得
∴ 四边形ABCD 的面积
16. 证明:连接DB,过点 D作BC边上的高DF,交BC 的延长线于点 F,则四边形 DFCE 为长方形,所以, (用含字母的代数式表示)
因为
所以 所以
故答案为:
17. 解:(1)根据题意,得 解得 把 分别代入 和 解得
(2)该三角形是等腰直角三角形,理由如下:将 12代入方程 得 解得 则该三角形是等腰三角形,又∵ 该三角形是等腰直角三角形.
18. 解:(1)把( 代入 得 则
(2)证明:当 时, 为等边三角形,如图,过点A 作. 于点 D,则 在 中, 的面积
19. 解:(1)由题意,可得. 60°,∠BAN=30°,∴∠ABQ=30°,∴ ∠ABC=90°.在 中
14.1.即A,C两地之间的距离为14.1 km.
(2)由(1)知, 为等腰直角三角形, . C港在A港北偏东 的方向上.
20. 解:(1)在 中, 90(m),∴AN=AB-BN=250-90=160(m).
在 Rt△AMN中,
∴ 供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
∴ △ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM,即150 m.
21. 解:(1)村庄能听到宣传,理由如下:∵村庄A到公路MN的距离为600米,600米<1000米,∴村庄能听到宣传.
(2)如图,假设当宣讲车
行驶到P点,村庄刚能听
到宣传,行驶到 Q 点,恰
好为村庄听到宣传的最
后一刻,则 AP = AQ =
1 000 米,AB=600米,
(米),
∴PQ=1600米,
∴村庄能听到宣传的时间为:1 600÷200=8(分钟),
∴村庄总共能听到8分钟的宣传.
22. 解:(1)在△ABC中,∠C=90°,AB=10 cm,BC=6cm,
∵点P在∠BAC的平分线上,①当点 P在BC 上时,如图1,过点P作PE⊥AB于点E,∵∠C=∠AEP=90°,
∴PC=PE,
∴PB=AC+BC-2t=(14-2t) cm,PE =PC=2t-AC =(2t-8) cm.在Rt△APC和 Rt△APE 中,
在 中,由勾股定理,得 即 解得
②当点 P 运动到点A时,由题意,得 解得
综上,当点P在 的平分线上时,t的值为 或12.
(2)①如图2,当点 P 在AC 上, 时, 为等腰三角形,根据题意,得: 解得
②如图3,当点 P在AB上, 时, 为等腰三角形,根据题意,得 解得
③如图4,当点 P在AB 上,( 时, 为等腰三角形,过点C作CD⊥AB于点D, .在 中,AC 在 中, 解得
④如图5,当点 P在AB上,PC=PB时,. 为等腰三角形,过点 P作PF⊥BC于点 F,
∵PC=PB,∴CF=BF,
又∵∠ACB=∠PFB=90°,∴AC∥PF,
∴ PF为△ACB的中位线,
∴2t=AC+BC+BP=19,解得
综上所述,当△CBP为等腰三角形时,t的值为1 或10 或 或
训练内容:勾股定理 时间:150分钟 满分:150分
题 号 一 二 三 四 五 六 七 八 总 分
得 分
一、选择题(本大题共10 小题,每小题4分,满分40分)
1. 一个三角形的三边长分别为 2ab,则这个三角形的形状为 ( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.等腰三角形
2. 下列条件中,能判断一个三角形是直角三角形的是 ( )
A.三边长为2, , B.三个角满足关系2∠B+2∠C =∠A
C.三条边的比是2:3:4 D.三个角的比是3:4:5
3. 如图,某公园处有一块长方形草坪,有极少数人为了避开拐角∠ABC走“捷径”,在花圃内走出了一条“路” AC.已知AB=40m,BC=30m,他们踩伤草坪,仅仅少走了 ( )
A.40 m B.30m C.20m D.10m
4. 如图,以数轴的单位长度线段为边作一个正方形,以表示数0的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A 表示的数是 ( )
C.
5. 在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是 ( )
A.21 B.36 C.48 D.36或48
6. 如图,从笔直的公路l旁一点 P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是 ( )
A.从点 P 向北偏西45°走3 km到达l B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45° D.从点 P 向北走3 km后,再向西走3 km到达l
7. 如图,△OA A 为等腰直角三角形, 以斜边OA 为直角边作等腰直角三角形OA A ,再以OA 为直角边作等腰直角三角形 ,按此规律作下去,则OAn的长度为
( )
8. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是 ( )
A.1,4,5 B.2,3,5 C.3,4,5 D.2,2,4
9. 如图,某小区有一块直角三角形的绿地,量得两直角边AC=6m,BC=8m,考虑到这块绿地周围还有足够多的空余部分,于是打算将这块绿地扩充成等腰三角形,且扩充部分是以BC 为一直角边的直角三角形,则扩充方案共有 ( )
A.2种 B.3种 C.4种 D.5种
10. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形 EF-GH,连接EG,BD相交于点O,BD与HC相交于点 P.若GO=GP,则的值是 ( )
D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11. 甲、乙两人同时从同一个地点出发,甲往北偏东30°方向走了3.6公里,乙往北偏西60°方向走了4.8公里,这时甲、乙两人相距 公里.
12. 如图,在四边形ABCD中,AB=AD =4,∠A=60°,BC=4 ,CD=8,则四边形 ABCD 的面积为 .
13. 如图,每个空油桶的直径是50cm,将15个空油桶堆在一起,若要给它们盖一个遮雨棚,这个遮雨棚高至少为 cm.
14. 由4个直角边长分别为a,b的直角三角形围成的“赵爽弦图”如图所示,根据大正方形的面积c 等于小正方形的面积( 与4个直角三角形的面积2ab的和证明了勾股定理 还可以用来证明结论:若(a>0,b>0且 为定值,则当a b时, ab取得最大值.
三、(本大题共2 小题,每小题10分,满分20分)
15. 如图,四边形 ABCD 中,∠A =∠C =90°,∠ABC=135°,CD =6,AB =2,求四边形 ABCD 的面积.
16. 勾股定理神秘而美妙,它的证法多样巧妙各有不同.当两个全等的直角三角形如图摆放时,可以用面积法来证明勾股定理,请将下面过程补充完整:
证明:连接DB,过点 D作BC边上的高DF,交 BC的延长线于点 F,
则四边形DFCE为长方形,所以 (用含字母的代数式表示)
因为
所以
所以 .
四、(本大题共2 小题,每小题10分,满分20分)
17. 已知关于x,y的方程组 与 的解相同.
(1)求a,b的值.
(2)若一个三角形的一条边的长为2 ,另外两条边的长是关于x的方程: 的解.试判断该三角形的形状,并说明理由.
18. 已知三角形的三个角 对应的边分别为a,b,c,设 记:
(1)当 时,求Q 的值.
(2)当a=b=c时,如图,设 的面积为S,求证:
五、(本题满分12分)
19. 如图,一艘船由A 港沿北偏东 方向航行10km至B港,然后再沿北偏西 方向航行10 km至C港.
(1)求A,C两港之间的距离.(结果保留到0.1km,参考数据:
(2)确定C港在A港的什么方向.
六、(本题满分12分)
20. 如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB 的距离MN的长为120m,BM的长为150 m.
(1)求供水点M到喷泉A,B需要铺设的管道总长.
(2)求喷泉B到小路AC的最短距离.
七、(本题满分12分)
21. 2020年春季“新冠肺炎”在武汉全面爆发,蔓延全国,危及到人民生命安全,为了积极响应国家防控政策,某区某镇政府采用了移动宣讲的形式进行宣传防控措施.如图,笔直公路 MN的一侧点A 处有一村庄,村庄A到公路MN的距离为600米,假设宣讲车P周围1000米以内能听到广播宣传,宣讲车P在公路MN上沿 PN方向行驶时:
(1)请问村庄能否听到宣传,并说明理由.
(2)如果能听到,已知宣讲车的速度是200米/分钟,那么村庄总共能听到多长时间的宣传
。A
八、(本题满分14分)
22. 如图, 中, ,若点P 从点A 出发,以每秒2cm 的速度沿折线A→C→B→A 运动,设运动时间为t秒(
(1)若点 P恰好在 的平分线上,求t 的值.
(2)若△CBP 为等腰三角形,求t的值.
专项训练卷(二)
B 2. A 3. C 4. C 5. D 6. A 7. B 8. B 9. B 10. B
11. 6 12. 4 +16 13. 50+100 14. =
15. 解:延长AB 和DC,相交于O,
在 中,根据勾股定理,得OB 在 中,根据勾股定理,得
设 则
解得
∴ 四边形ABCD 的面积
16. 证明:连接DB,过点 D作BC边上的高DF,交BC 的延长线于点 F,则四边形 DFCE 为长方形,所以, (用含字母的代数式表示)
因为
所以 所以
故答案为:
17. 解:(1)根据题意,得 解得 把 分别代入 和 解得
(2)该三角形是等腰直角三角形,理由如下:将 12代入方程 得 解得 则该三角形是等腰三角形,又∵ 该三角形是等腰直角三角形.
18. 解:(1)把( 代入 得 则
(2)证明:当 时, 为等边三角形,如图,过点A 作. 于点 D,则 在 中, 的面积
19. 解:(1)由题意,可得. 60°,∠BAN=30°,∴∠ABQ=30°,∴ ∠ABC=90°.在 中
14.1.即A,C两地之间的距离为14.1 km.
(2)由(1)知, 为等腰直角三角形, . C港在A港北偏东 的方向上.
20. 解:(1)在 中, 90(m),∴AN=AB-BN=250-90=160(m).
在 Rt△AMN中,
∴ 供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
∴ △ABM是直角三角形,∴BM⊥AC,
∴喷泉B到小路AC的最短距离是BM,即150 m.
21. 解:(1)村庄能听到宣传,理由如下:∵村庄A到公路MN的距离为600米,600米<1000米,∴村庄能听到宣传.
(2)如图,假设当宣讲车
行驶到P点,村庄刚能听
到宣传,行驶到 Q 点,恰
好为村庄听到宣传的最
后一刻,则 AP = AQ =
1 000 米,AB=600米,
(米),
∴PQ=1600米,
∴村庄能听到宣传的时间为:1 600÷200=8(分钟),
∴村庄总共能听到8分钟的宣传.
22. 解:(1)在△ABC中,∠C=90°,AB=10 cm,BC=6cm,
∵点P在∠BAC的平分线上,①当点 P在BC 上时,如图1,过点P作PE⊥AB于点E,∵∠C=∠AEP=90°,
∴PC=PE,
∴PB=AC+BC-2t=(14-2t) cm,PE =PC=2t-AC =(2t-8) cm.在Rt△APC和 Rt△APE 中,
在 中,由勾股定理,得 即 解得
②当点 P 运动到点A时,由题意,得 解得
综上,当点P在 的平分线上时,t的值为 或12.
(2)①如图2,当点 P 在AC 上, 时, 为等腰三角形,根据题意,得: 解得
②如图3,当点 P在AB上, 时, 为等腰三角形,根据题意,得 解得
③如图4,当点 P在AB 上,( 时, 为等腰三角形,过点C作CD⊥AB于点D, .在 中,AC 在 中, 解得
④如图5,当点 P在AB上,PC=PB时,. 为等腰三角形,过点 P作PF⊥BC于点 F,
∵PC=PB,∴CF=BF,
又∵∠ACB=∠PFB=90°,∴AC∥PF,
∴ PF为△ACB的中位线,
∴2t=AC+BC+BP=19,解得
综上所述,当△CBP为等腰三角形时,t的值为1 或10 或 或
