物理人教版(2019)选择性必修第一册4.1光的折射(共34张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册4.1光的折射(共34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 66.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-12 13:45:46 | ||
图片预览




文档简介
(共34张PPT)
第四单元 《光》
4.1 光的折射
一、驱动问题
“万华镜旋之空”是一种罕见的大气现象,堪称冰晕中的极品。
2022年,新疆博尔塔拉蒙古自治州境内的赛里木湖景区出现了罕见冰晕奇观,多种冰晕如万花筒般交织在空中,复杂的虹、幻日、光晕同时出现,持续了近一个半小时。
这种如万花筒般交织在空中复杂的虹、幻日、光晕同时出现壮观又神奇。
冰晕本身就不可预测,转瞬即逝,这种组合冰晕更是可遇不可求。你知道它的形成原因吗?
点击播放视频
一、驱动问题
点击播放视频
万华镜旋之空
二、光的反射
界面
入射光线
反射光线
法线
入射角
反射角
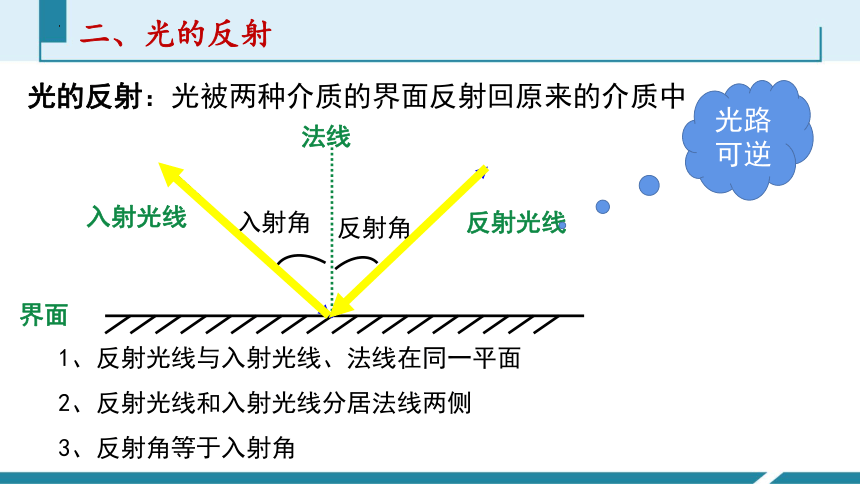
光的反射:光被两种介质的界面反射回原来的介质中
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
光路可逆
二、光的发射
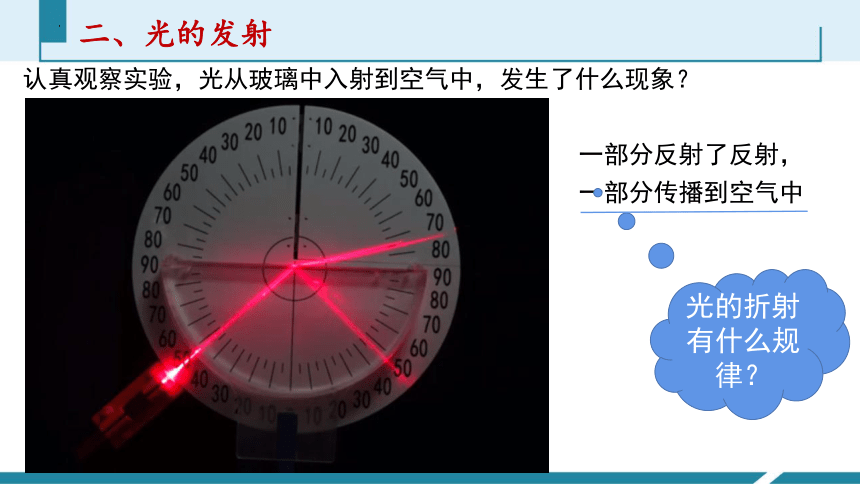
认真观察实验,光从玻璃中入射到空气中,发生了什么现象?
一部分反射了反射,
一部分传播到空气中
光的折射有什么规律?
三、光的折射
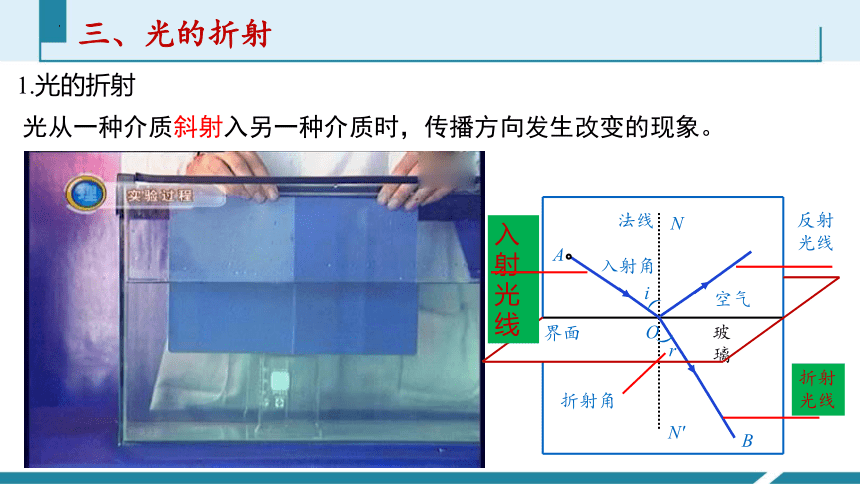
1.光的折射
光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
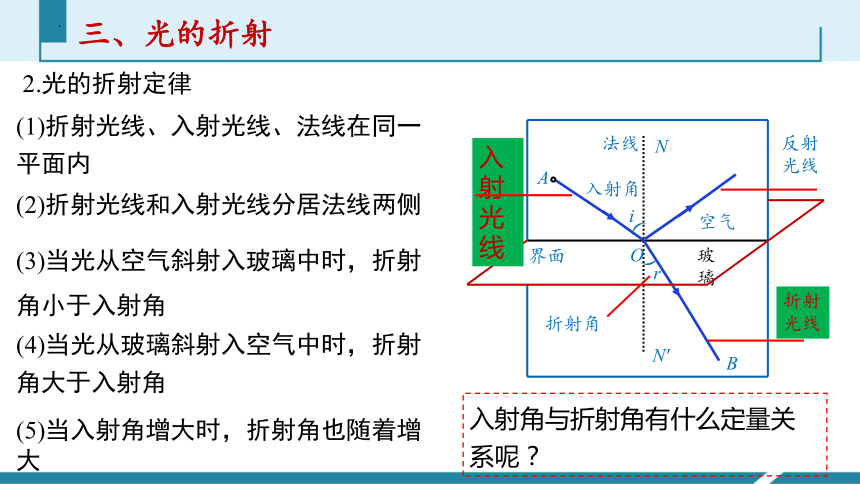
(1)折射光线、入射光线、法线在同一平面内
(2)折射光线和入射光线分居法线两侧
(3)当光从空气斜射入玻璃中时,折射角小于入射角
(4)当光从玻璃斜射入空气中时,折射角大于入射角
(5)当入射角增大时,折射角也随着增大
2.光的折射定律
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
入射角与折射角有什么定量关系呢?
三、光的折射
三、光的折射
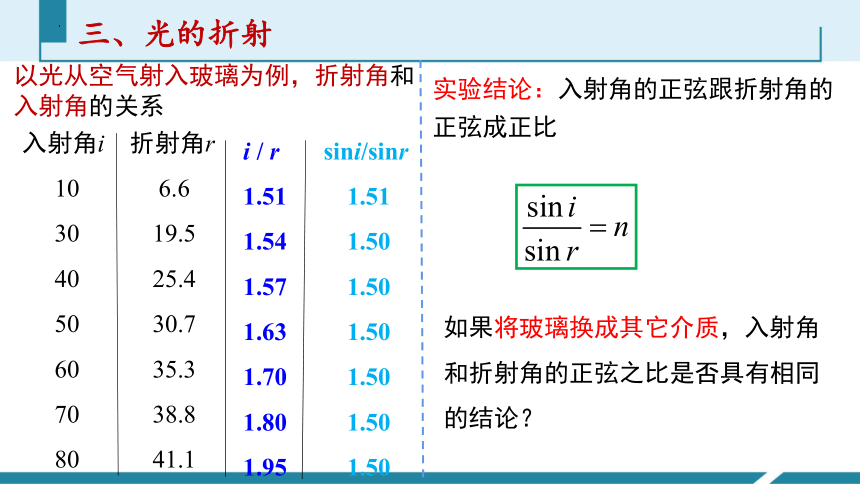
以光从空气射入玻璃为例,折射角和入射角的关系
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
实验结论:入射角的正弦跟折射角的正弦成正比
如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
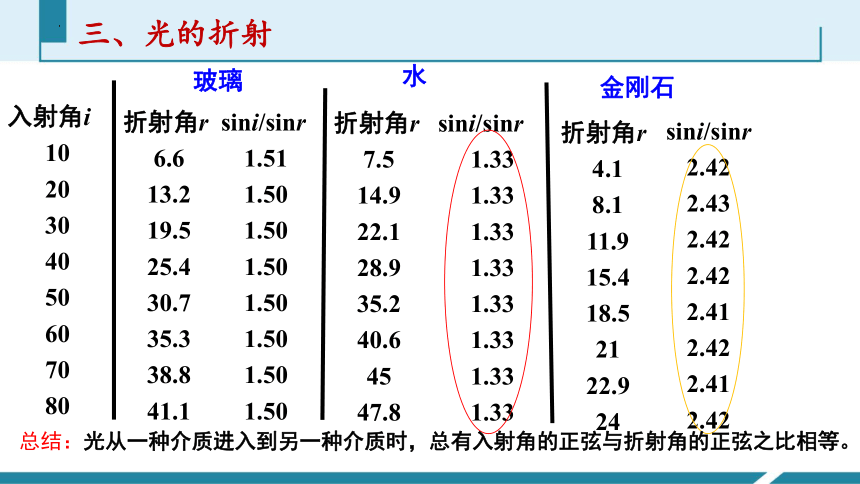
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
三、光的折射
三、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
三、光的折射
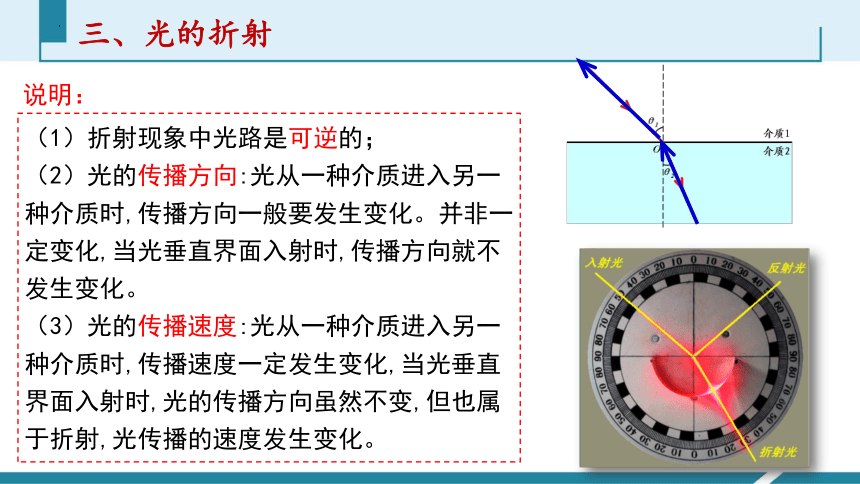
说明:
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
点击播放视频
四、折射率
发生海市蜃楼的条件是什么?
四、折射率
(一)思考与讨论
你还能发现什么规律?
常数与介质有关系,是一个反映介质的光学性质的物理量。常数越大,光线以相同入射角从真空斜射入这种介质时偏折的角度越大。
四、折射率
(二)折射率
说明:(1)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(2)折射率无单位,任何介质的折射率皆大于1。
2.定义式:
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
四、折射率
说明:(4)光从一种介质进入另一种介质时,折射角与入射角的大小关系不要一概而论,要视两种介质的折射率大小而定。
(5)当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
(二)折射率
典例选讲:
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶低上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
解:
方法分析:
解决光的反射、折射问题的方法:
五、实验:测定玻璃的折射率
(一)实验思路
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
思路:选取一块玻璃砖按在白纸上,作出玻璃砖的轮廓,然后作出入射玻璃砖的光线和出射玻璃砖的光线,最后连接入射点和出射点的光线,这就是折射光线。最后测出入射角和折射角的大小,代入公式就可以得出答案。
五、实验:测定玻璃的折射率
(一)实验思路:
如何作出入射光线和出射光线?
在白纸上画一条直线aa′,并取aa′上的一点O为入射点,作过O的法线NN′,画出线段AO作为入射光线,并在AO上插上P1、P2两根大头针,在白纸上放上玻璃砖,使玻璃砖的一条长边与直线aa′对齐,并画出另一条长边的对齐线bb′,再在另一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3、P2、P1的像,记下P3、P4位置;
五、实验:测定玻璃的折射率
(二)实验方案
请设计出实验方案,并与其他同学交流?
五、实验:测定玻璃的折射率
(三)数据分析
如何进行数据分析才能得出结论?
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图1所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
五、实验:测定玻璃的折射率
(三)数据分析
如何进行数据分析才能得出结论?
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 , ,且CO=DO,所以折射率 。
五、实验:测定玻璃的折射率
(四)注意事项
做该实验时需要注意什么事项?
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
五、实验:测定玻璃的折射率
(四)注意事项
哪些原因会导致实验有误差?
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
课堂小结
光的折射
折射定律:
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比:
折射率
公式:
测定玻璃的折射率
实验:
定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
课堂反馈
B
课堂反馈
课堂反馈
D
课堂反馈
课堂反馈
C
课堂反馈
课堂反馈
4.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最小
D.光在介质C中的速度最大
B
课堂反馈
本课时结束
感谢观看!
第四单元 《光》
4.1 光的折射
一、驱动问题
“万华镜旋之空”是一种罕见的大气现象,堪称冰晕中的极品。
2022年,新疆博尔塔拉蒙古自治州境内的赛里木湖景区出现了罕见冰晕奇观,多种冰晕如万花筒般交织在空中,复杂的虹、幻日、光晕同时出现,持续了近一个半小时。
这种如万花筒般交织在空中复杂的虹、幻日、光晕同时出现壮观又神奇。
冰晕本身就不可预测,转瞬即逝,这种组合冰晕更是可遇不可求。你知道它的形成原因吗?
点击播放视频
一、驱动问题
点击播放视频
万华镜旋之空
二、光的反射
界面
入射光线
反射光线
法线
入射角
反射角
光的反射:光被两种介质的界面反射回原来的介质中
1、反射光线与入射光线、法线在同一平面
2、反射光线和入射光线分居法线两侧
3、反射角等于入射角
光路可逆
二、光的发射
认真观察实验,光从玻璃中入射到空气中,发生了什么现象?
一部分反射了反射,
一部分传播到空气中
光的折射有什么规律?
三、光的折射
1.光的折射
光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
(1)折射光线、入射光线、法线在同一平面内
(2)折射光线和入射光线分居法线两侧
(3)当光从空气斜射入玻璃中时,折射角小于入射角
(4)当光从玻璃斜射入空气中时,折射角大于入射角
(5)当入射角增大时,折射角也随着增大
2.光的折射定律
N
N′
空气
玻璃
i
r
O
A
B
界面
法线
入射光线
折射光线
入射角
折射角
(
(
反射光线
入射角与折射角有什么定量关系呢?
三、光的折射
三、光的折射
以光从空气射入玻璃为例,折射角和入射角的关系
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
实验结论:入射角的正弦跟折射角的正弦成正比
如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
三、光的折射
三、光的折射
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者之间的关系,并把它总结为光的折射定律。
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
三、光的折射
说明:
(1)折射现象中光路是可逆的;
(2)光的传播方向:光从一种介质进入另一种介质时,传播方向一般要发生变化。并非一定变化,当光垂直界面入射时,传播方向就不发生变化。
(3)光的传播速度:光从一种介质进入另一种介质时,传播速度一定发生变化,当光垂直界面入射时,光的传播方向虽然不变,但也属于折射,光传播的速度发生变化。
点击播放视频
四、折射率
发生海市蜃楼的条件是什么?
四、折射率
(一)思考与讨论
你还能发现什么规律?
常数与介质有关系,是一个反映介质的光学性质的物理量。常数越大,光线以相同入射角从真空斜射入这种介质时偏折的角度越大。
四、折射率
(二)折射率
说明:(1)n的大小与θ1和θ2无关,与介质和入射光的频率有关,对于确定的介质,n是定值,不能说n∝sinθ1或n∝1/sinθ2
(2)折射率无单位,任何介质的折射率皆大于1。
2.定义式:
(3)折射率反映介质对光的偏折作用,n越大光线偏折越厉害。
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
四、折射率
说明:(4)光从一种介质进入另一种介质时,折射角与入射角的大小关系不要一概而论,要视两种介质的折射率大小而定。
(5)当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
(二)折射率
典例选讲:
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶低上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
解:
方法分析:
解决光的反射、折射问题的方法:
五、实验:测定玻璃的折射率
(一)实验思路
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
思路:选取一块玻璃砖按在白纸上,作出玻璃砖的轮廓,然后作出入射玻璃砖的光线和出射玻璃砖的光线,最后连接入射点和出射点的光线,这就是折射光线。最后测出入射角和折射角的大小,代入公式就可以得出答案。
五、实验:测定玻璃的折射率
(一)实验思路:
如何作出入射光线和出射光线?
在白纸上画一条直线aa′,并取aa′上的一点O为入射点,作过O的法线NN′,画出线段AO作为入射光线,并在AO上插上P1、P2两根大头针,在白纸上放上玻璃砖,使玻璃砖的一条长边与直线aa′对齐,并画出另一条长边的对齐线bb′,再在另一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3、P2、P1的像,记下P3、P4位置;
五、实验:测定玻璃的折射率
(二)实验方案
请设计出实验方案,并与其他同学交流?
五、实验:测定玻璃的折射率
(三)数据分析
如何进行数据分析才能得出结论?
1.平均值法
算出不同入射角时的比值 ,最后求出在几次实验中所测的 平均值,即为玻璃砖的折射率。
2.图象法
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图1所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
五、实验:测定玻璃的折射率
(三)数据分析
如何进行数据分析才能得出结论?
3.作图法
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 , ,且CO=DO,所以折射率 。
五、实验:测定玻璃的折射率
(四)注意事项
做该实验时需要注意什么事项?
(1)实验时,尽可能将大头针竖直插在纸上,且P1和P2之间,P2与O点之间,P3与P4之间,P3与O′点之间距离要稍大一些。
(2)入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大,也不宜太小。
(3)在操作时,手不能触摸玻璃砖的光洁面。更不能把玻璃砖界面当尺子画界线。
(4)在实验过程中,玻璃砖与白纸的相对位置不能改变。
(5)玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
五、实验:测定玻璃的折射率
(四)注意事项
哪些原因会导致实验有误差?
(1)入射光线和出射光线确定得不够精确,因此要求插大头针时,两大头针间距应适当大一些。
(2)入射角和折射角的测量造成误差,故入射角应适当大些,以减小测量的相对误差。
课堂小结
光的折射
折射定律:
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比:
折射率
公式:
测定玻璃的折射率
实验:
定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。用符号 n 表示。
课堂反馈
B
课堂反馈
课堂反馈
D
课堂反馈
课堂反馈
C
课堂反馈
课堂反馈
4.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最小
D.光在介质C中的速度最大
B
课堂反馈
本课时结束
感谢观看!
