实数-平方根课件
图片预览





文档简介
课件16张PPT。
平方根
学习目标:
(1)了解平方根的概念;掌握平方根的特征.
(2)能利用开平方与平方互为逆运算的关系,
求某些非负数的平方根.
学习重点:
平方根的概念.课件说明(1)什么是算术平方根?怎样表示?如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.a的算术平方根表示为:0的算术平方根是0负数没有算术平方根(2)256的算术平方根是 ,5的算
术平方根是 .(3)下列各式有意义的条件是什么?16(4) ①一块正方形菜地的边长是3米,这块菜地的面积是多少平方米?
②已知一块正方形菜地的面积是9平方米,求它的边长.
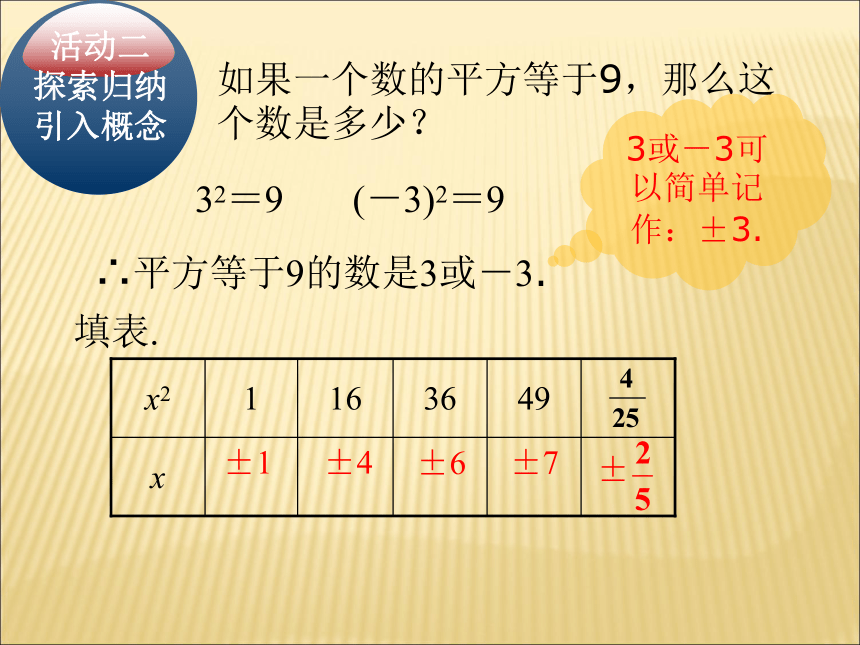
③如果一个数的平方等于9,这个数是多少?93x=3或 x= -3如果一个数的平方等于9,那么这个数是多少?32=9(-3)2=9∴平方等于9的数是3或-3.3或-3可以简单记作:±3.±1±4±6±7± 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.平方根定义例如:3和-3是9的平方根,简记为±3是9的平方根.
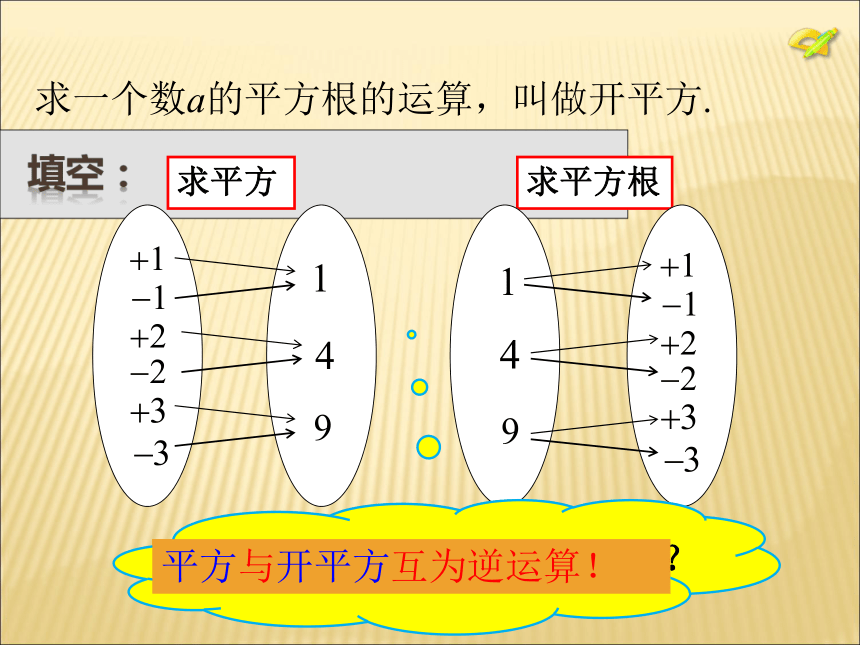
填空:求平方求平方根
平方与开平方互为逆运算!求一个数a的平方根的运算,叫做开平方.例4. 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1) ∵(±10)2=100,
∴100的平方根是±10;(3) ∵(±0.5)2=0.25,
∴0.25的平方根是±0.5. (2) ∵(± )2= ,
∴ 的平方根是± ;1.一个正数有几个平方根?
它们有什么特点?
2.0有几个平方根?是多少?
3.负数呢?1.正数的平方根有两个,它们互为相反数.3.负数没有平方根.2.0有一个平方根,它是0本身.平方根的性质正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.读作 “正、负根号a”25的平方根是±5,用符号语言表达为:正数a的算术平方根正数a的算术平方根的相反数(即正数a的负的平方根)正数a的平方根例如:9的平方根是±3,用符号语言表达为:平方根的表示方法1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0正数a的算术平方根有一个
正数a的平方根有两个
如果一个正数x的平方等于a,那么这个正数就叫做a的算术平方根
如果一个数的平方等于a,这个数就叫做a的平方根
符号不同个数不同定义不同用 表示
用 表示平方根与算术平方根的比较例5. 求下列各式的值.解:(1) ∵ 62=36,∴ =6;(2) ∵ 0.92=0.81, ∴- =-0.9;(3) ∵( )2= , ∴ ± =± .36的算术平方根0.81的负的平方根的平方根√√XX4.计算下列各式的值:3.如果一个正数的平方根是a-1和a+3,则a=____,这个正数是__.4-1本节课你学习了哪些知识?在探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?课堂小结解下列方程:
(1)4x2=9;(2)x2-81=0;(3)(x+1)2=1.拓展延伸:
平方根
学习目标:
(1)了解平方根的概念;掌握平方根的特征.
(2)能利用开平方与平方互为逆运算的关系,
求某些非负数的平方根.
学习重点:
平方根的概念.课件说明(1)什么是算术平方根?怎样表示?如果一个正数x的平方等于a,那么这个正数x叫做a的算术平方根.a的算术平方根表示为:0的算术平方根是0负数没有算术平方根(2)256的算术平方根是 ,5的算
术平方根是 .(3)下列各式有意义的条件是什么?16(4) ①一块正方形菜地的边长是3米,这块菜地的面积是多少平方米?
②已知一块正方形菜地的面积是9平方米,求它的边长.
③如果一个数的平方等于9,这个数是多少?93x=3或 x= -3如果一个数的平方等于9,那么这个数是多少?32=9(-3)2=9∴平方等于9的数是3或-3.3或-3可以简单记作:±3.±1±4±6±7± 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.平方根定义例如:3和-3是9的平方根,简记为±3是9的平方根.
填空:求平方求平方根
平方与开平方互为逆运算!求一个数a的平方根的运算,叫做开平方.例4. 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1) ∵(±10)2=100,
∴100的平方根是±10;(3) ∵(±0.5)2=0.25,
∴0.25的平方根是±0.5. (2) ∵(± )2= ,
∴ 的平方根是± ;1.一个正数有几个平方根?
它们有什么特点?
2.0有几个平方根?是多少?
3.负数呢?1.正数的平方根有两个,它们互为相反数.3.负数没有平方根.2.0有一个平方根,它是0本身.平方根的性质正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.读作 “正、负根号a”25的平方根是±5,用符号语言表达为:正数a的算术平方根正数a的算术平方根的相反数(即正数a的负的平方根)正数a的平方根例如:9的平方根是±3,用符号语言表达为:平方根的表示方法1.平方根包括算术平方根,算术平方根是平方根中非负的那一个.
2.存在条件相同.只有非负数才有平方根和算术平方根.
3.0的平方根和算术平方根均为0正数a的算术平方根有一个
正数a的平方根有两个
如果一个正数x的平方等于a,那么这个正数就叫做a的算术平方根
如果一个数的平方等于a,这个数就叫做a的平方根
符号不同个数不同定义不同用 表示
用 表示平方根与算术平方根的比较例5. 求下列各式的值.解:(1) ∵ 62=36,∴ =6;(2) ∵ 0.92=0.81, ∴- =-0.9;(3) ∵( )2= , ∴ ± =± .36的算术平方根0.81的负的平方根的平方根√√XX4.计算下列各式的值:3.如果一个正数的平方根是a-1和a+3,则a=____,这个正数是__.4-1本节课你学习了哪些知识?在探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?课堂小结解下列方程:
(1)4x2=9;(2)x2-81=0;(3)(x+1)2=1.拓展延伸:
