八年级数学上册新苏科版2015-2016学年期末复习讲义:第1章《全等三角形》教案
文档属性
| 名称 | 八年级数学上册新苏科版2015-2016学年期末复习讲义:第1章《全等三角形》教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 103.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-04 00:00:00 | ||
图片预览


文档简介
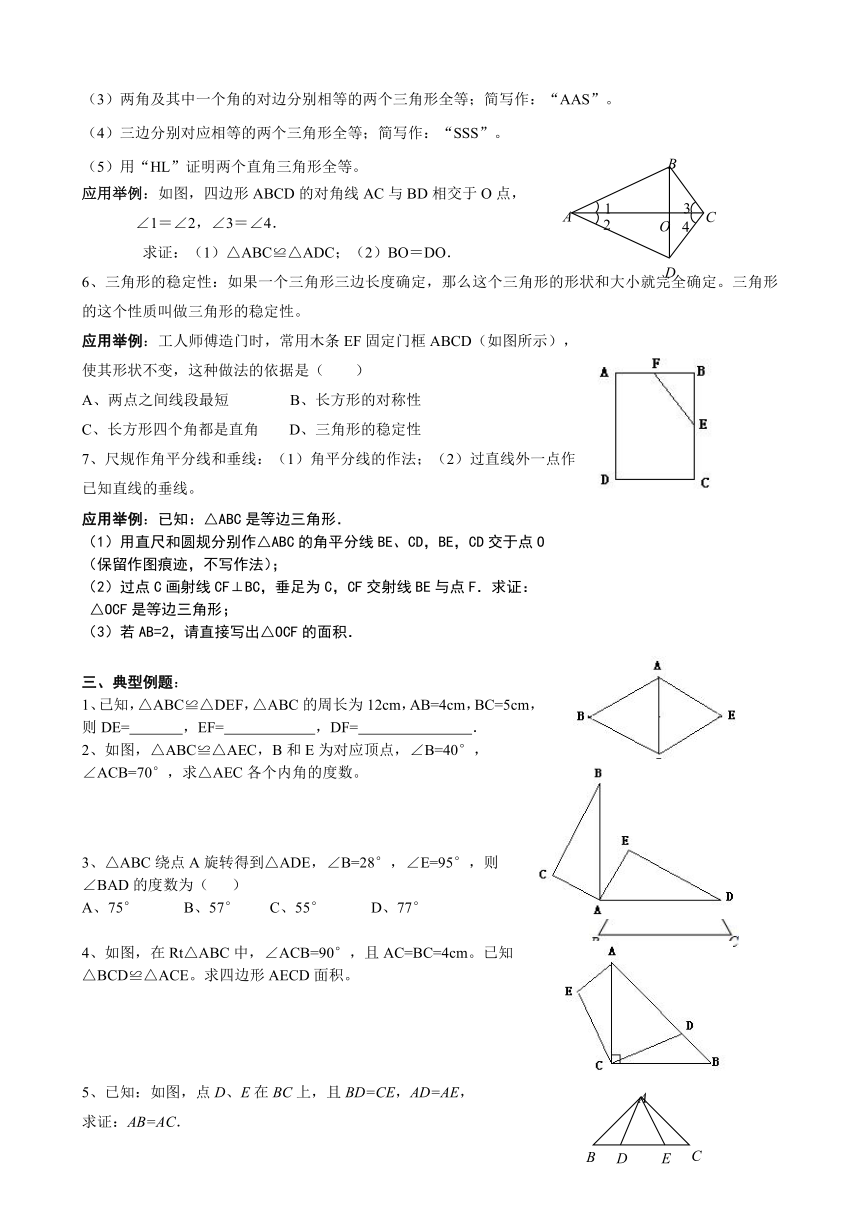
2015-16学年第一学期苏科版初二数学《全等三角形》复习讲义
一、知识系统:
二、知识点:
1、定义:能够完全重合的图形叫做全等图形。
(1)“完全重合”是指两个图形的形状相同、大小相等;
(2)全等图形是指两个或两个以上的图形之间的关系。一个图形不能称为全等图形。
特征:(1)形状相同;(2)大小相等。
应用举例:(1)下列四个图形是全等图形的是( )
( http: / / www.21cnjy.com )
(2)如图,中有6个条形方格图,图上由实线围成的图形是全等形的有哪几对_____.
2、全等图形作法及分割:
(1)全等图形的作法:依据图形的平移、翻 ( http: / / www.21cnjy.com )折、旋转三种基本变换,作图的关键是先找出关键点,然后确定关键点经过变换后的位置,最后确定图形的位置。
(2)全等图形的分割:把一个图形分割成两个 ( http: / / www.21cnjy.com )或几个全等图形,一般的分割思路有:(1)利用中心对称图形性质分割图形;(2)利用图形在分割前后面积不变寻求分割方法。
(3)利用全等图形设计图案:先把图形割补,在设计图案,最后无缝拼接。
3、全等三角形的定义及表示(重点)
两个能够完全重合的三角形叫做全等三角形。
如图所示:
△ABC与△DEF是全等三角形,记作
△ABC≌△DEF。其中(1)顶点A和D、B和E、C和F叫做对应顶点;
(2)AB和DE、BC和EF、AC和DF是对应边;
(3)∠A和∠D、∠B和∠E、∠C和∠F叫做对应角。
说明:把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
(4)找对应边、对应角的常用方法:
全等三角形的对应角所对的边是对应边,两个对应角所夹的边是对应边;
全等三角形的对应边所对的角是对应角,两条对应边所夹的角是对应角;
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
全等三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
应用举例:如图,△ABC≌△ABD,图中有相等的角吗?有相等的边吗?请找出来,并说明你的理由.
4、全等三角形的性质:
全等三角形的对应边相等;对应角相等。
几何语言:如果△ABC≌△DEF,则∠A=∠D,∠B=∠E,∠C=∠F,AB=DE,AC=DF,BC=EF。
注意:(1)两个三角形全等是对应边和对应角相等的前提。如果没有全等三角形,就没有对应边相等,对应角相等。
(2)利用全等三角形的性质解题时,一定要注意“对应”二字,在用字母表示时,也要对应着写,两个对应角所对的边一定是对应边。
(3)两个三角形全等,就是两个三角形能够完 ( http: / / www.21cnjy.com )全重合。所以不仅对应边相等,对应角相等,对应角平分线、对应高线和对应中线也相等,而且它们的周长和面积也相等。
(4)三角形全等具有传递性。
5、三角形全等的判定条件:(重点)
(1)两边及其夹角分别对应相等的两个三角形全等;简写作:“SAS”。
(2)两角及其夹边分别对应相等的两个三角形全等;简写作:“ASA”。
(3)两角及其中一个角的对边分别相等的两个三角形全等;简写作:“AAS”。
(4)三边分别对应相等的两个三角形全等;简写作:“SSS”。
(5)用“HL”证明两个直角三角形全等。
应用举例:如图,四边形ABCD的对角线AC与BD相交于O点,
∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;(2)BO=DO.
6、三角形的稳定性:如果一个三角形三边长度确定,那么这个三角形的形状和大小就完全确定。三角形的这个性质叫做三角形的稳定性。
应用举例:工人师傅造门时,常用木条EF固定门框ABCD(如图所示),使其形状不变,这种做法的依据是( )
A、两点之间线段最短 B、长方形的对称性
C、长方形四个角都是直角 D、三角形的稳定性
7、尺规作角平分线和垂线:(1)角平分线的作法;(2)过直线外一点作已知直线的垂线。
应用举例:已知:△ABC是等边三角形.
(1)用直尺和圆规分别作△ABC的角平分线BE、CD,BE,CD交于点O
(保留作图痕迹,不写作法);
(2)过点C画射线CF⊥BC,垂足为C,CF交射线BE与点F.求证:
△OCF是等边三角形;
(3)若AB=2,请直接写出△OCF的面积.
三、典型例题:
1、已知,△ABC≌△DE ( http: / / www.21cnjy.com )F,△ABC的周长为12cm,AB=4cm,BC=5cm,则DE= ,EF= ,DF= .
2、如图,△ABC≌△AEC,B和E为对应顶点,∠B=40°,
∠ACB=70°,求△AEC各个内角的度数。
3、△ABC绕点A旋转得到△ADE,∠B=28°,∠E=95°,则
∠BAD的度数为( )
A、75° B、57° C、55° D、77°
4、如图,在Rt△ABC中,∠ACB=90°,且AC=BC=4cm。已知
△BCD≌△ACE。求四边形AECD面积。
5、已知:如图,点D、E在BC上,且BD=CE,AD=AE,
求证:AB=AC.
6、已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
7、已知:BE⊥CD,BE=DE,BC=DA,
求证:①△BEC≌△DEA;
②DF⊥BC.
8、如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,
BC、DE交于点O.
求证:(1) △ABC≌△AED; (2) OB=OE
说明:证明两个三角形全等时图形中常用的隐含条件:
判定两个三角形全等,寻找条件时,应该注 ( http: / / www.21cnjy.com )意图形中的隐含条件,常见的有:(1)公共边或公共角相等;(2)对顶角相等;(3)等边加(或减)等边,其和(或其差)仍相等;(4)等角加(或减)等角,其和(或差)仍相等;(5)同角或等角的余角(或补角)相等;(6)有中线或角平分线的定义得出线段或角相等;(7)由垂直定义得出直角相等。另外,一些自然规律如:“太阳光线可以看成是平行的”,“光的反射角等于入射角”等也是常用的隐含条件。
四、基础训练:
1、如图,已知AB=AD,要使△ABC≌△ADC,可增加条件 ,
理由是 定理。
2、下列说法中正确的是( )
A、两个直角三角形全等 B、两个等腰三角形全等
C、两个等边三角形全等 D、两条直角边对应相等的直角三角形全等
3、如图,△ABC中,∠C=90 ,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,
且CD=6cm,则DE的长为( )
A、4cm B、6cm C、8cm D、10cm
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
4、三角形内到三条边的距离相等的点是( )
A、三角形的三条角平分线的交点 B、三角形的三条高的交点
C、三角形的三条中线的交点 D、三角形的三边的垂直平分线的交点
5、三角形内到三个顶点的距离相等的点是( )
A、三角形的三条角平分线的交点 B、三角形的三条高的交点
C、三角形的三条中线的交点 D、三角形的三边的垂直平分线的交点
6、在△ABC中,∠A=70 ,∠B=40 ,则△ABC是( )
A、钝角三角形 B、等腰三角形 C、等边三角形
D、等腰直角三角形
7、如图,AE=BE,∠C=∠D,求证:△ABC≌△BAD。
8、如图,在△ABC和△DEF中, ( http: / / www.21cnjy.com )B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
①AB=DE, ②AC=DF, ③∠ABC=∠DEF, ④BE=CF.
解:我写的真命题是:
在△ABC和△DEF中,
如果 ,
那么 。(不能只填序号)
证明如下:
9、已知:AC ,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等?
10、如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD(SSS)
11、如图,点E、F在AB上,且AF=BE,AC=BD,AC∥BD.求证:CF∥DE
12、如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)求证: △BCE≌△CAD;
(2)猜想:AD,DE,BE的数量关系为 (不需证明);
(3)当CE绕点C旋转到图2位置时,猜想线段AD,DE,BE之间又有怎样的数量关系,并证明你的结论.
D
C
B
A
O
1
2
3
4
A
B
C
D
E
B
C
D
E
F
A
B
C
D
E
F
A
E
B
D
A
图2
C
B
E
C
D
A
一、知识系统:
二、知识点:
1、定义:能够完全重合的图形叫做全等图形。
(1)“完全重合”是指两个图形的形状相同、大小相等;
(2)全等图形是指两个或两个以上的图形之间的关系。一个图形不能称为全等图形。
特征:(1)形状相同;(2)大小相等。
应用举例:(1)下列四个图形是全等图形的是( )
( http: / / www.21cnjy.com )
(2)如图,中有6个条形方格图,图上由实线围成的图形是全等形的有哪几对_____.
2、全等图形作法及分割:
(1)全等图形的作法:依据图形的平移、翻 ( http: / / www.21cnjy.com )折、旋转三种基本变换,作图的关键是先找出关键点,然后确定关键点经过变换后的位置,最后确定图形的位置。
(2)全等图形的分割:把一个图形分割成两个 ( http: / / www.21cnjy.com )或几个全等图形,一般的分割思路有:(1)利用中心对称图形性质分割图形;(2)利用图形在分割前后面积不变寻求分割方法。
(3)利用全等图形设计图案:先把图形割补,在设计图案,最后无缝拼接。
3、全等三角形的定义及表示(重点)
两个能够完全重合的三角形叫做全等三角形。
如图所示:
△ABC与△DEF是全等三角形,记作
△ABC≌△DEF。其中(1)顶点A和D、B和E、C和F叫做对应顶点;
(2)AB和DE、BC和EF、AC和DF是对应边;
(3)∠A和∠D、∠B和∠E、∠C和∠F叫做对应角。
说明:把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
(4)找对应边、对应角的常用方法:
全等三角形的对应角所对的边是对应边,两个对应角所夹的边是对应边;
全等三角形的对应边所对的角是对应角,两条对应边所夹的角是对应角;
有公共边的,公共边是对应边;
有公共角的,公共角是对应角;
有对顶角的,对顶角是对应角;
全等三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角)。
应用举例:如图,△ABC≌△ABD,图中有相等的角吗?有相等的边吗?请找出来,并说明你的理由.
4、全等三角形的性质:
全等三角形的对应边相等;对应角相等。
几何语言:如果△ABC≌△DEF,则∠A=∠D,∠B=∠E,∠C=∠F,AB=DE,AC=DF,BC=EF。
注意:(1)两个三角形全等是对应边和对应角相等的前提。如果没有全等三角形,就没有对应边相等,对应角相等。
(2)利用全等三角形的性质解题时,一定要注意“对应”二字,在用字母表示时,也要对应着写,两个对应角所对的边一定是对应边。
(3)两个三角形全等,就是两个三角形能够完 ( http: / / www.21cnjy.com )全重合。所以不仅对应边相等,对应角相等,对应角平分线、对应高线和对应中线也相等,而且它们的周长和面积也相等。
(4)三角形全等具有传递性。
5、三角形全等的判定条件:(重点)
(1)两边及其夹角分别对应相等的两个三角形全等;简写作:“SAS”。
(2)两角及其夹边分别对应相等的两个三角形全等;简写作:“ASA”。
(3)两角及其中一个角的对边分别相等的两个三角形全等;简写作:“AAS”。
(4)三边分别对应相等的两个三角形全等;简写作:“SSS”。
(5)用“HL”证明两个直角三角形全等。
应用举例:如图,四边形ABCD的对角线AC与BD相交于O点,
∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;(2)BO=DO.
6、三角形的稳定性:如果一个三角形三边长度确定,那么这个三角形的形状和大小就完全确定。三角形的这个性质叫做三角形的稳定性。
应用举例:工人师傅造门时,常用木条EF固定门框ABCD(如图所示),使其形状不变,这种做法的依据是( )
A、两点之间线段最短 B、长方形的对称性
C、长方形四个角都是直角 D、三角形的稳定性
7、尺规作角平分线和垂线:(1)角平分线的作法;(2)过直线外一点作已知直线的垂线。
应用举例:已知:△ABC是等边三角形.
(1)用直尺和圆规分别作△ABC的角平分线BE、CD,BE,CD交于点O
(保留作图痕迹,不写作法);
(2)过点C画射线CF⊥BC,垂足为C,CF交射线BE与点F.求证:
△OCF是等边三角形;
(3)若AB=2,请直接写出△OCF的面积.
三、典型例题:
1、已知,△ABC≌△DE ( http: / / www.21cnjy.com )F,△ABC的周长为12cm,AB=4cm,BC=5cm,则DE= ,EF= ,DF= .
2、如图,△ABC≌△AEC,B和E为对应顶点,∠B=40°,
∠ACB=70°,求△AEC各个内角的度数。
3、△ABC绕点A旋转得到△ADE,∠B=28°,∠E=95°,则
∠BAD的度数为( )
A、75° B、57° C、55° D、77°
4、如图,在Rt△ABC中,∠ACB=90°,且AC=BC=4cm。已知
△BCD≌△ACE。求四边形AECD面积。
5、已知:如图,点D、E在BC上,且BD=CE,AD=AE,
求证:AB=AC.
6、已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
7、已知:BE⊥CD,BE=DE,BC=DA,
求证:①△BEC≌△DEA;
②DF⊥BC.
8、如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,
BC、DE交于点O.
求证:(1) △ABC≌△AED; (2) OB=OE
说明:证明两个三角形全等时图形中常用的隐含条件:
判定两个三角形全等,寻找条件时,应该注 ( http: / / www.21cnjy.com )意图形中的隐含条件,常见的有:(1)公共边或公共角相等;(2)对顶角相等;(3)等边加(或减)等边,其和(或其差)仍相等;(4)等角加(或减)等角,其和(或差)仍相等;(5)同角或等角的余角(或补角)相等;(6)有中线或角平分线的定义得出线段或角相等;(7)由垂直定义得出直角相等。另外,一些自然规律如:“太阳光线可以看成是平行的”,“光的反射角等于入射角”等也是常用的隐含条件。
四、基础训练:
1、如图,已知AB=AD,要使△ABC≌△ADC,可增加条件 ,
理由是 定理。
2、下列说法中正确的是( )
A、两个直角三角形全等 B、两个等腰三角形全等
C、两个等边三角形全等 D、两条直角边对应相等的直角三角形全等
3、如图,△ABC中,∠C=90 ,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,
且CD=6cm,则DE的长为( )
A、4cm B、6cm C、8cm D、10cm
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
4、三角形内到三条边的距离相等的点是( )
A、三角形的三条角平分线的交点 B、三角形的三条高的交点
C、三角形的三条中线的交点 D、三角形的三边的垂直平分线的交点
5、三角形内到三个顶点的距离相等的点是( )
A、三角形的三条角平分线的交点 B、三角形的三条高的交点
C、三角形的三条中线的交点 D、三角形的三边的垂直平分线的交点
6、在△ABC中,∠A=70 ,∠B=40 ,则△ABC是( )
A、钝角三角形 B、等腰三角形 C、等边三角形
D、等腰直角三角形
7、如图,AE=BE,∠C=∠D,求证:△ABC≌△BAD。
8、如图,在△ABC和△DEF中, ( http: / / www.21cnjy.com )B、E、C、F在同一直线上,下面有四个条件,请你从中选三个作为题设,余下的一个作为结论,写出一个正确的命题,并加以证明。
①AB=DE, ②AC=DF, ③∠ABC=∠DEF, ④BE=CF.
解:我写的真命题是:
在△ABC和△DEF中,
如果 ,
那么 。(不能只填序号)
证明如下:
9、已知:AC ,BD相交于点O,AO=OC,再添加一个什么条件,使两个三角形全等?
10、如图,在△ABC和△EFD中,AD=FC,AB=FE,当添加条件_______时,就可得△ABC≌△EFD(SSS)
11、如图,点E、F在AB上,且AF=BE,AC=BD,AC∥BD.求证:CF∥DE
12、如图1,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于D,
(1)求证: △BCE≌△CAD;
(2)猜想:AD,DE,BE的数量关系为 (不需证明);
(3)当CE绕点C旋转到图2位置时,猜想线段AD,DE,BE之间又有怎样的数量关系,并证明你的结论.
D
C
B
A
O
1
2
3
4
A
B
C
D
E
B
C
D
E
F
A
B
C
D
E
F
A
E
B
D
A
图2
C
B
E
C
D
A
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
