14.1.4整式的乘法(2) 课件(共16张PPT)
文档属性
| 名称 | 14.1.4整式的乘法(2) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
人教版 八年级数学上
14.1.4整式的乘法(2)
学习目标
1.掌握单项式与多项式的乘法运算法则.(重点)
2.灵活运用单项式与多项式的乘法运算法则进行计算.(难点)
温故旧知
2.小试身手:
1.说一说单项式与单项式相乘的乘法法则?
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于
只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
解:
合作探究
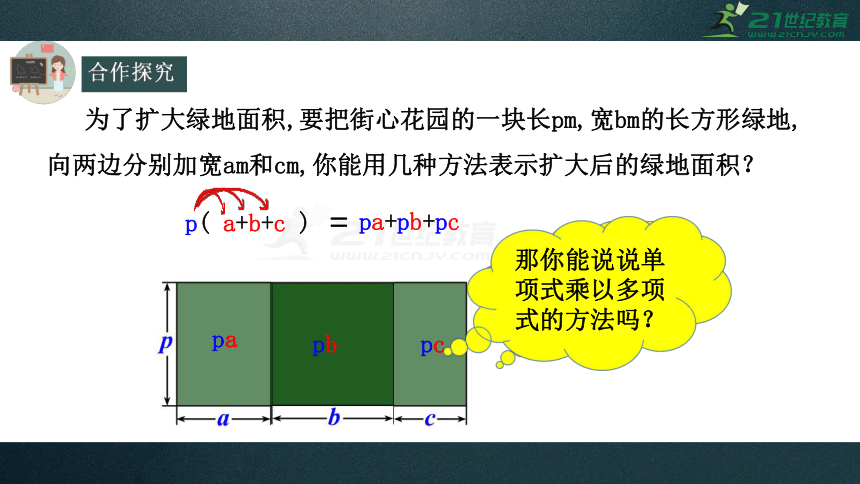
为了扩大绿地面积,要把街心花园的一块长pm,宽bm的长方形绿地,向两边分别加宽am和cm,你能用几种方法表示扩大后的绿地面积?
p( a+b+c )
pa+pb+pc
pa
pc
=
pb
你能根据分配律得到这个等式吗?
那你能说说单项式乘以多项式的方法吗?
合作探究
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
p( a+b+c )
pa+pb+pc
=
典例精析
例1 计算:
(1)(-4x2)·(3x+1);
解:(1)(-4x2)·(3x+1)
=
=-12x3-4x2
+
(2)原式
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
-4x2·3x
(-4x2)·1
小试牛刀
1.计算:
(1)3a·(5a-2b);
(2)(x-3y)·(-6y);
解:(1)3a(5a-2b)
=3a×5a-3a×2b
=15a2-6ab
(2)(x-3y)(-6y)
=x×(-6y)+(-3y)×(-6y)
=-6xy+18y2
小试牛刀
2.化简: x(x-1)+2x(x+1)-3x(2x-5).
解:x(x-1)+2x(x+1)-3x(2x-5)
=x2-x+2x2+2x+-6x2+15x
=-3x2+16x
小试牛刀
3.如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
因为展开式中不含x3项
所以n=0.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1.说一说单项式与多项式相乘的运算法则?
2.在计算中应注意哪些问题?
实战演练
1.计算-4x(3x2-1)的结果是( )
A.-7x3+4x B.-7x3-4x C.-12x3+4x D.12x2-4x
2.下列计算正确的是( )
A.(-4x)(2x2+3x-1)=-8x3-12x2-4x
B.(6xy2-4x2y)·3xy=6xy2-12x3y2
C.(-x)(2x+x2-1)=-x3-2x2+1
D.(-3x2y)(-2xy+3yz+1)=6x3y2-9x2y2z-3x2y
C
D
实战演练
3.已知x2+3x=-2,则代数式5+x(x+3)的值为_____.
3
4.现规定一种运算“*”:a*b=a(a-b),其中a,b为有理数,则
a*b-b*(a-b)等于 .
a2-2b2
3.a2(-a+b-c)与-a(a2-ab+ac)的关系是( )
A.相等 B.互为相反数
C.前式是后式的-a倍 D.前式是后式的a倍
A
实战演练
5.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
实战演练
6.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到
的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
课后作业
教材105页练习题第4题
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
14.1.4整式的乘法(2)
学习目标
1.掌握单项式与多项式的乘法运算法则.(重点)
2.灵活运用单项式与多项式的乘法运算法则进行计算.(难点)
温故旧知
2.小试身手:
1.说一说单项式与单项式相乘的乘法法则?
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于
只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
解:
合作探究
为了扩大绿地面积,要把街心花园的一块长pm,宽bm的长方形绿地,向两边分别加宽am和cm,你能用几种方法表示扩大后的绿地面积?
p( a+b+c )
pa+pb+pc
pa
pc
=
pb
你能根据分配律得到这个等式吗?
那你能说说单项式乘以多项式的方法吗?
合作探究
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
单项式乘以多项式的法则:
p( a+b+c )
pa+pb+pc
=
典例精析
例1 计算:
(1)(-4x2)·(3x+1);
解:(1)(-4x2)·(3x+1)
=
=-12x3-4x2
+
(2)原式
单项式与多项式相乘
单项式与单项式相乘
乘法分配律
转化
-4x2·3x
(-4x2)·1
小试牛刀
1.计算:
(1)3a·(5a-2b);
(2)(x-3y)·(-6y);
解:(1)3a(5a-2b)
=3a×5a-3a×2b
=15a2-6ab
(2)(x-3y)(-6y)
=x×(-6y)+(-3y)×(-6y)
=-6xy+18y2
小试牛刀
2.化简: x(x-1)+2x(x+1)-3x(2x-5).
解:x(x-1)+2x(x+1)-3x(2x-5)
=x2-x+2x2+2x+-6x2+15x
=-3x2+16x
小试牛刀
3.如果(-3x)2(x2-2nx+2)的展开式中不含x3项,求n的值.
解:(-3x)2(x2-2nx+2)
=9x2(x2-2nx+2)
=9x4-18nx3+18x2.
因为展开式中不含x3项
所以n=0.
课堂小结
今天我们收获了哪些知识?(畅所欲言)
1.说一说单项式与多项式相乘的运算法则?
2.在计算中应注意哪些问题?
实战演练
1.计算-4x(3x2-1)的结果是( )
A.-7x3+4x B.-7x3-4x C.-12x3+4x D.12x2-4x
2.下列计算正确的是( )
A.(-4x)(2x2+3x-1)=-8x3-12x2-4x
B.(6xy2-4x2y)·3xy=6xy2-12x3y2
C.(-x)(2x+x2-1)=-x3-2x2+1
D.(-3x2y)(-2xy+3yz+1)=6x3y2-9x2y2z-3x2y
C
D
实战演练
3.已知x2+3x=-2,则代数式5+x(x+3)的值为_____.
3
4.现规定一种运算“*”:a*b=a(a-b),其中a,b为有理数,则
a*b-b*(a-b)等于 .
a2-2b2
3.a2(-a+b-c)与-a(a2-ab+ac)的关系是( )
A.相等 B.互为相反数
C.前式是后式的-a倍 D.前式是后式的a倍
A
实战演练
5.计算:-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+(-5x) ·x2y+(-5x) ·(-xy2)
=-2x3 y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3 y+3x2y2.
实战演练
6.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到
的答案是x2-2x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则
∴A=4x2-2x+1.
∴A·(-3x2)=(4x2-2x+1)(-3x2)
A+(-3x2)=x2-2x+1,
=-12x4+6x3-3x2.
课后作业
教材105页练习题第4题
https://www.21cnjy.com/help/help_extract.php
