选择必修第二册 第四章 4.2.2 等差数列的前n项和公式(第1课时)(共27张PPT)
文档属性
| 名称 | 选择必修第二册 第四章 4.2.2 等差数列的前n项和公式(第1课时)(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 09:07:05 | ||
图片预览







文档简介
(共27张PPT)
选择必修2
第四章 数列
4.2 等差数列
4.2.2 等差数列的前n项和公式(第1课时)
教学目标
学习目标 数学素养
1.掌握等差数列前n项和公式的推导方法. 1.数学抽象素养和逻辑推理素养.
2.掌握等差数列前n项和公式,理解等差数列的通项公式与前n项和公式的关系. 2.逻辑推理素养和数学运算素养.
3.掌握等差数列前n项和公式的简单应用. 3.逻辑推理素养和数学运算素养.
温故知新
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
d>0时,{an}是递增数列;d<0时,{an}是递减数列;d=0时,{an}是常数列.
温故知新
已知是等差数列,公差为,
⑴{an}中每隔相同的项抽出来的项按照原来的顺序排列,构成的新数列仍然是等差数列.即,…()是公差为md的等差数列.
⑵数列(b为常数,b≠0)是公差为bd的等差数列;
⑷{ban+c}(b,c是常数)是公差为bd的等差数列.
⑸若{an},{bn}分别是公差为d1,d2的等差数列,则数列{pan+qbn}(p,q是常数)是公差为pd1+qd2的等差数列.
⑶{c+an}(c为任一常数)是公差为d的等差数列;
4.等差数列的性质
⑹若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
知新探究
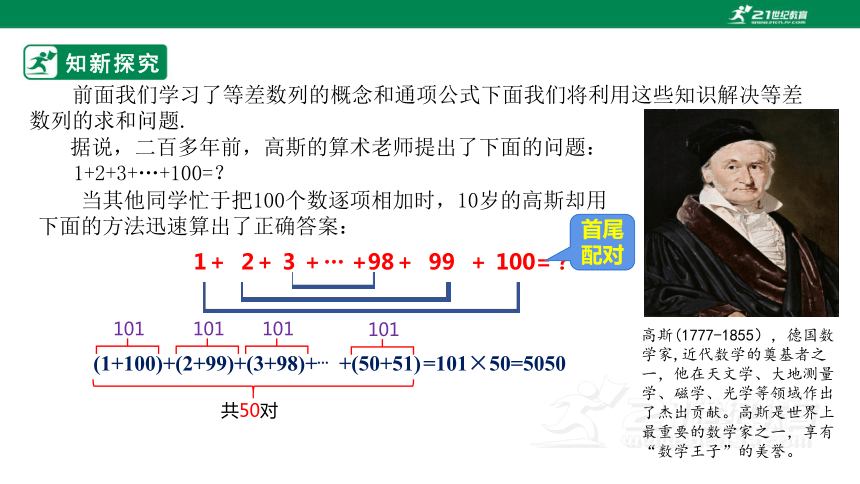
前面我们学习了等差数列的概念和通项公式下面我们将利用这些知识解决等差数列的求和问题.
高斯(1777-1855),德国数学家,近代数学的奠基者之一,他在天文学、大地测量学、磁学、光学等领域作出了杰出贡献。高斯是世界上最重要的数学家之一,享有“数学王子”的美誉。
据说,二百多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
1+ 2+ 3 +… +98+ 99 + 100=?
(1+100)+(2+99)+(3+98)+ +(50+51)
=101×50=5050
101
101
101
101
共50对
首尾配对
知新探究
高斯的算法实际上解决了求等差数列
1,2,3,…,n,… ①
前100项的和的问题.
(a1+a100)+(a2+a99)+…+(a50+a51)=101×50=5050.
可以发现,高斯在计算中利用了
a1+a100=a2+a99=…=a50+a51
对于数列①,设an=n,那么高斯的算法可以表示为
从而简化了运算.
这就是我们上一小节学习的性质:
你能说说高斯在求和过程中利用了数列①什么性质吗?你能从中得到求数列①的前n项和的方法吗?
若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
你能用高斯的方法求1+2+…+100+101吗?
知新探究
将上述方法推广到一般,可以得到:
当n为偶数时,有.
于是有
.
当n为奇数时,有
.
.
.
∴对于任意的正整数n,都有
新知探究
如果对公式作变形,可得
2Sn=2(1+2+3+…+n)=n(n+1),
受此启发,我们得到下面的方法:
它相当于两个Sn相加,而结果变成了n个(n+1)相加.
我们发现,在求前n个正整数的和时,要对n分奇数、偶数讨论,比较麻烦.能否设法避免分类讨论?
Sn= 1 + 2 + 3 + …… + (n 2) + (n 1) + n
Sn= n + (n 1) + (n 2) + …… + 3 + 2 + 1
2Sn=
∴
知新探究
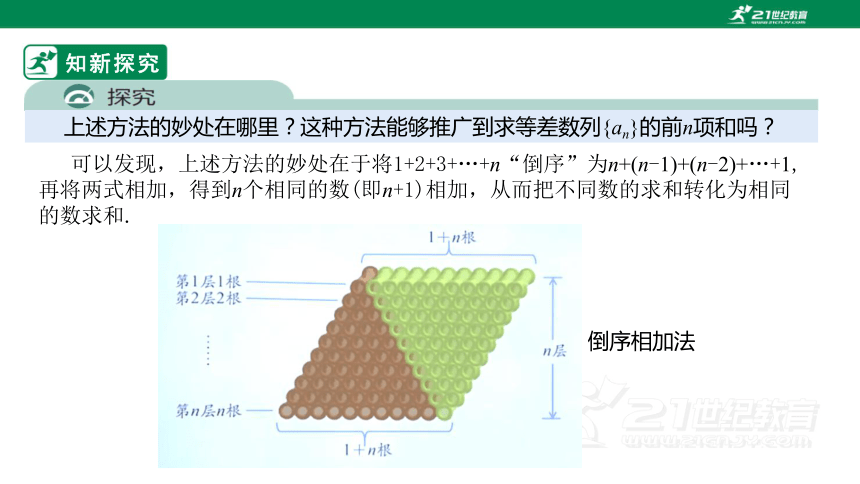
可以发现,上述方法的妙处在于将1+2+3+…+n“倒序”为n+(n-1)+(n-2)+…+1,
再将两式相加,得到n个相同的数(即n+1)相加,从而把不同数的求和转化为相同的数求和.
上述方法的妙处在哪里?这种方法能够推广到求等差数列{an}的前n项和吗?
倒序相加法
知新探究
对于等差数列{an},因为,由上述方法启示,我们用两种方法表示Sn:
②
③
.
②+③,得
.
上述方法的妙处在哪里?这种方法能够推广到求等差数列{an}的前n项和吗?
n个
.
∴.
倒序相加法
知新探究
对于等差数列{an},利用公式⑴,只要已知等差数列{an}的首项a1和末项an,就可以求得前n项和Sn.另外,如果已知首项a1和公差d,这个数列就完全确定了,所以我们也可以用a1和d来表示Sn.
由此得到等差数列{an}的前n项和公式
把等差数列通项公式an=a1+(n-1)d代入公式⑴,可得
.
⑴
将⑴变形可得
,所以就是等差数列{an}前n项的平均数.实际上,我们就是利用等差数列的这一重要特性来推导它的前n项和的.你还能发现这一特性的一些应用吗?
.
⑵
.
an=a1+(n-1)d
.
知新探究
∵等差数列{an}的通项公式an=a1+(n-1)d,
∴
.
.
.
⑵
不从公式⑴出发,你能用其他方法得到公式⑵吗?
解:
.
公式⑵可化为,
∴当d≠0时,Sn是关于n的不含常数项的二次函数,形如Sn=An2+Bn.
知新探究
等差数列{an},公式中涉及四个量:Sn,n,a1,an;
公式中也涉及四个量:Sn,n,a1,d.结合等差数列{an}的通项公式an=a1+(n-1)d,对于等差数列中的五个量:Sn,n,a1,an,d,已知其中的三个量就可以求出另外的两个量.
等差数列{an}的前n项和公式与梯形面积公式类似,可对比记忆为上底是“a1”,下底是“an”,高是“n”.
知新探究
【例1】 已知{an}是等差数列.
⑴若a1=7, =101,求;
⑵若a1=2, =,求;
⑶若=,d=, =-5,求.
解:
⑴∵a1=7, =101,根据公式,可得
.
⑵∵a1=2, ,
∴,
∴.
知新探究
【例1】 已知{an}是等差数列.
⑴若a1=7, =101,求;
⑵若a1=2, =,求;
⑶若,d=, =-5,求.
解:
⑶把,d=, =-5代入,得
.
整理,得 n2-7n-60=0,
解得 n=12,或n=-5(舍去).
∴n=12.
初试身手
⑴∵a1=1,an=-512,Sn=-1022,由,可得
1.已知等差数列{an}的首项为a1, 公差为d.
⑴已知a1=1,an=-512,Sn=-1022,求d;
⑵已知a1=4,S8=172,求a8和d;
⑵∵a1=4,S8=172,由,可得
解:
-1022=,
172=,
解得n=4,
∴1+(4-1)d=-512,
∴d=-137.
解得a8=39,
∴4+(8-1)d=39,
∴d=5.
初试身手
⑶∵a4=9,a9=-6,
1.已知等差数列{an}的首项为a1, 公差为d.
⑶已知a4=9,a9=-6,若Sn=63,求n的值;
∴Sn=,
解:
化简整理,得 n2-13n+42=0,
解得n=6或n=7.
∴,
解得,
知新探究
【例2】已知一个等 差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
解:
由题意,知S10=310,S20=1220,
整理,得,
,
解方程组,得,
所以,由所给可以确定等差数列的首项和公差.
分析:把已知条件代入等差数列前n项和公式⑵后,可得到两个关于a1与d的二元一次方程.解这两个二元一次方程所组成的方程组,就可以求得a1和d.
把它们代入公式,得
初试身手
⑴方法1:∵S12=84,S20=460,
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S28=1092.
解:
∴,
解得,
由,可得
初试身手
⑴方法2:设等差数列{an}的前n项和Sn=an2+bn.
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S28==1092.
解:
∴,
解得,
∵S12=84,S20=460,
∴Sn=2n2-17n,
初试身手
⑵方法1:∵a1+ a2+ a3=-24,a18+ a19+ a20=78,
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S20==180.
解:
∴,
解得,
∴S20==180.
方法2:∵a1+ a2+ a3=-24,a18+ a19+ a20=78,
由a1+a20=a2+a19=a3+a18=…,得
∴a1+ a2+ a3+a18+ a19+ a20=3(a1+a20)=-24+78=54
∴a1+a20=18
知新探究
根据等差数列的前n项和构造新的等差数列的两种方法
已知等差数列{an}的前n项和Sn,可以构造出新的等差数列,从而利用等差数列的相关知识解题.常见的构造方法有:
⑴Sk,S2k-Sk,S3k-S2k,…是等差数列,公差为数列{an}的公差的k2倍;
⑵数列{}是等差数列,公差为数列{an}的公差的.
事实上,=An+B(A,B为常数) {}为等差数列,且有成等差数列,其实质是Sm,S2m-Sm,S3m-S2m成等差数列的变形.
课堂小结
1.等差数列前n项和的公式
. ⑴
. ⑵
公式⑵可化为.
2.等差数列前n项和公式的推导方法
倒序求和法
3. 公式的应用
①当已知首项、末项和项数时,用前一个公式较为简便;当已知首项、公差和项数时,用后一个公式较好.
②两个公式共涉及a1、d、n、an及Sn五个基本量,依据方程的思想,在五个基本量中要知道三个基本量可求其它基本量,这也就是我们所说的“知三求二”.
作业布置
作业: P23 练习 第3,4,5题
P24-25 习题4.2 第1,3题.
补充:
1.一个等差数列的前12项的和为354,前12项中偶数项的和与奇数项的和之比为32∶27,则该数列的公差为________.
2.记Sn为等差数列{an}的前n项和.若a1≠0,a2=3a1,则= .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修2
第四章 数列
4.2 等差数列
4.2.2 等差数列的前n项和公式(第1课时)
教学目标
学习目标 数学素养
1.掌握等差数列前n项和公式的推导方法. 1.数学抽象素养和逻辑推理素养.
2.掌握等差数列前n项和公式,理解等差数列的通项公式与前n项和公式的关系. 2.逻辑推理素养和数学运算素养.
3.掌握等差数列前n项和公式的简单应用. 3.逻辑推理素养和数学运算素养.
温故知新
1.等差数列的概念
一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列. 这个常数叫做等差数列的公差通常用字母d表示.
2.等差中项
等差数列的符号语言:an-an-1 = d (d是常数,n≥2,)
由三个数a,A,b组成的等差数列可以看成是最简单的等差数列.这时,A叫做a与b的等差中项.
2A=a+b或A=.
3.等差数列的通项公式
an=a1+(n-1)d.
首项为a1,公差为d的等差数列{an}的通项公式为
d>0时,{an}是递增数列;d<0时,{an}是递减数列;d=0时,{an}是常数列.
温故知新
已知是等差数列,公差为,
⑴{an}中每隔相同的项抽出来的项按照原来的顺序排列,构成的新数列仍然是等差数列.即,…()是公差为md的等差数列.
⑵数列(b为常数,b≠0)是公差为bd的等差数列;
⑷{ban+c}(b,c是常数)是公差为bd的等差数列.
⑸若{an},{bn}分别是公差为d1,d2的等差数列,则数列{pan+qbn}(p,q是常数)是公差为pd1+qd2的等差数列.
⑶{c+an}(c为任一常数)是公差为d的等差数列;
4.等差数列的性质
⑹若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
知新探究
前面我们学习了等差数列的概念和通项公式下面我们将利用这些知识解决等差数列的求和问题.
高斯(1777-1855),德国数学家,近代数学的奠基者之一,他在天文学、大地测量学、磁学、光学等领域作出了杰出贡献。高斯是世界上最重要的数学家之一,享有“数学王子”的美誉。
据说,二百多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
1+ 2+ 3 +… +98+ 99 + 100=?
(1+100)+(2+99)+(3+98)+ +(50+51)
=101×50=5050
101
101
101
101
共50对
首尾配对
知新探究
高斯的算法实际上解决了求等差数列
1,2,3,…,n,… ①
前100项的和的问题.
(a1+a100)+(a2+a99)+…+(a50+a51)=101×50=5050.
可以发现,高斯在计算中利用了
a1+a100=a2+a99=…=a50+a51
对于数列①,设an=n,那么高斯的算法可以表示为
从而简化了运算.
这就是我们上一小节学习的性质:
你能说说高斯在求和过程中利用了数列①什么性质吗?你能从中得到求数列①的前n项和的方法吗?
若数列{an}是等差数列,p , q , s , t∈N*,且p+q=s+t.则ap+aq=as+at.
你能用高斯的方法求1+2+…+100+101吗?
知新探究
将上述方法推广到一般,可以得到:
当n为偶数时,有.
于是有
.
当n为奇数时,有
.
.
.
∴对于任意的正整数n,都有
新知探究
如果对公式作变形,可得
2Sn=2(1+2+3+…+n)=n(n+1),
受此启发,我们得到下面的方法:
它相当于两个Sn相加,而结果变成了n个(n+1)相加.
我们发现,在求前n个正整数的和时,要对n分奇数、偶数讨论,比较麻烦.能否设法避免分类讨论?
Sn= 1 + 2 + 3 + …… + (n 2) + (n 1) + n
Sn= n + (n 1) + (n 2) + …… + 3 + 2 + 1
2Sn=
∴
知新探究
可以发现,上述方法的妙处在于将1+2+3+…+n“倒序”为n+(n-1)+(n-2)+…+1,
再将两式相加,得到n个相同的数(即n+1)相加,从而把不同数的求和转化为相同的数求和.
上述方法的妙处在哪里?这种方法能够推广到求等差数列{an}的前n项和吗?
倒序相加法
知新探究
对于等差数列{an},因为,由上述方法启示,我们用两种方法表示Sn:
②
③
.
②+③,得
.
上述方法的妙处在哪里?这种方法能够推广到求等差数列{an}的前n项和吗?
n个
.
∴.
倒序相加法
知新探究
对于等差数列{an},利用公式⑴,只要已知等差数列{an}的首项a1和末项an,就可以求得前n项和Sn.另外,如果已知首项a1和公差d,这个数列就完全确定了,所以我们也可以用a1和d来表示Sn.
由此得到等差数列{an}的前n项和公式
把等差数列通项公式an=a1+(n-1)d代入公式⑴,可得
.
⑴
将⑴变形可得
,所以就是等差数列{an}前n项的平均数.实际上,我们就是利用等差数列的这一重要特性来推导它的前n项和的.你还能发现这一特性的一些应用吗?
.
⑵
.
an=a1+(n-1)d
.
知新探究
∵等差数列{an}的通项公式an=a1+(n-1)d,
∴
.
.
.
⑵
不从公式⑴出发,你能用其他方法得到公式⑵吗?
解:
.
公式⑵可化为,
∴当d≠0时,Sn是关于n的不含常数项的二次函数,形如Sn=An2+Bn.
知新探究
等差数列{an},公式中涉及四个量:Sn,n,a1,an;
公式中也涉及四个量:Sn,n,a1,d.结合等差数列{an}的通项公式an=a1+(n-1)d,对于等差数列中的五个量:Sn,n,a1,an,d,已知其中的三个量就可以求出另外的两个量.
等差数列{an}的前n项和公式与梯形面积公式类似,可对比记忆为上底是“a1”,下底是“an”,高是“n”.
知新探究
【例1】 已知{an}是等差数列.
⑴若a1=7, =101,求;
⑵若a1=2, =,求;
⑶若=,d=, =-5,求.
解:
⑴∵a1=7, =101,根据公式,可得
.
⑵∵a1=2, ,
∴,
∴.
知新探究
【例1】 已知{an}是等差数列.
⑴若a1=7, =101,求;
⑵若a1=2, =,求;
⑶若,d=, =-5,求.
解:
⑶把,d=, =-5代入,得
.
整理,得 n2-7n-60=0,
解得 n=12,或n=-5(舍去).
∴n=12.
初试身手
⑴∵a1=1,an=-512,Sn=-1022,由,可得
1.已知等差数列{an}的首项为a1, 公差为d.
⑴已知a1=1,an=-512,Sn=-1022,求d;
⑵已知a1=4,S8=172,求a8和d;
⑵∵a1=4,S8=172,由,可得
解:
-1022=,
172=,
解得n=4,
∴1+(4-1)d=-512,
∴d=-137.
解得a8=39,
∴4+(8-1)d=39,
∴d=5.
初试身手
⑶∵a4=9,a9=-6,
1.已知等差数列{an}的首项为a1, 公差为d.
⑶已知a4=9,a9=-6,若Sn=63,求n的值;
∴Sn=,
解:
化简整理,得 n2-13n+42=0,
解得n=6或n=7.
∴,
解得,
知新探究
【例2】已知一个等 差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗
解:
由题意,知S10=310,S20=1220,
整理,得,
,
解方程组,得,
所以,由所给可以确定等差数列的首项和公差.
分析:把已知条件代入等差数列前n项和公式⑵后,可得到两个关于a1与d的二元一次方程.解这两个二元一次方程所组成的方程组,就可以求得a1和d.
把它们代入公式,得
初试身手
⑴方法1:∵S12=84,S20=460,
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S28=1092.
解:
∴,
解得,
由,可得
初试身手
⑴方法2:设等差数列{an}的前n项和Sn=an2+bn.
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S28==1092.
解:
∴,
解得,
∵S12=84,S20=460,
∴Sn=2n2-17n,
初试身手
⑵方法1:∵a1+ a2+ a3=-24,a18+ a19+ a20=78,
2.已知等差数列{an}的首项为a1, 公差为d.
⑴已知S12=84,S20=460,求S28;
⑵已知a1+ a2+ a3=-24,a18+ a19+ a20=78,求S20 .
∴S20==180.
解:
∴,
解得,
∴S20==180.
方法2:∵a1+ a2+ a3=-24,a18+ a19+ a20=78,
由a1+a20=a2+a19=a3+a18=…,得
∴a1+ a2+ a3+a18+ a19+ a20=3(a1+a20)=-24+78=54
∴a1+a20=18
知新探究
根据等差数列的前n项和构造新的等差数列的两种方法
已知等差数列{an}的前n项和Sn,可以构造出新的等差数列,从而利用等差数列的相关知识解题.常见的构造方法有:
⑴Sk,S2k-Sk,S3k-S2k,…是等差数列,公差为数列{an}的公差的k2倍;
⑵数列{}是等差数列,公差为数列{an}的公差的.
事实上,=An+B(A,B为常数) {}为等差数列,且有成等差数列,其实质是Sm,S2m-Sm,S3m-S2m成等差数列的变形.
课堂小结
1.等差数列前n项和的公式
. ⑴
. ⑵
公式⑵可化为.
2.等差数列前n项和公式的推导方法
倒序求和法
3. 公式的应用
①当已知首项、末项和项数时,用前一个公式较为简便;当已知首项、公差和项数时,用后一个公式较好.
②两个公式共涉及a1、d、n、an及Sn五个基本量,依据方程的思想,在五个基本量中要知道三个基本量可求其它基本量,这也就是我们所说的“知三求二”.
作业布置
作业: P23 练习 第3,4,5题
P24-25 习题4.2 第1,3题.
补充:
1.一个等差数列的前12项的和为354,前12项中偶数项的和与奇数项的和之比为32∶27,则该数列的公差为________.
2.记Sn为等差数列{an}的前n项和.若a1≠0,a2=3a1,则= .
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
