第二十四章 圆 单元测试卷2024-2025学人教版九年级数学上册(含答案)
文档属性
| 名称 | 第二十四章 圆 单元测试卷2024-2025学人教版九年级数学上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 555.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览


文档简介
第二十四章 圆 单元测试卷2024-2025学人教版九年级数学上册
一、单选题(共10题;共30分)
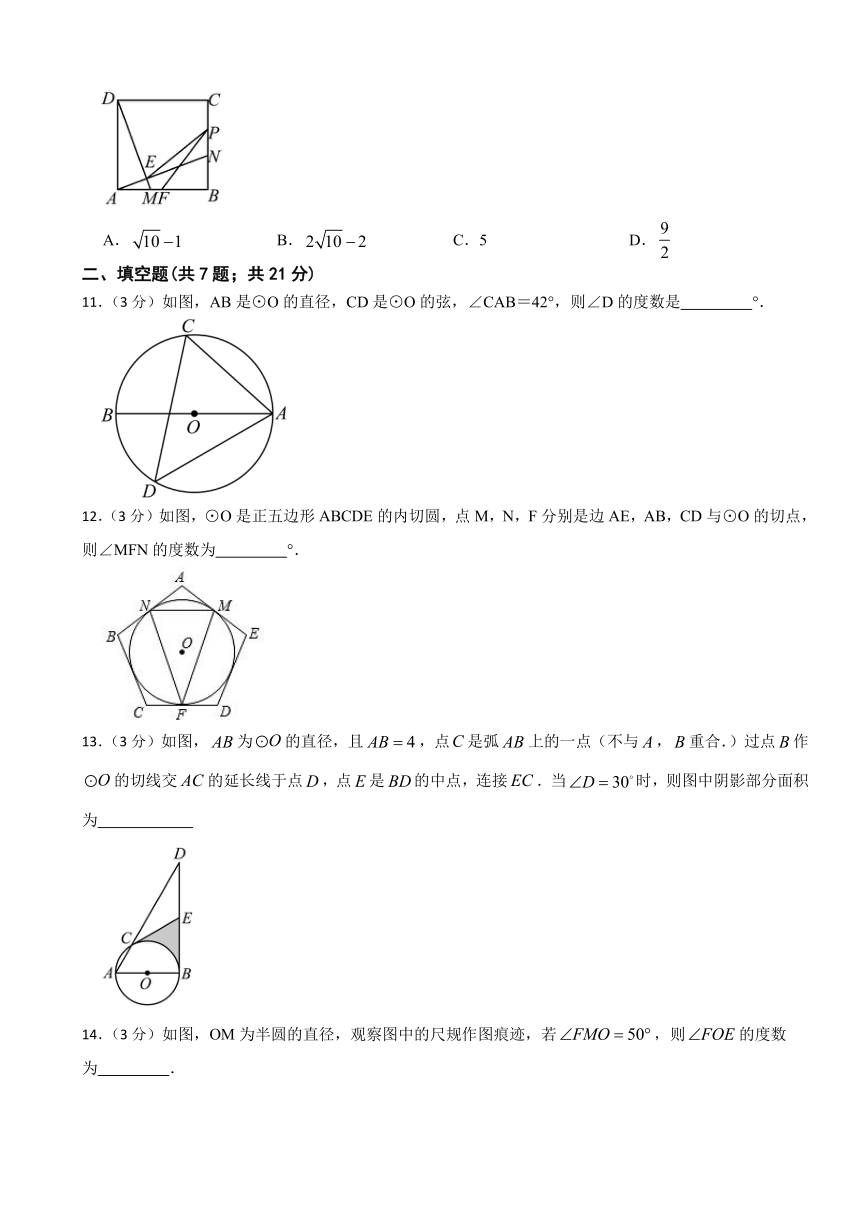
1.(3分)如图,已知A、B、C三点在上,,则的度数为( ).
A. B. C. D.
2.(3分)已知⊙O1与⊙O2的直径长4厘米与8厘米,圆心距为2厘米,那么这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
3.(3分)如图:AB是⊙O的直径,弦CD⊥AB于E,若AB=20,CD=16,则线段BE的长为( )
A.4 B.6 C.8 D.10
4.(3分)如图,点P是边长为6的等边内部一动点,连接BP,CP,AP,满足,D为AP的中点,过点P作,垂足为E,连接DE,则DE长的最小值为( )
A.2 B. C.3 D.
5.(3分) 如图,已知⊙O的半径为1,AB是直径,分别以点A,B为圆心,以AB的长C为半径画弧.两弧相交于C,D两点,则图中阴影部分的面积是( )
A. B. C. D.
6.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
7.(3分) 若正多边形的一个外角是45°,则该正多边形的内角和为( )
A.540° B.720° C.900° D.1080°
8.(3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
9.(3分)如图在给定的中,弦的弦心距,,点E在弦上,且,当面积的为最大时,的长为( )
A. B. C. D.
10.(3分)如图,正方形中,点M,N分别为,上的动点,且,,交于点 E,点 F 为 的中点,点P为上一个动点,连接,.若,则 的最小值为( )
A. B. C.5 D.
二、填空题(共7题;共21分)
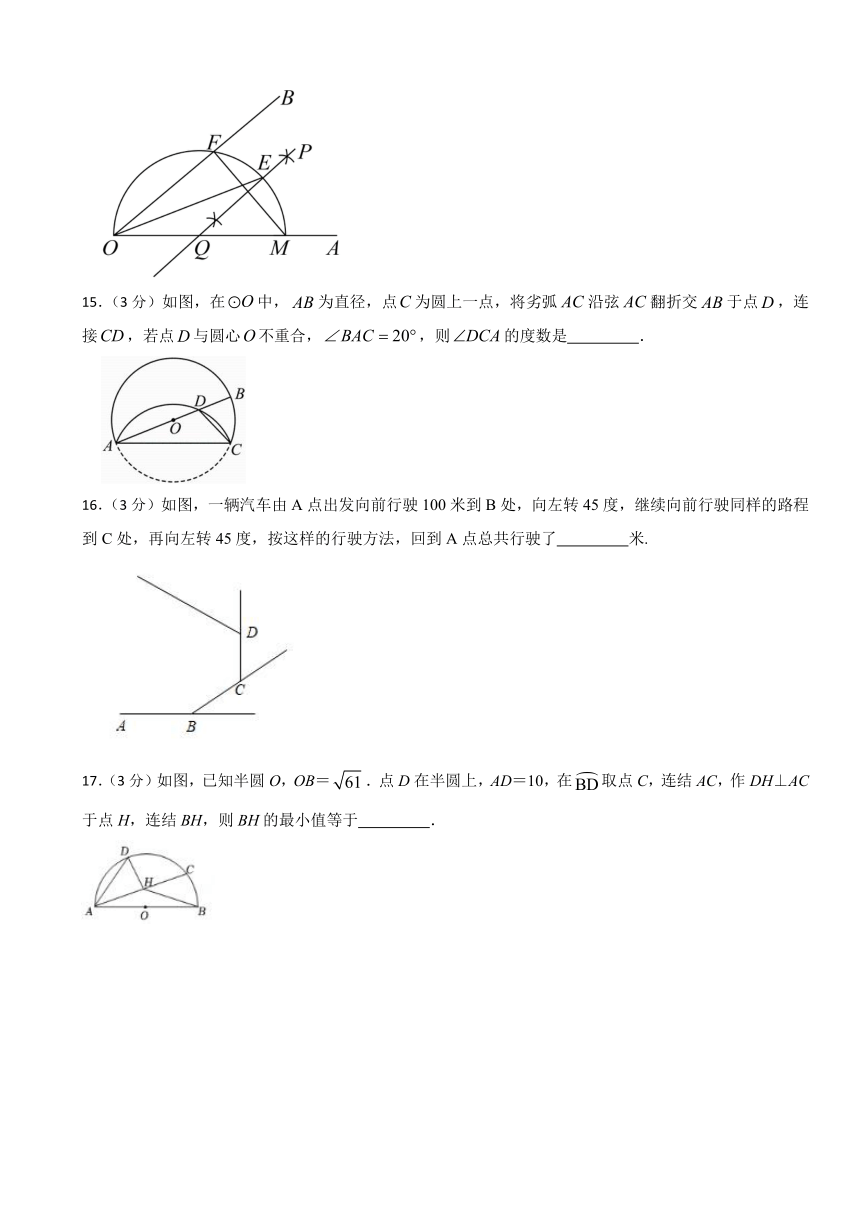
11.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=42°,则∠D的度数是 °.
12.(3分)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 °.
13.(3分)如图,为的直径,且,点是弧上的一点(不与,重合.)过点作的切线交的延长线于点,点是的中点,连接.当时,则图中阴影部分面积为
14.(3分)如图,OM为半圆的直径,观察图中的尺规作图痕迹,若,则的度数为 .
15.(3分)如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点,连接,若点与圆心不重合,,则的度数是 .
16.(3分)如图,一辆汽车由A点出发向前行驶100米到B处,向左转45度,继续向前行驶同样的路程到C处,再向左转45度,按这样的行驶方法,回到A点总共行驶了 米.
17.(3分)如图,已知半圆O,OB=.点D在半圆上,AD=10,在取点C,连结AC,作DH⊥AC于点H,连结BH,则BH的最小值等于 .
三、解答题(共6题;共49分)
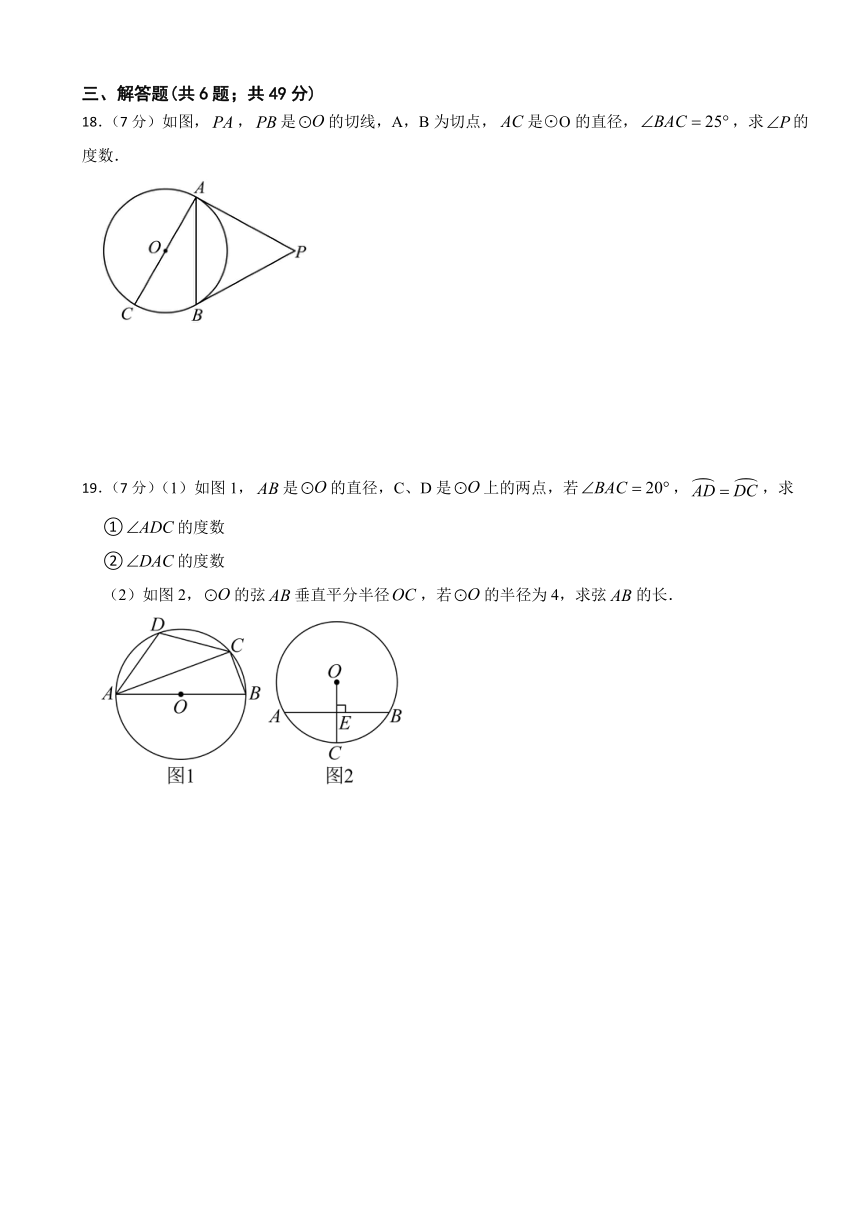
18.(7分)如图,,是的切线,A,B为切点,是⊙O的直径,,求的度数.
19.(7分)(1)如图1,是的直径,C、D是上的两点,若,,求
①的度数
②的度数
(2)如图2,的弦垂直平分半径,若的半径为4,求弦的长.
20.(8分)如图,是的一条弦,,垂足为交于点,点在上.
(1)(4分)若,求的度数;
(2)(4分)若,求的半径长.
21.(8分)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
22.(9分) 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且AD⊥DE于D,与⊙O交于点F.
(1)(4分)判断AC是否是∠DAE的平分线?并说明理由;
(2)(5分)连接OF与AC交于点G,当AG=GC=k时,求切线CE的长.
23.(10分)在矩形中,,,点从点出发沿边以的速度向点移动(点可以与点重合),同时,点从点出发沿以的速度向点移动(点可以与点重合),其中一点到达终点时,另一点随之停止运动.设运动时间为秒.
(1)(3分)如图1,几秒后,的长度等于
(2)(3分)如图1,几秒后,的面积等于四边形面积的
(3)(4分)若以为圆心,为半径作.如图2,若与四边形的边有三个公共点,则的取值范围为_____.(直接写出结果,不需说明理由)
答案解析部分
1.D
2.B
3.A
4.D
5.A
6.B
7.D
8.D
9.B
10.B
11.48
12.36
13.
14.20°
15.50°
16.800
17.8
18.
19.(1),;(2)
20.(1)
(2)
21.
22.(1)解:AC是∠DAE的平分线,理由为:
证明:连接OC、FC,
∵DE是⊙O的切线,∴OC⊥DE,
∵AD⊥DE,
∴∠ADC=∠OCE=90°,
∴AD∥OC,
∴∠2=∠ACO,
∵OA=OC,
∴∠1=∠ACO,
∴∠1=∠2,
∴AC是∠DAE的平分线;
(2)解:
∵AG=CG=k,OA=OC,
∴AC⊥OG,即AG⊥OF,
又∠1=∠2,
∴∠AFG=∠AOG,
∴AF=AO,
又AO=OF,
∴AF=AO=OF,
∴△AOF是等边三角形,
∴∠DAO=∠AOF=60°,
∴∠1=30°,∠COE=60°,
又∠OCE=90°,∠E=30°,
设⊙O的半径为r,在Rt△AOG中,
∵∠1=30°,
∴OG=r,
又AG=k,由勾股定理有:AG2+OG2=AO2,
∴k2+()2=r2,
解得:r=k,
∴AB=k,
同理,在Rt△ADC中,AC=2k,
∵∠2=30°,
∴DC=AC=k,
∴AD=k,
在Rt△ADE中,∠E=30°,
∴AE=2AD=2k,
∴OE=AE﹣r=k,
∴CE=OE=2k;
另解:∠1=∠E=30°,
∴CE=CA=AG+CG=2k.
23.(1)后的长度等于
(2)1秒或2秒后,的面积等于四边形面积的
(3)
一、单选题(共10题;共30分)
1.(3分)如图,已知A、B、C三点在上,,则的度数为( ).
A. B. C. D.
2.(3分)已知⊙O1与⊙O2的直径长4厘米与8厘米,圆心距为2厘米,那么这两圆的位置关系是( )
A.内含 B.内切 C.相交 D.外切
3.(3分)如图:AB是⊙O的直径,弦CD⊥AB于E,若AB=20,CD=16,则线段BE的长为( )
A.4 B.6 C.8 D.10
4.(3分)如图,点P是边长为6的等边内部一动点,连接BP,CP,AP,满足,D为AP的中点,过点P作,垂足为E,连接DE,则DE长的最小值为( )
A.2 B. C.3 D.
5.(3分) 如图,已知⊙O的半径为1,AB是直径,分别以点A,B为圆心,以AB的长C为半径画弧.两弧相交于C,D两点,则图中阴影部分的面积是( )
A. B. C. D.
6.(3分)如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A.5.8 B.3.8 C.1.3 D.2.5
7.(3分) 若正多边形的一个外角是45°,则该正多边形的内角和为( )
A.540° B.720° C.900° D.1080°
8.(3分)如图,在菱形ABCD中,AB=BD,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.给出如下几个结论:①△AED≌△DFB:②GC平分∠BGD;③S四边形BCDG= CG2;④∠BGE的大小为定值.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
9.(3分)如图在给定的中,弦的弦心距,,点E在弦上,且,当面积的为最大时,的长为( )
A. B. C. D.
10.(3分)如图,正方形中,点M,N分别为,上的动点,且,,交于点 E,点 F 为 的中点,点P为上一个动点,连接,.若,则 的最小值为( )
A. B. C.5 D.
二、填空题(共7题;共21分)
11.(3分)如图,AB是⊙O的直径,CD是⊙O的弦,∠CAB=42°,则∠D的度数是 °.
12.(3分)如图,⊙O是正五边形ABCDE的内切圆,点M,N,F分别是边AE,AB,CD与⊙O的切点,则∠MFN的度数为 °.
13.(3分)如图,为的直径,且,点是弧上的一点(不与,重合.)过点作的切线交的延长线于点,点是的中点,连接.当时,则图中阴影部分面积为
14.(3分)如图,OM为半圆的直径,观察图中的尺规作图痕迹,若,则的度数为 .
15.(3分)如图,在中,为直径,点为圆上一点,将劣弧沿弦翻折交于点,连接,若点与圆心不重合,,则的度数是 .
16.(3分)如图,一辆汽车由A点出发向前行驶100米到B处,向左转45度,继续向前行驶同样的路程到C处,再向左转45度,按这样的行驶方法,回到A点总共行驶了 米.
17.(3分)如图,已知半圆O,OB=.点D在半圆上,AD=10,在取点C,连结AC,作DH⊥AC于点H,连结BH,则BH的最小值等于 .
三、解答题(共6题;共49分)
18.(7分)如图,,是的切线,A,B为切点,是⊙O的直径,,求的度数.
19.(7分)(1)如图1,是的直径,C、D是上的两点,若,,求
①的度数
②的度数
(2)如图2,的弦垂直平分半径,若的半径为4,求弦的长.
20.(8分)如图,是的一条弦,,垂足为交于点,点在上.
(1)(4分)若,求的度数;
(2)(4分)若,求的半径长.
21.(8分)如图,已知在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在⊙O及半径OM、OP上,并且∠POM=45°,求正方形的边长.
22.(9分) 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,且AD⊥DE于D,与⊙O交于点F.
(1)(4分)判断AC是否是∠DAE的平分线?并说明理由;
(2)(5分)连接OF与AC交于点G,当AG=GC=k时,求切线CE的长.
23.(10分)在矩形中,,,点从点出发沿边以的速度向点移动(点可以与点重合),同时,点从点出发沿以的速度向点移动(点可以与点重合),其中一点到达终点时,另一点随之停止运动.设运动时间为秒.
(1)(3分)如图1,几秒后,的长度等于
(2)(3分)如图1,几秒后,的面积等于四边形面积的
(3)(4分)若以为圆心,为半径作.如图2,若与四边形的边有三个公共点,则的取值范围为_____.(直接写出结果,不需说明理由)
答案解析部分
1.D
2.B
3.A
4.D
5.A
6.B
7.D
8.D
9.B
10.B
11.48
12.36
13.
14.20°
15.50°
16.800
17.8
18.
19.(1),;(2)
20.(1)
(2)
21.
22.(1)解:AC是∠DAE的平分线,理由为:
证明:连接OC、FC,
∵DE是⊙O的切线,∴OC⊥DE,
∵AD⊥DE,
∴∠ADC=∠OCE=90°,
∴AD∥OC,
∴∠2=∠ACO,
∵OA=OC,
∴∠1=∠ACO,
∴∠1=∠2,
∴AC是∠DAE的平分线;
(2)解:
∵AG=CG=k,OA=OC,
∴AC⊥OG,即AG⊥OF,
又∠1=∠2,
∴∠AFG=∠AOG,
∴AF=AO,
又AO=OF,
∴AF=AO=OF,
∴△AOF是等边三角形,
∴∠DAO=∠AOF=60°,
∴∠1=30°,∠COE=60°,
又∠OCE=90°,∠E=30°,
设⊙O的半径为r,在Rt△AOG中,
∵∠1=30°,
∴OG=r,
又AG=k,由勾股定理有:AG2+OG2=AO2,
∴k2+()2=r2,
解得:r=k,
∴AB=k,
同理,在Rt△ADC中,AC=2k,
∵∠2=30°,
∴DC=AC=k,
∴AD=k,
在Rt△ADE中,∠E=30°,
∴AE=2AD=2k,
∴OE=AE﹣r=k,
∴CE=OE=2k;
另解:∠1=∠E=30°,
∴CE=CA=AG+CG=2k.
23.(1)后的长度等于
(2)1秒或2秒后,的面积等于四边形面积的
(3)
同课章节目录
