5.2《用字母表示数2》课件--人教版数学五上
文档属性
| 名称 | 5.2《用字母表示数2》课件--人教版数学五上 |  | |
| 格式 | zip | ||
| 文件大小 | 35.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 15:18:33 | ||
图片预览






文档简介
(共18张PPT)
简
简
方
方
易
易
程
程
用字母表示数
2
一、复习引入
用字母表示数
一本书a元,买5本同样的书。
5a
既表示总价
又表示总价与单价、数量之间的关系。
二、探索新知
研究一:试一试用字母表示学过运算定律
运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
用字母表示
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a× (b×c)
(a+b)×c=a×c+b×c
二、探索新知
研究二:试一试用字母表示学过的计算公式用S表示面积,
C表示周长
b
a
a
a
S=
c=
c=
S=
a×a
a×b
(a+b)× 2
4a
二、探索新知
运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
用字母表示
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a× (b×c)
(a+b)×c=a×c+b×c
研究一:试一试用字母表示学过运算定律
ab=ba或a·b=b·a
(ab)c=a (bc)或(a·b)·c=a·(b·c)
(a+b) c=ac+bc或(a+b)·c=a·c+b·c
①字母中间的乘号可以记作“· ”,也可以省略不写。
②含有字母的式子中的加、减、除号不能省略。
二、探索新知
研究二:试一试用字母表示学过的计算公式用S表示面积,
C表示周长
a
a
S=
a×a
c=
4a
读作:a的平方
表示:2个a相乘
S=
a×b
c=
(a+b)× 2
b
a
把下面各式写成一个数的平方形式,并读一读。
x×x= 2×2=
比较: a 与2a一样吗?
a·a
a
aa
x
2
ab
2(a+b)
二、探索新知
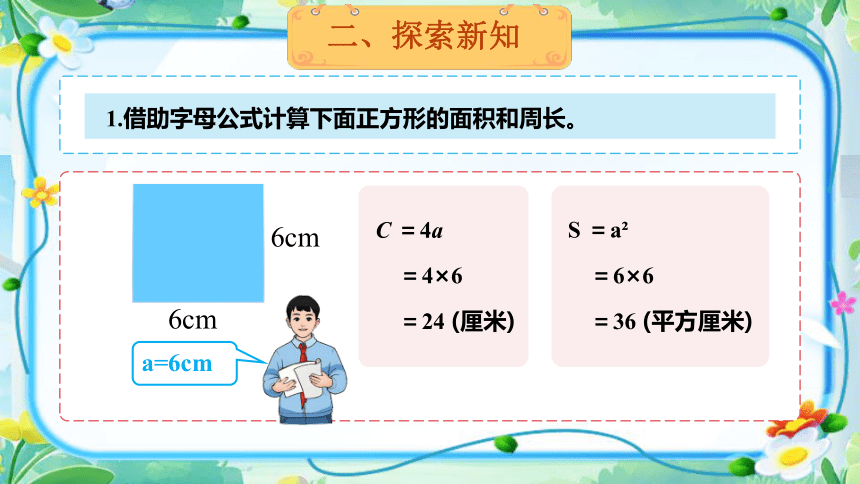
1.借助字母公式计算下面正方形的面积和周长。
6cm
6cm
a=6cm
C =4a
=4×6
=24 (厘米)
S =a
=36 (平方厘米)
=6×6
二、探索新知
2.一个长方形的长是8cm,宽是5cm,它的面积和周长各是多少?
S=a b
=8×5
=40(cm2)
C=2 (a+b)
=2 ×(8+5)
=2× 13
= 26(cm)
三、知识应用
1.省略乘号写出下面各式。
x×x
=x2
b×8
=8b
b×1
=b
a×x
=ax
三、知识应用
2.把结果相等的两个式子连起来。
a2
2.5×2.5
x·x
62
x2
a×2
2.52
6×2
a×a
6×6
三、知识应用
3.在 中填上适当的数或字母。
8× ×125 = 8× ×m
+b= +3 x× =2.6×
3
b
x
2.6
25×a+b× =( + )×25
m
125
25
b
a
三、知识应用
4.(1)小亮每分钟骑行vm,2分钟骑行______m, t分钟
骑行 ______ m。
(2)用v表示速度,t表示时间,s表示路程。s =_______。
(3)如果每分钟骑行260m,骑行30分,骑行的路程是
多少米?
260×30=7800(m)
答:路程是7800 m。
2v
vt
vt
三、知识应用
5.用a表示商品的单价,x表示数量,c表示总价,分别写出它们之间的数量关系。
c=_____________
a=_____________
x=_____________
ax
c÷x
c÷a
从左边选一个公式解决下面的问题。
如果每袋方便面1.5元,6元可以买几袋?
x=c÷a=6÷1.5 =4(袋)答:6元可以买4袋。
三、知识应用
6. 填表并解答问题
1小时=60分钟 c=at=50×60=3000(个)
答:她1小时打3000个字。
工作效率 (个/分) 工作时间 (分) 工作总量
(个)
x 5
m 150
a t c=_____
5x
150÷m
at
王红每分钟打字50个,利用表中的公式计算她1小时打字的个数。
三、知识应用
7.根据右图回答问题。
整个图形的面积是 ac+bc=(a+b)×c
(1)哪一部分的面积是ac?(2)哪一部分的面积是bc?(3)整个图形的面积是多少?
c
b
a
四、本课总结
今天这节课你有什么收获?
用字母表示运算定律,简明易记、便于应用。
1
在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
2
a 读作:a的平方,表示2个a相乘。
3
史料介绍
16世纪,法国和西班牙发动了一场战争,韦达为政府破解敌军密码,使得法国对西班牙的军事动态了如指掌,赢得了最终的胜利。在这件事的启发下,韦达系统地使用字母表示数。他的这一发现,给其他数学家以启发,并为代数思想的产生和发展奠定了坚实的基础。
[法]弗朗索瓦·韦达
(1540-1603)
版权声明
课件版权归属“一起课件”,仅可自用,不可传播,不得用作商业性使用,不得上传至百度文库、等盈利网站。任何侵权行为将被视为版权侵害,侵权者将承担一定的法律责任。
简
简
方
方
易
易
程
程
用字母表示数
2
一、复习引入
用字母表示数
一本书a元,买5本同样的书。
5a
既表示总价
又表示总价与单价、数量之间的关系。
二、探索新知
研究一:试一试用字母表示学过运算定律
运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
用字母表示
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a× (b×c)
(a+b)×c=a×c+b×c
二、探索新知
研究二:试一试用字母表示学过的计算公式用S表示面积,
C表示周长
b
a
a
a
S=
c=
c=
S=
a×a
a×b
(a+b)× 2
4a
二、探索新知
运算定律
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
用字母表示
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a× (b×c)
(a+b)×c=a×c+b×c
研究一:试一试用字母表示学过运算定律
ab=ba或a·b=b·a
(ab)c=a (bc)或(a·b)·c=a·(b·c)
(a+b) c=ac+bc或(a+b)·c=a·c+b·c
①字母中间的乘号可以记作“· ”,也可以省略不写。
②含有字母的式子中的加、减、除号不能省略。
二、探索新知
研究二:试一试用字母表示学过的计算公式用S表示面积,
C表示周长
a
a
S=
a×a
c=
4a
读作:a的平方
表示:2个a相乘
S=
a×b
c=
(a+b)× 2
b
a
把下面各式写成一个数的平方形式,并读一读。
x×x= 2×2=
比较: a 与2a一样吗?
a·a
a
aa
x
2
ab
2(a+b)
二、探索新知
1.借助字母公式计算下面正方形的面积和周长。
6cm
6cm
a=6cm
C =4a
=4×6
=24 (厘米)
S =a
=36 (平方厘米)
=6×6
二、探索新知
2.一个长方形的长是8cm,宽是5cm,它的面积和周长各是多少?
S=a b
=8×5
=40(cm2)
C=2 (a+b)
=2 ×(8+5)
=2× 13
= 26(cm)
三、知识应用
1.省略乘号写出下面各式。
x×x
=x2
b×8
=8b
b×1
=b
a×x
=ax
三、知识应用
2.把结果相等的两个式子连起来。
a2
2.5×2.5
x·x
62
x2
a×2
2.52
6×2
a×a
6×6
三、知识应用
3.在 中填上适当的数或字母。
8× ×125 = 8× ×m
+b= +3 x× =2.6×
3
b
x
2.6
25×a+b× =( + )×25
m
125
25
b
a
三、知识应用
4.(1)小亮每分钟骑行vm,2分钟骑行______m, t分钟
骑行 ______ m。
(2)用v表示速度,t表示时间,s表示路程。s =_______。
(3)如果每分钟骑行260m,骑行30分,骑行的路程是
多少米?
260×30=7800(m)
答:路程是7800 m。
2v
vt
vt
三、知识应用
5.用a表示商品的单价,x表示数量,c表示总价,分别写出它们之间的数量关系。
c=_____________
a=_____________
x=_____________
ax
c÷x
c÷a
从左边选一个公式解决下面的问题。
如果每袋方便面1.5元,6元可以买几袋?
x=c÷a=6÷1.5 =4(袋)答:6元可以买4袋。
三、知识应用
6. 填表并解答问题
1小时=60分钟 c=at=50×60=3000(个)
答:她1小时打3000个字。
工作效率 (个/分) 工作时间 (分) 工作总量
(个)
x 5
m 150
a t c=_____
5x
150÷m
at
王红每分钟打字50个,利用表中的公式计算她1小时打字的个数。
三、知识应用
7.根据右图回答问题。
整个图形的面积是 ac+bc=(a+b)×c
(1)哪一部分的面积是ac?(2)哪一部分的面积是bc?(3)整个图形的面积是多少?
c
b
a
四、本课总结
今天这节课你有什么收获?
用字母表示运算定律,简明易记、便于应用。
1
在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。
2
a 读作:a的平方,表示2个a相乘。
3
史料介绍
16世纪,法国和西班牙发动了一场战争,韦达为政府破解敌军密码,使得法国对西班牙的军事动态了如指掌,赢得了最终的胜利。在这件事的启发下,韦达系统地使用字母表示数。他的这一发现,给其他数学家以启发,并为代数思想的产生和发展奠定了坚实的基础。
[法]弗朗索瓦·韦达
(1540-1603)
版权声明
课件版权归属“一起课件”,仅可自用,不可传播,不得用作商业性使用,不得上传至百度文库、等盈利网站。任何侵权行为将被视为版权侵害,侵权者将承担一定的法律责任。
