2.2.1向量加法运算及其几何意义
文档属性
| 名称 | 2.2.1向量加法运算及其几何意义 |  | |
| 格式 | zip | ||
| 文件大小 | 832.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-16 13:33:59 | ||
图片预览




文档简介
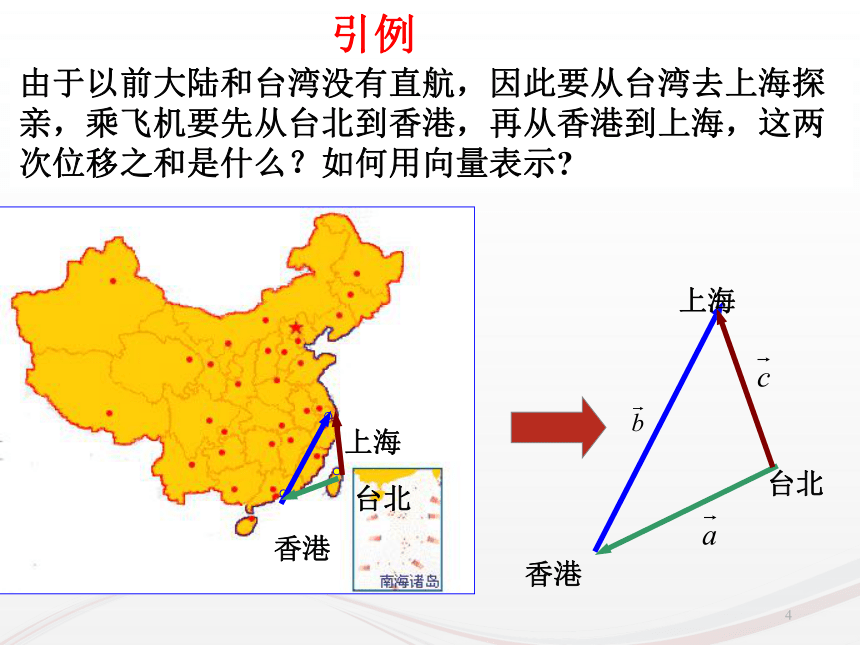
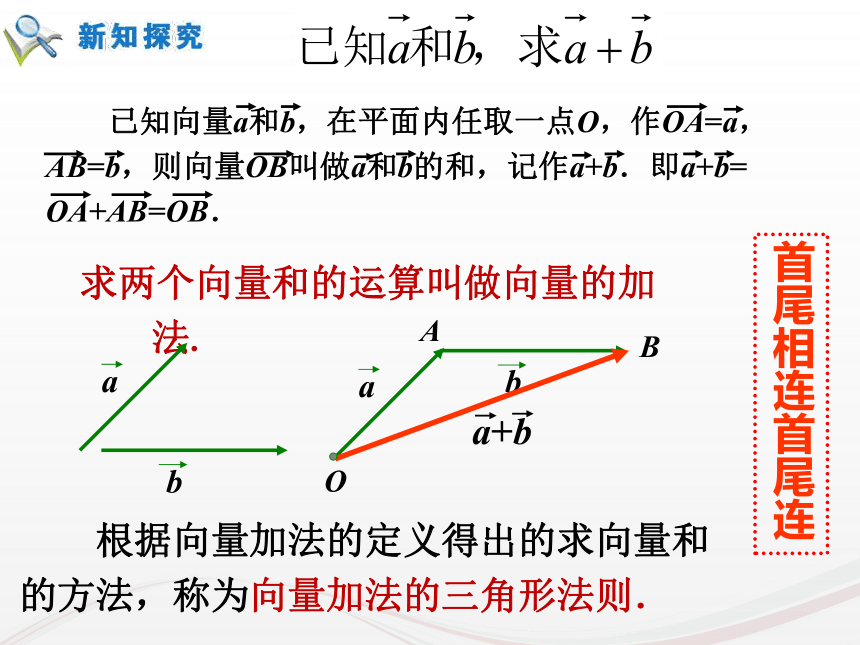
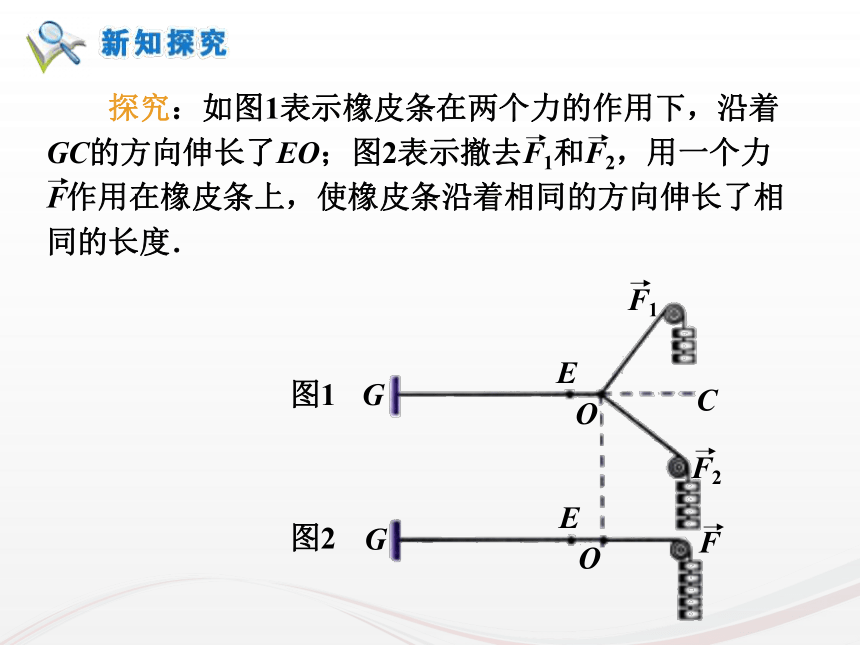
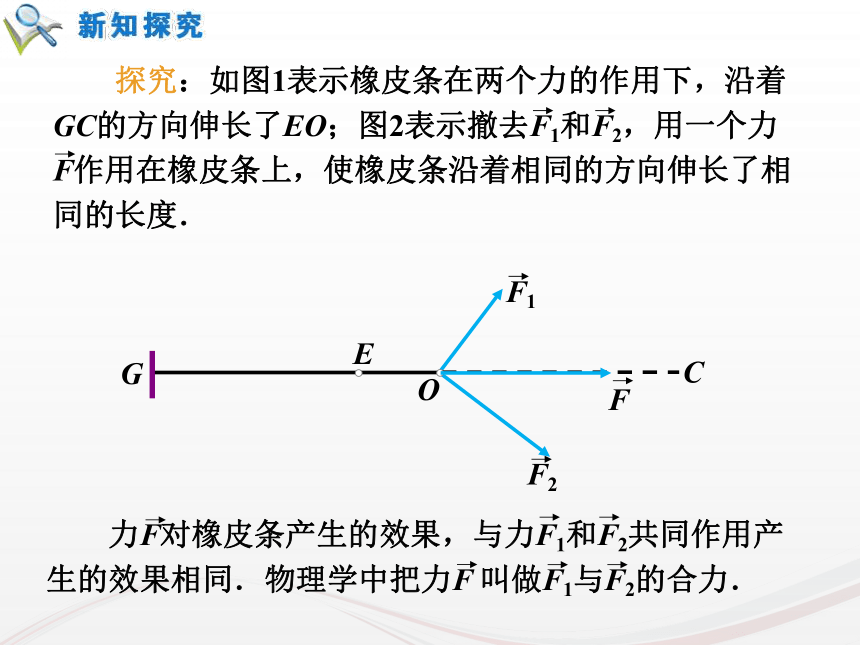
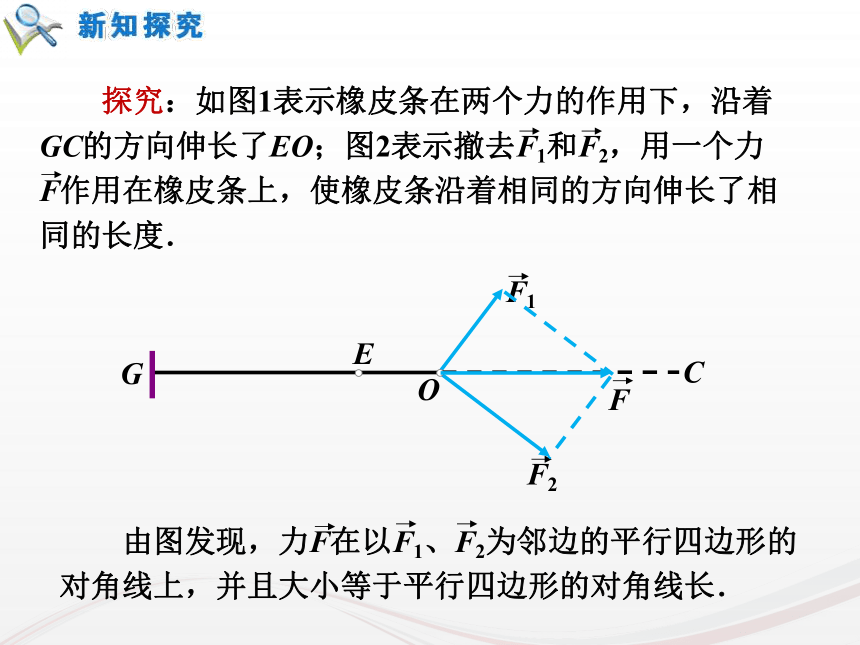
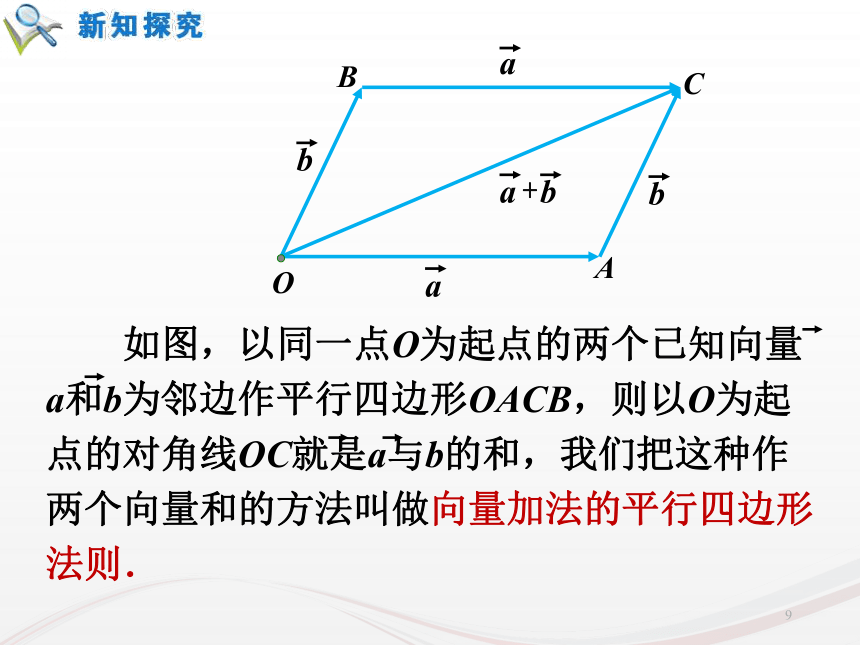
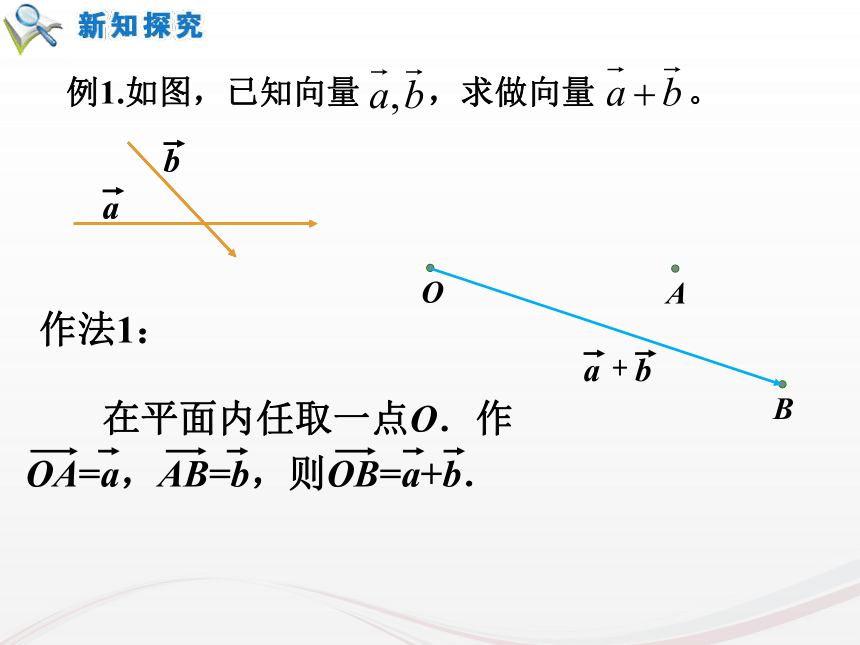
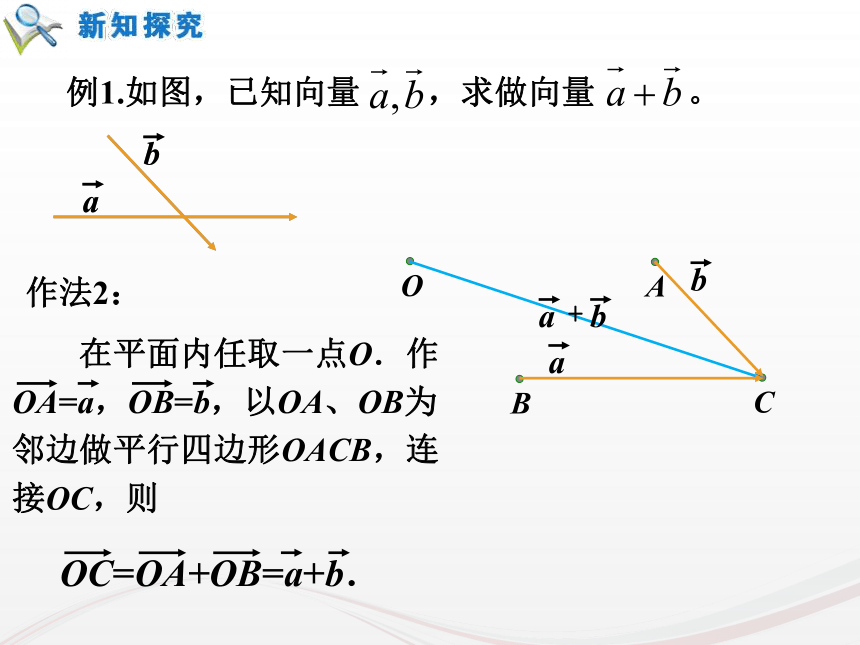
课件33张PPT。复习回顾:1.向量、平行向量、相等向量的含义分别是什么呢?向量:既有方向又有大小的量平行向量:方向相同或相反的向量相等向量:方向相同并且长度相等的向量1复习回顾:2.向量的大小和方向是如何用有向线段表示的呢?什么叫零向量和单位向量?向量的大小:有向线段的长度。向量的方向:有向线段的方向。零向量:长度为零的向量叫零向量。单位向量:长度等于1个单位长度的向量叫 单位向量。22.2.1 向量加法运算及其几何意义由于以前大陆和台湾没有直航,因此要从台湾去上海探亲,乘飞机要先从台北到香港,再从香港到上海,这两次位移之和是什么?如何用向量表示?上海台北香港引例4求两个向量和的运算叫做向量的加法. 根据向量加法的定义得出的求向量和的方法,称为向量加法的三角形法则.首尾相连首尾连ACB9 位移的合成可以看作向量加法三角形法则的物理模型. 力的合成可以看作向量加法平行四边形法则的物理模型.10作法1:例1.如图,已知向量 ,求做向量 。作法2:例1.如图,已知向量 ,求做向量 。课本84页 1如图,已知 用向量加法的平行四边形法则作出 (1)(2)课本84页 2 思考:如下图,当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?方向相同方向相反OABOAB何时取得等号?≤≤16 思考:如下图,当在数轴上表示两个共线向量时,它们的加法与数的加法有什么关系?方向相同方向相反OABOAB7.(2)是否存在a,b,使|a+b|=|a|=|b|?【解析】(2)存在,如图,OA=OB=OC,∠AOB=120°,∠AOC=∠COB=60°.这时的a,b,使|a+b|=|a|=|b|.全优43页能力提高拓展:5.若菱形ABCD的边长为2,则=______.2全优43页基础夯实3.满足条件的平行四边形ABCD是________.全优89页限时规范训练矩形22 数的加法满足交换律与结合律,即对任意a,b∈R,有a+b=b+a,(a+b)+c=a+(b+c)
任意向量a,b的加法是否也满足交换律与结合律?向量加法的运算律交换律结合律以上两个性质可以推广到任意多个向量【例2】 化简下列各式:【解析】=0;全优42页典例剖析根据图示填空:
(1)a+d=____________
(2)c+b=____________课本84页 3练一练课本84页 41.如图所示,O为正六边形的中心,化简下列各式:【解析】全优42页变式训练2.如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:【解析】=0.全优42页变式训练6.若D为△ABC的边BC的中点,△ABC所在平面内有一点P,满足则λ的值为________.2【解析】∴四边形PCAB是平行四边形.由D为△ABC的边BC的中点,全优43页能力提高例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。ADBC例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。ADBC5.在?ABCD的对角线BD的延长线上取两点E,F,使BE=DF,用向量的方法证明四边形AECF也是平行四边形.【证明】又在?ABCD中,又BE=FD且方向相同,故四边形AECF为平行四边形.全优89页限时规范训练
任意向量a,b的加法是否也满足交换律与结合律?向量加法的运算律交换律结合律以上两个性质可以推广到任意多个向量【例2】 化简下列各式:【解析】=0;全优42页典例剖析根据图示填空:
(1)a+d=____________
(2)c+b=____________课本84页 3练一练课本84页 41.如图所示,O为正六边形的中心,化简下列各式:【解析】全优42页变式训练2.如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:【解析】=0.全优42页变式训练6.若D为△ABC的边BC的中点,△ABC所在平面内有一点P,满足则λ的值为________.2【解析】∴四边形PCAB是平行四边形.由D为△ABC的边BC的中点,全优43页能力提高例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。ADBC例2.长江两岸之间没有大桥的地方,常常通过轮船进行运输,
如图所示,一艘船从长江南岸A点出发,以 km/h的速度向
垂直于对岸的方向行驶,同时江水的速度为向东2km/h.
(1)试用向量表示江水速度、船速以及船实际航行的速度;
(2)求船实际航行的速度的大小与方向(用与江水速度的夹
角来表示)。答:船实际航行速度为4km/h,方向与水的流速间的夹角为60o。ADBC5.在?ABCD的对角线BD的延长线上取两点E,F,使BE=DF,用向量的方法证明四边形AECF也是平行四边形.【证明】又在?ABCD中,又BE=FD且方向相同,故四边形AECF为平行四边形.全优89页限时规范训练
