深圳市中考备考百师助学培优课程——第13讲:一、二次函数与反比例函数应用题 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第13讲:一、二次函数与反比例函数应用题 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览








文档简介
罗湖区2024“百师助学”中考数学课程
第十三讲
一、二次函数与反比例函数应用题
罗湖外语初中学校 任平
模块一:一次函数应用题
1、结合具体情境体会一次函数的意义,能根据已知条件(文字、图象、表格)
分析函数关系;会运用待定系数法确定一次函数的表达式
2、能画一次函数的图象,根据图象和表达式y=kx +b(k 0)探索并理解k>0
和k<0时图象的变化情况
3、体会一次函数与二元一次方程的关系
4、能用一次函数解决简单实际问题
实际问题
函数模型
分析模型、结合模型对数学问题求解
例题精讲
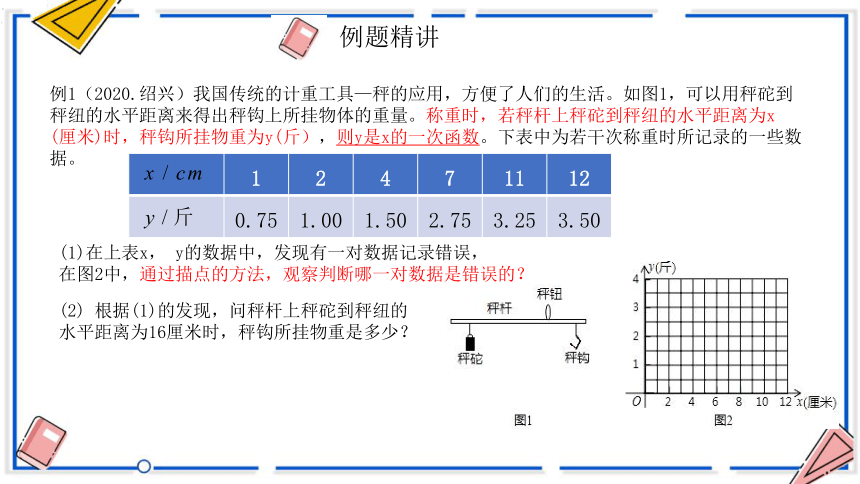
例1(2020.绍兴)我国传统的计重工具—秤的应用,方便了人们的生活。如图1,可以用秤砣到秤纽的水平距离来得出秤钩上所挂物体的重量。称重时,若秤杆上秤砣到秤纽的水平距离为x (厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数。下表中为若干次称重时所记录的一些数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
(1)在上表x, y的数据中,发现有一对数据记录错误,
在图2中,通过描点的方法,观察判断哪一对数据是错误的?
(2) 根据(1)的发现,问秤杆上秤砣到秤纽的
水平距离为16厘米时,秤钩所挂物重是多少?
例题精讲
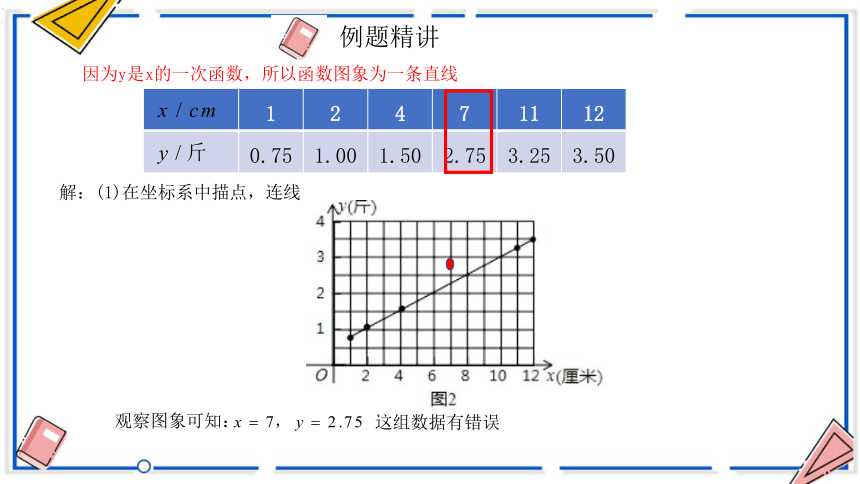
因为y是x的一次函数,所以函数图象为一条直线
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
解:(1)在坐标系中描点,连线
观察图象可知:
这组数据有错误
例题精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
解:
(2) 根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
例题精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日期
销售记录
6月1日
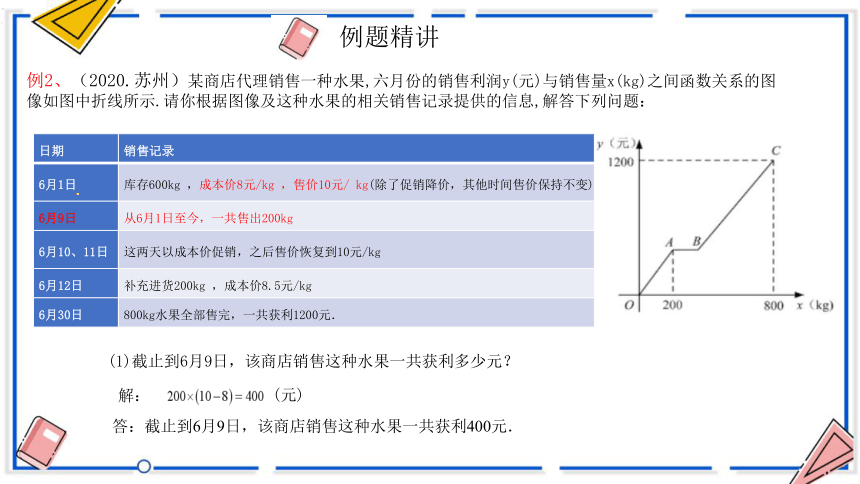
库存600kg ,成本价8元/kg ,售价10元/ kg(除了促销降价,其他时间售价保持不变)
6月9日
从6月1日至今,一共售出200kg
6月10、11日
这两天以成本价促销,之后售价恢复到10元/kg
6月12日
补充进货200kg ,成本价8.5元/kg
6月30日
800kg水果全部售完,一共获利1200元.
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
解:
(元)
答:截止到6月9日,该商店销售这种水果一共获利400元.
例2、(2020.苏州)某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
例题精讲
例2、(2020.苏州)某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日期
销售记录
6月1日
库存600kg ,成本价8元/kg ,售价10元/ kg(除了促销降价,其他时间售价保持不变)
6月9日
从6月1日至今,一共售出200kg
6月10、11日
这两天中先以成本价促销,之后售价恢复到10元/kg到该批水果卖完
6月12日
补充进货200kg ,成本价8.5元/kg
6月30日
800kg水果全部售完,一共获利1200元.
(2)求图像中线段BC所在直线对应的函数表达式.
(800,1200)
促销期间利润不增加
(a,400)
解:设点B的坐标为(a,400),依题意得
解得:
∴点B的坐标为(350,400)
待定系数法
促销卖掉(a-200)kg
[600-(a-200)]×(10-8)
+200×(10-8.5)=1200
设线段BC所在直线的函数表达式为y=kx+b(k≠0)
将B(350,400)、C(800,1200)两点坐标分别代入表达式得
.
∴线段BC所在直线的函数表达式为
例题精讲
例3、(2023.台州)【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲
乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始
放水后每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【建立模型】小组讨论发现:“t=0,h=30”是初始状态下的准确数据,
水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务1:分别计算表中每隔10min水面高度观察值的变化量
任务2:利用t=0时,h=30;t=10时,h=29这两组数据求水面高度h与流水时间t的函数解析式;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
解:任务1:变化量分别为:
29﹣30=﹣1(cm);28.1﹣29=﹣0.9(cm);
27﹣28.1=﹣1.1(cm);25.8﹣27=﹣1.2(cm)
∴每隔10min水面高度观察值的变化量为:
﹣1,﹣0.9,﹣1.1,﹣1.2.
任务2:设水面高度h与流水时间t的函数解析式为
h=kt+b
∵t=0 时,h=30;t=10时,h=29;代入表达式得
∴水面高度h与流水时间t的函数解析式为h=﹣0.1t+30;
解得
例题精讲
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后
每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【反思优化】经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,
存在偏差,小组决定优化函数解析式,减少偏差.通过查阅资料后知道:
t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与
对应h的观察值之差的平方和,记为w;w越小,偏差越小.
任务3:(1)计算任务2得到的函数解析式的w值;
(2)请确定经过(0,30)的一次函数解析式,使得w的值最小;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务2得到h=﹣0.1t+30
任务3:
(1)w=(30﹣30)?+(29﹣29)2+(28﹣28.1)2+(27﹣27)2+(26﹣25.8)2=0.05.
(2)设优化后的函数表达式为 h=mt+30,
w=(0+30﹣30)2+(10m+30﹣29)2+(20m+30﹣28.1)2+(30m+30﹣27)2+(40m+30﹣25.8)2
=3000(m+0.102)2+0.038
∵ 3000>0,函数开口向上,∴当m=﹣0.102时,w的最小值为0.038. 此时h=-0.102t+30
例题精讲
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后
每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【设计刻度】得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,
通过刻度直接读取时间.
任务4:请你简要写出时间刻度的设计方案.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
解:任务4:由任务3可知优化之后的函数关系式为:h= ﹣0.102 t+30 .即每分钟水位降低0.102cm。
因此在容器外壁每隔1.02cm标记一次刻度,这样水面每降低一个刻度,就代表时间经过了10分钟.
方法总结:(1)正确理解题意,建立一次函数模型;
(2)结合图象,抓住关键点信息,分析条件,确定函数关系
(3)将数据转化为点坐标,利用待定系数法确定函数表达式;
(4)正确理解并应用一次函数中系数K、b的含义
模块二:反比例函数应用题
例题精讲
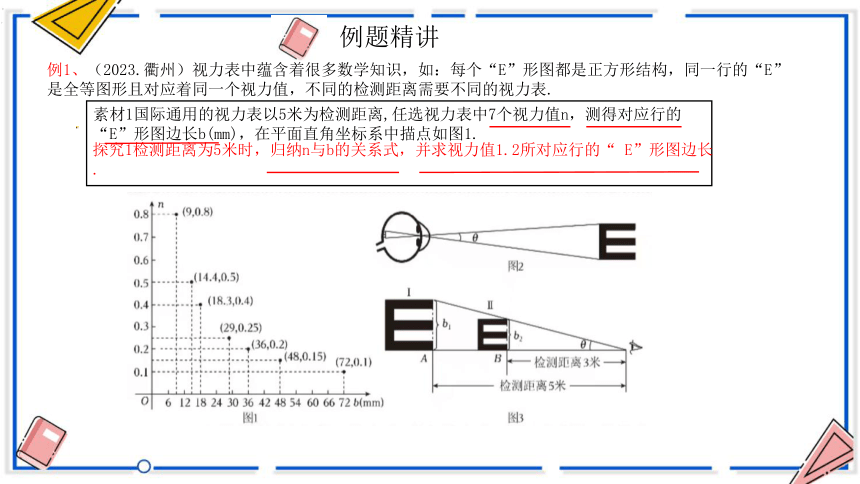
例1、(2023.衢州)视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“ E”形图边长.
例题精讲
例1、
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“ E”形图边;
待定系数法
解:探究1:
由图象中的点的坐标规律得到n与b成反比例关系,
设n= (k≠0),将其中一点(9,0.8)代入得: 0.8=
解得: k=7.2,
n= ,将其余各点一一代入验证,都符合关系式;
答:检测距离为5米时,视力值1.2所对应行
的“E”形图边长为6mm;
将n=1.2代入n=
得: b=6
例题精讲
例1、视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着
同一个视力值,不同的检测距离需要不同的视力表.
素材2图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“E”形图所成的角叫做分辨视角θ,视力值n与分辨视角θ(分)的对应关系近似满足n=1θ(0.5≤θ≤10).
探究2当n≥1.0时,属于正常视力,根据函数增减性写出对应的分辨视角θ范围;
?
解:探究2:
∵n=
在自变量θ的取值范围内,n随着θ的增大而减小,
当n≥1.0时,0<θ≤1.0,
又∵0.5≤θ
≤10,
0.5≤θ
≤1.0;
例题精讲
例1、视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着
同一个视力值,不同的检测距离需要不同的视力表.
素材3如图3,当θ确定时,在A处用边长为b1的I号“E”测得的视力与在B处用边长为 b?的Ⅱ号“E”测得的视力相同.
探究3若检测距离为3米,求视力值1.2所对应行的“E”形图边长.
?
探究3:由素材可知,当某人的视力确定时,其分辨视角也是
确定的,由相似三角形性质可得
由探究1知b1=6,
解得b2=3.6
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为3.6mm.
例题精讲
例2、建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性
近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑
更多的创意和流动性.图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH
(反比例函数图象的一支)和若干线段围成,其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,
AC=20m,GM=10m,MN=4m,如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角
坐标系.请回答下列问题:
(1)如图2,求EG所在双曲线的解析式.
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ
用来雕刻EG所在曲面的花纹,请问点P在EG上滑动过程中,PQ最长为多少米?
(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,
请求出此时线段HN上光线无法直射部分即线段KN的长.
例题精讲
例2、双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH(反比例函数图象的一支)和若干线段围成,
其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,AC=20m,GM=10m,MN=4m,
如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.请回答下列问题:
(1)如图2,求EG所在双曲线的解析式.
2
2
-10
解:(1)∵AB=2m,BE=2m,AC=20m,
O为AC中点,AO=10m,
∴E(﹣8,﹣2)
-8
设EG所在双曲线的表达式为
将点E坐标(﹣8,﹣2)代入表达式中,
得:
解得k=16,
∴双曲线的表达式为
-2
例题精讲
例2、双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH(反比例函数图象的一支)和若干线段围成,
其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,AC=20m,GM=10m,MN=4m,
如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.请回答下列问题:
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ
用来雕刻EG所在曲面的花纹,请问点P在EG上滑动过程中,PQ最长为多少米?
解:(2)如图:点E与点G坐标分别为(﹣8,﹣2),(﹣2,﹣8),
设EG所在直线解析式y=k1x+b1,将E、G两点坐标代入得
∴EG所在直线解析式为y=﹣x﹣10,
y=x
解得:
根据反比例函数图象轴对称的性质,曲线EG关于直线y=x对称
又PQ EG ,因此当P、Q分别为线段EG、曲线EG与直线y=x的交点时,PQ最长
∴PQ的最大值为
例题精讲
例2、(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,
请求出此时线段HN上光线无法直射部分即线段KN的长.
T
解:(3)如图,光线与曲线EG相切于T,设直线AE的解析式为 y=k2x+b2
将点A(﹣10,0),点E(﹣8,﹣2)代入得
解得:
∴AE所在直线解析式为y=﹣x﹣10,
∵TK∥AE,设直线TK解析式为y=﹣x+m,曲线EG相切于T
解得m=﹣8或m=8(舍)
∴TK解析式为y=﹣x﹣8,
将x=2分别代入y=﹣x﹣8,
解得点K(2,﹣10),点G(﹣2,﹣8)
又∵点M(﹣2,﹣18)点N(2,﹣18),
∴KN=﹣10﹣(﹣18)=8.
10
-2
2
(-2,-8)
(-2,-18)
(2,-18)
(2, )
?
√
反比例函数应用题总结:
根据具体情境分析确定反比例函数关系模型,根据已知条件确定
表达式
②联立两个函数表达式得方程组求交点坐标
③一次函数和反比例函数相切问题对应联立两个函数表达式,将图像的特殊位置关系对应转化为 一元二次方程判别式等于0的情况进一步求解
模块三:二次函数应用题
例题精讲
例1、深圳地铁16号线(ShenzhenMetroLine16),又称“深圳地铁龙坪线”,是深圳市境内第16条建成运营的地铁线路,于2022年12月28日开通运营一期工程(大运站至田心站)。数学小组成员了解到16号线地铁进入某站时在距离停车线400米处开始减速.他们想了解地铁从减速开始,经过多少秒在停车线
处停下?为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的函数关系,再应用该函数解决相应问题.
(1)【建立模型】 ①收集数据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t(秒)
0
4
8
12
16
20
24
28
…
S(米)
400
324
256
196
144
100
64
36
…
②绘制图像:
在平面直角坐标系中描出所收集数据对应的点,
并用光滑的曲线依次连接
例题精讲
③猜想模型:观察这条曲线的形状,它可能是 函数的图象.(请填写选项)
A.一次 B. 二次 C.反比例
④求解析式:请根据表格数据,求出S关于t的解析式(自变量t的取值范围不作要求)待定系数法
⑤验证结论:将数据中的其余几对值代入所求的解析式,发现他们 (“都”或“不都”)满足该函数解析式。
解: (1)、③根据图象可得:观察这条曲线的形状,它可能是二次函数的图象,故答案为:B;
④设函数为s = at?+ bt +c (a≠0)
把(0,400),(4,324),(8,256)代入s = at?+ bt +c可得:
解得:
S关于t的解析式为:
⑤将数据中的其余几对值代入所求的解析式,
发现他们满足该函数解析式
例题精讲
例1、数学小组成员了解到16号线地铁进入某站时在距离停车线400米处开始减速.他们想了解地铁从减速 开始,经过多少秒在停车线处停下?为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的函数关系,再应用该函数解决相应问题.
(2)【问题解决】:地铁从减速开始,经过 秒在停车线处停下。
(2)解:由(1)中的第④小问已经确定了s=14t?-20t+400,
?
因此令s=0得: 0=14t?-20t+400,
解得t1=t2=40,
?
地铁从减速开始,经过40秒在停车线处停下
例题精讲
例1、为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的
函数关系,再应用该函数解决相应问题.
(3)【拓展应用】:已知16号地铁列车在该地铁站经历的过程如下:进站:车头从进站那一刻起到停车线处停下,
用时24秒;停靠:列车停靠时长为40秒(即列车停稳到再次启动停留的时间为40秒);出站:列车再次启动到
列车车头刚好出站,用时5秒。数学小组经计算得知,在地铁列车出站过程中,列车车头离停车线的距离
s(米)与时间t(秒)的函数关系变为s =12(t -80)?(80 ≤t≤100),请结合函数图象,求出该地铁站的长度是 米.
?
解:(3)由题意可得:地铁从减速开始,经过40秒在停车线处停下,车头从进站那一刻起到停车线处停下用时24秒,
当t= 16时,s=144,此时站内长度为144米,
在地铁列车出站过程中,列车车头离停车线的距离s米与时间t(秒)的函数关系变为:
当t = 85时,整个站的长度为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t(秒)
0
4
8
12
16
20
24
28
…
S(米)
400
324
256
196
144
100
64
36
…
t=16
t=40
144米
12.5米
144+12.5=156.5(米)
故该地铁站的长度156.5米.
例题精讲
例2、(2023.贵州)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在OC上找一点P,加装拉杆PA,PB,同时使拉杆的长度之和最短,请你帮小星找到点P的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(1)求抛物线的表达式;
解:(1)设抛物线的解析式为y=ax2+9,
把点A(3,0)代入,得:9a+9=0,
解得:a=﹣1,
∴抛物线的解析式为:y=﹣x2+9;
(0,9)
(3,0)
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
解:(2)作A点关于y轴的对称点A′(﹣3,0),
连接A′B交OC于点P,则P点即为所求;
把x=1代入y=﹣x2+9,得:y=8,
∴B(1,8)
设直线A′B的解析式为y=kx+m,将A′(﹣3,0)B(1,8)代入得:
∴y=2x+6
(2)如图②,为更加稳固,小星想在OC上找一点P,加装拉杆PA,PB,同时使拉杆的长度之和最短,
请你帮小星找到点P的位置并求出坐标;
A′
P
将军饮马问题
令x=0,得y=6,∴P点的坐标为(0,6);
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(3)y=﹣x2+2bx+b﹣1=﹣(x﹣b)2+b2+b﹣1,
∴抛物线的对称轴为直线x=b,顶点坐标为(b,b2+b﹣1),
(I)当0<b≤4时,当4≤x≤6时, x=6时,y=﹣62+12b+b﹣1为最小值
得:﹣62+12b+b﹣1≥9,解得:
≤b≤4,
∴
2
4
6
o
y
x
直线x=b
(6,﹣62+12b+b﹣1)
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(II)当4<b<6时,又分两种情况:
情况一: 当b﹣4≤6﹣b,得:b≤5,
如图,当4≤x≤6,x=6时,y=﹣62+12b+b﹣1为最小值
∴﹣62+12b+b﹣1≥9,解得:
∴4<b≤5;
2
4
6
o
y
x
直线x=b
(6,﹣62+12b+b﹣1)
5
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(II)当4<b<6时,
情况二: 当b﹣4>6﹣b,得:b>5,
如图,当4≤x≤6,x=4时,y=﹣42+8b+b﹣1为最小值
∴﹣42+8b+b﹣1≥9,解得:
∴5<b<6;
2
4
6
o
y
x
直线x=b
(4,﹣42+8b+b﹣1)
5
综合情况一、二 得:
4<b<6,当4≤x≤6时,函数y的值总大于等于9都成立;
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(III)当b≥6时,如图
当4≤x≤6,x=4时,y=﹣42+8b+b﹣1为最小值
∴﹣42+8b+b﹣1≥9,解得:
∴b≥6;
2
4
6
o
y
x
直线x=b
(4,﹣42+8b+b﹣1)
综合情况(I)、(II)、(III) 得:
b的取值范围为 时,当4≤x≤6时,函数y的值总大于等于9都成立;
第十三讲
一、二次函数与反比例函数应用题
罗湖外语初中学校 任平
模块一:一次函数应用题
1、结合具体情境体会一次函数的意义,能根据已知条件(文字、图象、表格)
分析函数关系;会运用待定系数法确定一次函数的表达式
2、能画一次函数的图象,根据图象和表达式y=kx +b(k 0)探索并理解k>0
和k<0时图象的变化情况
3、体会一次函数与二元一次方程的关系
4、能用一次函数解决简单实际问题
实际问题
函数模型
分析模型、结合模型对数学问题求解
例题精讲
例1(2020.绍兴)我国传统的计重工具—秤的应用,方便了人们的生活。如图1,可以用秤砣到秤纽的水平距离来得出秤钩上所挂物体的重量。称重时,若秤杆上秤砣到秤纽的水平距离为x (厘米)时,秤钩所挂物重为y(斤),则y是x的一次函数。下表中为若干次称重时所记录的一些数据。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
(1)在上表x, y的数据中,发现有一对数据记录错误,
在图2中,通过描点的方法,观察判断哪一对数据是错误的?
(2) 根据(1)的发现,问秤杆上秤砣到秤纽的
水平距离为16厘米时,秤钩所挂物重是多少?
例题精讲
因为y是x的一次函数,所以函数图象为一条直线
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
解:(1)在坐标系中描点,连线
观察图象可知:
这组数据有错误
例题精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
1
2
4
7
11
12
0.75
1.00
1.50
2.75
3.25
3.50
解:
(2) 根据(1)的发现,问秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少?
答:秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤.
例题精讲
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日期
销售记录
6月1日
库存600kg ,成本价8元/kg ,售价10元/ kg(除了促销降价,其他时间售价保持不变)
6月9日
从6月1日至今,一共售出200kg
6月10、11日
这两天以成本价促销,之后售价恢复到10元/kg
6月12日
补充进货200kg ,成本价8.5元/kg
6月30日
800kg水果全部售完,一共获利1200元.
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
解:
(元)
答:截止到6月9日,该商店销售这种水果一共获利400元.
例2、(2020.苏州)某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
例题精讲
例2、(2020.苏州)某商店代理销售一种水果,六月份的销售利润y(元)与销售量x(kg)之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}日期
销售记录
6月1日
库存600kg ,成本价8元/kg ,售价10元/ kg(除了促销降价,其他时间售价保持不变)
6月9日
从6月1日至今,一共售出200kg
6月10、11日
这两天中先以成本价促销,之后售价恢复到10元/kg到该批水果卖完
6月12日
补充进货200kg ,成本价8.5元/kg
6月30日
800kg水果全部售完,一共获利1200元.
(2)求图像中线段BC所在直线对应的函数表达式.
(800,1200)
促销期间利润不增加
(a,400)
解:设点B的坐标为(a,400),依题意得
解得:
∴点B的坐标为(350,400)
待定系数法
促销卖掉(a-200)kg
[600-(a-200)]×(10-8)
+200×(10-8.5)=1200
设线段BC所在直线的函数表达式为y=kx+b(k≠0)
将B(350,400)、C(800,1200)两点坐标分别代入表达式得
.
∴线段BC所在直线的函数表达式为
例题精讲
例3、(2023.台州)【问题背景】“刻漏”是我国古代的一种利用水流计时的工具.综合实践小组准备用甲
乙两个透明的竖直放置的容器和一根带节流阀(控制水的流速大小)的软管制作简易计时装置.
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始
放水后每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【建立模型】小组讨论发现:“t=0,h=30”是初始状态下的准确数据,
水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
任务1:分别计算表中每隔10min水面高度观察值的变化量
任务2:利用t=0时,h=30;t=10时,h=29这两组数据求水面高度h与流水时间t的函数解析式;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
解:任务1:变化量分别为:
29﹣30=﹣1(cm);28.1﹣29=﹣0.9(cm);
27﹣28.1=﹣1.1(cm);25.8﹣27=﹣1.2(cm)
∴每隔10min水面高度观察值的变化量为:
﹣1,﹣0.9,﹣1.1,﹣1.2.
任务2:设水面高度h与流水时间t的函数解析式为
h=kt+b
∵t=0 时,h=30;t=10时,h=29;代入表达式得
∴水面高度h与流水时间t的函数解析式为h=﹣0.1t+30;
解得
例题精讲
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后
每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【反思优化】经检验,发现有两组表中观察值不满足任务2中求出的函数解析式,
存在偏差,小组决定优化函数解析式,减少偏差.通过查阅资料后知道:
t为表中数据时,根据解析式求出所对应的函数值,计算这些函数值与
对应h的观察值之差的平方和,记为w;w越小,偏差越小.
任务3:(1)计算任务2得到的函数解析式的w值;
(2)请确定经过(0,30)的一次函数解析式,使得w的值最小;
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
任务2得到h=﹣0.1t+30
任务3:
(1)w=(30﹣30)?+(29﹣29)2+(28﹣28.1)2+(27﹣27)2+(26﹣25.8)2=0.05.
(2)设优化后的函数表达式为 h=mt+30,
w=(0+30﹣30)2+(10m+30﹣29)2+(20m+30﹣28.1)2+(30m+30﹣27)2+(40m+30﹣25.8)2
=3000(m+0.102)2+0.038
∵ 3000>0,函数开口向上,∴当m=﹣0.102时,w的最小值为0.038. 此时h=-0.102t+30
例题精讲
【实验操作】综合实践小组设计了如下的实验:先在甲容器里加满水,此时水面高度为30cm,开始放水后
每隔10min观察一次甲容器中的水面高度,获得的数据如表:
【设计刻度】得到优化的函数解析式后,综合实践小组决定在甲容器外壁设计刻度,
通过刻度直接读取时间.
任务4:请你简要写出时间刻度的设计方案.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}流水时间t/min
0
10
20
30
40
水面高度h/cm(观察值)
30
29
28.1
27
25.8
解:任务4:由任务3可知优化之后的函数关系式为:h= ﹣0.102 t+30 .即每分钟水位降低0.102cm。
因此在容器外壁每隔1.02cm标记一次刻度,这样水面每降低一个刻度,就代表时间经过了10分钟.
方法总结:(1)正确理解题意,建立一次函数模型;
(2)结合图象,抓住关键点信息,分析条件,确定函数关系
(3)将数据转化为点坐标,利用待定系数法确定函数表达式;
(4)正确理解并应用一次函数中系数K、b的含义
模块二:反比例函数应用题
例题精讲
例1、(2023.衢州)视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“ E”形图边长.
例题精讲
例1、
素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“E”形图边长b(mm),在平面直角坐标系中描点如图1.
探究1检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“ E”形图边;
待定系数法
解:探究1:
由图象中的点的坐标规律得到n与b成反比例关系,
设n= (k≠0),将其中一点(9,0.8)代入得: 0.8=
解得: k=7.2,
n= ,将其余各点一一代入验证,都符合关系式;
答:检测距离为5米时,视力值1.2所对应行
的“E”形图边长为6mm;
将n=1.2代入n=
得: b=6
例题精讲
例1、视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着
同一个视力值,不同的检测距离需要不同的视力表.
素材2图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“E”形图所成的角叫做分辨视角θ,视力值n与分辨视角θ(分)的对应关系近似满足n=1θ(0.5≤θ≤10).
探究2当n≥1.0时,属于正常视力,根据函数增减性写出对应的分辨视角θ范围;
?
解:探究2:
∵n=
在自变量θ的取值范围内,n随着θ的增大而减小,
当n≥1.0时,0<θ≤1.0,
又∵0.5≤θ
≤10,
0.5≤θ
≤1.0;
例题精讲
例1、视力表中蕴含着很多数学知识,如:每个“E”形图都是正方形结构,同一行的“E”是全等图形且对应着
同一个视力值,不同的检测距离需要不同的视力表.
素材3如图3,当θ确定时,在A处用边长为b1的I号“E”测得的视力与在B处用边长为 b?的Ⅱ号“E”测得的视力相同.
探究3若检测距离为3米,求视力值1.2所对应行的“E”形图边长.
?
探究3:由素材可知,当某人的视力确定时,其分辨视角也是
确定的,由相似三角形性质可得
由探究1知b1=6,
解得b2=3.6
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为3.6mm.
例题精讲
例2、建筑是一门不断演化和创新的艺术,从古代的大理石殿堂到现代的钢铁森林,它的魅力在于其无限的可能性
近年来,一种名为双曲铝单板的新兴材料以其独特的曲线和光泽,为建筑注入了新的时尚元素,同时也赋予了建筑
更多的创意和流动性.图2为某广东厂家设计制造的双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH
(反比例函数图象的一支)和若干线段围成,其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,
AC=20m,GM=10m,MN=4m,如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角
坐标系.请回答下列问题:
(1)如图2,求EG所在双曲线的解析式.
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ
用来雕刻EG所在曲面的花纹,请问点P在EG上滑动过程中,PQ最长为多少米?
(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,
请求出此时线段HN上光线无法直射部分即线段KN的长.
例题精讲
例2、双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH(反比例函数图象的一支)和若干线段围成,
其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,AC=20m,GM=10m,MN=4m,
如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.请回答下列问题:
(1)如图2,求EG所在双曲线的解析式.
2
2
-10
解:(1)∵AB=2m,BE=2m,AC=20m,
O为AC中点,AO=10m,
∴E(﹣8,﹣2)
-8
设EG所在双曲线的表达式为
将点E坐标(﹣8,﹣2)代入表达式中,
得:
解得k=16,
∴双曲线的表达式为
-2
例题精讲
例2、双曲铝单板建筑的横截面,可以看作由两条曲线EG、FH(反比例函数图象的一支)和若干线段围成,
其中四边形ABDC与四边形GMNH均为矩形,AB=2m,BE=2m,AC=20m,GM=10m,MN=4m,
如图2所示,取AC中点O,以点O为原点,AC所在直线为x轴建立平面直角坐标系.请回答下列问题:
(2)如图3,为在曲面实现自动化操作,工程师安装了支架EG,并加装了始终垂直于EG的伸缩机械臂PQ
用来雕刻EG所在曲面的花纹,请问点P在EG上滑动过程中,PQ最长为多少米?
解:(2)如图:点E与点G坐标分别为(﹣8,﹣2),(﹣2,﹣8),
设EG所在直线解析式y=k1x+b1,将E、G两点坐标代入得
∴EG所在直线解析式为y=﹣x﹣10,
y=x
解得:
根据反比例函数图象轴对称的性质,曲线EG关于直线y=x对称
又PQ EG ,因此当P、Q分别为线段EG、曲线EG与直线y=x的交点时,PQ最长
∴PQ的最大值为
例题精讲
例2、(3)如图4,为通风透气避免潮湿,在某一时刻,打开遮光板AC,太阳光线经点A恰好照射到点E,
请求出此时线段HN上光线无法直射部分即线段KN的长.
T
解:(3)如图,光线与曲线EG相切于T,设直线AE的解析式为 y=k2x+b2
将点A(﹣10,0),点E(﹣8,﹣2)代入得
解得:
∴AE所在直线解析式为y=﹣x﹣10,
∵TK∥AE,设直线TK解析式为y=﹣x+m,曲线EG相切于T
解得m=﹣8或m=8(舍)
∴TK解析式为y=﹣x﹣8,
将x=2分别代入y=﹣x﹣8,
解得点K(2,﹣10),点G(﹣2,﹣8)
又∵点M(﹣2,﹣18)点N(2,﹣18),
∴KN=﹣10﹣(﹣18)=8.
10
-2
2
(-2,-8)
(-2,-18)
(2,-18)
(2, )
?
√
反比例函数应用题总结:
根据具体情境分析确定反比例函数关系模型,根据已知条件确定
表达式
②联立两个函数表达式得方程组求交点坐标
③一次函数和反比例函数相切问题对应联立两个函数表达式,将图像的特殊位置关系对应转化为 一元二次方程判别式等于0的情况进一步求解
模块三:二次函数应用题
例题精讲
例1、深圳地铁16号线(ShenzhenMetroLine16),又称“深圳地铁龙坪线”,是深圳市境内第16条建成运营的地铁线路,于2022年12月28日开通运营一期工程(大运站至田心站)。数学小组成员了解到16号线地铁进入某站时在距离停车线400米处开始减速.他们想了解地铁从减速开始,经过多少秒在停车线
处停下?为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的函数关系,再应用该函数解决相应问题.
(1)【建立模型】 ①收集数据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t(秒)
0
4
8
12
16
20
24
28
…
S(米)
400
324
256
196
144
100
64
36
…
②绘制图像:
在平面直角坐标系中描出所收集数据对应的点,
并用光滑的曲线依次连接
例题精讲
③猜想模型:观察这条曲线的形状,它可能是 函数的图象.(请填写选项)
A.一次 B. 二次 C.反比例
④求解析式:请根据表格数据,求出S关于t的解析式(自变量t的取值范围不作要求)待定系数法
⑤验证结论:将数据中的其余几对值代入所求的解析式,发现他们 (“都”或“不都”)满足该函数解析式。
解: (1)、③根据图象可得:观察这条曲线的形状,它可能是二次函数的图象,故答案为:B;
④设函数为s = at?+ bt +c (a≠0)
把(0,400),(4,324),(8,256)代入s = at?+ bt +c可得:
解得:
S关于t的解析式为:
⑤将数据中的其余几对值代入所求的解析式,
发现他们满足该函数解析式
例题精讲
例1、数学小组成员了解到16号线地铁进入某站时在距离停车线400米处开始减速.他们想了解地铁从减速 开始,经过多少秒在停车线处停下?为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的函数关系,再应用该函数解决相应问题.
(2)【问题解决】:地铁从减速开始,经过 秒在停车线处停下。
(2)解:由(1)中的第④小问已经确定了s=14t?-20t+400,
?
因此令s=0得: 0=14t?-20t+400,
解得t1=t2=40,
?
地铁从减速开始,经过40秒在停车线处停下
例题精讲
例1、为解决这一问题,数学小组建立函数模型来描述地铁列车车头离停车线的距离s(米)与时间t(秒)的
函数关系,再应用该函数解决相应问题.
(3)【拓展应用】:已知16号地铁列车在该地铁站经历的过程如下:进站:车头从进站那一刻起到停车线处停下,
用时24秒;停靠:列车停靠时长为40秒(即列车停稳到再次启动停留的时间为40秒);出站:列车再次启动到
列车车头刚好出站,用时5秒。数学小组经计算得知,在地铁列车出站过程中,列车车头离停车线的距离
s(米)与时间t(秒)的函数关系变为s =12(t -80)?(80 ≤t≤100),请结合函数图象,求出该地铁站的长度是 米.
?
解:(3)由题意可得:地铁从减速开始,经过40秒在停车线处停下,车头从进站那一刻起到停车线处停下用时24秒,
当t= 16时,s=144,此时站内长度为144米,
在地铁列车出站过程中,列车车头离停车线的距离s米与时间t(秒)的函数关系变为:
当t = 85时,整个站的长度为:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t(秒)
0
4
8
12
16
20
24
28
…
S(米)
400
324
256
196
144
100
64
36
…
t=16
t=40
144米
12.5米
144+12.5=156.5(米)
故该地铁站的长度156.5米.
例题精讲
例2、(2023.贵州)如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图②,为更加稳固,小星想在OC上找一点P,加装拉杆PA,PB,同时使拉杆的长度之和最短,请你帮小星找到点P的位置并求出坐标;
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(1)求抛物线的表达式;
解:(1)设抛物线的解析式为y=ax2+9,
把点A(3,0)代入,得:9a+9=0,
解得:a=﹣1,
∴抛物线的解析式为:y=﹣x2+9;
(0,9)
(3,0)
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
解:(2)作A点关于y轴的对称点A′(﹣3,0),
连接A′B交OC于点P,则P点即为所求;
把x=1代入y=﹣x2+9,得:y=8,
∴B(1,8)
设直线A′B的解析式为y=kx+m,将A′(﹣3,0)B(1,8)代入得:
∴y=2x+6
(2)如图②,为更加稳固,小星想在OC上找一点P,加装拉杆PA,PB,同时使拉杆的长度之和最短,
请你帮小星找到点P的位置并求出坐标;
A′
P
将军饮马问题
令x=0,得y=6,∴P点的坐标为(0,6);
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(3)y=﹣x2+2bx+b﹣1=﹣(x﹣b)2+b2+b﹣1,
∴抛物线的对称轴为直线x=b,顶点坐标为(b,b2+b﹣1),
(I)当0<b≤4时,当4≤x≤6时, x=6时,y=﹣62+12b+b﹣1为最小值
得:﹣62+12b+b﹣1≥9,解得:
≤b≤4,
∴
2
4
6
o
y
x
直线x=b
(6,﹣62+12b+b﹣1)
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(II)当4<b<6时,又分两种情况:
情况一: 当b﹣4≤6﹣b,得:b≤5,
如图,当4≤x≤6,x=6时,y=﹣62+12b+b﹣1为最小值
∴﹣62+12b+b﹣1≥9,解得:
∴4<b≤5;
2
4
6
o
y
x
直线x=b
(6,﹣62+12b+b﹣1)
5
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(II)当4<b<6时,
情况二: 当b﹣4>6﹣b,得:b>5,
如图,当4≤x≤6,x=4时,y=﹣42+8b+b﹣1为最小值
∴﹣42+8b+b﹣1≥9,解得:
∴5<b<6;
2
4
6
o
y
x
直线x=b
(4,﹣42+8b+b﹣1)
5
综合情况一、二 得:
4<b<6,当4≤x≤6时,函数y的值总大于等于9都成立;
例题精讲
例2、如图①,是一座抛物线型拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图
是抛物线的一部分(如图②所示),抛物线的顶点在C处,对称轴OC与水平线OA垂直,OC=9,点A在
抛物线上,且点A到对称轴的距离OA=3,点B在抛物线上,点B到对称轴的距离是1.
(3)为了造型更加美观,小星重新设计抛物线,其表达式为y=﹣x2+2bx+b﹣1(b>0),
当4≤x≤6时,函数y的值总大于等于9.求b的取值范围.
解:(III)当b≥6时,如图
当4≤x≤6,x=4时,y=﹣42+8b+b﹣1为最小值
∴﹣42+8b+b﹣1≥9,解得:
∴b≥6;
2
4
6
o
y
x
直线x=b
(4,﹣42+8b+b﹣1)
综合情况(I)、(II)、(III) 得:
b的取值范围为 时,当4≤x≤6时,函数y的值总大于等于9都成立;
同课章节目录
