深圳市中考备考百师助学培优课程——第8讲:用平行线解函数中三角形面积问题 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第8讲:用平行线解函数中三角形面积问题 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 485.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
利用平行线解决函数中的
三角形面积问题
罗湖区中考备考“百师助学”课程第八讲
罗湖外语初中学校 黄永稳
1.利用平行线转换三角形面积,进而解决问题;
2.体会数学中的数形结合思想、转化思想等,提高综合解决问题能力。
学习目标
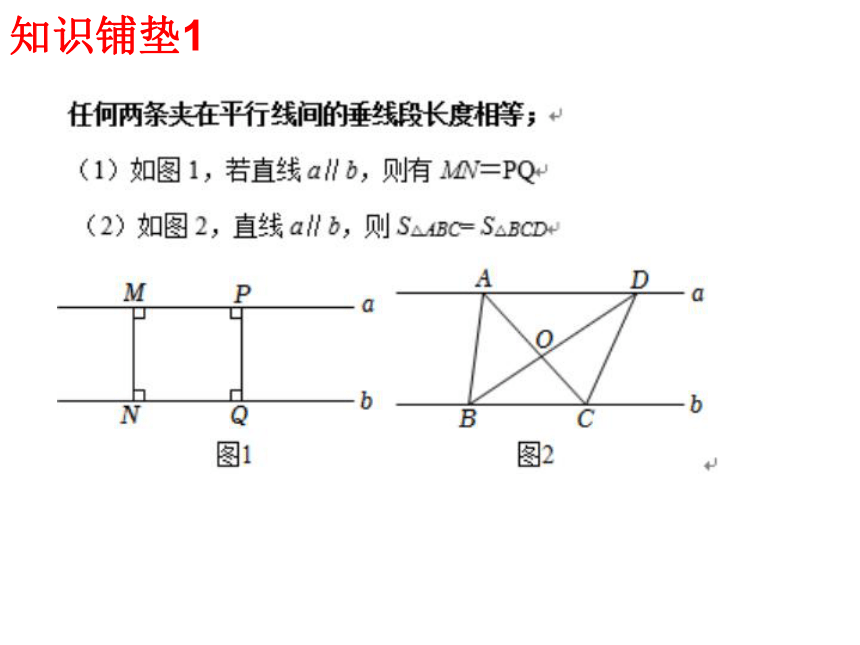
知识铺垫1
知识铺垫1
知识铺垫2
b1
b2
y=kx+b1
y=kx
y=kx+b2
一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行则可以推出k1=k2
反之若k1=k2则可推出一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行,其中b1≠b2.
模块一 利用平行转换面积
例题精讲:1. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A(0,4).与x轴交于点B(-2,0)和点C(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
H
解题思路:
1、连接MC,∵NM∥AC,∴S△AMN=S△CMN
把S△AMN转化为S△CMN
2、作OH⊥于x轴交于点H,设未知数表示CN、
MH的长。
3、列方程、解方程、作答
模块一 利用平行转换面积
例题精讲:1. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A(0,4).与x轴交于点B(-2,0)和点C(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
H
解:连接MC,作MH⊥BC交BC于点H,设NC=m,
∵B(-2,0),C(8,0)∴BC=10
∵MN∥AC,∴∠MNB=∠ACB,∠MBN=∠ABC
∴
模块一 利用平行转换面积
学生练习:1、已知:如图,抛物线y=x2+4x+3交x轴于E、F 两点,交y轴于A点,若Q为抛物线上一点,连接QE,QA,设点Q 的横坐标为t(t<﹣3),△QAE的面积为S,求S与t函数关系式;
P
点拨:过点Q作PQ∥AE交y轴于点P,连接PE。则S△QAE=S△PAE
模块二:同底三角形面积比问题
典例精讲:例1、如图,在平面直角坐标系中,抛物线
y=-x2+2x+3与交x轴于点A,与y轴交于点C.点M的坐标为(4,-5),在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等(即S△PMC:S△AMC=1:1)?若存在,直接写出点P的坐标;若不存在,请说明理由.
解题思路:
1、求出A、C坐标和直线MC表达式
2、过点A作AB∥MC,利用直线MC的k值和点A坐标求出直线AB的表达式
3、分情况讨论:a、当点P在AC的上方时,联立直线AB表达式和二次函数组成方程组,求出两函数交点P的坐标。
4、分情况讨论:b、当点P在AC的下方时利用平移表示出点P所在的直线,联立二次函数进而解决点P的坐标。
P1
B(0,6)
P2
P3
Q
E
F
P1
B(0,6)
P2
P3
解:当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),当x=0时,y=﹣x2+2x+3=3,则C(0,3)
设直线CM的解析式为y=mx+n,
把C(0,3),M(4,﹣5)代入得m=﹣2,n=3,
∴直线MC的解析式为y=﹣2x+3,
∵△PMC的面积与△AMC的面积相等,
∴AP∥MC,
设AP的解析式为y=﹣2x+p,
把A(3,0)代入得p=6,
∴AP的解析式为y=﹣2x+6,
解方程组
得
或
∴此时P点坐标为(1,4)
直线AP的解析式为y=﹣2x+6与y轴的交点坐标为(0,6),
∵6﹣3=3,
把直线CM向下平移3个单位得到y=﹣2x,
得
或
解方程
模块二:同底三角形面积比问题
典例精讲:例2. 如图,抛物线y=﹣ x2+3x+8与x轴交于点A、B点,与y轴交于点C点,P是抛物线上第一象限上的动点,连接PB,PC,
当 时,求点P的坐标.
D
M
N
E
P1
P2
解题思路:
1、根据抛物线的表达式,求出点A、B、C的坐标以及BC的表达式。
2、过点A作AD平行于BC交y轴于点D,求出CD的长。
4、联立方程,求出点P的坐标
3、在y轴上点C的上方截取CE= CD,过点E作EP平行于CB
模块二:同底三角形面积比问题
D
M
N
E
P1
P2
解:把x=0和y=0分别代入二次函数表达式得
A(-2,0),B(8,0), C(0,8)
进而求得BC:y=﹣x+8
作AD//BC,交y轴于D,求得AD:y=﹣x-2,
∴点D(0,-2) CD=10,
在C点上方截取CE=6,过E作EP//BC,
交抛物线于点P,则P为所求的点
PE:y=﹣x+14,
联立方程组,
可得点P的坐标为P1(2,12)或P2(6,8)
模块三 利用相切解决面积最值问题
例题精讲1、如图,在平面直角坐标系内抛物线 与x轴交于点A,点B,与y轴交于点C.过点A的直线y=x+2与抛物线交于点E.点P为第四象限内抛物线上的一个动点.在点P的运动过程中,是否存在点P使得△AEP的面积最大,若存在,请求出点P的坐标.
解题思路:1、平移直线AE使得AE与抛物线相切,平移后的直线与抛物线的交点为P点,则此时△AEP的面积最大
2、联立方程,利用根的判别式求出P点坐标的横坐标,进而求出点P的坐标。
模块三 利用相切解决面积最值问题
M
N
模块三 利用相切解决面积最值问题
学生练习:2.如图,一次函数y=﹣x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A、B两点.点P在反比例函数第三象限的图象上,使得△PAB的面积最小,求满足条件的P点坐标及△PAB面积的最小值.
点拨:1、平移直线AB使得平移后的直线与第三象限的双曲线相切,平移后的直线与抛物线的交点则为P点,此时△PAB的面积最小
2、联立方程组,利用根的判别式求出平移后直线的表达式,进而求出点P的坐标。
P
二次函数面积问题
转移面积
课堂小结
面积比
转为水平线段比
转为铅垂线段比
面积最值
直线与曲线相切
转为边与x轴或y轴平行或重合的三角形的面积
祝同学们中考旗开得胜!!
利用平行线解决函数中的
三角形面积问题
罗湖区中考备考“百师助学”课程第八讲
罗湖外语初中学校 黄永稳
1.利用平行线转换三角形面积,进而解决问题;
2.体会数学中的数形结合思想、转化思想等,提高综合解决问题能力。
学习目标
知识铺垫1
知识铺垫1
知识铺垫2
b1
b2
y=kx+b1
y=kx
y=kx+b2
一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行则可以推出k1=k2
反之若k1=k2则可推出一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行,其中b1≠b2.
模块一 利用平行转换面积
例题精讲:1. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A(0,4).与x轴交于点B(-2,0)和点C(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
H
解题思路:
1、连接MC,∵NM∥AC,∴S△AMN=S△CMN
把S△AMN转化为S△CMN
2、作OH⊥于x轴交于点H,设未知数表示CN、
MH的长。
3、列方程、解方程、作答
模块一 利用平行转换面积
例题精讲:1. 如图,已知二次函数y=﹣ x2+ x+4的图象与y轴交于点A(0,4).与x轴交于点B(-2,0)和点C(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
H
解:连接MC,作MH⊥BC交BC于点H,设NC=m,
∵B(-2,0),C(8,0)∴BC=10
∵MN∥AC,∴∠MNB=∠ACB,∠MBN=∠ABC
∴
模块一 利用平行转换面积
学生练习:1、已知:如图,抛物线y=x2+4x+3交x轴于E、F 两点,交y轴于A点,若Q为抛物线上一点,连接QE,QA,设点Q 的横坐标为t(t<﹣3),△QAE的面积为S,求S与t函数关系式;
P
点拨:过点Q作PQ∥AE交y轴于点P,连接PE。则S△QAE=S△PAE
模块二:同底三角形面积比问题
典例精讲:例1、如图,在平面直角坐标系中,抛物线
y=-x2+2x+3与交x轴于点A,与y轴交于点C.点M的坐标为(4,-5),在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等(即S△PMC:S△AMC=1:1)?若存在,直接写出点P的坐标;若不存在,请说明理由.
解题思路:
1、求出A、C坐标和直线MC表达式
2、过点A作AB∥MC,利用直线MC的k值和点A坐标求出直线AB的表达式
3、分情况讨论:a、当点P在AC的上方时,联立直线AB表达式和二次函数组成方程组,求出两函数交点P的坐标。
4、分情况讨论:b、当点P在AC的下方时利用平移表示出点P所在的直线,联立二次函数进而解决点P的坐标。
P1
B(0,6)
P2
P3
Q
E
F
P1
B(0,6)
P2
P3
解:当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),当x=0时,y=﹣x2+2x+3=3,则C(0,3)
设直线CM的解析式为y=mx+n,
把C(0,3),M(4,﹣5)代入得m=﹣2,n=3,
∴直线MC的解析式为y=﹣2x+3,
∵△PMC的面积与△AMC的面积相等,
∴AP∥MC,
设AP的解析式为y=﹣2x+p,
把A(3,0)代入得p=6,
∴AP的解析式为y=﹣2x+6,
解方程组
得
或
∴此时P点坐标为(1,4)
直线AP的解析式为y=﹣2x+6与y轴的交点坐标为(0,6),
∵6﹣3=3,
把直线CM向下平移3个单位得到y=﹣2x,
得
或
解方程
模块二:同底三角形面积比问题
典例精讲:例2. 如图,抛物线y=﹣ x2+3x+8与x轴交于点A、B点,与y轴交于点C点,P是抛物线上第一象限上的动点,连接PB,PC,
当 时,求点P的坐标.
D
M
N
E
P1
P2
解题思路:
1、根据抛物线的表达式,求出点A、B、C的坐标以及BC的表达式。
2、过点A作AD平行于BC交y轴于点D,求出CD的长。
4、联立方程,求出点P的坐标
3、在y轴上点C的上方截取CE= CD,过点E作EP平行于CB
模块二:同底三角形面积比问题
D
M
N
E
P1
P2
解:把x=0和y=0分别代入二次函数表达式得
A(-2,0),B(8,0), C(0,8)
进而求得BC:y=﹣x+8
作AD//BC,交y轴于D,求得AD:y=﹣x-2,
∴点D(0,-2) CD=10,
在C点上方截取CE=6,过E作EP//BC,
交抛物线于点P,则P为所求的点
PE:y=﹣x+14,
联立方程组,
可得点P的坐标为P1(2,12)或P2(6,8)
模块三 利用相切解决面积最值问题
例题精讲1、如图,在平面直角坐标系内抛物线 与x轴交于点A,点B,与y轴交于点C.过点A的直线y=x+2与抛物线交于点E.点P为第四象限内抛物线上的一个动点.在点P的运动过程中,是否存在点P使得△AEP的面积最大,若存在,请求出点P的坐标.
解题思路:1、平移直线AE使得AE与抛物线相切,平移后的直线与抛物线的交点为P点,则此时△AEP的面积最大
2、联立方程,利用根的判别式求出P点坐标的横坐标,进而求出点P的坐标。
模块三 利用相切解决面积最值问题
M
N
模块三 利用相切解决面积最值问题
学生练习:2.如图,一次函数y=﹣x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A、B两点.点P在反比例函数第三象限的图象上,使得△PAB的面积最小,求满足条件的P点坐标及△PAB面积的最小值.
点拨:1、平移直线AB使得平移后的直线与第三象限的双曲线相切,平移后的直线与抛物线的交点则为P点,此时△PAB的面积最小
2、联立方程组,利用根的判别式求出平移后直线的表达式,进而求出点P的坐标。
P
二次函数面积问题
转移面积
课堂小结
面积比
转为水平线段比
转为铅垂线段比
面积最值
直线与曲线相切
转为边与x轴或y轴平行或重合的三角形的面积
祝同学们中考旗开得胜!!
同课章节目录
