深圳市中考备考百师助学培优课程——第5讲:《等腰三角形相关题型》模块二
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第5讲:《等腰三角形相关题型》模块二 |  | |
| 格式 | pptx | ||
| 文件大小 | 19.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 17:23:52 | ||
图片预览



文档简介
(共13张PPT)
《等腰三角形相关题型》
主讲人:段艳慈
模块二:等腰三角形的判定、等边三角形
重要知识回顾:等腰三角形的判定、等边三角形
01.
有两个角相等的三角形是等腰三角形。(等角对等边)
02.
等边三角形的三个内角都相等,并且每个角都是60°
03.
三个角都相等的三角形是等边三角形。
04.
有一个叫等于60°的等腰三角形是等边三角形。
模块二:典例精析
,
,
绕点A逆时针旋转后,得到
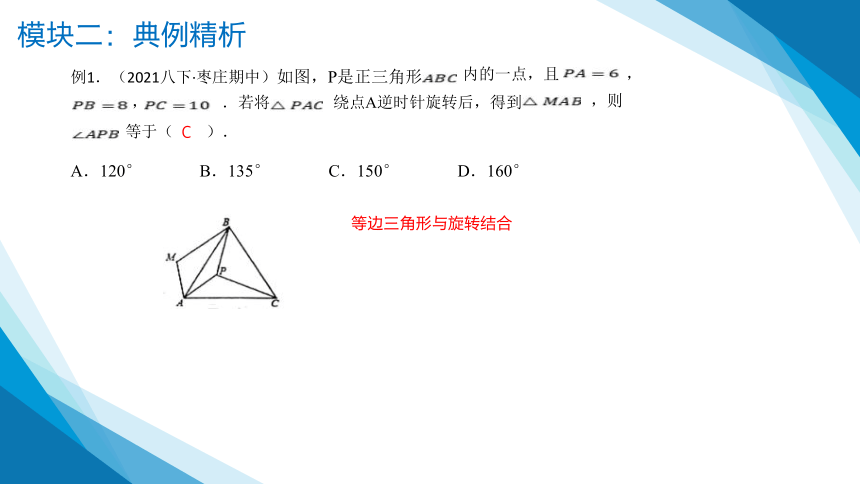
例1.(2021八下·枣庄期中)如图,P是正三角形
内的一点,且
.若将
,则
等于( ).
A.120° B.135° C.150° D.160°
等边三角形与旋转结合
C
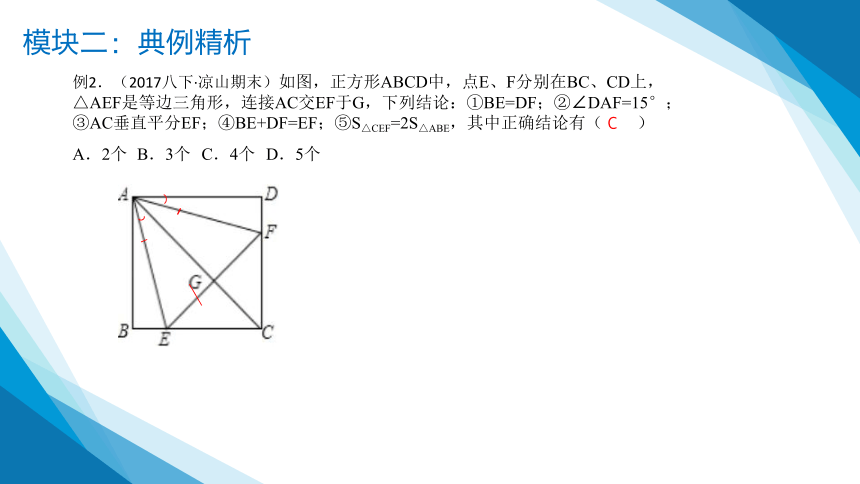
例2.(2017八下·凉山期末)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
模块二:典例精析
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
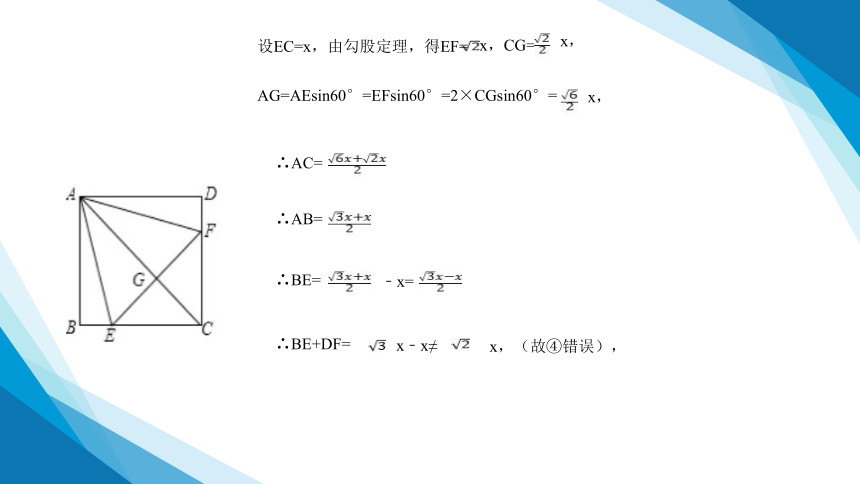
设EC=x,由勾股定理,得EF=
x,CG=
x,
x,
∴AB=
∴BE=
﹣x=
∴BE+DF=
x﹣x≠
x,(故④错误),
AG=AEsin60°=EFsin60°=2×CGsin60°=
∴AC=
例2.(2017八下·凉山期末)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
模块二:典例精析
C
conclusion
总结与归纳
the top "start" panel allows you to modify the font, size, color, line spacing, and more. it is recommended that the text be 8 to 18 characters with 1.3 times the space between the characters.
三、跟踪练习
1.如图,在7×7的正方形网格中,A,B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 个.
6
2.(2017·深圳模拟)如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D. 4个
3.(2019八下·九江期中)阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB= ;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
p
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
2
A1
O1
teaching
演示结束 谢谢观看
the top "start" panel allows you to modify the font, size, color, line spacing, and more. it is recommended that the text be 8 to 18 characters with 1.3 times the space between the characters.
授课人:段艳慈
教师说课│公开课│示范课│教师授课
《等腰三角形相关题型》
主讲人:段艳慈
模块二:等腰三角形的判定、等边三角形
重要知识回顾:等腰三角形的判定、等边三角形
01.
有两个角相等的三角形是等腰三角形。(等角对等边)
02.
等边三角形的三个内角都相等,并且每个角都是60°
03.
三个角都相等的三角形是等边三角形。
04.
有一个叫等于60°的等腰三角形是等边三角形。
模块二:典例精析
,
,
绕点A逆时针旋转后,得到
例1.(2021八下·枣庄期中)如图,P是正三角形
内的一点,且
.若将
,则
等于( ).
A.120° B.135° C.150° D.160°
等边三角形与旋转结合
C
例2.(2017八下·凉山期末)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
模块二:典例精析
Rt△ABE≌Rt△ADF(HL),
∴BE=DF(故①正确).
设EC=x,由勾股定理,得EF=
x,CG=
x,
x,
∴AB=
∴BE=
﹣x=
∴BE+DF=
x﹣x≠
x,(故④错误),
AG=AEsin60°=EFsin60°=2×CGsin60°=
∴AC=
例2.(2017八下·凉山期末)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
模块二:典例精析
C
conclusion
总结与归纳
the top "start" panel allows you to modify the font, size, color, line spacing, and more. it is recommended that the text be 8 to 18 characters with 1.3 times the space between the characters.
三、跟踪练习
1.如图,在7×7的正方形网格中,A,B两点是格点,如果点C也是格点,且△ABC是等腰三角形,这样的C点有 个.
6
2.(2017·深圳模拟)如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D. 4个
3.(2019八下·九江期中)阅读下面材料,并解决问题:
(1)如图①等边△ABC内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求∠APB的度数.
为了解决本题,我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′≌△ABP,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出∠APB= ;
(2)基本运用
请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2;
p
(3)能力提升
如图③,在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,点O为Rt△ABC内一点,连接AO,BO,CO,且∠AOC=∠COB=∠BOA=120°,求OA+OB+OC的值.
2
A1
O1
teaching
演示结束 谢谢观看
the top "start" panel allows you to modify the font, size, color, line spacing, and more. it is recommended that the text be 8 to 18 characters with 1.3 times the space between the characters.
授课人:段艳慈
教师说课│公开课│示范课│教师授课
同课章节目录
