深圳市中考备考百师助学培优课程——第4讲:《角平分线相关问题的应对策略》 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第4讲:《角平分线相关问题的应对策略》 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 624.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
角平分线的应对策略
模块一:角平分线邂逅平行线
桂园中学 余阳
角平分线的应对策略
模块二:角平分线性质定理推论——角平分线的比例问题
桂园中学 余阳
角平分线的应对策略
模块三:多角平分线问题——三角形内心的应用
桂园中学 余阳
三角形的内心
定义:三角形三条角平分线的交点。
三角形两条角平分线的交点。
性质:到三角形三边距离相等。
(与面积相关)
判定:到三角形三边距离相等的点是三角形的内心。
例1.(2020靖江市校级模拟)如图,在△4BC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的
平分线,与BC相交于点E,点G是BC上一点,E为线段BG的中点,DG⊥BC于点G,交AC于点F,
则FG的长为
G
E
A
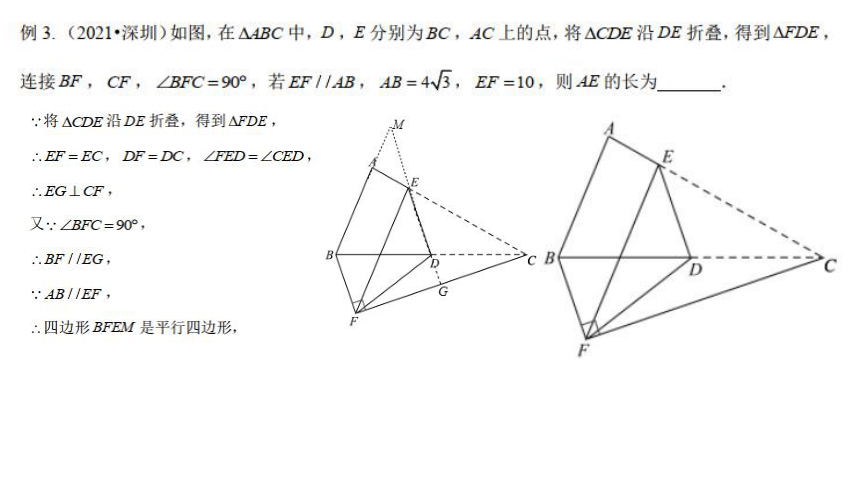
例3.(2021·深圳)如图,在△4BC中,D,E分别为BC,AC上的点,将△CDE沿DE折叠,得到△FDE,
连接BF,CF,BFC=90°,若EF/AB,AB=4V5,EF=10,则AE的长为
E
B
【解答】解:①四边形BCD是菱形,
.AB=BC=CD=AD,AB//CD
..∠B+∠BCD=180°,
.'∠BCD=120°,
.∠B=60°,
.△4BC,△ACD是等边三角形,
.∴.∠B=∠CAF=60°,
BE=AF,BC=AC,
.△BEC兰△4FC(S1S),正确:
角平分线的应对策略
模块一:角平分线邂逅平行线
桂园中学 余阳
角平分线的应对策略
模块二:角平分线性质定理推论——角平分线的比例问题
桂园中学 余阳
角平分线的应对策略
模块三:多角平分线问题——三角形内心的应用
桂园中学 余阳
三角形的内心
定义:三角形三条角平分线的交点。
三角形两条角平分线的交点。
性质:到三角形三边距离相等。
(与面积相关)
判定:到三角形三边距离相等的点是三角形的内心。
例1.(2020靖江市校级模拟)如图,在△4BC中,∠ABC=90°,且BC=6,AB=3,AD是∠BAC的
平分线,与BC相交于点E,点G是BC上一点,E为线段BG的中点,DG⊥BC于点G,交AC于点F,
则FG的长为
G
E
A
例3.(2021·深圳)如图,在△4BC中,D,E分别为BC,AC上的点,将△CDE沿DE折叠,得到△FDE,
连接BF,CF,BFC=90°,若EF/AB,AB=4V5,EF=10,则AE的长为
E
B
【解答】解:①四边形BCD是菱形,
.AB=BC=CD=AD,AB//CD
..∠B+∠BCD=180°,
.'∠BCD=120°,
.∠B=60°,
.△4BC,△ACD是等边三角形,
.∴.∠B=∠CAF=60°,
BE=AF,BC=AC,
.△BEC兰△4FC(S1S),正确:
同课章节目录
