深圳市中考备考百师助学培优课程——第14讲:手拉手模型常见结论的证明和应用 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第14讲:手拉手模型常见结论的证明和应用 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 17:23:52 | ||
图片预览




文档简介
(共11张PPT)
《“手拉手”模型常用结论的证明及应用》
模块一 全等“手拉手”
深圳市桂园中学 苏剑平
全等“手拉手”模型介绍
A
B
C
D
E
A
B
C
D
E
A
B
C
左手
右手
D
E
●
●
●
左手
左手
左手
右手
右手
右手
右手
右手
左手
左手
等边三角形
等腰直角三角形
一般等腰三角形
条件:共顶点、等顶角、双等腰.
模块一:全等“手拉手”
例1:如图,在线段BD上取一点A,在同侧作等边△ABC和等边△ADE,连接BE、CD,
求证:(1)△ABE≌△ACD; (2)BE=CD; (3)△AFB≌△AGC; (4)△AFE≌△AGD;
(5)△AFG是等边三角形;(6)∠COB=∠CAB; (7)OA平分∠BOD;(8)FG//BD.
A
E
D
C
B
O
G
F
模块一:全等“手拉手”
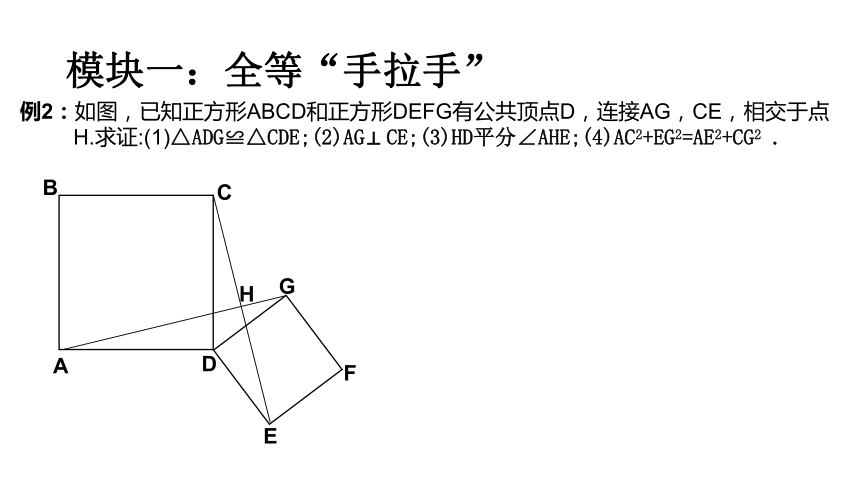
例2:如图,已知正方形ABCD和正方形DEFG有公共顶点D,连接AG,CE,相交于点
H.求证:(1)△ADG≌△CDE;(2)AG CE;(3)HD平分∠AHE;(4)AC2+EG2=AE2+CG2 .
A
B
C
D
E
F
G
H
《“手拉手”模型常用结论的证明及应用》
模块二 相似“手拉手”
深圳市桂园中学 苏剑平
相似“手拉手”模型介绍
条件:共顶点、等顶角、成比例.
A
D
C
B
E
A
B
C
D
E
DE//BC
模块二:相似“手拉手”
例3:如图,已知△ABC∽△ADE,求证:(1)△ABD∽△ACE; (2)∠BFC=∠BAC.
A
B
C
D
E
F
模块二:相似“手拉手”
例4:(2022秋 碑林区校级期中)如图,Rt△ABC与Rt△EDC,直角顶点重合于点C,点D在AB上,∠BAC=∠DEC且sin∠BAC= ,连接AE,若BD=2,AD=7,则AE长为( )
A. B. C. D.
《“手拉手”模型常用结论的证明及应用》
模块三 “手拉手”综合题
深圳市桂园中学 苏剑平
模块三:“手拉手”综合题
例5:(2019 玄武区一模)如图,四边形ABCD和四边形AEFG均为正方形,连接CF,DG,则 =( )
A. B. C. D.
模块三:“手拉手”综合题
例6:(2022 深圳中考)已知△ABC是直角三角形,∠ABC=90°,AB=3,BC=5,AE=2 ,连接CE,以CE为底作直角三角形CDE,且CD=DE.F是AE边上的一点,连接BD和BF,且∠FBD=45°,则AF长为__________.
《“手拉手”模型常用结论的证明及应用》
模块一 全等“手拉手”
深圳市桂园中学 苏剑平
全等“手拉手”模型介绍
A
B
C
D
E
A
B
C
D
E
A
B
C
左手
右手
D
E
●
●
●
左手
左手
左手
右手
右手
右手
右手
右手
左手
左手
等边三角形
等腰直角三角形
一般等腰三角形
条件:共顶点、等顶角、双等腰.
模块一:全等“手拉手”
例1:如图,在线段BD上取一点A,在同侧作等边△ABC和等边△ADE,连接BE、CD,
求证:(1)△ABE≌△ACD; (2)BE=CD; (3)△AFB≌△AGC; (4)△AFE≌△AGD;
(5)△AFG是等边三角形;(6)∠COB=∠CAB; (7)OA平分∠BOD;(8)FG//BD.
A
E
D
C
B
O
G
F
模块一:全等“手拉手”
例2:如图,已知正方形ABCD和正方形DEFG有公共顶点D,连接AG,CE,相交于点
H.求证:(1)△ADG≌△CDE;(2)AG CE;(3)HD平分∠AHE;(4)AC2+EG2=AE2+CG2 .
A
B
C
D
E
F
G
H
《“手拉手”模型常用结论的证明及应用》
模块二 相似“手拉手”
深圳市桂园中学 苏剑平
相似“手拉手”模型介绍
条件:共顶点、等顶角、成比例.
A
D
C
B
E
A
B
C
D
E
DE//BC
模块二:相似“手拉手”
例3:如图,已知△ABC∽△ADE,求证:(1)△ABD∽△ACE; (2)∠BFC=∠BAC.
A
B
C
D
E
F
模块二:相似“手拉手”
例4:(2022秋 碑林区校级期中)如图,Rt△ABC与Rt△EDC,直角顶点重合于点C,点D在AB上,∠BAC=∠DEC且sin∠BAC= ,连接AE,若BD=2,AD=7,则AE长为( )
A. B. C. D.
《“手拉手”模型常用结论的证明及应用》
模块三 “手拉手”综合题
深圳市桂园中学 苏剑平
模块三:“手拉手”综合题
例5:(2019 玄武区一模)如图,四边形ABCD和四边形AEFG均为正方形,连接CF,DG,则 =( )
A. B. C. D.
模块三:“手拉手”综合题
例6:(2022 深圳中考)已知△ABC是直角三角形,∠ABC=90°,AB=3,BC=5,AE=2 ,连接CE,以CE为底作直角三角形CDE,且CD=DE.F是AE边上的一点,连接BD和BF,且∠FBD=45°,则AF长为__________.
同课章节目录
