深圳市中考备考百师助学培优课程——第10讲:求线段比问题 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第10讲:求线段比问题 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 335.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 17:23:52 | ||
图片预览




文档简介
(共14张PPT)
求线段比问题的常见解决方法
布心中学刘蕊
罗湖区中考备考“百师助学”课程
模块一:作平行线构造相似三角形
利用相似三角形对应边成比例
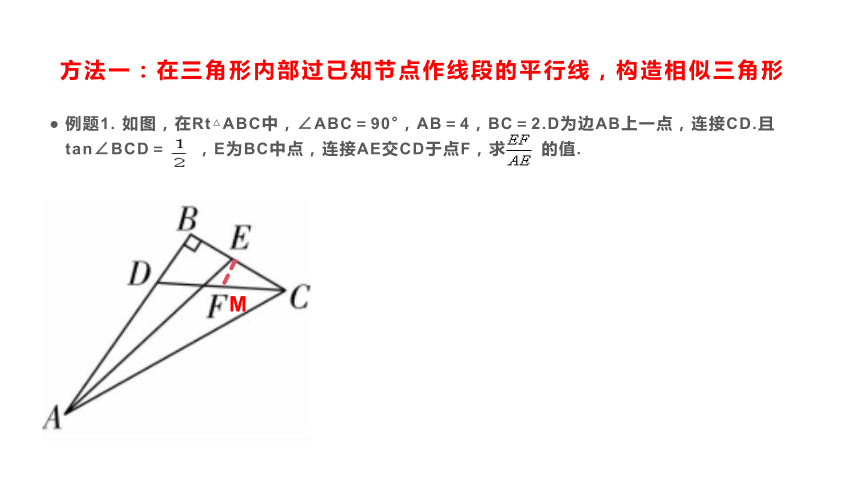
方法一:在三角形内部过已知节点作线段的平行线,构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
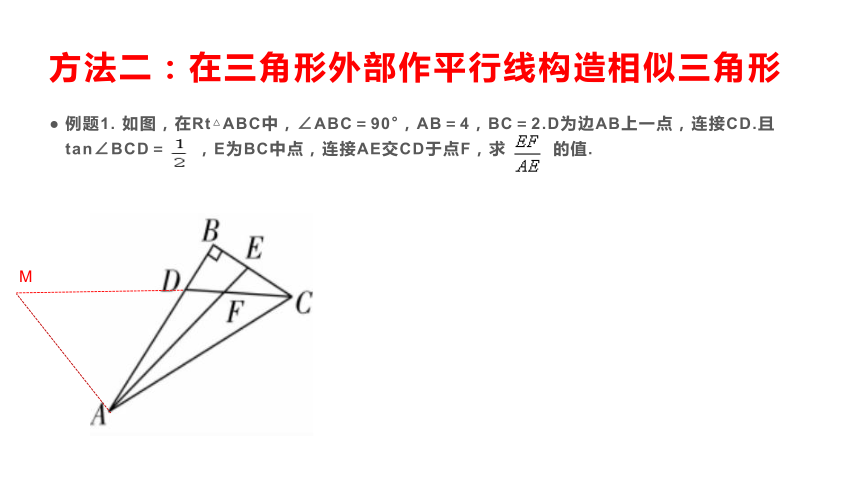
方法二:在三角形外部作平行线构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
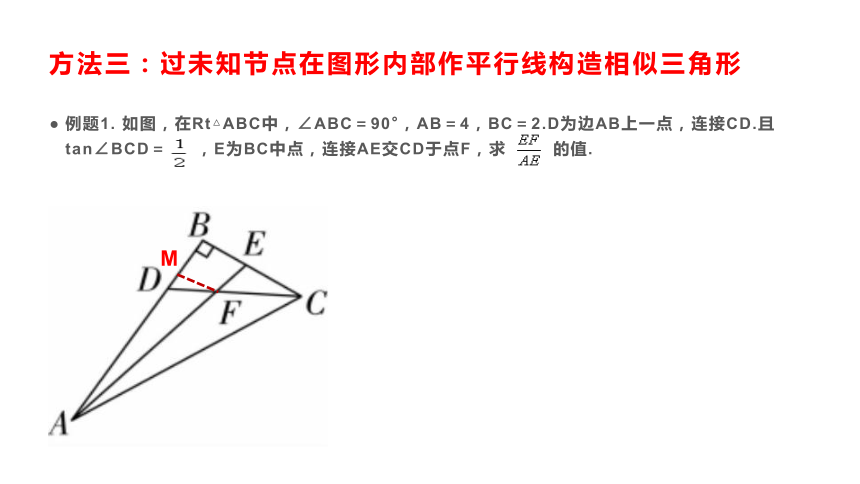
方法三:过未知节点在图形内部作平行线构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
感 谢 聆 听!
模块二:通过作垂直线段求线段比
方法一:遇30度,45度,60度等特殊角作垂直
例.如图,在 ABCD中,AD=BD,∠ADC=105°,点E在AD上,∠EBA=60°,则 的值是( )
M
N
方法二:遇等腰三角形,利用三线合一作垂直
例.如图,在 ABCD中,AD=BD,∠ADC=105°,点E在AD上,∠EBA=60°,则 的值是( )
M
N
感 谢 聆 听!
模块三:图形变换中求线段比
方法一:折叠图形中的线段比---找相等角,相等线段
例.如图,在△ABC中,AB=AC,tanB= ,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则
= .
M
N
方法二:折叠图形中,对应角相等,三角函数值也相等
例.如图,在△ABC中,AB=AC,tanB= ,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则
= .
M
感 谢 聆 听!
求线段比问题的常见解决方法
布心中学刘蕊
罗湖区中考备考“百师助学”课程
模块一:作平行线构造相似三角形
利用相似三角形对应边成比例
方法一:在三角形内部过已知节点作线段的平行线,构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
方法二:在三角形外部作平行线构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
方法三:过未知节点在图形内部作平行线构造相似三角形
例题1. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.D为边AB上一点,连接CD.且tan∠BCD= ,E为BC中点,连接AE交CD于点F,求 的值.
M
感 谢 聆 听!
模块二:通过作垂直线段求线段比
方法一:遇30度,45度,60度等特殊角作垂直
例.如图,在 ABCD中,AD=BD,∠ADC=105°,点E在AD上,∠EBA=60°,则 的值是( )
M
N
方法二:遇等腰三角形,利用三线合一作垂直
例.如图,在 ABCD中,AD=BD,∠ADC=105°,点E在AD上,∠EBA=60°,则 的值是( )
M
N
感 谢 聆 听!
模块三:图形变换中求线段比
方法一:折叠图形中的线段比---找相等角,相等线段
例.如图,在△ABC中,AB=AC,tanB= ,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则
= .
M
N
方法二:折叠图形中,对应角相等,三角函数值也相等
例.如图,在△ABC中,AB=AC,tanB= ,点D为BC上一动点,连接AD,将△ABD沿AD翻折得到△ADE,DE交AC于点G,GE<DG,且AG:CG=3:1,则
= .
M
感 谢 聆 听!
同课章节目录
