深圳市中考备考百师助学培优课程——第6讲:折叠问题 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第6讲:折叠问题 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 17:23:52 | ||
图片预览




文档简介
第一讲:折叠问题 自主学习单
一、知识技能梳理
模块一:折叠与全等
折叠,是几何学中一个基本而有趣的操作。通过折叠,我们可以将一个二维的图形转化为三维的立体形状,或者将一个复杂的图形简化为一个更易于理解和分析的形式。折叠的规则和原理,如轴对称、中心对称等,都是几何学中的重要内容。理解并应用这些规则,可以帮助我们更好地理解和解决几何问题。
全等,则是另一个重要的数学概念。当两个图形在形状和大小上都完全相同时,我们就说这两个图形是全等的。全等图形的性质和判定方法,如SSS、SAS、ASA、AAS等,都是我们在学习和应用数学时需要掌握的基本知识。
折叠与全等,有着紧密的联系。通过折叠,我们可以得到全等的图形;同时,全等图形的性质也可以在折叠中得到验证和应用。在学习和理解这两个概念的过程中,我们可以培养自己的逻辑思维和空间想象能力,为未来的数学学习和实际应用打下坚实的基础。
模块二:折叠与相似
相似的图形,虽然大小不同,但形状却完全相同。这种相似性使得我们能够在不同的尺度上研究同一类图形,从而发现它们之间的共同规律。在建筑设计中,相似原理被广泛应用。建筑师们通过调整建筑的比例和尺寸,创造出既美观又实用的建筑作品。这些作品不仅体现了数学的美,更展示了人类文明的智慧。
折叠与相似,虽然看似不同,但在实际应用中却常常相互关联。在图形变换中,我们可以通过折叠得到相似的图形;而在相似图形中,我们也可以找到折叠的规律。这种相互依存的关系,使得折叠与相似成为了数学中不可或缺的一部分。
模块三:折叠与动点
动点是指在几何图形中可以移动的点,具有位置的变化性和不确定性。在几何学中,动点常用于研究图形的运动和变换。
模块四:折叠与函数
折叠与函数的关系:在数学中,函数是一种特殊的对应关系,它描述了自变量与因变量之间的关系。折叠与函数之间存在着密切的关系。我们可以通过折叠来探究函数的性质,也可以通过函数来描述折叠的规律。例如,当我们将一个图形沿x轴折叠时,对应的y值会发生变化,这种变化可以用函数来描述。通过折叠与函数的结合,我们可以更深入地理解函数的性质和应用。
为了更好地理解折叠与函数的关系,我们可以通过一些实例来进行探究。例如,我们可以考虑一个二次函数y = ax^2 + bx + c的图像,并将其沿x轴折叠。通过观察折叠后的图像,我们可以发现折叠后的图像关于x轴对称,这与二次函数的性质是一致的。此外,我们还可以通过折叠来探究函数的周期性、奇偶性等性质,从而加深对函数的理解。
二、基本模型展示
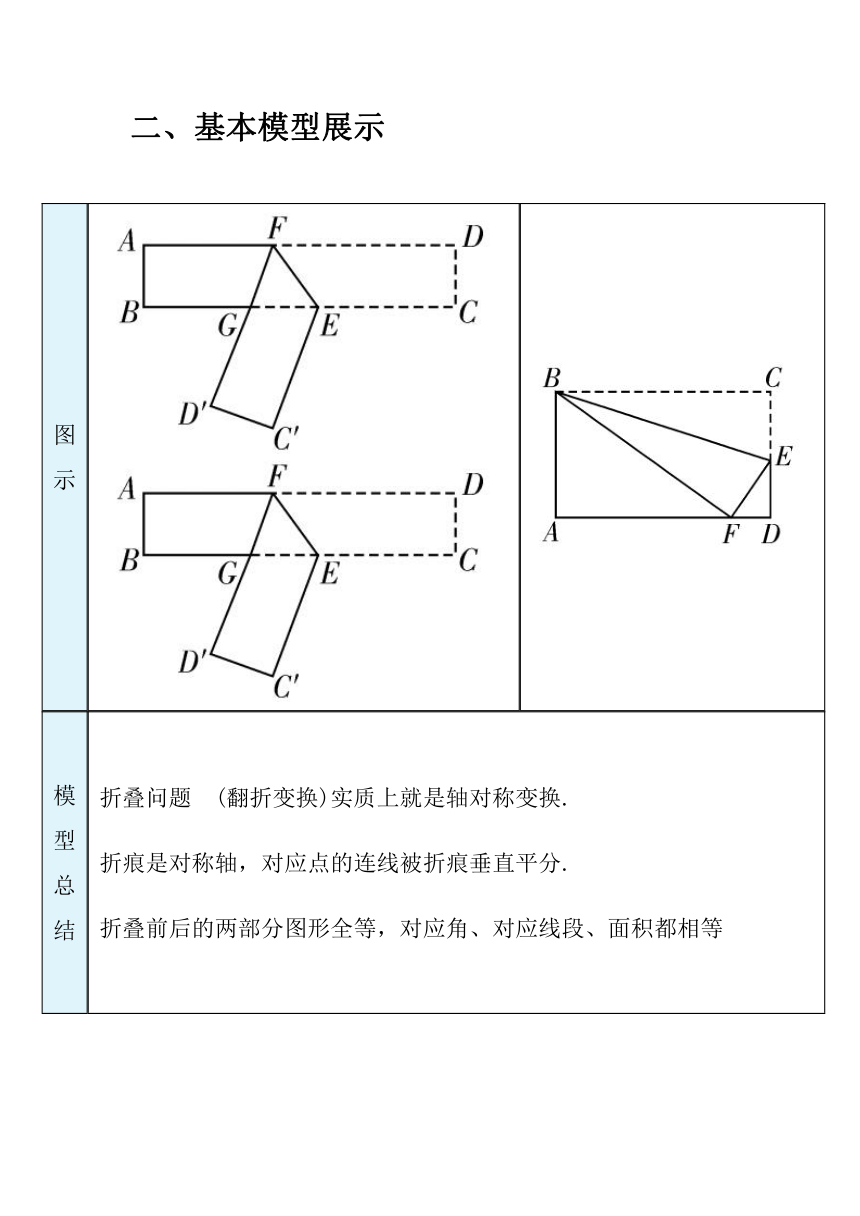
图示
模型总结 折叠问题 (翻折变换)实质上就是轴对称变换. 折痕是对称轴,对应点的连线被折痕垂直平分. 折叠前后的两部分图形全等,对应角、对应线段、面积都相等
学习过程
模块一:折叠与全等
1.针对训练
例1.(教材改编)如图W-4-1,在□ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在点B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
求证:(1)∠1=∠2;
(2)DG=B′G.
证明:(1)在□ABCD中,DC∥AB,∴∠2=∠FEC.
由折叠的性质,得∠1=∠FEC,∴∠1=∠2.
(2)∵∠1=∠2,∴EG=GF.
∵AB∥DC,∴∠DEG=∠EGF.
由折叠的性质,得EC′∥B′F,
∴∠B′FG=∠EGF.∴∠DEG=∠B′FG.
又∵DE=BF=B′F,∴△DEG≌△B′FG(SAS).
∴DG=B′G.
针对巩固
2.(教材改编)如图W-4-2,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E .
(1)找出一个与△AED全等的三
角形,并加以证明;
(2)已知AD=4,CD=8,求
△AEC的面积.
模块二:折叠与相似
针对训练
解:(1)相似的三角形有:△ADE∽△AFE,△ABF∽△FCE.
证明如下:∵将△ADE沿AE折叠,点D恰好落在边BC上的点F处,∴△ADE≌△AFE.∴△ADE∽△AFE.∴∠AFE=∠D=90°.∴∠AFB+∠BAF=∠AFB+∠CFE=90°.∴∠BAF=∠CFE.
又∵∠B=∠C=90°,∴△ABF∽△FCE.
2.针对巩固
练习2
模块三:折叠与动点
1.针对训练
2.针对巩固
3.(教材改编)如图W-4-6,在矩形ABCD中,AD=6,AB=10,点E在AB上,点F是AD上的动点,将矩形ABCD沿EF折叠,使点A落在边CD上的点G处,当点G在边CD上移动时,求折痕EF的最大值.
模块四:折叠与函数
1.针对训练
2.针对巩固
4.(教材改编)如图W-4-8,在平面直角坐标系中,点A,B的坐标分别是(0,8),(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在直线交y轴正半轴于点C.
(1)求直线BC的函数表达式;
(2)把直线BC向左平移,使之经过点
A′,求平移后直线的函数表达式.
练习
1.如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处,,,则的长为( )
A. B. C. D.
2.如图,正方形 ABCD的边长为 9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,折痕为GH.若 BE:EC=2:1,则线段 CH 的长为( )
A.3 B.4 C.5 D.6
3.如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A.BD=10 B.HG=2 C. D.GF⊥BC
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E,F.以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE.
A.①②③ B.②④ C.①③④ D.①②③④
5.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上.给出以下结论:
①△ADE≌△FCD;② ;
③ ;④当AE=1时,BE= ,
其中正确的结论共有( ).
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
7.如图1,点Q为菱形ABCD的边BC上一点,将菱形 ABCD沿直线AQ 翻折,点B的对应点P落在BC的延长线上.已知动点M从点B出发,在射线 BC上以每秒1个单位长度运动.设点M运动的时间为x,△APM的面积为y.图2为y关于x的函数图象,则菱形 ABCD的面积为( )
A.12 B.24 C.10 D.20
8.如图,在矩形中,,,是的中点,将沿直线翻折,点落在点处,连接,则的长为( )
A.8 B. C. D.
参考答案
1.如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处,,,则的长为( )
A. B. C. D.
【答案】A
【解析】【解答】解:∵ 四边形ABCD为矩形,
∴ AB=CD,AD=BC,
∵把沿翻折,使点恰好落在边上的点处,
∴ AF=AD=4,EF=DE=,
在Rt△ABF中,BF==2,
∴ CF=BC-BF=2,
在Rt△CEF中,
即
解得,EC= .
故答案为:A.
【分析】根据矩形的性质得 AB=CD,AD=BC,根据翻折的性质得 AF=AD=4,EF=DE=,根据勾股定理得BF从而推出CF,再根据勾股定理得EC,即可求得.
2.如图,正方形 ABCD的边长为 9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,折痕为GH.若 BE:EC=2:1,则线段 CH 的长为( )
A.3 B.4 C.5 D.6
【答案】B
【解析】【解答】解:∵BE:EC=2:1,BE+EC=9
∴EC=3;
∵正方形 ABCD的边长为9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,
∴∠C=90°,DH=EH,
设CH=x,则DH=EH=9-x,
在Rt△ECH中
CH2+CE2=EH2即x2+9=(9-x)2
解之:x=4,
∴CH的长为4.
故答案为:B.
【分析】利用已知求出EC的长,利用正方形的性质和折叠的性质可得到∠C=90°,DH=EH,设CH=x,则DH=EH=9-x,在Rt△ECH中利用勾股定理可得到关于x的方程,解方程求出x的值,可得到CH的长.
3.如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A.BD=10 B.HG=2 C. D.GF⊥BC
【答案】D
【解析】【解答】解:BD是矩形ABCD的对角线,AB=6,BC=8,
故A选项正确;
将△ABE沿BE翻折,将△DCF沿DF翻折,
,
,
故B选项正确;
,
∴EG∥HF,
故C正确;
设,则,
,
即
,同理可得
若
则
,
,
∴FG不平行CD,
即GF不垂直BC,
故D不正确.
故答案为:D.
【分析】由矩形的性质得BC=AD=8,AB=CD=6,用勾股定理算出BD=10,据此可判断A选项;由翻折的性质得BG=AB=6,DH=CD=6,根据线段的和差可得DG=BH=4,HG=2,据此可判断B选项;由翻折可得∠EGB=∠A=∠DHF=∠C=90°,由内错角相等,两直线平行,可得EG∥HF,据此判断C选项;设AE=a,则EG=a,ED=8-a,由∠ADB的正切函数的定义可得,据此可求出AE的长,同理可得CF的长,若FG∥CD,由平行线分线段成比例定理得,而根据线段的长度可得,故FG不平行CD,即GF不垂直BC,据此可判断D选项.
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E,F.以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE.
A.①②③ B.②④ C.①③④ D.①②③④
【答案】C
【解析】【解答】解:∵ 将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,
∴∠BAE=∠EAD=∠BAD,∠CAF=∠DAF=∠CAD,
∴∠EAF=∠EAD+∠DAF=(∠BAD+∠CAD)=∠BAC=×90°=45°,故①正确;
∵∠BAC=90°,∠C=30°,
∴∠B=60°=∠BDA=∠CDF,∠C'=30°,
∴△ABD是等边三角形,∠C'FD=90°,DF=m,则C'D=2m,C'F=CF=,
∴CD=DF+CF=,
∵∠BDA=60°,∠C=30°,
∴∠DAC=∠C=30°,
∴DC=AD==BD
∴BE=DE=BD=,而C'F=,
∴C'F≠BE,故②错误;
∵CD=,BE=DE=,
∴CE=CD+CD=,故③正确;
∵∠BEC=90°,∠C=30°,
∴,
∴,
∴FC= (-1)AE ,故④正确,
综上,正确的有①③④.
故答案为:C.
【分析】由翻折得∠BAE=∠EAD=∠BAD,∠CAF=∠DAF=∠CAD,进而根据∠EAF=∠EAD+∠DAF可判断①;由三角形的内角和定理及翻折得∠B=60°=∠BDA=∠CDF,∠C'=30°,则△ABD是等边三角形,∠C'FD=90°,DF=m,则C'D=2m,C'F=CF=,进而根据三角形外角性质得∠DAC=∠C=30°,由等边对等角及线段的和差得DC=AD==BD,则E=DE=BD=,可判断②;由CE=CD+CD算出CE的长,可判断③;由含30°角直角三角形的性质得,从而代入 (-1)AE 算出结果可判断④.
5.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上.给出以下结论:
①△ADE≌△FCD;② ;
③ ;④当AE=1时,BE= ,
其中正确的结论共有( ).
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】【解答】解:∵四边形ABCD为矩形
∴设EF=BE=x,则AB=CD=1+x
又∵AB∥CD
∴∠DCE=∠BEC
由折叠的性质可得,∠BEC=∠DEC
∴∠DCE=∠DEC
∴DE=CD=1+x
∴点E,F,D在同一条直线上
∴DF=DE-EF=1+x-x=1=AE
∵AB∥CD
∴△DCF∽△EAF
∴=
∴
解得,x1=,x2=(舍去)
∴BE=x=,即④正确;
由以上可得,DE=CD,DF=AE,∠AED=∠FDC
∴△ADE≌△FCD,即①正确;
由题意,S△ADE=AE×AD,S△ACE=AE×AD
∴S△ADE=S△ACE
由折叠的性质可得,S△BCE=S△FCE
∴S△ADE=S△AEF+S△BCE
∴S△ADF+S△AEF=S△AEF+S△BCE
∴S△ADF=S△BCE,即②正确;
∵tan∠ACE=tan∠BCE==,即③错误
故答案为:C.
【分析】根据矩形的性质、折叠的性质,结合三角形全等、相似的判定定理和性质,分别进行证明即可。
6.在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
【答案】A
【解析】【解答】过C作CD⊥AB于D,如图,
对于直线y=-x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3-n,
∴DA=OA=4,
∴DB=5-4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3-n)2,解得n=,
∴点C的坐标为(0,).
故选:A.
【分析】过C作CD⊥AB于D,先求出A,B的坐标,分别为(4,0),(0,3),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=4,则DB=5-4=1,BC=3-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.本题考查了求直线与坐标轴交点的坐标的方法:分别令x=0或y=0,求对应的y或x的值;也考查了折叠的性质和勾股定理.
7.如图1,点Q为菱形ABCD的边BC上一点,将菱形 ABCD沿直线AQ 翻折,点B的对应点P落在BC的延长线上.已知动点M从点B出发,在射线 BC上以每秒1个单位长度运动.设点M运动的时间为x,△APM的面积为y.图2为y关于x的函数图象,则菱形 ABCD的面积为( )
A.12 B.24 C.10 D.20
【答案】D
【解析】【解答】解:由图2,得BP=6,S△ABP=12
由翻折可知,AQ⊥BP
∴AQ=4
由勾股定理,得BC=AB==5
∴菱形ABCD的面积为BC×AQ=5×4=20
故答案为:D.
【分析】由翻折可知AQ⊥BP,由图2信息可得BP=2BQ=6,S△ABP=12,根据S△ABP=BP·AQ=12,可求出AQ=4,利用勾股定理求出BC=AB=5,根据菱形 ABCD的面积为BC×AQ即可求解.
8.如图,在矩形中,,,是的中点,将沿直线翻折,点落在点处,连接,则的长为( )
A.8 B. C. D.
【答案】B
【解析】【解答】解:过点E作EG⊥CF于点G,
∵四边形ABCD为矩形,
∴∠B=90°.
∵AB=2,BC=,点E是BC的中点,
∴BE=CE=,
∴AE==5.
由折叠可得∠AEB=∠AEF=∠BEF,BE=EF,
∴CE=EF.
∵EG⊥CF,
∴∠CEG=∠FEG=∠CEF,CG=FG,
∴∠AEB+∠CEG=∠BEF+∠CEF=(∠BEF+∠CEF)=90°.
∵∠ECG+∠CEG=90°,
∴∠AEB=∠ECG.
∵∠B=∠CGE=90°,
∴△ABE∽△EGC,
∴,
∴,
∴CG=,
∴CF=2CG=.
故答案为:B.
【分析】过点E作EG⊥CF于点G,根据矩形的性质可得∠B=90°,由中点的概念可得BE=CE=,利用勾股定理可得AE的值,由折叠可得∠AEB=∠AEF=∠BEF,BE=EF,则CE=EF,结合等腰三角形的性质可得∠CEG=∠FEG=∠CEF,CG=FG,则∠AEB+∠CEG=(∠BEF+∠CEF)=90°,利用两角对应相等的两个三角形相似可得△ABE∽△EGC,根据相似三角形的性质可得CG,进而可得CF.
一、知识技能梳理
模块一:折叠与全等
折叠,是几何学中一个基本而有趣的操作。通过折叠,我们可以将一个二维的图形转化为三维的立体形状,或者将一个复杂的图形简化为一个更易于理解和分析的形式。折叠的规则和原理,如轴对称、中心对称等,都是几何学中的重要内容。理解并应用这些规则,可以帮助我们更好地理解和解决几何问题。
全等,则是另一个重要的数学概念。当两个图形在形状和大小上都完全相同时,我们就说这两个图形是全等的。全等图形的性质和判定方法,如SSS、SAS、ASA、AAS等,都是我们在学习和应用数学时需要掌握的基本知识。
折叠与全等,有着紧密的联系。通过折叠,我们可以得到全等的图形;同时,全等图形的性质也可以在折叠中得到验证和应用。在学习和理解这两个概念的过程中,我们可以培养自己的逻辑思维和空间想象能力,为未来的数学学习和实际应用打下坚实的基础。
模块二:折叠与相似
相似的图形,虽然大小不同,但形状却完全相同。这种相似性使得我们能够在不同的尺度上研究同一类图形,从而发现它们之间的共同规律。在建筑设计中,相似原理被广泛应用。建筑师们通过调整建筑的比例和尺寸,创造出既美观又实用的建筑作品。这些作品不仅体现了数学的美,更展示了人类文明的智慧。
折叠与相似,虽然看似不同,但在实际应用中却常常相互关联。在图形变换中,我们可以通过折叠得到相似的图形;而在相似图形中,我们也可以找到折叠的规律。这种相互依存的关系,使得折叠与相似成为了数学中不可或缺的一部分。
模块三:折叠与动点
动点是指在几何图形中可以移动的点,具有位置的变化性和不确定性。在几何学中,动点常用于研究图形的运动和变换。
模块四:折叠与函数
折叠与函数的关系:在数学中,函数是一种特殊的对应关系,它描述了自变量与因变量之间的关系。折叠与函数之间存在着密切的关系。我们可以通过折叠来探究函数的性质,也可以通过函数来描述折叠的规律。例如,当我们将一个图形沿x轴折叠时,对应的y值会发生变化,这种变化可以用函数来描述。通过折叠与函数的结合,我们可以更深入地理解函数的性质和应用。
为了更好地理解折叠与函数的关系,我们可以通过一些实例来进行探究。例如,我们可以考虑一个二次函数y = ax^2 + bx + c的图像,并将其沿x轴折叠。通过观察折叠后的图像,我们可以发现折叠后的图像关于x轴对称,这与二次函数的性质是一致的。此外,我们还可以通过折叠来探究函数的周期性、奇偶性等性质,从而加深对函数的理解。
二、基本模型展示
图示
模型总结 折叠问题 (翻折变换)实质上就是轴对称变换. 折痕是对称轴,对应点的连线被折痕垂直平分. 折叠前后的两部分图形全等,对应角、对应线段、面积都相等
学习过程
模块一:折叠与全等
1.针对训练
例1.(教材改编)如图W-4-1,在□ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在点B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
求证:(1)∠1=∠2;
(2)DG=B′G.
证明:(1)在□ABCD中,DC∥AB,∴∠2=∠FEC.
由折叠的性质,得∠1=∠FEC,∴∠1=∠2.
(2)∵∠1=∠2,∴EG=GF.
∵AB∥DC,∴∠DEG=∠EGF.
由折叠的性质,得EC′∥B′F,
∴∠B′FG=∠EGF.∴∠DEG=∠B′FG.
又∵DE=BF=B′F,∴△DEG≌△B′FG(SAS).
∴DG=B′G.
针对巩固
2.(教材改编)如图W-4-2,将矩形纸片ABCD沿对角线AC折叠,使点B落到点F的位置,AF与CD交于点E .
(1)找出一个与△AED全等的三
角形,并加以证明;
(2)已知AD=4,CD=8,求
△AEC的面积.
模块二:折叠与相似
针对训练
解:(1)相似的三角形有:△ADE∽△AFE,△ABF∽△FCE.
证明如下:∵将△ADE沿AE折叠,点D恰好落在边BC上的点F处,∴△ADE≌△AFE.∴△ADE∽△AFE.∴∠AFE=∠D=90°.∴∠AFB+∠BAF=∠AFB+∠CFE=90°.∴∠BAF=∠CFE.
又∵∠B=∠C=90°,∴△ABF∽△FCE.
2.针对巩固
练习2
模块三:折叠与动点
1.针对训练
2.针对巩固
3.(教材改编)如图W-4-6,在矩形ABCD中,AD=6,AB=10,点E在AB上,点F是AD上的动点,将矩形ABCD沿EF折叠,使点A落在边CD上的点G处,当点G在边CD上移动时,求折痕EF的最大值.
模块四:折叠与函数
1.针对训练
2.针对巩固
4.(教材改编)如图W-4-8,在平面直角坐标系中,点A,B的坐标分别是(0,8),(6,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在直线交y轴正半轴于点C.
(1)求直线BC的函数表达式;
(2)把直线BC向左平移,使之经过点
A′,求平移后直线的函数表达式.
练习
1.如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处,,,则的长为( )
A. B. C. D.
2.如图,正方形 ABCD的边长为 9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,折痕为GH.若 BE:EC=2:1,则线段 CH 的长为( )
A.3 B.4 C.5 D.6
3.如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A.BD=10 B.HG=2 C. D.GF⊥BC
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E,F.以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE.
A.①②③ B.②④ C.①③④ D.①②③④
5.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上.给出以下结论:
①△ADE≌△FCD;② ;
③ ;④当AE=1时,BE= ,
其中正确的结论共有( ).
A.1个 B.2个 C.3个 D.4个
6.在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
7.如图1,点Q为菱形ABCD的边BC上一点,将菱形 ABCD沿直线AQ 翻折,点B的对应点P落在BC的延长线上.已知动点M从点B出发,在射线 BC上以每秒1个单位长度运动.设点M运动的时间为x,△APM的面积为y.图2为y关于x的函数图象,则菱形 ABCD的面积为( )
A.12 B.24 C.10 D.20
8.如图,在矩形中,,,是的中点,将沿直线翻折,点落在点处,连接,则的长为( )
A.8 B. C. D.
参考答案
1.如图,在矩形中,为边上一点,把沿翻折,使点恰好落在边上的点处,,,则的长为( )
A. B. C. D.
【答案】A
【解析】【解答】解:∵ 四边形ABCD为矩形,
∴ AB=CD,AD=BC,
∵把沿翻折,使点恰好落在边上的点处,
∴ AF=AD=4,EF=DE=,
在Rt△ABF中,BF==2,
∴ CF=BC-BF=2,
在Rt△CEF中,
即
解得,EC= .
故答案为:A.
【分析】根据矩形的性质得 AB=CD,AD=BC,根据翻折的性质得 AF=AD=4,EF=DE=,根据勾股定理得BF从而推出CF,再根据勾股定理得EC,即可求得.
2.如图,正方形 ABCD的边长为 9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,折痕为GH.若 BE:EC=2:1,则线段 CH 的长为( )
A.3 B.4 C.5 D.6
【答案】B
【解析】【解答】解:∵BE:EC=2:1,BE+EC=9
∴EC=3;
∵正方形 ABCD的边长为9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,
∴∠C=90°,DH=EH,
设CH=x,则DH=EH=9-x,
在Rt△ECH中
CH2+CE2=EH2即x2+9=(9-x)2
解之:x=4,
∴CH的长为4.
故答案为:B.
【分析】利用已知求出EC的长,利用正方形的性质和折叠的性质可得到∠C=90°,DH=EH,设CH=x,则DH=EH=9-x,在Rt△ECH中利用勾股定理可得到关于x的方程,解方程求出x的值,可得到CH的长.
3.如图,已知BD是矩形ABCD的对角线,AB=6,BC=8,点E,F分别在边AD,BC上,连结BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在对角线BD上的点G,H处,连结GF.则下列结论不正确的是( )
A.BD=10 B.HG=2 C. D.GF⊥BC
【答案】D
【解析】【解答】解:BD是矩形ABCD的对角线,AB=6,BC=8,
故A选项正确;
将△ABE沿BE翻折,将△DCF沿DF翻折,
,
,
故B选项正确;
,
∴EG∥HF,
故C正确;
设,则,
,
即
,同理可得
若
则
,
,
∴FG不平行CD,
即GF不垂直BC,
故D不正确.
故答案为:D.
【分析】由矩形的性质得BC=AD=8,AB=CD=6,用勾股定理算出BD=10,据此可判断A选项;由翻折的性质得BG=AB=6,DH=CD=6,根据线段的和差可得DG=BH=4,HG=2,据此可判断B选项;由翻折可得∠EGB=∠A=∠DHF=∠C=90°,由内错角相等,两直线平行,可得EG∥HF,据此判断C选项;设AE=a,则EG=a,ED=8-a,由∠ADB的正切函数的定义可得,据此可求出AE的长,同理可得CF的长,若FG∥CD,由平行线分线段成比例定理得,而根据线段的长度可得,故FG不平行CD,即GF不垂直BC,据此可判断D选项.
4.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,两条折痕与斜边BC分别交于E,F.以下四个结论正确的是( )
①∠EAF=45°;②FC′=BE;③EC=3BE;④FC=(-1)AE.
A.①②③ B.②④ C.①③④ D.①②③④
【答案】C
【解析】【解答】解:∵ 将边AB沿着AE翻折,使点B落在BC上的点D处,再将边AC沿着AF翻折,使得C落在AD延长线上的点C′处,
∴∠BAE=∠EAD=∠BAD,∠CAF=∠DAF=∠CAD,
∴∠EAF=∠EAD+∠DAF=(∠BAD+∠CAD)=∠BAC=×90°=45°,故①正确;
∵∠BAC=90°,∠C=30°,
∴∠B=60°=∠BDA=∠CDF,∠C'=30°,
∴△ABD是等边三角形,∠C'FD=90°,DF=m,则C'D=2m,C'F=CF=,
∴CD=DF+CF=,
∵∠BDA=60°,∠C=30°,
∴∠DAC=∠C=30°,
∴DC=AD==BD
∴BE=DE=BD=,而C'F=,
∴C'F≠BE,故②错误;
∵CD=,BE=DE=,
∴CE=CD+CD=,故③正确;
∵∠BEC=90°,∠C=30°,
∴,
∴,
∴FC= (-1)AE ,故④正确,
综上,正确的有①③④.
故答案为:C.
【分析】由翻折得∠BAE=∠EAD=∠BAD,∠CAF=∠DAF=∠CAD,进而根据∠EAF=∠EAD+∠DAF可判断①;由三角形的内角和定理及翻折得∠B=60°=∠BDA=∠CDF,∠C'=30°,则△ABD是等边三角形,∠C'FD=90°,DF=m,则C'D=2m,C'F=CF=,进而根据三角形外角性质得∠DAC=∠C=30°,由等边对等角及线段的和差得DC=AD==BD,则E=DE=BD=,可判断②;由CE=CD+CD算出CE的长,可判断③;由含30°角直角三角形的性质得,从而代入 (-1)AE 算出结果可判断④.
5.如图是一张矩形纸片,点E在AB边上,把△BCE沿直线CE对折,使点B在对角线AC上的点F处,连接DF.若点E,F,D在同一条直线上.给出以下结论:
①△ADE≌△FCD;② ;
③ ;④当AE=1时,BE= ,
其中正确的结论共有( ).
A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】【解答】解:∵四边形ABCD为矩形
∴设EF=BE=x,则AB=CD=1+x
又∵AB∥CD
∴∠DCE=∠BEC
由折叠的性质可得,∠BEC=∠DEC
∴∠DCE=∠DEC
∴DE=CD=1+x
∴点E,F,D在同一条直线上
∴DF=DE-EF=1+x-x=1=AE
∵AB∥CD
∴△DCF∽△EAF
∴=
∴
解得,x1=,x2=(舍去)
∴BE=x=,即④正确;
由以上可得,DE=CD,DF=AE,∠AED=∠FDC
∴△ADE≌△FCD,即①正确;
由题意,S△ADE=AE×AD,S△ACE=AE×AD
∴S△ADE=S△ACE
由折叠的性质可得,S△BCE=S△FCE
∴S△ADE=S△AEF+S△BCE
∴S△ADF+S△AEF=S△AEF+S△BCE
∴S△ADF=S△BCE,即②正确;
∵tan∠ACE=tan∠BCE==,即③错误
故答案为:C.
【分析】根据矩形的性质、折叠的性质,结合三角形全等、相似的判定定理和性质,分别进行证明即可。
6.在平面直角坐标系中,已知直线y=-x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
【答案】A
【解析】【解答】过C作CD⊥AB于D,如图,
对于直线y=-x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3-n,
∴DA=OA=4,
∴DB=5-4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3-n)2,解得n=,
∴点C的坐标为(0,).
故选:A.
【分析】过C作CD⊥AB于D,先求出A,B的坐标,分别为(4,0),(0,3),得到AB的长,再根据折叠的性质得到AC平分∠OAB,得到CD=CO=n,DA=OA=4,则DB=5-4=1,BC=3-n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.本题考查了求直线与坐标轴交点的坐标的方法:分别令x=0或y=0,求对应的y或x的值;也考查了折叠的性质和勾股定理.
7.如图1,点Q为菱形ABCD的边BC上一点,将菱形 ABCD沿直线AQ 翻折,点B的对应点P落在BC的延长线上.已知动点M从点B出发,在射线 BC上以每秒1个单位长度运动.设点M运动的时间为x,△APM的面积为y.图2为y关于x的函数图象,则菱形 ABCD的面积为( )
A.12 B.24 C.10 D.20
【答案】D
【解析】【解答】解:由图2,得BP=6,S△ABP=12
由翻折可知,AQ⊥BP
∴AQ=4
由勾股定理,得BC=AB==5
∴菱形ABCD的面积为BC×AQ=5×4=20
故答案为:D.
【分析】由翻折可知AQ⊥BP,由图2信息可得BP=2BQ=6,S△ABP=12,根据S△ABP=BP·AQ=12,可求出AQ=4,利用勾股定理求出BC=AB=5,根据菱形 ABCD的面积为BC×AQ即可求解.
8.如图,在矩形中,,,是的中点,将沿直线翻折,点落在点处,连接,则的长为( )
A.8 B. C. D.
【答案】B
【解析】【解答】解:过点E作EG⊥CF于点G,
∵四边形ABCD为矩形,
∴∠B=90°.
∵AB=2,BC=,点E是BC的中点,
∴BE=CE=,
∴AE==5.
由折叠可得∠AEB=∠AEF=∠BEF,BE=EF,
∴CE=EF.
∵EG⊥CF,
∴∠CEG=∠FEG=∠CEF,CG=FG,
∴∠AEB+∠CEG=∠BEF+∠CEF=(∠BEF+∠CEF)=90°.
∵∠ECG+∠CEG=90°,
∴∠AEB=∠ECG.
∵∠B=∠CGE=90°,
∴△ABE∽△EGC,
∴,
∴,
∴CG=,
∴CF=2CG=.
故答案为:B.
【分析】过点E作EG⊥CF于点G,根据矩形的性质可得∠B=90°,由中点的概念可得BE=CE=,利用勾股定理可得AE的值,由折叠可得∠AEB=∠AEF=∠BEF,BE=EF,则CE=EF,结合等腰三角形的性质可得∠CEG=∠FEG=∠CEF,CG=FG,则∠AEB+∠CEG=(∠BEF+∠CEF)=90°,利用两角对应相等的两个三角形相似可得△ABE∽△EGC,根据相似三角形的性质可得CG,进而可得CF.
同课章节目录
