深圳市中考备考百师助学培优课程——第8讲:用平行线解函数中三角形面积问题 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第8讲:用平行线解函数中三角形面积问题 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览



文档简介
罗湖区中考备考“百师助学”课程第八讲
《用平行线解函数中的三角形面积问题》
考点梳理:
函数与三角形面积相结合的综合题常常出现在中考的压轴题中,是中考压轴题的难点之一。主要考查学生的综合分析问题能力,考察学生数形结合思想,分类讨论思想、转化思想等。热点考题是:面积比问题,面积定值问题、面积最值问题,面积之间的和、差、比值等问题。常见的解题方法有多种,例如: 1、利用铅垂高、水平宽解决问题;2、利用割补法解决问题;3、利用面积比等于相似比的平方解决问题; 4、 利用平行线转移面积解决问题等。在二次函数与一次函数相结合的题目中求面积或者与面积相关的问题时,我们通常过三角形的某个已知顶点作对边的平行线,利用平滑定理来求解,问题就会变得简单许多,近年来,多地的中考试题中也出现了这样的题目,值得我们重视。
二、本节课学习目标:
1. 利用平行线转移三角形面积,并解决问题;
2. 利用平行线把面积比转化为线段比;
3. 通过直线与曲线相切求面积的最值;
三、新课学习:
知识铺垫:
知识铺垫:任何两条夹在平行线间的垂线段长度相等;
(1)如图1,若直线a∥b,则有MN=PQ
(2)如图2,直线a∥b,则S△ABC= S△BCD
我们先来了解什么是平滑定理:两个三角形共用同一底,且顶点都在与底平行的同一条直线上,那么由三角形的面积公式可知,这两个三角形的面积必然相等。所以平滑定理需要两个条件:(1)共底或者底在同一直线上但相等;(2)三角形的顶点都在与底平行的同一条直线上
知识铺垫2:一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行则可以推出k1=k2反之若k1=k2则可推出一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行,其中b1≠b2.
模块一(利用平行转换面积)
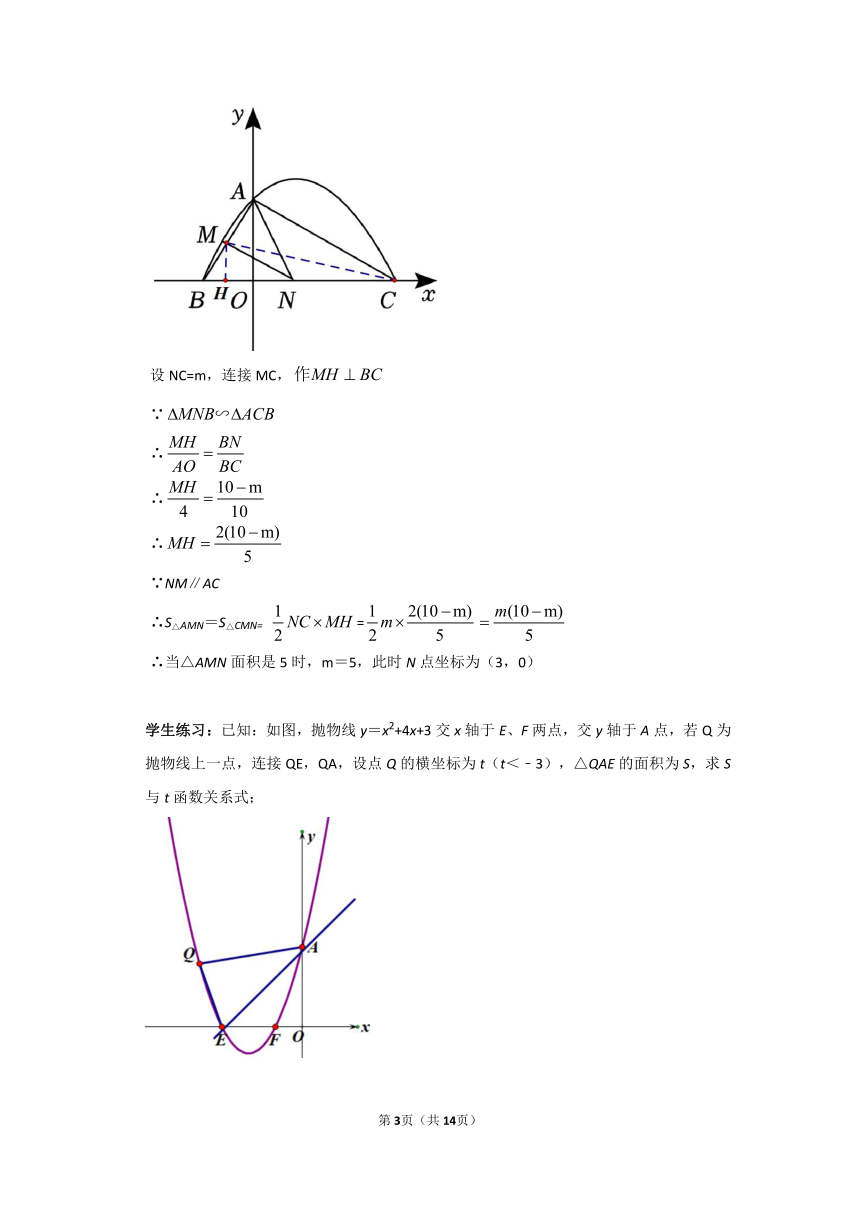
典例精讲: 如图,已知二次函数y=﹣x2+x+4的图象与y轴交于点A(0,4).与x轴交于点B,C,点C坐标为(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
解法1:A(0,4),B(-2,0), C(8,0)
设NC=m,连接MC,
∵
∴
∴
∴
∵NM∥AC
∴S△AMN=S△CMN= =
∴当△AMN面积是5时,m=5,此时N点坐标为(3,0)
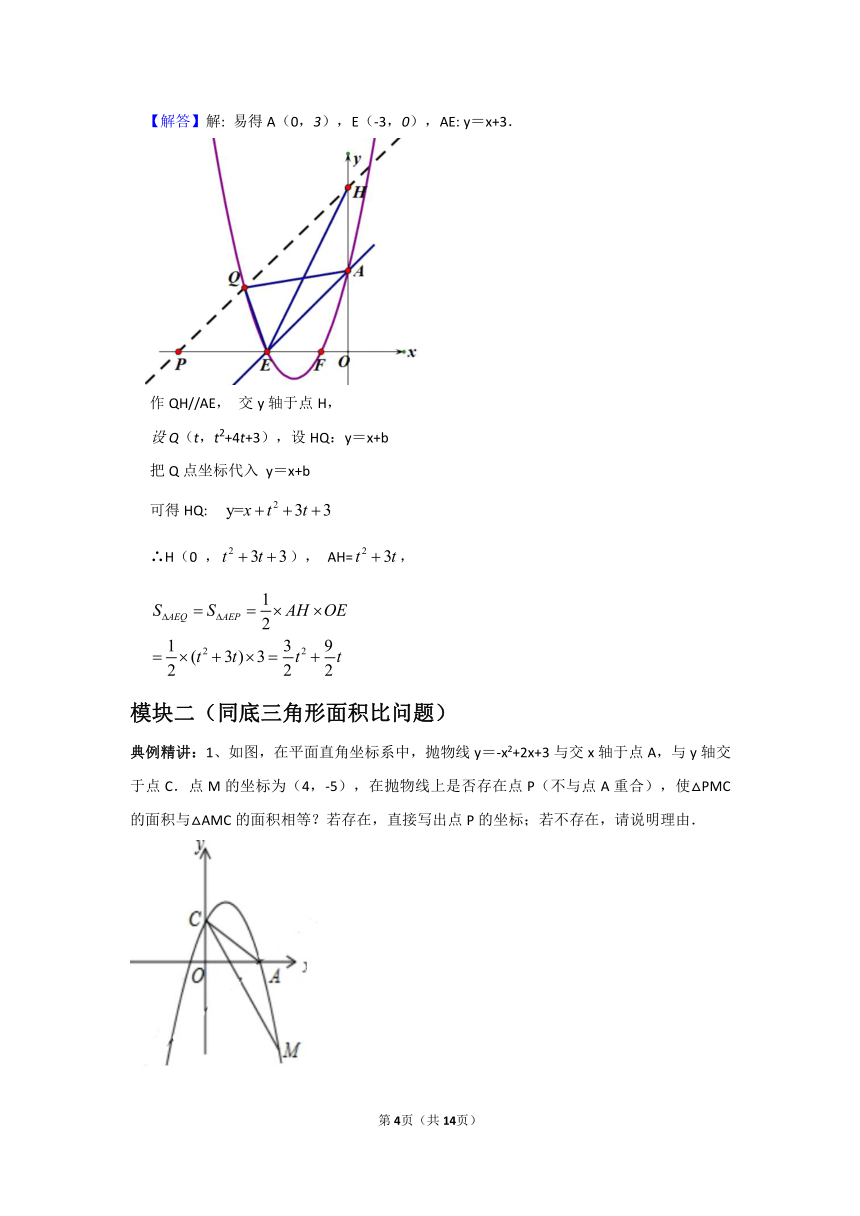
学生练习:已知:如图,抛物线y=x2+4x+3交x轴于E、F两点,交y轴于A点,若Q为抛物线上一点,连接QE,QA,设点Q的横坐标为t(t<﹣3),△QAE的面积为S,求S与t函数关系式;
【解答】解: 易得A(0,3),E(-3,0),AE: y=x+3.
作QH//AE, 交y轴于点H,
设Q(t,t2+4t+3),设HQ:y=x+b
把Q点坐标代入 y=x+b
可得HQ:
∴H(0 ,), AH=,
模块二(同底三角形面积比问题)
典例精讲:1、如图,在平面直角坐标系中,抛物线y=-x2+2x+3与交x轴于点A,与y轴交于点C.点M的坐标为(4,-5),在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
【解答】解:当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),
当x=0时,y=﹣x2+2x+3=3,则C(0,3)
设直线CM的解析式为y=mx+n,
把C(0,3),M(4,﹣5)代入得m=﹣2,n=3,
∴直线MC的解析式为y=﹣2x+3,
∵△PMC的面积与△AMC的面积相等,
∴AP∥MC,
设AP的解析式为y=﹣2x+p,
把A(3,0)代入得p=6,
∴AP的解析式为y=﹣2x+6,
解方程组得或,此时P点坐标为(1,4);
直线AP的解析式为y=﹣2x+6与y轴的交点坐标为(0,6),
∵6﹣3=3,
把直线CM向下平移3个单位得到y=﹣2x,
解方程得或,
此时P点坐标为(2+,﹣4﹣2),(2﹣,﹣4+2),
综上所述,P点坐标为(1,4)或(2+,﹣4﹣2)或(2﹣,﹣4+2),
EMBED Paint.Picture
典例精讲:2. 如图,抛物线y=﹣x2+3x+8与x轴交于点A、B点,与y轴交于点C点,P是抛物线上第一象限上的动点,连接PB,PC,当时,求点P的坐标.
解:易得A(-2,0),B(8,0), C(0,8)
作AD//BC,交y轴于D,
易求BC:y=﹣x+8
AD:y=﹣x-2,
∴CD=10,
在C点上方截取CE=6,过E作EP//BC,
交抛物线于点P,则P为所求的点
PQ:y=﹣x+14,
联立方程组,
可得点P的坐标为(2,12)或P(6,8)
模块三(利用直线与曲线相切解决面积最值问题)
例题精讲:如图,在平面直角坐标系内抛物线与x轴交于点A,点B,与y轴交于点C.过点A的直线y=x+2与抛物线交于点E.点P为第四象限内抛物线上的一个动点.在点P的运动过程中,是否存在点P使得△AEP的面积最大,若存在,请求出点P的坐标.
解:存在点P使得△AEP的面积最大,理由如下:
在直线AE的下方作MN//AE,当MN与抛物线有唯一交点P时,
此时△AEP的面积最大,P为所求的点
设MN:
联立方程组
可得
解得
联立方程组可得P(2,﹣4).此时S△APE=32,
学生练习:如图,一次函数y=﹣x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A、B两点.点P在反比例函数第三象限的图象上,使得△PAB的面积最小,求满足条件的P点坐标及△PAB面积的最小值.
【解答】解:
联立方程组可得:,
∴点B(3,1);
如图,将直线AB平移,当与双曲线第三象限的图象只有一个交点P时,此时△PAB的面积有最小值,
设平移的直线解析式为y=﹣x+b,
由题意可得:﹣x+b=,
∴x2﹣bx+3=0,
∵两图象只有一个交点,
∴Δ=b2﹣4×3=0,
∴b=±2,
∵直线y=﹣x+b与y轴交在负半轴,
∴b=﹣2,
∴平移后的解析式为y=﹣x﹣2,
∴﹣x﹣2=,
∴x=﹣,
∴y=﹣,
∴点P(﹣,﹣ ),
过点P作PH⊥AB于H,设直线y=﹣x+4与x轴交于点D,与y轴交于点C,设直线y=﹣x﹣2 与x轴交于点E,与y轴交于点F,
∴点C(0,4),点D(4,0),点E(﹣2,0),点F(0,﹣2 ),
∴CO=DO=4,EO=FO=2,
∴CD=4,EF=2,△COD和△EOF是等腰直角三角形,
∴点O到EF的距离为,点O到CD的距离为2,
∴PH=+2,
∵点A坐标为(1,3),点B(3,1),
∴AB==2,
∴△PAB面积的最小值=×2×(+2 )=2+4.
三、课后作业
1、如图,抛物线y=﹣x2+2x+3经过A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P、与BC相交于点E,连接PB.抛物线上是否存在一点Q,使△QPB与△EPB的面积相等,若存在,请求出点Q的坐标;若不存在,说明理由.
由y=﹣x2+2x+3=﹣(x﹣1)2+4,
则顶点P(1,4),对称轴为直线x=1,
∴H(1,0),
∴PH=4,BH=2,
∵B(3,0),C(0,3),
∴直线BC解析式为y=﹣x+3,
∴点E(1,2),
如图,过点E作EQ∥BC,交抛物线于Q,此时△QPB与△PEB的面积相等,
由点P、B的坐标得,直线PB的表达式为:y=﹣2(x﹣3),
则直线QE的表达式为:y=﹣2(x﹣1)+2②,
联立①②并整理得:x2﹣4x+1=0,
解得:x=2,
则点Q的坐标为(2﹣,2)或(2+,﹣2);
对于直线QE,设QE交x轴于点R,
令y=﹣2(x﹣1)+2=0,
解得:x=2,即点R(2,0),
则BR=3﹣2=1,
取点R′使BR=BR′,过点R′作PB的平行线l,如上图,则点R′(4,0),
则直线l的表达式为:y=﹣2(x﹣4),
联立y=﹣x2+2x+3和y=﹣2(x﹣4)得:x2﹣4x+5=0,
则Δ=16﹣20<0,无解,
故在点B的右侧不存在点Q,
综上,点Q的坐标为(2﹣,2)或(2+,﹣2)
2.已知二次函数与x轴交于A、B两点,A在B点的左边,与y轴交于C点,点P在第一象限的抛物线上,且在对称轴右边.S△PAC=4,求P点坐标.
如图:解当y=0时,=0,
解得x1=1,x2=3,即A(1,0),B(3,0).
当x=0时,y=2,即C(0,2)
过点P作PE∥AC,则S△PAC=S△EAC=4
设点E为(a,0)得
解得a=5,所以E(5,0)
设直线yac=kx+b,分别代入A(1,0)、C(0,2)得
解得k=-2,b=2.
所以yac=-2x+2
因为PE∥AC,所以可设ype=-2x+b代入E(5,0)得
0=-2x5+b,解得b=10
所以ype=-2x+10,联立方程组得
y=-2x+10
解得: x1=4 x2=-3
y1=2 y2=16
答:P点坐标是(4,2).
3.如图,抛物线的顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B(0,3). 抛物线上第一象限内是否存在一动点P,使S△PAB=S△CAB ,若存在,求出P点的坐标;若不存在,请说明理由。
解:易得AB:y=﹣x+3
作CD//AB,交y轴于D,可得 CD:y=﹣x+5
∴BD=2,在B点上方截取BG=,
过G作GH//AB,交抛物线于点,,
则,,即为所求的点
GH:y=﹣x+,
联立方程组,
可得点P的坐标为P(,)
4.如图,抛物线y=x2﹣4x与x轴相交于另一点A.在第一象限内与直线y=x交于点B,点E是点B关于抛物线对称轴的对称点,点F是直线OB下方的抛物线上的动点,EF与直线OB交于点G.设△BFG和△BEG的面积分别为S1和S2,求的最大值.
解:如图2,过点F作FW∥x轴交直线OB于点W,
设F(t,t2﹣4t),则W的纵坐标为t2﹣4t,
∵直线OB的解析式为y=x,
∴W(t2﹣4t,t2﹣4t),
∴WF=t﹣(t2﹣4t)=﹣t2+5t,
∵易得B(5,5),点E是点B关于抛物线对称轴直线x=2的对称点,
∴BE∥x轴,BE=6,
∴BE∥WF,
∴△WFG∽△BEG,
∴==,
∵====﹣(t﹣)2+,
∴当t=时,的最大值为.
b1
b2
y=kx+b1
y=kx
y=kx+b2
P
第2页(共14页)
《用平行线解函数中的三角形面积问题》
考点梳理:
函数与三角形面积相结合的综合题常常出现在中考的压轴题中,是中考压轴题的难点之一。主要考查学生的综合分析问题能力,考察学生数形结合思想,分类讨论思想、转化思想等。热点考题是:面积比问题,面积定值问题、面积最值问题,面积之间的和、差、比值等问题。常见的解题方法有多种,例如: 1、利用铅垂高、水平宽解决问题;2、利用割补法解决问题;3、利用面积比等于相似比的平方解决问题; 4、 利用平行线转移面积解决问题等。在二次函数与一次函数相结合的题目中求面积或者与面积相关的问题时,我们通常过三角形的某个已知顶点作对边的平行线,利用平滑定理来求解,问题就会变得简单许多,近年来,多地的中考试题中也出现了这样的题目,值得我们重视。
二、本节课学习目标:
1. 利用平行线转移三角形面积,并解决问题;
2. 利用平行线把面积比转化为线段比;
3. 通过直线与曲线相切求面积的最值;
三、新课学习:
知识铺垫:
知识铺垫:任何两条夹在平行线间的垂线段长度相等;
(1)如图1,若直线a∥b,则有MN=PQ
(2)如图2,直线a∥b,则S△ABC= S△BCD
我们先来了解什么是平滑定理:两个三角形共用同一底,且顶点都在与底平行的同一条直线上,那么由三角形的面积公式可知,这两个三角形的面积必然相等。所以平滑定理需要两个条件:(1)共底或者底在同一直线上但相等;(2)三角形的顶点都在与底平行的同一条直线上
知识铺垫2:一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行则可以推出k1=k2反之若k1=k2则可推出一次函数y=k1x+b1图像与一次函数y=k2x+b2图像平行,其中b1≠b2.
模块一(利用平行转换面积)
典例精讲: 如图,已知二次函数y=﹣x2+x+4的图象与y轴交于点A(0,4).与x轴交于点B,C,点C坐标为(8,0),连接AB、AC.若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积等于5时,求此时点N的坐标;
解法1:A(0,4),B(-2,0), C(8,0)
设NC=m,连接MC,
∵
∴
∴
∴
∵NM∥AC
∴S△AMN=S△CMN= =
∴当△AMN面积是5时,m=5,此时N点坐标为(3,0)
学生练习:已知:如图,抛物线y=x2+4x+3交x轴于E、F两点,交y轴于A点,若Q为抛物线上一点,连接QE,QA,设点Q的横坐标为t(t<﹣3),△QAE的面积为S,求S与t函数关系式;
【解答】解: 易得A(0,3),E(-3,0),AE: y=x+3.
作QH//AE, 交y轴于点H,
设Q(t,t2+4t+3),设HQ:y=x+b
把Q点坐标代入 y=x+b
可得HQ:
∴H(0 ,), AH=,
模块二(同底三角形面积比问题)
典例精讲:1、如图,在平面直角坐标系中,抛物线y=-x2+2x+3与交x轴于点A,与y轴交于点C.点M的坐标为(4,-5),在抛物线上是否存在点P(不与点A重合),使△PMC的面积与△AMC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
【解答】解:当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则A(3,0),
当x=0时,y=﹣x2+2x+3=3,则C(0,3)
设直线CM的解析式为y=mx+n,
把C(0,3),M(4,﹣5)代入得m=﹣2,n=3,
∴直线MC的解析式为y=﹣2x+3,
∵△PMC的面积与△AMC的面积相等,
∴AP∥MC,
设AP的解析式为y=﹣2x+p,
把A(3,0)代入得p=6,
∴AP的解析式为y=﹣2x+6,
解方程组得或,此时P点坐标为(1,4);
直线AP的解析式为y=﹣2x+6与y轴的交点坐标为(0,6),
∵6﹣3=3,
把直线CM向下平移3个单位得到y=﹣2x,
解方程得或,
此时P点坐标为(2+,﹣4﹣2),(2﹣,﹣4+2),
综上所述,P点坐标为(1,4)或(2+,﹣4﹣2)或(2﹣,﹣4+2),
EMBED Paint.Picture
典例精讲:2. 如图,抛物线y=﹣x2+3x+8与x轴交于点A、B点,与y轴交于点C点,P是抛物线上第一象限上的动点,连接PB,PC,当时,求点P的坐标.
解:易得A(-2,0),B(8,0), C(0,8)
作AD//BC,交y轴于D,
易求BC:y=﹣x+8
AD:y=﹣x-2,
∴CD=10,
在C点上方截取CE=6,过E作EP//BC,
交抛物线于点P,则P为所求的点
PQ:y=﹣x+14,
联立方程组,
可得点P的坐标为(2,12)或P(6,8)
模块三(利用直线与曲线相切解决面积最值问题)
例题精讲:如图,在平面直角坐标系内抛物线与x轴交于点A,点B,与y轴交于点C.过点A的直线y=x+2与抛物线交于点E.点P为第四象限内抛物线上的一个动点.在点P的运动过程中,是否存在点P使得△AEP的面积最大,若存在,请求出点P的坐标.
解:存在点P使得△AEP的面积最大,理由如下:
在直线AE的下方作MN//AE,当MN与抛物线有唯一交点P时,
此时△AEP的面积最大,P为所求的点
设MN:
联立方程组
可得
解得
联立方程组可得P(2,﹣4).此时S△APE=32,
学生练习:如图,一次函数y=﹣x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A、B两点.点P在反比例函数第三象限的图象上,使得△PAB的面积最小,求满足条件的P点坐标及△PAB面积的最小值.
【解答】解:
联立方程组可得:,
∴点B(3,1);
如图,将直线AB平移,当与双曲线第三象限的图象只有一个交点P时,此时△PAB的面积有最小值,
设平移的直线解析式为y=﹣x+b,
由题意可得:﹣x+b=,
∴x2﹣bx+3=0,
∵两图象只有一个交点,
∴Δ=b2﹣4×3=0,
∴b=±2,
∵直线y=﹣x+b与y轴交在负半轴,
∴b=﹣2,
∴平移后的解析式为y=﹣x﹣2,
∴﹣x﹣2=,
∴x=﹣,
∴y=﹣,
∴点P(﹣,﹣ ),
过点P作PH⊥AB于H,设直线y=﹣x+4与x轴交于点D,与y轴交于点C,设直线y=﹣x﹣2 与x轴交于点E,与y轴交于点F,
∴点C(0,4),点D(4,0),点E(﹣2,0),点F(0,﹣2 ),
∴CO=DO=4,EO=FO=2,
∴CD=4,EF=2,△COD和△EOF是等腰直角三角形,
∴点O到EF的距离为,点O到CD的距离为2,
∴PH=+2,
∵点A坐标为(1,3),点B(3,1),
∴AB==2,
∴△PAB面积的最小值=×2×(+2 )=2+4.
三、课后作业
1、如图,抛物线y=﹣x2+2x+3经过A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P、与BC相交于点E,连接PB.抛物线上是否存在一点Q,使△QPB与△EPB的面积相等,若存在,请求出点Q的坐标;若不存在,说明理由.
由y=﹣x2+2x+3=﹣(x﹣1)2+4,
则顶点P(1,4),对称轴为直线x=1,
∴H(1,0),
∴PH=4,BH=2,
∵B(3,0),C(0,3),
∴直线BC解析式为y=﹣x+3,
∴点E(1,2),
如图,过点E作EQ∥BC,交抛物线于Q,此时△QPB与△PEB的面积相等,
由点P、B的坐标得,直线PB的表达式为:y=﹣2(x﹣3),
则直线QE的表达式为:y=﹣2(x﹣1)+2②,
联立①②并整理得:x2﹣4x+1=0,
解得:x=2,
则点Q的坐标为(2﹣,2)或(2+,﹣2);
对于直线QE,设QE交x轴于点R,
令y=﹣2(x﹣1)+2=0,
解得:x=2,即点R(2,0),
则BR=3﹣2=1,
取点R′使BR=BR′,过点R′作PB的平行线l,如上图,则点R′(4,0),
则直线l的表达式为:y=﹣2(x﹣4),
联立y=﹣x2+2x+3和y=﹣2(x﹣4)得:x2﹣4x+5=0,
则Δ=16﹣20<0,无解,
故在点B的右侧不存在点Q,
综上,点Q的坐标为(2﹣,2)或(2+,﹣2)
2.已知二次函数与x轴交于A、B两点,A在B点的左边,与y轴交于C点,点P在第一象限的抛物线上,且在对称轴右边.S△PAC=4,求P点坐标.
如图:解当y=0时,=0,
解得x1=1,x2=3,即A(1,0),B(3,0).
当x=0时,y=2,即C(0,2)
过点P作PE∥AC,则S△PAC=S△EAC=4
设点E为(a,0)得
解得a=5,所以E(5,0)
设直线yac=kx+b,分别代入A(1,0)、C(0,2)得
解得k=-2,b=2.
所以yac=-2x+2
因为PE∥AC,所以可设ype=-2x+b代入E(5,0)得
0=-2x5+b,解得b=10
所以ype=-2x+10,联立方程组得
y=-2x+10
解得: x1=4 x2=-3
y1=2 y2=16
答:P点坐标是(4,2).
3.如图,抛物线的顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B(0,3). 抛物线上第一象限内是否存在一动点P,使S△PAB=S△CAB ,若存在,求出P点的坐标;若不存在,请说明理由。
解:易得AB:y=﹣x+3
作CD//AB,交y轴于D,可得 CD:y=﹣x+5
∴BD=2,在B点上方截取BG=,
过G作GH//AB,交抛物线于点,,
则,,即为所求的点
GH:y=﹣x+,
联立方程组,
可得点P的坐标为P(,)
4.如图,抛物线y=x2﹣4x与x轴相交于另一点A.在第一象限内与直线y=x交于点B,点E是点B关于抛物线对称轴的对称点,点F是直线OB下方的抛物线上的动点,EF与直线OB交于点G.设△BFG和△BEG的面积分别为S1和S2,求的最大值.
解:如图2,过点F作FW∥x轴交直线OB于点W,
设F(t,t2﹣4t),则W的纵坐标为t2﹣4t,
∵直线OB的解析式为y=x,
∴W(t2﹣4t,t2﹣4t),
∴WF=t﹣(t2﹣4t)=﹣t2+5t,
∵易得B(5,5),点E是点B关于抛物线对称轴直线x=2的对称点,
∴BE∥x轴,BE=6,
∴BE∥WF,
∴△WFG∽△BEG,
∴==,
∵====﹣(t﹣)2+,
∴当t=时,的最大值为.
b1
b2
y=kx+b1
y=kx
y=kx+b2
P
第2页(共14页)
同课章节目录
