深圳市中考备考百师助学培优课程——第12讲:《平行构造相似》 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第12讲:《平行构造相似》 教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 526.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 17:24:02 | ||
图片预览




文档简介
第十二讲 相似多边形相关专题3:《平行构造相似》
------蒋沅润
知识技能梳理
相似三角形是初中数学中重要的内容,应用广泛:可以证明线段的比例式;也可证明线段相等、平行、垂直等;还可计算线段的长、比值,图形面积及比值。作平行线构造成比例线段及相似三角形是常见的添加辅助线的规律,其本质是构造“A”型或“X”型图形。
学习过程
模块一:作平行线构造双A型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点D作DG∥BE,交AC于点G
易证,设CD=EG=m, 则EC=2m
又 ∴
∴
解法2 :过点E作EG∥AD,交BC于点G
易证,设EG=4m, 则AD=6m
又 ∴
∴ ∴
∴
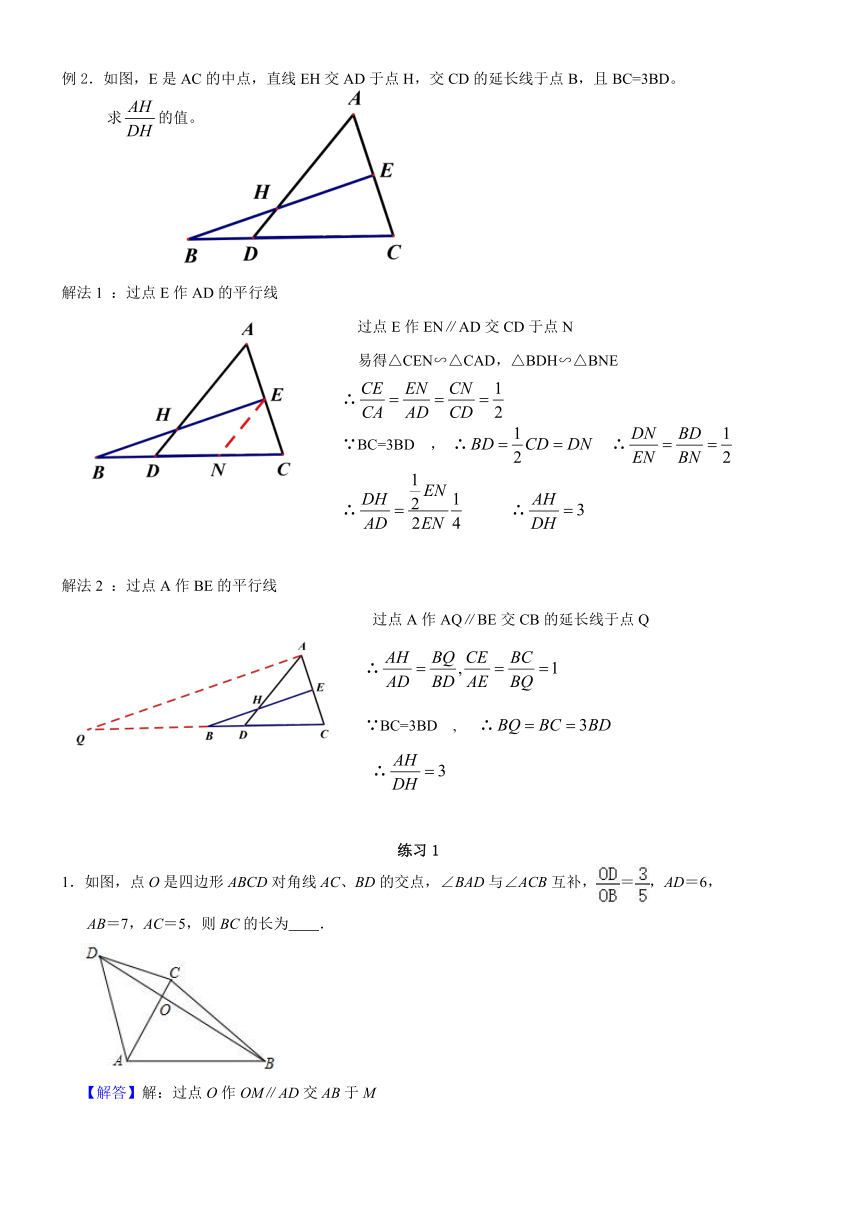
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解法1 :过点E作AD的平行线
过点E作EN∥AD交CD于点N
易得△CEN∽△CAD,△BDH∽△BNE
∴
∵BC=3BD , ∴ ∴
∴ ∴
解法2 :过点A作BE的平行线
过点A作AQ∥BE交CB的延长线于点Q
∴
∵BC=3BD , ∴
∴
练习1
如图,点O是四边形ABCD对角线AC、BD的交点,∠BAD与∠ACB互补,=,AD=6,
AB=7,AC=5,则BC的长为 .
【解答】解:过点O作OM∥AD交AB于M
∴=,
∴AM=×7=,BM=×7=,
∵△BOM∽△BDA,
∴,
∴OM=,
∵∠BAD+∠OMA=180°,∠BAD+∠ACB=180°,
∴∠OMA=∠ACB, ∴△AMO∽△ACB,
∴,
∴BC=
2.如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D,若BF=3EF,则=( )
A. B. C. D.
【解答】解:过点E作EH∥AD交BC于H,则=,
∵BE是△ABC的中线,∴CE=EA,∴CH=HD,
∵EH∥AD,∴==3,∴=,
故选:B.
如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,
AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【解答】解:如图,过点D作DF∥AE,则==,
∵=,∴DF=2EC,∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
模块二:作平行线构造双X型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点A作AG∥BC,交BE的延长线于点G。
易证,又BD=BC∴AG=BD
∴
解法2 :过点B作BG∥AC交AD的延长线于点G
易证AC=BG,
设AF=m, 则AG=4m ,AD=DG=2m
∴ ∴
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解 :过点B作AC的平行线
过点B作BM∥AC交AD延长线于点M
易得△BDM∽△CDA,△BHM∽△EHA
∴
∴
∴ ∴
∴ ∴
练习2
如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD.
【解答】解:过D作DG∥BC,交AE于G,AH于H,
∵D为AC中点,∴DH是△AFC的中位线,
∴DH=CF,CF=2DH,
∵BE=EF=CF,∴BF=2CF=4DH,
∵DG∥BC,∴==,∴QB=4DQ,
∵DG是△AEC的中位线,∴DG=CE=EF=BE,
∵DG∥BC,∴BP=PD,
∴PQ=1.5DQ,BP=2.5DQ,
∴BP:PQ:QD=5:3:2.
2.[阅读材料]
想一想在例3中,如果点D恰好是边AB的中点,那么点E是边AC的中点吗?此时,DE和BC有什么关系?△ADE与△EFC又有什么特殊关系呢? 例3如图23.3.9,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
[问题解决]
如图③,在△ABC中,P是边BC上的一点,且BP:PC=2:1,连接AP,取AP的中点M,
连接BM并延长交AC于点N,若△AMN的面积为3,则△PMB的面积为 .
【解答】
过点P作PH∥AC交BN于点H,
∵PH∥AC,∴∠PHM=∠ANM,
∵∠PMH=∠AMN,AM=PM,∴△PMH≌△AMN(AAS),
∴MH=MN,S△PMH=S△AMN=3,
∵PM∥CN,BP:PC=2:1,∴,∴,
∴S△PBH=4S△PMH=12,
∴S△PBM=S△PBH+S△PMH=12+3=15.
故答案为:15.
3 .在△ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,在BC边上以相同的速度向C运动,过点D作DE∥BC交AC于点E.运动时间为t秒.
(1)若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD.若BD=DE,求证:∠BAF=∠BCD;
(3)AF交DE于点M,在DC上取点N,使MN∥AC,连接FN.
①求证:=;
②若AB=5,BC=6,AC=4,当MN=FN时,请直接写出t的值.
【解答】解:(1)∵DE∥BC,当DF∥AC时,四边形DFCE是平行四边形.
∴,∵AD=BF=t,∴BD=5﹣t,∴,∴.
(2)证明:∵DE∥BC,∴△ADE∽△ABC,∴,
∵AD=BF,DE=DB,∴,
∵∠ABF=∠CBD,∴△ABF∽△CBD,∴∠BAF=∠BCD.
(3)①证明:∵DE∥BC,∴△ADM∽△ABF,∴,
同理得:,∴.∴,
∵MN∥EC,∴,∴.
②与①可知,FN∥AB,
∵NM=NF,∴∠NMF=∠NFM,
∵∠BAF=∠NFM,∠CAF=∠NMF,∴∠BAF=∠CAF,∴==,
∴t=BF=×6=.
模块三:做平行线构造A,X型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点D作DG∥AC,交BE于点G
证,又 ∴
∴
解法2 :过点C作CG∥AD,交BE的延长线于点G
证, ∴
∴
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解法 1 :过点C作AD的平行线
过点C作CG∥AD交BE的延长线于点G
易得△BDH∽△BCG,△AEH∽△CEG
∴
∵BC=3BD, AE = CE ∴
∴
解法2 :过点D作AC的平行线
过点D作DF∥AC交BE于点F
易得△BDF∽△BCE,△FDH∽△EAH
∴
∵BC=3BD , AE = CE
∴
练习3
如图,D、E是△ABC中BC边的两个三等分点,F是AC的中点,AD与EF交于O,
则等于( )
A. B. C. D.
【解答】解:过点F作FH∥BC交AD于G.
∵FH∥BC∴△AFG∽△ACD
∵F是AC的中点.∴==
又∵D、E是BC的分点.∴CD=DE∴=
又∵FH∥BC∴△GOF∽△DOE∴==.
故选:A.
2.如图,已知AB=AC,∠B<30°,BC上一点D,满足∠BAD=120°,,则= .
【解答】解:如图,作BE∥AC交AD于E,作BH⊥AE于H,∴△ADC∽△EDB,
∴==,∵AB=AC,∴∠ABC=∠C,∵BE∥AC,∴∠DBE=∠C,
∴∠ABC=∠DBE,
∴==,
设AB=AC=6(个单位长度),
∴BE=14,
∵∠BAD=120°,
∴∠BAH=60°,
∴AH=3,BH=3,
∴EH=AH+AE=3+AE,
在Rt△BEH中,根据勾股定理,得
∵EH2=BE2﹣BH2,
∴,
∴AE=10,
∴AD=3,
∴==.
故答案为:.
3 .抛物线y=﹣x2+2x+3与x轴交于A、B两点,点A在点B的左侧,顶点为C。点P在第一象限抛物线上,连接CP并延长交x轴于点D,连接AC,AP.若S△ACP:S△ADP=4:5,求点P的坐标;
【解答】
解法1 :
过点C作CE⊥x轴于点E,过点P作PF⊥x轴于点F
∴∠CED=∠PFD=90° ∴PF∥CE
∴△DPF∽△DCE
∴
∵ ∴
∴ ∴
∵
∴C(1,4) ∴CE=4 ∴
把 ,解得
∵点P在第一象限 ∴x>0 ∴
解法2 :
过点P作PN⊥x轴于点N,过点C作CM⊥PN于点M
∴∠CMP=∠BNP=90°
∵∠MPC=∠NPD ∴△CMP∽△DNP
∴
∵
∴ ∴
∵ ∴C(1,4)
∵CM∥y轴 ∴M与P纵坐标相同 即MN=4
∴
把 ,解得
∵点P在第一象限 ∴x>0 ∴
------蒋沅润
知识技能梳理
相似三角形是初中数学中重要的内容,应用广泛:可以证明线段的比例式;也可证明线段相等、平行、垂直等;还可计算线段的长、比值,图形面积及比值。作平行线构造成比例线段及相似三角形是常见的添加辅助线的规律,其本质是构造“A”型或“X”型图形。
学习过程
模块一:作平行线构造双A型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点D作DG∥BE,交AC于点G
易证,设CD=EG=m, 则EC=2m
又 ∴
∴
解法2 :过点E作EG∥AD,交BC于点G
易证,设EG=4m, 则AD=6m
又 ∴
∴ ∴
∴
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解法1 :过点E作AD的平行线
过点E作EN∥AD交CD于点N
易得△CEN∽△CAD,△BDH∽△BNE
∴
∵BC=3BD , ∴ ∴
∴ ∴
解法2 :过点A作BE的平行线
过点A作AQ∥BE交CB的延长线于点Q
∴
∵BC=3BD , ∴
∴
练习1
如图,点O是四边形ABCD对角线AC、BD的交点,∠BAD与∠ACB互补,=,AD=6,
AB=7,AC=5,则BC的长为 .
【解答】解:过点O作OM∥AD交AB于M
∴=,
∴AM=×7=,BM=×7=,
∵△BOM∽△BDA,
∴,
∴OM=,
∵∠BAD+∠OMA=180°,∠BAD+∠ACB=180°,
∴∠OMA=∠ACB, ∴△AMO∽△ACB,
∴,
∴BC=
2.如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D,若BF=3EF,则=( )
A. B. C. D.
【解答】解:过点E作EH∥AD交BC于H,则=,
∵BE是△ABC的中线,∴CE=EA,∴CH=HD,
∵EH∥AD,∴==3,∴=,
故选:B.
如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,
AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为 .
【解答】解:如图,过点D作DF∥AE,则==,
∵=,∴DF=2EC,∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
模块二:作平行线构造双X型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点A作AG∥BC,交BE的延长线于点G。
易证,又BD=BC∴AG=BD
∴
解法2 :过点B作BG∥AC交AD的延长线于点G
易证AC=BG,
设AF=m, 则AG=4m ,AD=DG=2m
∴ ∴
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解 :过点B作AC的平行线
过点B作BM∥AC交AD延长线于点M
易得△BDM∽△CDA,△BHM∽△EHA
∴
∴
∴ ∴
∴ ∴
练习2
如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD.
【解答】解:过D作DG∥BC,交AE于G,AH于H,
∵D为AC中点,∴DH是△AFC的中位线,
∴DH=CF,CF=2DH,
∵BE=EF=CF,∴BF=2CF=4DH,
∵DG∥BC,∴==,∴QB=4DQ,
∵DG是△AEC的中位线,∴DG=CE=EF=BE,
∵DG∥BC,∴BP=PD,
∴PQ=1.5DQ,BP=2.5DQ,
∴BP:PQ:QD=5:3:2.
2.[阅读材料]
想一想在例3中,如果点D恰好是边AB的中点,那么点E是边AC的中点吗?此时,DE和BC有什么关系?△ADE与△EFC又有什么特殊关系呢? 例3如图23.3.9,在△ABC中,DE∥BC,EF∥AB.求证:△ADE∽△EFC.
[问题解决]
如图③,在△ABC中,P是边BC上的一点,且BP:PC=2:1,连接AP,取AP的中点M,
连接BM并延长交AC于点N,若△AMN的面积为3,则△PMB的面积为 .
【解答】
过点P作PH∥AC交BN于点H,
∵PH∥AC,∴∠PHM=∠ANM,
∵∠PMH=∠AMN,AM=PM,∴△PMH≌△AMN(AAS),
∴MH=MN,S△PMH=S△AMN=3,
∵PM∥CN,BP:PC=2:1,∴,∴,
∴S△PBH=4S△PMH=12,
∴S△PBM=S△PBH+S△PMH=12+3=15.
故答案为:15.
3 .在△ABC中,点D从A出发,在AB边上以每秒一个单位的速度向B运动,同时点F从B出发,在BC边上以相同的速度向C运动,过点D作DE∥BC交AC于点E.运动时间为t秒.
(1)若AB=5,BC=6,当t为何值时,四边形DFCE为平行四边形;
(2)连接AF、CD.若BD=DE,求证:∠BAF=∠BCD;
(3)AF交DE于点M,在DC上取点N,使MN∥AC,连接FN.
①求证:=;
②若AB=5,BC=6,AC=4,当MN=FN时,请直接写出t的值.
【解答】解:(1)∵DE∥BC,当DF∥AC时,四边形DFCE是平行四边形.
∴,∵AD=BF=t,∴BD=5﹣t,∴,∴.
(2)证明:∵DE∥BC,∴△ADE∽△ABC,∴,
∵AD=BF,DE=DB,∴,
∵∠ABF=∠CBD,∴△ABF∽△CBD,∴∠BAF=∠BCD.
(3)①证明:∵DE∥BC,∴△ADM∽△ABF,∴,
同理得:,∴.∴,
∵MN∥EC,∴,∴.
②与①可知,FN∥AB,
∵NM=NF,∴∠NMF=∠NFM,
∵∠BAF=∠NFM,∠CAF=∠NMF,∴∠BAF=∠CAF,∴==,
∴t=BF=×6=.
模块三:做平行线构造A,X型
例1. 如图,在△ABC中,点D、E分别在BC、AC上,且BD=DC,,求的值。
解法1 :过点D作DG∥AC,交BE于点G
证,又 ∴
∴
解法2 :过点C作CG∥AD,交BE的延长线于点G
证, ∴
∴
例2.如图,E是AC的中点,直线EH交AD于点H,交CD的延长线于点B,且BC=3BD。
求的值。
解法 1 :过点C作AD的平行线
过点C作CG∥AD交BE的延长线于点G
易得△BDH∽△BCG,△AEH∽△CEG
∴
∵BC=3BD, AE = CE ∴
∴
解法2 :过点D作AC的平行线
过点D作DF∥AC交BE于点F
易得△BDF∽△BCE,△FDH∽△EAH
∴
∵BC=3BD , AE = CE
∴
练习3
如图,D、E是△ABC中BC边的两个三等分点,F是AC的中点,AD与EF交于O,
则等于( )
A. B. C. D.
【解答】解:过点F作FH∥BC交AD于G.
∵FH∥BC∴△AFG∽△ACD
∵F是AC的中点.∴==
又∵D、E是BC的分点.∴CD=DE∴=
又∵FH∥BC∴△GOF∽△DOE∴==.
故选:A.
2.如图,已知AB=AC,∠B<30°,BC上一点D,满足∠BAD=120°,,则= .
【解答】解:如图,作BE∥AC交AD于E,作BH⊥AE于H,∴△ADC∽△EDB,
∴==,∵AB=AC,∴∠ABC=∠C,∵BE∥AC,∴∠DBE=∠C,
∴∠ABC=∠DBE,
∴==,
设AB=AC=6(个单位长度),
∴BE=14,
∵∠BAD=120°,
∴∠BAH=60°,
∴AH=3,BH=3,
∴EH=AH+AE=3+AE,
在Rt△BEH中,根据勾股定理,得
∵EH2=BE2﹣BH2,
∴,
∴AE=10,
∴AD=3,
∴==.
故答案为:.
3 .抛物线y=﹣x2+2x+3与x轴交于A、B两点,点A在点B的左侧,顶点为C。点P在第一象限抛物线上,连接CP并延长交x轴于点D,连接AC,AP.若S△ACP:S△ADP=4:5,求点P的坐标;
【解答】
解法1 :
过点C作CE⊥x轴于点E,过点P作PF⊥x轴于点F
∴∠CED=∠PFD=90° ∴PF∥CE
∴△DPF∽△DCE
∴
∵ ∴
∴ ∴
∵
∴C(1,4) ∴CE=4 ∴
把 ,解得
∵点P在第一象限 ∴x>0 ∴
解法2 :
过点P作PN⊥x轴于点N,过点C作CM⊥PN于点M
∴∠CMP=∠BNP=90°
∵∠MPC=∠NPD ∴△CMP∽△DNP
∴
∵
∴ ∴
∵ ∴C(1,4)
∵CM∥y轴 ∴M与P纵坐标相同 即MN=4
∴
把 ,解得
∵点P在第一象限 ∴x>0 ∴
同课章节目录
