深圳市中考备考百师助学培优课程——第16讲:对角互补模型 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第16讲:对角互补模型 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 00:00:00 | ||
图片预览


文档简介
教学设计
课 题 第十六讲《对角互补模型----全等、相似、圆》 课时 课 型 复习
教学目标 经历对角互补模型有特殊到一般的探索过程,发展学生的合情推理能力;探索并证明的过程,培养学生的逻辑素养,利用模型的三个模块体会数学分类讨论,转化,化归,类比等数学思想在数学中的应用。
教学重点 理解并掌握构建全等三角形和相似三角形解决几何问题。
教学难点 应用构建图形的方式解决几何问题。
教学方法 自主学习,合作探究式学习
课前准备 自主学习单,直尺,三角板,圆规
教学过程 师生活动
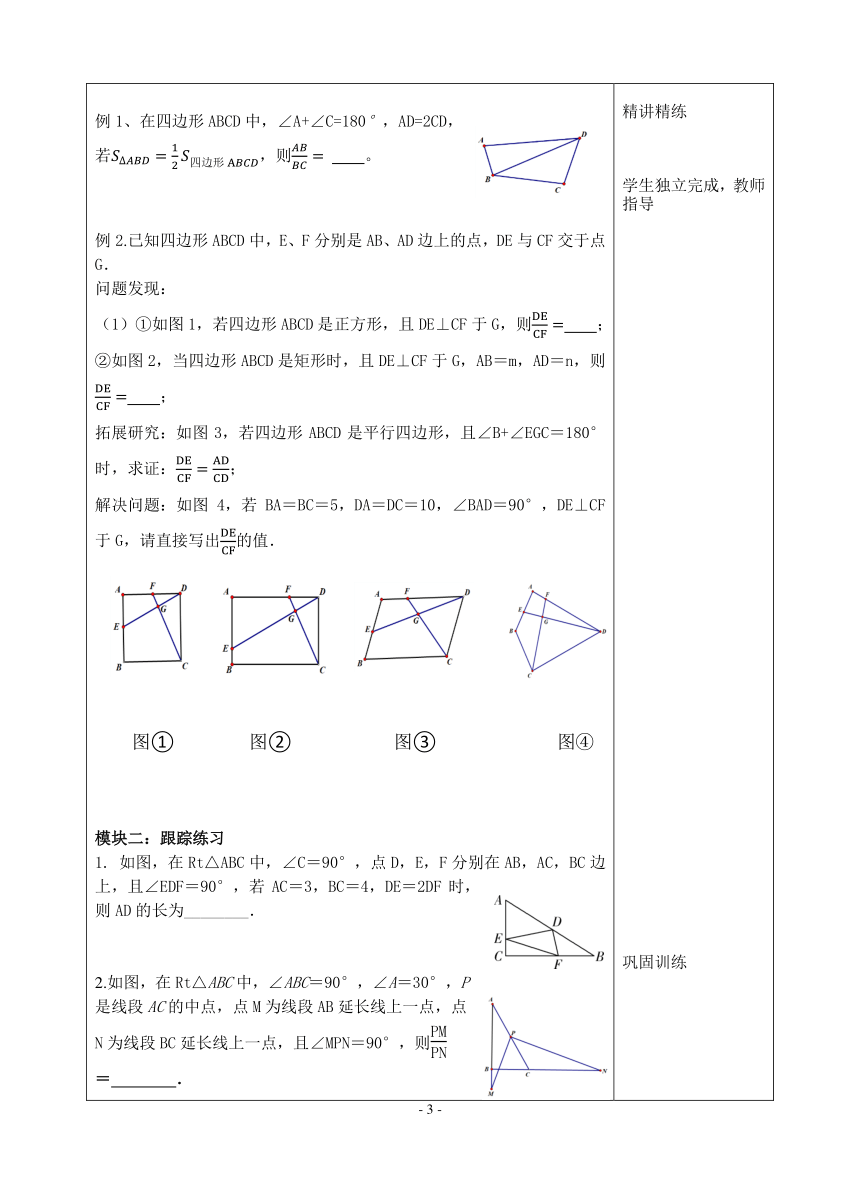
模块一:全等型 典例精讲:如图,已知OC平分∠AOB,, 的两边分别与OA交于点D,OB交于点E,试探究以下结论: ((1)当, (①CD与CE的数量关系为 ; ②OD、OE与OC之间的数量关系为 ; ③与OC之间的数量关系为 ; ((2)当,以上关系式是否还成立?若不成立写出关系式,并说明理由。 ((3)当为任意锐角时,请用含有的式子表示 ①CD与CE的数量关系为 ; ②OD、OE与OC之间的数量关系为 ; ③与OC之间的数量关系为 ; 例1.如图,在四边形ABCD中,CA平分,∠BAD=60°,∠BCD=120°,连接AC,若四边形ABCD的面积为 ,则AC= 。 例2.已知:如图①,在四边形ABCD中,=DB平分 求证:AB=BC 如图②,若试判断形状,并说明理由。 如图③,在(2)的条件下,在AB上取一点E,BC上取一点F,连接CE,AF,并交于点M,连接EF。若AD=EF=7,CD=8(CF),求AE的长。 图① 图② 图③ 【归纳总结】对角互补的四边形中,有一条对角线是角平分线时,可以构造全等三角形来解决边,角和面积问题。 模块一:跟踪练习 在正方形ABCD中,AB=4,点E在对角线BD上,连接AE,过点E作EF⊥AE,交BC于点F。若BF=1,则 。 2.矩形ABCD,AB=6,AD=5,G为CD中点,DE=DG,于F,则DF的长为 。 3.如图,在正方形ABCD中,,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作,交线段AB于点N.连接NC交BD于点G.若,则的值为________. 模块二:相似型 模块二:典例精讲 如图,已知∠AOB=90 ,OC为∠AOB内部一条射线, ∠DCE=90 ,交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan 例1、在四边形ABCD中,∠A+∠C=180,AD=2CD, 若,则 。 例2.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G. 问题发现: (1)①如图1,若四边形ABCD是正方形,且DE⊥CF于G,则 ; ②如图2,当四边形ABCD是矩形时,且DE⊥CF于G,AB=m,AD=n,则 ; 拓展研究:如图3,若四边形ABCD是平行四边形,且∠B+∠EGC=180°时,求证:; 解决问题:如图4,若BA=BC=5,DA=DC=10,∠BAD=90°,DE⊥CF于G,请直接写出的值. 图① 图② 图③ 图④ 模块二:跟踪练习 如图,在Rt△ABC中,∠C=90°,点D,E,F分别在AB,AC,BC边上,且∠EDF=90°,若AC=3,BC=4,DE=2DF时,则AD的长为________. 2.如图,在Rt△ABC中,∠ABC=90°,∠A=30°,P是线段AC的中点,点M为线段AB延长线上一点,点N为线段BC延长线上一点,且∠MPN=90°,则= . 3.问题情境:如图1,在正方形ABCD中,点E是对角线AC上一点,连接BE,过点E分别作AC,BE的垂线,分别交直线BC,CD于点F,G.试猜想线段BF和CG的数量关系,并加以证明. (1)数学思考:请解答上述问题. (2)问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若,,求的值. (3)问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积. 【归纳总结】对角互补的四边形中,有一组邻边成比例,可以构造相似三角形来解决问题。
模块三:四点共圆--综合题 模块三:典例精讲 已知:如图,在四边形ABCD中,已知∠A=∠C=90°,求证A、B、C、D四点共圆. 归纳:当∠A+∠C=180°时,可以得出点A,B,C,D四点共圆。 【例1】.如图,正方形 ABCD,点 P 是对角线 AC 上一点,连接 BP,过 P 作 PQ⊥BP,PQ 交 CD 于 Q,连接 BQ 交 AC 于 G,若 AP,Q 为 CD 中点,则下列结论: ①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形 ABCD 的面积是16;其中正确结论的个数是( ) A.4 B.3 C.2 D.1 模块三:跟踪练习 如图,点 M、N 分别是正方形 ABCD 的边 BC,CD 上的动点(不与B, C,D 重合),且始终保持∠MAN=45,AM,AN 分别交 BD于点 E,F,以下四个结论:①AF⊥FM;②;③当∠BAM=22.5°时,∠FMN=∠BAM;④DN+BM=MN.其中正确的有( ) A.4个 B.3个 C.2个 D.1个 2、已知:在正方形 ABCD 中,点 E 是边 AB 上点,点 G 在边 AD 上,连接 EG,EG=DG,作 EF⊥EG,交边 BC 于点 F(图1). 求证:AE+CF=EF; (2)连接正方形 ABCD 的对角线 AC,连接 DF,线段 AC 与线段 DF 相交于点 K(图2),探究线段 AE、AD、AK 之间的数量关系,直接写出你的结论; (3)在(2)的条件下,连接线段 DE 与线段 AC 相交于点 P,(图3)若 AK=. △BEF 的周长为24,求 PK 的长. 图1 图2 图3 3.(2022 广州越秀区) (1)【基础巩固】如图1,△ABC内接于⊙O,若∠C=60°,弦AB=2,则半径r= ; (2)【问题探究】如图2,四边形ABCD内接于⊙O,若∠ADC=60°,AD=DC,点B为弧AC上一动点(不与点A,点C重合). 求证:AB+BC=BD; (3)【解决问题】如图3,一块空地由三条直路(线段AD、AB、BC)和一条道路劣弧围成,已知CM=DM千米,∠DMC=60°,的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点M处,另外三个入口分别在点C、D、P处,其中点P在上,并在公园中修四条慢跑道,即图中的线段DM、MC、CP、PD,是否存在一种规划方案,使得四条慢跑道总长度(即四边形DMCP的周长)最大?若存在,求其最大值;若不存在,说明理由. 【总结提升】 今天你有哪些收获? 作业:完成自主学习单 学生自主探究 当, 时,写出结论,并说明理由 师生共同归纳,为任意锐角时,三种数量关系。 师生共同探究归纳方法 精讲精练 巩固训练 师生共同探究对角互补的四边形,一组邻边成比例时的边角关系。 精讲精练 学生独立完成,教师指导 巩固训练 师生共同归纳总结方法 利用四边形中一组对角是90时,可以证明这四个顶点在同一个圆上,由特殊到一般可以归纳出当四边形对角互补时,这四个顶点是在同一个圆上的。 精讲精练 巩固训练 师生共同总结归纳
板书设计: 对角互补四边形 模块一:全等型 例题: 模块二:相似型 练习: 模块三:四点共圆
教后反思:
课 题 第十六讲《对角互补模型----全等、相似、圆》 课时 课 型 复习
教学目标 经历对角互补模型有特殊到一般的探索过程,发展学生的合情推理能力;探索并证明的过程,培养学生的逻辑素养,利用模型的三个模块体会数学分类讨论,转化,化归,类比等数学思想在数学中的应用。
教学重点 理解并掌握构建全等三角形和相似三角形解决几何问题。
教学难点 应用构建图形的方式解决几何问题。
教学方法 自主学习,合作探究式学习
课前准备 自主学习单,直尺,三角板,圆规
教学过程 师生活动
模块一:全等型 典例精讲:如图,已知OC平分∠AOB,, 的两边分别与OA交于点D,OB交于点E,试探究以下结论: ((1)当, (①CD与CE的数量关系为 ; ②OD、OE与OC之间的数量关系为 ; ③与OC之间的数量关系为 ; ((2)当,以上关系式是否还成立?若不成立写出关系式,并说明理由。 ((3)当为任意锐角时,请用含有的式子表示 ①CD与CE的数量关系为 ; ②OD、OE与OC之间的数量关系为 ; ③与OC之间的数量关系为 ; 例1.如图,在四边形ABCD中,CA平分,∠BAD=60°,∠BCD=120°,连接AC,若四边形ABCD的面积为 ,则AC= 。 例2.已知:如图①,在四边形ABCD中,=DB平分 求证:AB=BC 如图②,若试判断形状,并说明理由。 如图③,在(2)的条件下,在AB上取一点E,BC上取一点F,连接CE,AF,并交于点M,连接EF。若AD=EF=7,CD=8(CF),求AE的长。 图① 图② 图③ 【归纳总结】对角互补的四边形中,有一条对角线是角平分线时,可以构造全等三角形来解决边,角和面积问题。 模块一:跟踪练习 在正方形ABCD中,AB=4,点E在对角线BD上,连接AE,过点E作EF⊥AE,交BC于点F。若BF=1,则 。 2.矩形ABCD,AB=6,AD=5,G为CD中点,DE=DG,于F,则DF的长为 。 3.如图,在正方形ABCD中,,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作,交线段AB于点N.连接NC交BD于点G.若,则的值为________. 模块二:相似型 模块二:典例精讲 如图,已知∠AOB=90 ,OC为∠AOB内部一条射线, ∠DCE=90 ,交OA边于点D,交OB边于点E,∠BOC=. 求证:CE=CD tan 例1、在四边形ABCD中,∠A+∠C=180,AD=2CD, 若,则 。 例2.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G. 问题发现: (1)①如图1,若四边形ABCD是正方形,且DE⊥CF于G,则 ; ②如图2,当四边形ABCD是矩形时,且DE⊥CF于G,AB=m,AD=n,则 ; 拓展研究:如图3,若四边形ABCD是平行四边形,且∠B+∠EGC=180°时,求证:; 解决问题:如图4,若BA=BC=5,DA=DC=10,∠BAD=90°,DE⊥CF于G,请直接写出的值. 图① 图② 图③ 图④ 模块二:跟踪练习 如图,在Rt△ABC中,∠C=90°,点D,E,F分别在AB,AC,BC边上,且∠EDF=90°,若AC=3,BC=4,DE=2DF时,则AD的长为________. 2.如图,在Rt△ABC中,∠ABC=90°,∠A=30°,P是线段AC的中点,点M为线段AB延长线上一点,点N为线段BC延长线上一点,且∠MPN=90°,则= . 3.问题情境:如图1,在正方形ABCD中,点E是对角线AC上一点,连接BE,过点E分别作AC,BE的垂线,分别交直线BC,CD于点F,G.试猜想线段BF和CG的数量关系,并加以证明. (1)数学思考:请解答上述问题. (2)问题解决:如图2,在图1的条件下,将“正方形ABCD”改为“矩形ABCD”,其他条件不变.若,,求的值. (3)问题拓展:在(2)的条件下,当点E为AC的中点时,请直接写出的面积. 【归纳总结】对角互补的四边形中,有一组邻边成比例,可以构造相似三角形来解决问题。
模块三:四点共圆--综合题 模块三:典例精讲 已知:如图,在四边形ABCD中,已知∠A=∠C=90°,求证A、B、C、D四点共圆. 归纳:当∠A+∠C=180°时,可以得出点A,B,C,D四点共圆。 【例1】.如图,正方形 ABCD,点 P 是对角线 AC 上一点,连接 BP,过 P 作 PQ⊥BP,PQ 交 CD 于 Q,连接 BQ 交 AC 于 G,若 AP,Q 为 CD 中点,则下列结论: ①∠PBC=∠PQD;②BP=PQ;③∠BPC=∠BQC;④正方形 ABCD 的面积是16;其中正确结论的个数是( ) A.4 B.3 C.2 D.1 模块三:跟踪练习 如图,点 M、N 分别是正方形 ABCD 的边 BC,CD 上的动点(不与B, C,D 重合),且始终保持∠MAN=45,AM,AN 分别交 BD于点 E,F,以下四个结论:①AF⊥FM;②;③当∠BAM=22.5°时,∠FMN=∠BAM;④DN+BM=MN.其中正确的有( ) A.4个 B.3个 C.2个 D.1个 2、已知:在正方形 ABCD 中,点 E 是边 AB 上点,点 G 在边 AD 上,连接 EG,EG=DG,作 EF⊥EG,交边 BC 于点 F(图1). 求证:AE+CF=EF; (2)连接正方形 ABCD 的对角线 AC,连接 DF,线段 AC 与线段 DF 相交于点 K(图2),探究线段 AE、AD、AK 之间的数量关系,直接写出你的结论; (3)在(2)的条件下,连接线段 DE 与线段 AC 相交于点 P,(图3)若 AK=. △BEF 的周长为24,求 PK 的长. 图1 图2 图3 3.(2022 广州越秀区) (1)【基础巩固】如图1,△ABC内接于⊙O,若∠C=60°,弦AB=2,则半径r= ; (2)【问题探究】如图2,四边形ABCD内接于⊙O,若∠ADC=60°,AD=DC,点B为弧AC上一动点(不与点A,点C重合). 求证:AB+BC=BD; (3)【解决问题】如图3,一块空地由三条直路(线段AD、AB、BC)和一条道路劣弧围成,已知CM=DM千米,∠DMC=60°,的半径为1千米,市政府准备将这块空地规划为一个公园,主入口在点M处,另外三个入口分别在点C、D、P处,其中点P在上,并在公园中修四条慢跑道,即图中的线段DM、MC、CP、PD,是否存在一种规划方案,使得四条慢跑道总长度(即四边形DMCP的周长)最大?若存在,求其最大值;若不存在,说明理由. 【总结提升】 今天你有哪些收获? 作业:完成自主学习单 学生自主探究 当, 时,写出结论,并说明理由 师生共同归纳,为任意锐角时,三种数量关系。 师生共同探究归纳方法 精讲精练 巩固训练 师生共同探究对角互补的四边形,一组邻边成比例时的边角关系。 精讲精练 学生独立完成,教师指导 巩固训练 师生共同归纳总结方法 利用四边形中一组对角是90时,可以证明这四个顶点在同一个圆上,由特殊到一般可以归纳出当四边形对角互补时,这四个顶点是在同一个圆上的。 精讲精练 巩固训练 师生共同总结归纳
板书设计: 对角互补四边形 模块一:全等型 例题: 模块二:相似型 练习: 模块三:四点共圆
教后反思:
同课章节目录
