不等式——高一数学北师大版(2019)必修一课时优化训练(含解析)
文档属性
| 名称 | 不等式——高一数学北师大版(2019)必修一课时优化训练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
不等式——高一数学北师大版(2019)必修一课时优化训练
一、选择题
1.已知,则的最大值为( )
A. B. C. D.3
2.若直线过点,则的最小值等于( )
A.2 B.3 C.4 D.5
3.正数a,b满足,若不等式对任意实数x恒成立,则实数m的取值范围是( )
A. B. C. D.
4.已知a,b均为正实数,且满足,则的最小值为( )
A.2 B. C. D.
5.一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员先将的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.若顾客实际购得的黄金为,则( )
A. B. C. D.以上都有可能
6.已知a,b为正实数,且,则的最小值为( )
A. B. C. D.
7.已知a,b为正实数,且,则ab的取值范围是( )
A. B. C. D.
8.已知,则取得最大值时x的值为( )
A. B. C. D.
二、多项选择题
9.已知,若对任意的,不等式恒成立.则( )
A. B.
C.的最小值为12 D.的最小值为
10.已知正数a,b满足,,则( )
A. B. C. D.
11.下列各式中,最小值是2的为( )
A. B.
C. D.
12.下列函数中,最小值是4的函数有( )
A.
B.
C.
D.
三、填空题
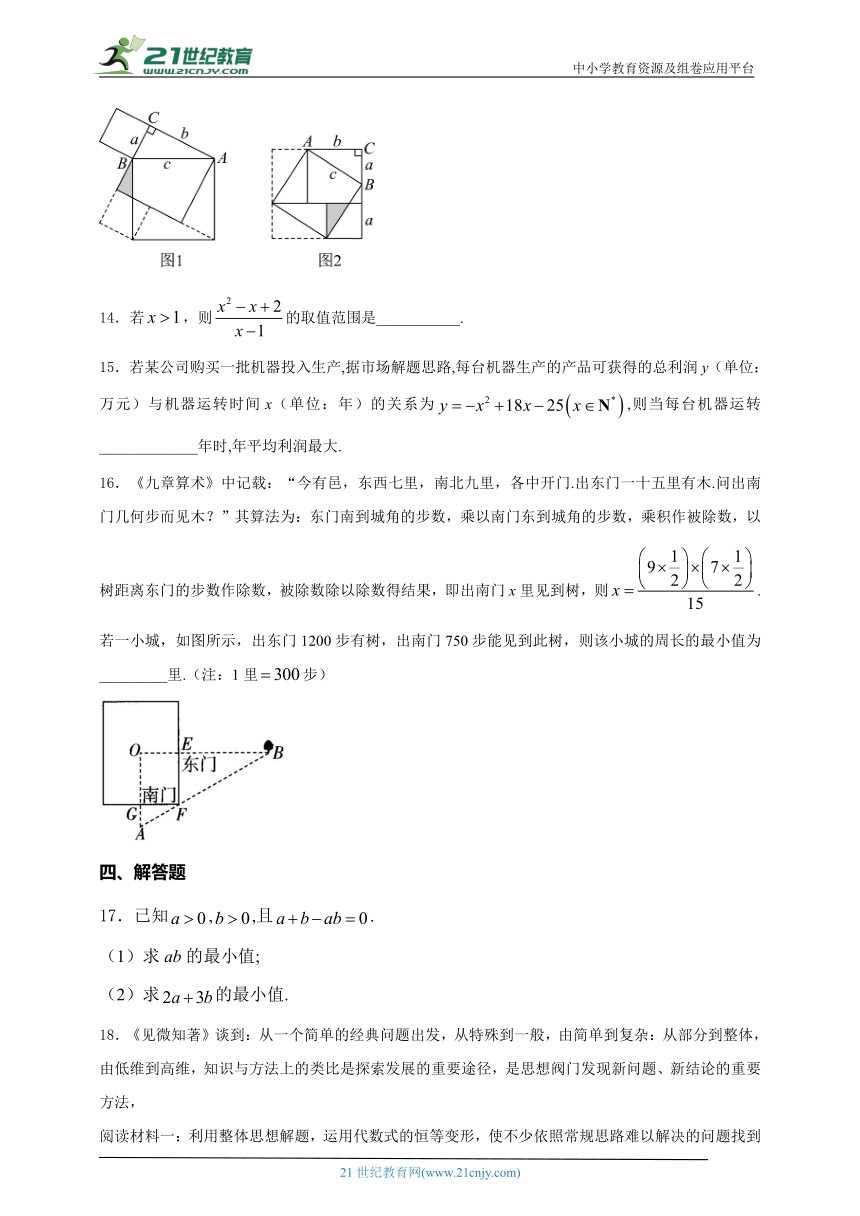
13.出入相补是指一个平面(或立体)图形被分割成若干部分后面积(或体积)的总和保持不变,我国汉代数学家构造弦图,利用出入相补原理证明了勾股定理,我国清代的梅文鼎、李锐、华蘅芳、何梦瑶等都通过出入相补原理创造了不同的面积证法证明了勾股定理.在下面两个图中,若,,,图中两个阴影三角形的周长分别为,,则的最小值为________.
14.若,则的取值范围是___________.
15.若某公司购买一批机器投入生产,据市场解题思路,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为,则当每台机器运转_____________年时,年平均利润最大.
16.《九章算术》中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木?”其算法为:东门南到城角的步数,乘以南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门x里见到树,则.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为_________里.(注:1里步)
四、解答题
17.已知,,且.
(1)求ab的最小值;
(2)求的最小值.
18.《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法,
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如,,求证:.
证明:原式.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如,求___________.
(2)若,解方程.
(3)若正数a、b满足,求的最小值.
19.通过前面一个月的学习,大家认识了一个朋友:基本不等式.即当时有(当且仅当时不等式取“=”).我们称为正数a,b的算术平均数,为它们的几何平均数,两个正数的算术平均数不小于他们的几何平均数.这只是均值不等式的一个简化版本.均值不等式的历史可以追溯到19世纪,由Chebycheff在1882年发表的论文中首次提出.均值不等式,也称为平均值不等式或平均不等式,是数学中的一个重要公式.它的基本形式包括调和平均数、几何平均数、算术平均数和平方平均数之间的关系.它表明:n个正数,,,…,的算术平均数不小于它们的几何平均数,且当,,,…,,这些数全部相等时,算术平均数与几何平均数相等.
(1)写出时算术平均数与几何平均数之间的关系,并写出取等号的条件(无需证明);
(2)利用你写出的式子,求的最小值;
(3)如图,把一块长为6的正方形铁片的各角切去大小相同的小正方形,再将它的边沿虚线折转做成一个无盖的方底盒子.问切去的正方形边长是多少时,才能使盒子的容积最大
20.已知a,b,满足,则的最小值为________.
参考答案
1.答案:B
解析:由题意得,,即,
当且仅当,即,或,时等号成立,
所以的最大值为.
故选:B.
2.答案:C
解析:直线过点,,
则,
当且仅当时取等号.
故答案为:C.
3.答案:A
解析:,
,且a,b为正数,
,
当且仅当,即时,,
若不等式对任意实数x恒成立,
则对任意实数x恒成立,
即对任意实数x恒成立,
,
,
故选:A
4.答案:B
解析:因为a,b均为正实数,且,得,
所以,
又,
当且仅当即时取等号,所以.
故选:B.
5.答案:A
解析:由于天平两臂不等长,可设天平左臂长为a,右臂长为b,则,
再设先称得黄金为,后称得黄金为,则,,
,,
,
当且仅当,即时等号成立,但,等号不成立,即.
因此,顾客购得的黄金.
故选:A.
6.答案:D
解析:正实数a,b满足,则,当且仅当,即时取等号,所以的最小值为.故选D.
7.答案:D
解析:因为a,b为正实数,所以,即,所以或,所以(当且仅当时等号成立)或(当且仅当时等号成立).所以ab的取值范围是,故选D.
8.答案:D
解析:,
则由基本不等式得,,
当且仅当,即时,等号成立,
故取得最大值时x的值为
故选:D.
9.答案:ACD
解析:因为,
恒成立,即恒成立,
因为,所以当时,,则需,
当时,,则需,
故当时,,即,
所以且,故选项A正确,选项B错误;
所以,
当且仅当时,即时取等,故选项C正确;
因为,
令,
当且仅当,即时等号成立,故,
所以,故,
所以在上,单调递减,即,
所以,故选项D正确.
故选:ACD.
10.答案:ABD
解析:由,,得,即,又,,所以,A正确;显然,当且仅当时取等号,则,当且仅当时等号同时成立,B正确;取,,满足,,此时,C错误;由,得,即,于是,同理,则,D正确.故选ABD.
11.答案:AC
解析:对于A选项,对于,因为,所以.
根据基本不等式,这里,.
则,当且仅当,即时等号成立,所以A选项最小值是2.
对于B选项,对于,设,则.
根据基本不等式,当且仅当即时等号成立.
但,等号取不到,所以B选项最小值不是2.
对于C选项,对于,因为.
根据基本不等式,当且仅当,即时等号成立,所以C选项最小值是.
对于D选项,对于,因为,则..
根据基本不等式,当且仅当即时等号成立.
所以,D选项最小值不是2.
故选:AC.
12.答案:ACD
解析:对A,,可得,当时取等,故A正确,
对B,,,故B错误,
对C,,,
当取等,故C正确,
对D,,,当时取等,故D正确.
故选:ACD
13.答案:
解析:如图1,易知,且,
所以,所以;
如图2,易知,且,
所以,所以,
所以,
又因为,所以,当且仅当时取等号,
所以,
所以最小值为,
故答案为:.
14.答案:
解析:因为,所以,故,当且仅当,即时取等号,即的取值范围是.
15.答案:5
解析:每台机器运转x年的平均利润为,且,
由基本不等式可得,当且仅当时等号成立,
所以,当且仅当时等号成立,
所以当每台机器运转5年时,年平均利润最大,最大值为8万元.
故答案为:5.
16.答案:
解析:1里步,由题图可知,步里,步里,,,且,,,则,该小城的周长为(里),当且仅当里时等号成立.故该小城的周长的最小值为里.
17.答案:(1)4
(2)
解析:(1)因为,所以,所以,
所以,所以,当且仅当即时等号成立,即ab的最小值为;
(2),
当且仅当即即,时,等号成立,
所以的最小值为.
18.答案:(1)1
(2)
(3)
解析:(1)由题意得.
(2)
原方程可化为:,
即:,
,
即,解得:.
(3)由题意得
,
当且仅当,即时,等号成立,
有最小值,此时有最大值,
从而有最小值,
即有最小值.
19.答案:(1)答案见解析
(2)3
(3)切去的正方形边长为1时,才能使盒子的容积最大,
解析:(1)由题意,当时,若,,,可得,
即算术平均数与几何平均数的关系为,当且仅当时,等号成立.
(2)由(1)中,当,,,可得,
可得时,,
当且仅当时,即时,等号成立,
所以的最小值为3.
(3)设小正方形的边长为x,则盒子高为,底边边长为,
可得盒子的容积为,其中,
则,
当且仅当时,即时,等号成立,
所以切去的正方形边长为1时,才能使盒子的容积最大,最大容积为16.
20.答案:1
解析:正数a,b,c,,
则
,当且仅当时取等号,
所以的最小值为1.
故答案为:1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
不等式——高一数学北师大版(2019)必修一课时优化训练
一、选择题
1.已知,则的最大值为( )
A. B. C. D.3
2.若直线过点,则的最小值等于( )
A.2 B.3 C.4 D.5
3.正数a,b满足,若不等式对任意实数x恒成立,则实数m的取值范围是( )
A. B. C. D.
4.已知a,b均为正实数,且满足,则的最小值为( )
A.2 B. C. D.
5.一家商店使用一架两臂不等长的天平称黄金.一位顾客到店里购买黄金,售货员先将的砝码放在天平左盘中,取出一些黄金放在天平右盘中使天平平衡;再将的砝码放在天平右盘中,再取出一些黄金放在天平左盘中使天平平衡;最后将两次称得的黄金交给顾客.若顾客实际购得的黄金为,则( )
A. B. C. D.以上都有可能
6.已知a,b为正实数,且,则的最小值为( )
A. B. C. D.
7.已知a,b为正实数,且,则ab的取值范围是( )
A. B. C. D.
8.已知,则取得最大值时x的值为( )
A. B. C. D.
二、多项选择题
9.已知,若对任意的,不等式恒成立.则( )
A. B.
C.的最小值为12 D.的最小值为
10.已知正数a,b满足,,则( )
A. B. C. D.
11.下列各式中,最小值是2的为( )
A. B.
C. D.
12.下列函数中,最小值是4的函数有( )
A.
B.
C.
D.
三、填空题
13.出入相补是指一个平面(或立体)图形被分割成若干部分后面积(或体积)的总和保持不变,我国汉代数学家构造弦图,利用出入相补原理证明了勾股定理,我国清代的梅文鼎、李锐、华蘅芳、何梦瑶等都通过出入相补原理创造了不同的面积证法证明了勾股定理.在下面两个图中,若,,,图中两个阴影三角形的周长分别为,,则的最小值为________.
14.若,则的取值范围是___________.
15.若某公司购买一批机器投入生产,据市场解题思路,每台机器生产的产品可获得的总利润y(单位:万元)与机器运转时间x(单位:年)的关系为,则当每台机器运转_____________年时,年平均利润最大.
16.《九章算术》中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木?”其算法为:东门南到城角的步数,乘以南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门x里见到树,则.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为_________里.(注:1里步)
四、解答题
17.已知,,且.
(1)求ab的最小值;
(2)求的最小值.
18.《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是思想阀门发现新问题、新结论的重要方法,
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(1)整体观察;(2)整体设元;(3)整体代入:(4)整体求和等.
例如,,求证:.
证明:原式.
波利亚在《怎样解题》中指出:“当你找到第一个藤菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征.
请根据阅读材料解答下列问题
(1)已知如,求___________.
(2)若,解方程.
(3)若正数a、b满足,求的最小值.
19.通过前面一个月的学习,大家认识了一个朋友:基本不等式.即当时有(当且仅当时不等式取“=”).我们称为正数a,b的算术平均数,为它们的几何平均数,两个正数的算术平均数不小于他们的几何平均数.这只是均值不等式的一个简化版本.均值不等式的历史可以追溯到19世纪,由Chebycheff在1882年发表的论文中首次提出.均值不等式,也称为平均值不等式或平均不等式,是数学中的一个重要公式.它的基本形式包括调和平均数、几何平均数、算术平均数和平方平均数之间的关系.它表明:n个正数,,,…,的算术平均数不小于它们的几何平均数,且当,,,…,,这些数全部相等时,算术平均数与几何平均数相等.
(1)写出时算术平均数与几何平均数之间的关系,并写出取等号的条件(无需证明);
(2)利用你写出的式子,求的最小值;
(3)如图,把一块长为6的正方形铁片的各角切去大小相同的小正方形,再将它的边沿虚线折转做成一个无盖的方底盒子.问切去的正方形边长是多少时,才能使盒子的容积最大
20.已知a,b,满足,则的最小值为________.
参考答案
1.答案:B
解析:由题意得,,即,
当且仅当,即,或,时等号成立,
所以的最大值为.
故选:B.
2.答案:C
解析:直线过点,,
则,
当且仅当时取等号.
故答案为:C.
3.答案:A
解析:,
,且a,b为正数,
,
当且仅当,即时,,
若不等式对任意实数x恒成立,
则对任意实数x恒成立,
即对任意实数x恒成立,
,
,
故选:A
4.答案:B
解析:因为a,b均为正实数,且,得,
所以,
又,
当且仅当即时取等号,所以.
故选:B.
5.答案:A
解析:由于天平两臂不等长,可设天平左臂长为a,右臂长为b,则,
再设先称得黄金为,后称得黄金为,则,,
,,
,
当且仅当,即时等号成立,但,等号不成立,即.
因此,顾客购得的黄金.
故选:A.
6.答案:D
解析:正实数a,b满足,则,当且仅当,即时取等号,所以的最小值为.故选D.
7.答案:D
解析:因为a,b为正实数,所以,即,所以或,所以(当且仅当时等号成立)或(当且仅当时等号成立).所以ab的取值范围是,故选D.
8.答案:D
解析:,
则由基本不等式得,,
当且仅当,即时,等号成立,
故取得最大值时x的值为
故选:D.
9.答案:ACD
解析:因为,
恒成立,即恒成立,
因为,所以当时,,则需,
当时,,则需,
故当时,,即,
所以且,故选项A正确,选项B错误;
所以,
当且仅当时,即时取等,故选项C正确;
因为,
令,
当且仅当,即时等号成立,故,
所以,故,
所以在上,单调递减,即,
所以,故选项D正确.
故选:ACD.
10.答案:ABD
解析:由,,得,即,又,,所以,A正确;显然,当且仅当时取等号,则,当且仅当时等号同时成立,B正确;取,,满足,,此时,C错误;由,得,即,于是,同理,则,D正确.故选ABD.
11.答案:AC
解析:对于A选项,对于,因为,所以.
根据基本不等式,这里,.
则,当且仅当,即时等号成立,所以A选项最小值是2.
对于B选项,对于,设,则.
根据基本不等式,当且仅当即时等号成立.
但,等号取不到,所以B选项最小值不是2.
对于C选项,对于,因为.
根据基本不等式,当且仅当,即时等号成立,所以C选项最小值是.
对于D选项,对于,因为,则..
根据基本不等式,当且仅当即时等号成立.
所以,D选项最小值不是2.
故选:AC.
12.答案:ACD
解析:对A,,可得,当时取等,故A正确,
对B,,,故B错误,
对C,,,
当取等,故C正确,
对D,,,当时取等,故D正确.
故选:ACD
13.答案:
解析:如图1,易知,且,
所以,所以;
如图2,易知,且,
所以,所以,
所以,
又因为,所以,当且仅当时取等号,
所以,
所以最小值为,
故答案为:.
14.答案:
解析:因为,所以,故,当且仅当,即时取等号,即的取值范围是.
15.答案:5
解析:每台机器运转x年的平均利润为,且,
由基本不等式可得,当且仅当时等号成立,
所以,当且仅当时等号成立,
所以当每台机器运转5年时,年平均利润最大,最大值为8万元.
故答案为:5.
16.答案:
解析:1里步,由题图可知,步里,步里,,,且,,,则,该小城的周长为(里),当且仅当里时等号成立.故该小城的周长的最小值为里.
17.答案:(1)4
(2)
解析:(1)因为,所以,所以,
所以,所以,当且仅当即时等号成立,即ab的最小值为;
(2),
当且仅当即即,时,等号成立,
所以的最小值为.
18.答案:(1)1
(2)
(3)
解析:(1)由题意得.
(2)
原方程可化为:,
即:,
,
即,解得:.
(3)由题意得
,
当且仅当,即时,等号成立,
有最小值,此时有最大值,
从而有最小值,
即有最小值.
19.答案:(1)答案见解析
(2)3
(3)切去的正方形边长为1时,才能使盒子的容积最大,
解析:(1)由题意,当时,若,,,可得,
即算术平均数与几何平均数的关系为,当且仅当时,等号成立.
(2)由(1)中,当,,,可得,
可得时,,
当且仅当时,即时,等号成立,
所以的最小值为3.
(3)设小正方形的边长为x,则盒子高为,底边边长为,
可得盒子的容积为,其中,
则,
当且仅当时,即时,等号成立,
所以切去的正方形边长为1时,才能使盒子的容积最大,最大容积为16.
20.答案:1
解析:正数a,b,c,,
则
,当且仅当时取等号,
所以的最小值为1.
故答案为:1
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
