5.2 函数的表示方法 练习(含解析)-2024-2025学年高一上学期数学苏教版(2019)必修第一册
文档属性
| 名称 | 5.2 函数的表示方法 练习(含解析)-2024-2025学年高一上学期数学苏教版(2019)必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 120.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-12 21:26:25 | ||
图片预览


文档简介
5.2 函数的表示方法
一、选择题
1.设f(x)=2x+3,g(x)=f(x-2),则g(x)= ( )
A.2x+1 B.2x-1
C.2x-3 D.2x+7
2.已知函数f(x)由下表给出,则f[f(3)]等于 ( )
x 1 2 3 4
f(x) 3 2 4 1
A.1 B.2 C.3 D.4
3.若g(x)=1-2x,f[g(x)]=,则f的值为 ( )
A.1 B.15 C.4 D.30
4.(多选题)如图所示的图象表示的函数的解析式可以为 ( )
A.y=|x-1|(0≤x≤2)
B.y=-|x-1|(0≤x≤2)
C.y=-|x-1|(0≤x≤2)
D.y=
5.某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了a km,觉得有点累,休息后沿原路返回b km(bA B C D
6.设函数f(x)=若f(a)+f(-1)=2,则a= ( )
A.-3 B.±3
C.-1 D.±1
7.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为 ( )
A.y= B.y=
C.y= D.y=
8.(多选题)已知函数f(x)的图象由如图所示的两条线段组成,则 ( )
A.f[f(1)]=3
B.f(2)>f(0)
C.f(x)=-x+1+2|x-1|,x∈[0,4]
D.存在a>0,使得不等式f(x)≤a的解集为
9.(多选题)已知函数f(x)=则 ( )
A.f(0)=2
B.f(x)的值域为(-∞,4)
C.f(x)<1的解集为(-∞,-1)∪(-1,1)
D.若f(x)=3,则x=或1
二、填空题
10.若f(+1)=x+2,则f(x)= .
11.已知f(x)=则f(2)= ;不等式f(x)>f(1)的解集为 .
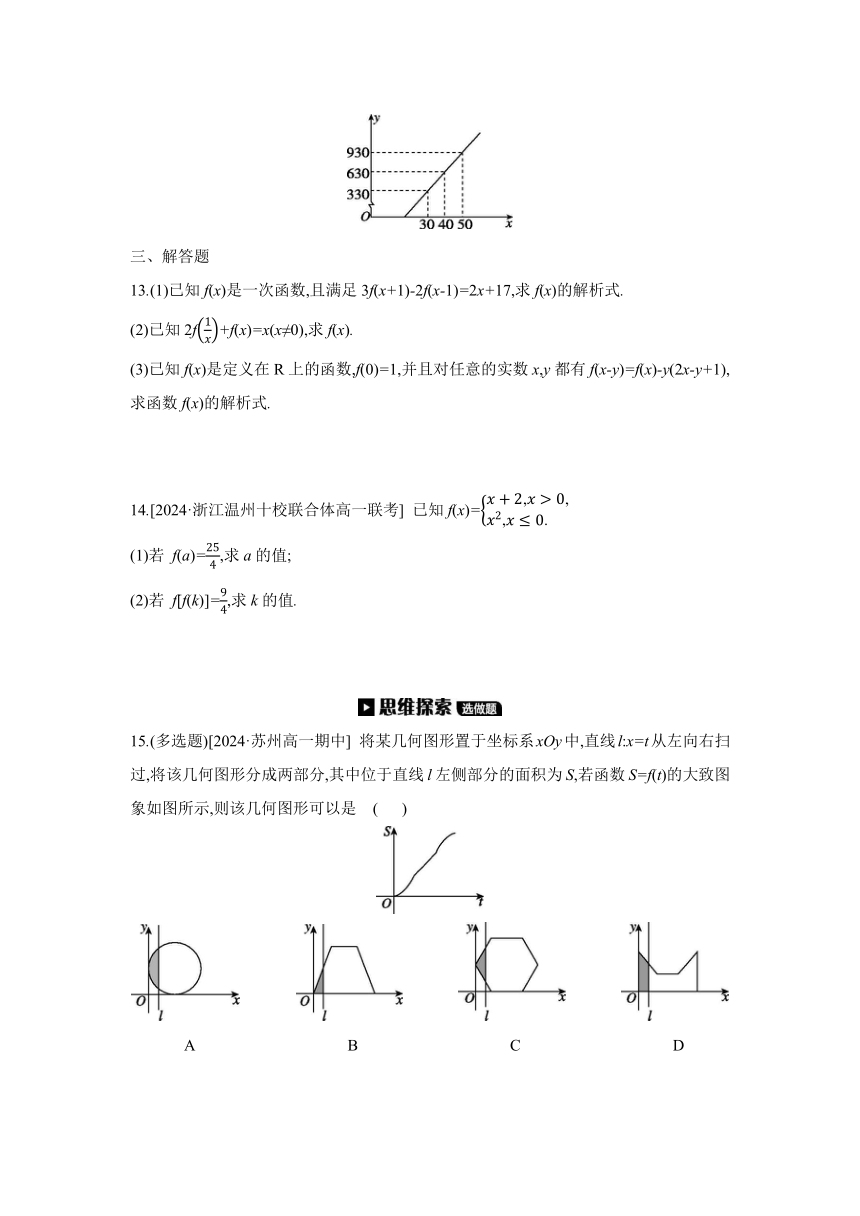
12.某航空公司规定,乘客所携带行李的运费y(元)与其重量x(kg)之间的关系由如图的一次函数图象确定,那么乘客可免费携带行李的最大重量为 kg.
三、解答题
13.(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x)的解析式.
(2)已知2f+f(x)=x(x≠0),求f(x).
(3)已知f(x)是定义在R上的函数,f(0)=1,并且对任意的实数x,y都有f(x-y)=f(x)-y(2x-y+1),求函数f(x)的解析式.
14.[2024·浙江温州十校联合体高一联考] 已知f(x)=
(1)若 f(a)=,求a的值;
(2)若 f[f(k)]=,求k的值.
15.(多选题)[2024·苏州高一期中] 将某几何图形置于坐标系xOy中,直线l:x=t从左向右扫过,将该几何图形分成两部分,其中位于直线l左侧部分的面积为S,若函数S=f(t)的大致图象如图所示,则该几何图形可以是 ( )
A B C D
16.如图所示,在边长为4的正方形ABCD上有一点P,点P沿着折线BCDA由B点(起点)向A点(终点)移动.设P点移动的路程为x(0(1)求f(x)的函数解析式;
(2)作出函数f(x)的图象,并根据图象求f(x)的最大值.
5.2 函数的表示方法
1.B [解析] ∵f(x)=2x+3,∴f(x-2)=2(x-2)+3=2x-1,即g(x)=2x-1,故选B.
2.A [解析] ∵f(3)=4,∴f[f(3)]=f(4)=1.
3.B [解析] 由g(x)=1-2x=,得x=,所以f==15.故选B.
4.BD [解析] 当0≤x≤1时,y=x;当15.C [解析] 由题意知,第一段时间内与起点的距离越来越大,第二段时间内与起点的距离不变,第三段时间内与起点的距离越来越小,第四段时间内与起点的距离越来越大.所以图象C合适.故选C.
6.D [解析] 若a≥0,则+1=2,得a=1;若a<0,则+1=2,得a=-1.
7.B [解析] 方法一:取特殊值法,若x=56,则y=5,排除C,D,若x=57,则y=6,排除A,故选B.
方法二:设x=10m+α(0≤α≤9),当0≤α≤6时,==m=;当6<α≤9时,==m+1=+1.故选B.
8.AC [解析] 因为f(1)=0,f(0)=3,所以f[f(1)]=f(0)=3,故A正确.因为f(0)=3,00,使得不等式f(x)≤a的解集为,故D错误.故选AC.
9.BC [解析] 对于A,f(0)=02=0,A错误.对于B,当x≤-1时,f(x)=x+2≤-1+2=1;当-110.(x-1)2+2(x≥1) [解析] 令t=+1,则t≥1,x=(t-1)2,f(t)=(t-1)2+2,故f(x)=(x-1)2+2(x≥1).
11.5 (-2,0)∪(1,+∞) [解析] f(2)=22+2-1=5.f(x)>f(1)等价于 或解得-21,故f(x)>f(1)的解集为(-2,0)∪(1,+∞).
12.19 [解析] 设一次函数的解析式为y=ax+b(a≠0),代入(30,330)与(40,630),得解得
即y=30x-570,若要免费,则y≤0,∴x≤19.
13.解:(1)由题设f(x)=ax+b(a≠0),则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b,即ax+5a+b=2x+17恒成立,
∴解得∴f(x)=2x+7.
(2)由f(x)+2f=x,得f+2f(x)=.
于是得到关于f(x)的方程组解得f(x)=-(x≠0).
(3)令y=x,则f(x-x)=f(0)=f(x)-x(2x-x+1)=1,所以f(x)=x2+x+1.
14.解:(1)当a>0时,由f(a)=a+2=, 得a=;
当a≤0时,由f(a)=a2=,解得a=(舍)或a=-.
所以a=或a=-.
(2)令f(k)=t,则f(t)=.当t>0时,由f(t)=t+2=,得t=,所以f(k)=.
当k>0时,由f(k)=k+2=,得k=-(舍);
当k≤0时,由f(k)=k2=,解得k=-或k=(舍).
当t≤0时,由f(t)=t2=,解得t=(舍)或t=-.
当k>0时,由f(k)=k+2=-,得k=-(舍);
当k≤0时,f(k)=k2=-无实数解.
综上所述,k=-.
15.BC [解析] 由已知图象可知面积S的增速经历三种变化,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小.对于A选项,由圆的性质可知,面积S的增速先越来越大,后越来越小,A选项错误;对于B选项,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小,B选项正确;对于C选项,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小,C选项正确;对于D选项,首先面积S的增速越来越小,之后面积S匀速增加,最后面积S的增速越来越大,D选项错误.故选BC.
16.解:(1)函数f(x)的定义域为(0,12).
当0当8∴函数解析式为f(x)=
(2)函数f(x)的图象如图所示.由图象可知f(x)max=8.
一、选择题
1.设f(x)=2x+3,g(x)=f(x-2),则g(x)= ( )
A.2x+1 B.2x-1
C.2x-3 D.2x+7
2.已知函数f(x)由下表给出,则f[f(3)]等于 ( )
x 1 2 3 4
f(x) 3 2 4 1
A.1 B.2 C.3 D.4
3.若g(x)=1-2x,f[g(x)]=,则f的值为 ( )
A.1 B.15 C.4 D.30
4.(多选题)如图所示的图象表示的函数的解析式可以为 ( )
A.y=|x-1|(0≤x≤2)
B.y=-|x-1|(0≤x≤2)
C.y=-|x-1|(0≤x≤2)
D.y=
5.某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了a km,觉得有点累,休息后沿原路返回b km(b
6.设函数f(x)=若f(a)+f(-1)=2,则a= ( )
A.-3 B.±3
C.-1 D.±1
7.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为 ( )
A.y= B.y=
C.y= D.y=
8.(多选题)已知函数f(x)的图象由如图所示的两条线段组成,则 ( )
A.f[f(1)]=3
B.f(2)>f(0)
C.f(x)=-x+1+2|x-1|,x∈[0,4]
D.存在a>0,使得不等式f(x)≤a的解集为
9.(多选题)已知函数f(x)=则 ( )
A.f(0)=2
B.f(x)的值域为(-∞,4)
C.f(x)<1的解集为(-∞,-1)∪(-1,1)
D.若f(x)=3,则x=或1
二、填空题
10.若f(+1)=x+2,则f(x)= .
11.已知f(x)=则f(2)= ;不等式f(x)>f(1)的解集为 .
12.某航空公司规定,乘客所携带行李的运费y(元)与其重量x(kg)之间的关系由如图的一次函数图象确定,那么乘客可免费携带行李的最大重量为 kg.
三、解答题
13.(1)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x)的解析式.
(2)已知2f+f(x)=x(x≠0),求f(x).
(3)已知f(x)是定义在R上的函数,f(0)=1,并且对任意的实数x,y都有f(x-y)=f(x)-y(2x-y+1),求函数f(x)的解析式.
14.[2024·浙江温州十校联合体高一联考] 已知f(x)=
(1)若 f(a)=,求a的值;
(2)若 f[f(k)]=,求k的值.
15.(多选题)[2024·苏州高一期中] 将某几何图形置于坐标系xOy中,直线l:x=t从左向右扫过,将该几何图形分成两部分,其中位于直线l左侧部分的面积为S,若函数S=f(t)的大致图象如图所示,则该几何图形可以是 ( )
A B C D
16.如图所示,在边长为4的正方形ABCD上有一点P,点P沿着折线BCDA由B点(起点)向A点(终点)移动.设P点移动的路程为x(0
(2)作出函数f(x)的图象,并根据图象求f(x)的最大值.
5.2 函数的表示方法
1.B [解析] ∵f(x)=2x+3,∴f(x-2)=2(x-2)+3=2x-1,即g(x)=2x-1,故选B.
2.A [解析] ∵f(3)=4,∴f[f(3)]=f(4)=1.
3.B [解析] 由g(x)=1-2x=,得x=,所以f==15.故选B.
4.BD [解析] 当0≤x≤1时,y=x;当1
6.D [解析] 若a≥0,则+1=2,得a=1;若a<0,则+1=2,得a=-1.
7.B [解析] 方法一:取特殊值法,若x=56,则y=5,排除C,D,若x=57,则y=6,排除A,故选B.
方法二:设x=10m+α(0≤α≤9),当0≤α≤6时,==m=;当6<α≤9时,==m+1=+1.故选B.
8.AC [解析] 因为f(1)=0,f(0)=3,所以f[f(1)]=f(0)=3,故A正确.因为f(0)=3,0
9.BC [解析] 对于A,f(0)=02=0,A错误.对于B,当x≤-1时,f(x)=x+2≤-1+2=1;当-1
11.5 (-2,0)∪(1,+∞) [解析] f(2)=22+2-1=5.f(x)>f(1)等价于 或解得-2
12.19 [解析] 设一次函数的解析式为y=ax+b(a≠0),代入(30,330)与(40,630),得解得
即y=30x-570,若要免费,则y≤0,∴x≤19.
13.解:(1)由题设f(x)=ax+b(a≠0),则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b,即ax+5a+b=2x+17恒成立,
∴解得∴f(x)=2x+7.
(2)由f(x)+2f=x,得f+2f(x)=.
于是得到关于f(x)的方程组解得f(x)=-(x≠0).
(3)令y=x,则f(x-x)=f(0)=f(x)-x(2x-x+1)=1,所以f(x)=x2+x+1.
14.解:(1)当a>0时,由f(a)=a+2=, 得a=;
当a≤0时,由f(a)=a2=,解得a=(舍)或a=-.
所以a=或a=-.
(2)令f(k)=t,则f(t)=.当t>0时,由f(t)=t+2=,得t=,所以f(k)=.
当k>0时,由f(k)=k+2=,得k=-(舍);
当k≤0时,由f(k)=k2=,解得k=-或k=(舍).
当t≤0时,由f(t)=t2=,解得t=(舍)或t=-.
当k>0时,由f(k)=k+2=-,得k=-(舍);
当k≤0时,f(k)=k2=-无实数解.
综上所述,k=-.
15.BC [解析] 由已知图象可知面积S的增速经历三种变化,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小.对于A选项,由圆的性质可知,面积S的增速先越来越大,后越来越小,A选项错误;对于B选项,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小,B选项正确;对于C选项,首先面积S的增速越来越大,之后面积S匀速增加,最后面积S的增速越来越小,C选项正确;对于D选项,首先面积S的增速越来越小,之后面积S匀速增加,最后面积S的增速越来越大,D选项错误.故选BC.
16.解:(1)函数f(x)的定义域为(0,12).
当0
(2)函数f(x)的图象如图所示.由图象可知f(x)max=8.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
