第六章 圆 第2节 与圆有关的位置关系 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 第六章 圆 第2节 与圆有关的位置关系 学案(含答案)2025年中考数学人教版一轮复习考点探究 |
|
|
| 格式 | docx | ||
| 文件大小 | 230.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 08:25:48 | ||
图片预览




文档简介
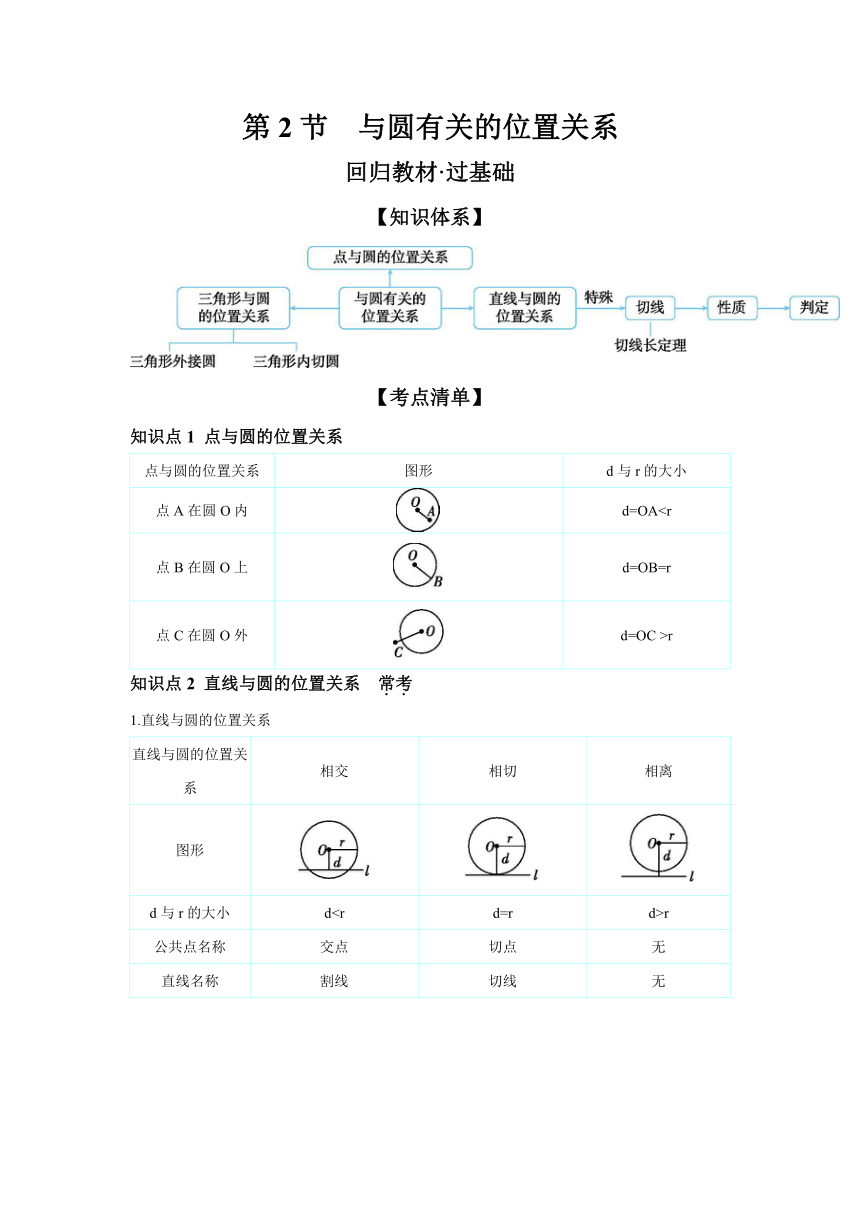
第2节 与圆有关的位置关系
回归教材·过基础
【知识体系】
【考点清单】
知识点1 点与圆的位置关系
点与圆的位置关系 图形 d与r的大小
点A在圆O内 d=OA点B在圆O上 d=OB=r
点C在圆O外 d=OC >r
知识点2 直线与圆的位置关系 常考
1.直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
图形
d与r的大小 dr
公共点名称 交点 切点 无
直线名称 割线 切线 无
2.切线的性质与判定
性质定理 圆的切线垂直于过切点的半径
推论 1.经过圆心且垂直于切线的直线必过切点
2.经过切点且垂直于切线的直线必过圆心
切线的判定 1.和圆有且只有一个公共点的直线是圆的切线
2.如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
3.经过半径的外端并且垂直于这条半径的直线是圆的切线
3.切线长定理
(1)切线长:如图,过圆外一点P,有两条直线PM,PN分别与☉O相切,点P和切点之间线段的长叫作这点到圆的切线长.
(2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分两条切线的夹角.
知识点3 三角形的内心和外心
1.三角形的外心:三角形外接圆的圆心叫作三角形的外心.三角形的外心是三角形三边垂直平分线的交点,它到三角形三个顶点的距离相等.
2.三角形的内心:三角形内切圆的圆心叫作三角形的内心.三角形的内心是三角形三条角平分线的交点,它到三角形三边的距离相等,且在三角形内部.
【基础演练】
1.如图,在△ABC中,∠ACB=90°,AB=10,BC=8.以点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外时,r的值可能是 ( )
A.6 B.8 C.10 D.12
2.如图,这是“光盘行动”的宣传海报,图中筷子与餐盘可看成直线和圆,它们的位置关系是 ( )
A.相切 B.相交 C.相离 D.平行
3.平面内,☉O的半径为5,若直线l与☉O相离,则圆心O到直线l的距离可能是 ( )
A.6 B.5 C.4 D.3
4.(2024·三明二模)如图,在△ABC中,AB=AC,边BC与☉A相切于点D,边AB,AC与☉A分别交于点M,N.求证:=.
真题精粹·重变式
1.(2024·福建)如图,已知点A,B在☉O上,∠AOB=72°,直线MN与☉O相切,切点为C,且C为的中点,则∠ACM等于 ( )
A.18°
B.30°
C.36°
D.72°
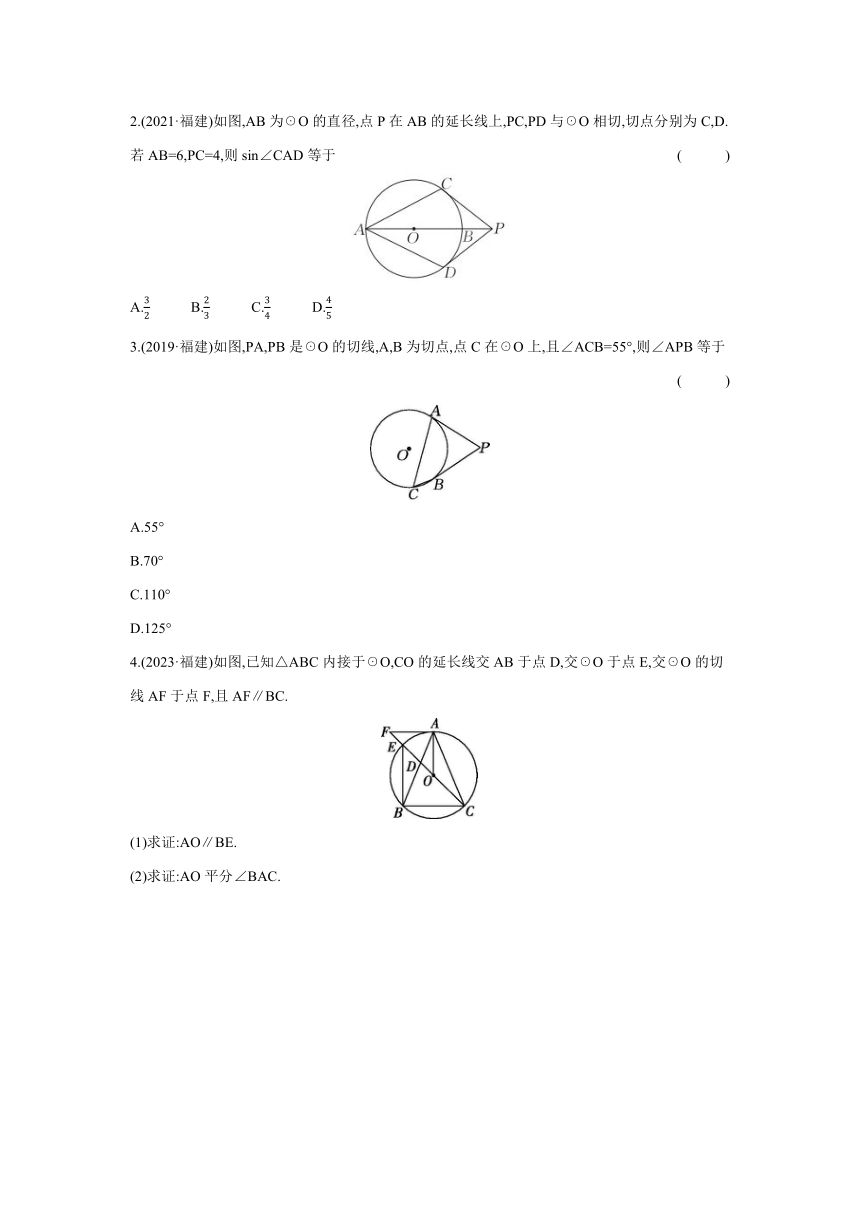
2.(2021·福建)如图,AB为☉O的直径,点P在AB的延长线上,PC,PD与☉O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于 ( )
A. B. C. D.
3.(2019·福建)如图,PA,PB是☉O的切线,A,B为切点,点C在☉O上,且∠ACB=55°,则∠APB等于 ( )
A.55°
B.70°
C.110°
D.125°
4.(2023·福建)如图,已知△ABC内接于☉O,CO的延长线交AB于点D,交☉O于点E,交☉O的切线AF于点F,且AF∥BC.
(1)求证:AO∥BE.
(2)求证:AO平分∠BAC.
5.(2020·福建)如图,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与点B,D重合的点,sin A=.
(1)求∠BED的度数.
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF与☉O相切.
核心突破·拓思维
考点 切线的判定
如图,在△ABC中,CA=CB,O为AB上一点.以O为圆心,OB长为半径的☉O过点C,交AB于另一点D,若D是OA的中点,求证:AC是☉O的切线.
由CA=CB 可得∠A=∠B
可证△AOC≌△BDC ∠ACO=∠BCD=90°
即可得AC是☉O的切线
核心方法
证明直线与圆相切常见情形
(1)已知半径,证垂直;(2)已知垂直,证半径;(3)半径、垂直都不知,作垂线试一试.
如图,△ABC内接于☉O,AB是☉O的直径,∠A=60°.点E在AB延长线上,BE=OB.过点E作ED⊥AC,交AC的延长线于点D. 求证:DE是☉O的切线.
如图,△ABC为☉O内接三角形,∠B=2∠A,点M为直径AB上一点,过点M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF 是☉O 的切线.
(2)设☉O 的半径为2,且AC=CE,求AM 的长.
参考答案
回归教材·过基础
基础演练
1.B 2.B 3.A
4.证明:连接AD,如图所示.
∵BC与☉A相切于点D,
∴AD⊥BC.
∵AB=AC,
∴∠BAD=∠CAD,
∴=.
真题精粹·重变式
1.A 2.D 3.B
4.证明:(1)∵AF是☉O的切线,
∴AF⊥OA,即∠OAF=90°.
∵CE是☉O的直径,
∴∠CBE=90°,∴∠OAF=∠CBE.
∵AF∥BC,∴∠BAF=∠ABC,
∴∠OAF-∠BAF=∠CBE-∠ABC,
即∠OAB=∠ABE,
∴AO∥BE.
(2)∵∠ABE与∠ACE都是所对的圆周角,
∴∠ABE=∠ACE.
∵OA=OC,∴∠ACE=∠OAC,
∴∠ABE=∠OAC,
由(1)知∠OAB=∠ABE,
∴∠OAB=∠OAC,
∴AO平分∠BAC.
5.解析:(1)如图1,连接OB.
图1
∵AB与☉O相切于点B,
∴∠ABO=90°.
∵sin A=,
∴∠A=30°,∴∠BOD=∠ABO+∠A=120°,
∴∠BED=∠BOD=60°.
(2)证明:如图2,连接OF,OB.
图2
∵AB是切线,∴∠OBF=90°.
∵BF=3,OB=3,
∴tan∠BOF==,∴∠BOF=60°.
∵∠BOD=120°,
∴∠BOF=∠DOF=60°.
在△BOF和△DOF中,
∴△BOF≌△DOF(SAS),
∴∠OBF=∠ODF=90°,∴DF与☉O相切.
核心突破·拓思维
例 证明:如图,连接OC,CD.
∵CA=CB,
∴∠A=∠B.
∵BD是直径,
∴∠BCD=90°.
∵D是OA的中点,
∴AD=OD.
又OB=OD,∴AO=BD,
∴△AOC≌△BDC(SAS),
∴∠ACO=∠BCD=90°,∴OC⊥AC.
∵C为半径OC的外端点,
∴AC是☉O的切线.
变式1 证明:如图,过点O作OF⊥DE于点F.
∵ED⊥AC,
∴∠D=90°.
又∵∠A=60°,
∴∠E=30°,
∴OF=OE.
∵BE=OB,
∴OB=OE,
∴OF=OB,则点F在☉O上,
∴DE是☉O的切线.
变式2 解析:(1)证明:如图,连接OC.
∵AB是☉O的直径,
∴∠ACB=90°.
又∵∠B=2∠A,
∴∠B=60°,∠A=30°,
∵EM⊥AB,∴∠EMB=90°.
在Rt△EMB中,∠B=60°,∴∠E=30°.
又∵EF=FC,∴∠ECF=∠E=30°.
又∵∠ECA=90°,∴∠FCA=60°.
∵OA=OC,∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,∴FC是☉O的切线.
(2)在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,AC=BC=2.
∵AC=CE,∴CE=2,
∴BE=BC+CE=2+2.
在Rt△BEM中,∠BME=90°,∠E=30°,
∴BM=BE=1+,
∴AM=AB-BM=4-1-=3-.
回归教材·过基础
【知识体系】
【考点清单】
知识点1 点与圆的位置关系
点与圆的位置关系 图形 d与r的大小
点A在圆O内 d=OA
点C在圆O外 d=OC >r
知识点2 直线与圆的位置关系 常考
1.直线与圆的位置关系
直线与圆的位置关系 相交 相切 相离
图形
d与r的大小 d
公共点名称 交点 切点 无
直线名称 割线 切线 无
2.切线的性质与判定
性质定理 圆的切线垂直于过切点的半径
推论 1.经过圆心且垂直于切线的直线必过切点
2.经过切点且垂直于切线的直线必过圆心
切线的判定 1.和圆有且只有一个公共点的直线是圆的切线
2.如果圆心到一条直线的距离等于圆的半径,那么这条直线是圆的切线
3.经过半径的外端并且垂直于这条半径的直线是圆的切线
3.切线长定理
(1)切线长:如图,过圆外一点P,有两条直线PM,PN分别与☉O相切,点P和切点之间线段的长叫作这点到圆的切线长.
(2)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分两条切线的夹角.
知识点3 三角形的内心和外心
1.三角形的外心:三角形外接圆的圆心叫作三角形的外心.三角形的外心是三角形三边垂直平分线的交点,它到三角形三个顶点的距离相等.
2.三角形的内心:三角形内切圆的圆心叫作三角形的内心.三角形的内心是三角形三条角平分线的交点,它到三角形三边的距离相等,且在三角形内部.
【基础演练】
1.如图,在△ABC中,∠ACB=90°,AB=10,BC=8.以点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外时,r的值可能是 ( )
A.6 B.8 C.10 D.12
2.如图,这是“光盘行动”的宣传海报,图中筷子与餐盘可看成直线和圆,它们的位置关系是 ( )
A.相切 B.相交 C.相离 D.平行
3.平面内,☉O的半径为5,若直线l与☉O相离,则圆心O到直线l的距离可能是 ( )
A.6 B.5 C.4 D.3
4.(2024·三明二模)如图,在△ABC中,AB=AC,边BC与☉A相切于点D,边AB,AC与☉A分别交于点M,N.求证:=.
真题精粹·重变式
1.(2024·福建)如图,已知点A,B在☉O上,∠AOB=72°,直线MN与☉O相切,切点为C,且C为的中点,则∠ACM等于 ( )
A.18°
B.30°
C.36°
D.72°
2.(2021·福建)如图,AB为☉O的直径,点P在AB的延长线上,PC,PD与☉O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于 ( )
A. B. C. D.
3.(2019·福建)如图,PA,PB是☉O的切线,A,B为切点,点C在☉O上,且∠ACB=55°,则∠APB等于 ( )
A.55°
B.70°
C.110°
D.125°
4.(2023·福建)如图,已知△ABC内接于☉O,CO的延长线交AB于点D,交☉O于点E,交☉O的切线AF于点F,且AF∥BC.
(1)求证:AO∥BE.
(2)求证:AO平分∠BAC.
5.(2020·福建)如图,AB与☉O相切于点B,AO交☉O于点C,AO的延长线交☉O于点D,E是上不与点B,D重合的点,sin A=.
(1)求∠BED的度数.
(2)若☉O的半径为3,点F在AB的延长线上,且BF=3,求证:DF与☉O相切.
核心突破·拓思维
考点 切线的判定
如图,在△ABC中,CA=CB,O为AB上一点.以O为圆心,OB长为半径的☉O过点C,交AB于另一点D,若D是OA的中点,求证:AC是☉O的切线.
由CA=CB 可得∠A=∠B
可证△AOC≌△BDC ∠ACO=∠BCD=90°
即可得AC是☉O的切线
核心方法
证明直线与圆相切常见情形
(1)已知半径,证垂直;(2)已知垂直,证半径;(3)半径、垂直都不知,作垂线试一试.
如图,△ABC内接于☉O,AB是☉O的直径,∠A=60°.点E在AB延长线上,BE=OB.过点E作ED⊥AC,交AC的延长线于点D. 求证:DE是☉O的切线.
如图,△ABC为☉O内接三角形,∠B=2∠A,点M为直径AB上一点,过点M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF 是☉O 的切线.
(2)设☉O 的半径为2,且AC=CE,求AM 的长.
参考答案
回归教材·过基础
基础演练
1.B 2.B 3.A
4.证明:连接AD,如图所示.
∵BC与☉A相切于点D,
∴AD⊥BC.
∵AB=AC,
∴∠BAD=∠CAD,
∴=.
真题精粹·重变式
1.A 2.D 3.B
4.证明:(1)∵AF是☉O的切线,
∴AF⊥OA,即∠OAF=90°.
∵CE是☉O的直径,
∴∠CBE=90°,∴∠OAF=∠CBE.
∵AF∥BC,∴∠BAF=∠ABC,
∴∠OAF-∠BAF=∠CBE-∠ABC,
即∠OAB=∠ABE,
∴AO∥BE.
(2)∵∠ABE与∠ACE都是所对的圆周角,
∴∠ABE=∠ACE.
∵OA=OC,∴∠ACE=∠OAC,
∴∠ABE=∠OAC,
由(1)知∠OAB=∠ABE,
∴∠OAB=∠OAC,
∴AO平分∠BAC.
5.解析:(1)如图1,连接OB.
图1
∵AB与☉O相切于点B,
∴∠ABO=90°.
∵sin A=,
∴∠A=30°,∴∠BOD=∠ABO+∠A=120°,
∴∠BED=∠BOD=60°.
(2)证明:如图2,连接OF,OB.
图2
∵AB是切线,∴∠OBF=90°.
∵BF=3,OB=3,
∴tan∠BOF==,∴∠BOF=60°.
∵∠BOD=120°,
∴∠BOF=∠DOF=60°.
在△BOF和△DOF中,
∴△BOF≌△DOF(SAS),
∴∠OBF=∠ODF=90°,∴DF与☉O相切.
核心突破·拓思维
例 证明:如图,连接OC,CD.
∵CA=CB,
∴∠A=∠B.
∵BD是直径,
∴∠BCD=90°.
∵D是OA的中点,
∴AD=OD.
又OB=OD,∴AO=BD,
∴△AOC≌△BDC(SAS),
∴∠ACO=∠BCD=90°,∴OC⊥AC.
∵C为半径OC的外端点,
∴AC是☉O的切线.
变式1 证明:如图,过点O作OF⊥DE于点F.
∵ED⊥AC,
∴∠D=90°.
又∵∠A=60°,
∴∠E=30°,
∴OF=OE.
∵BE=OB,
∴OB=OE,
∴OF=OB,则点F在☉O上,
∴DE是☉O的切线.
变式2 解析:(1)证明:如图,连接OC.
∵AB是☉O的直径,
∴∠ACB=90°.
又∵∠B=2∠A,
∴∠B=60°,∠A=30°,
∵EM⊥AB,∴∠EMB=90°.
在Rt△EMB中,∠B=60°,∴∠E=30°.
又∵EF=FC,∴∠ECF=∠E=30°.
又∵∠ECA=90°,∴∠FCA=60°.
∵OA=OC,∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,∴FC是☉O的切线.
(2)在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,AC=BC=2.
∵AC=CE,∴CE=2,
∴BE=BC+CE=2+2.
在Rt△BEM中,∠BME=90°,∠E=30°,
∴BM=BE=1+,
∴AM=AB-BM=4-1-=3-.
同课章节目录
