第三章 函数 第1节 平面直角坐标系与函数 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 第三章 函数 第1节 平面直角坐标系与函数 学案(含答案)2025年中考数学人教版一轮复习考点探究 |
|
|
| 格式 | docx | ||
| 文件大小 | 400.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 08:34:55 | ||
图片预览



文档简介
第1节 平面直角坐标系与函数
回归教材·过基础
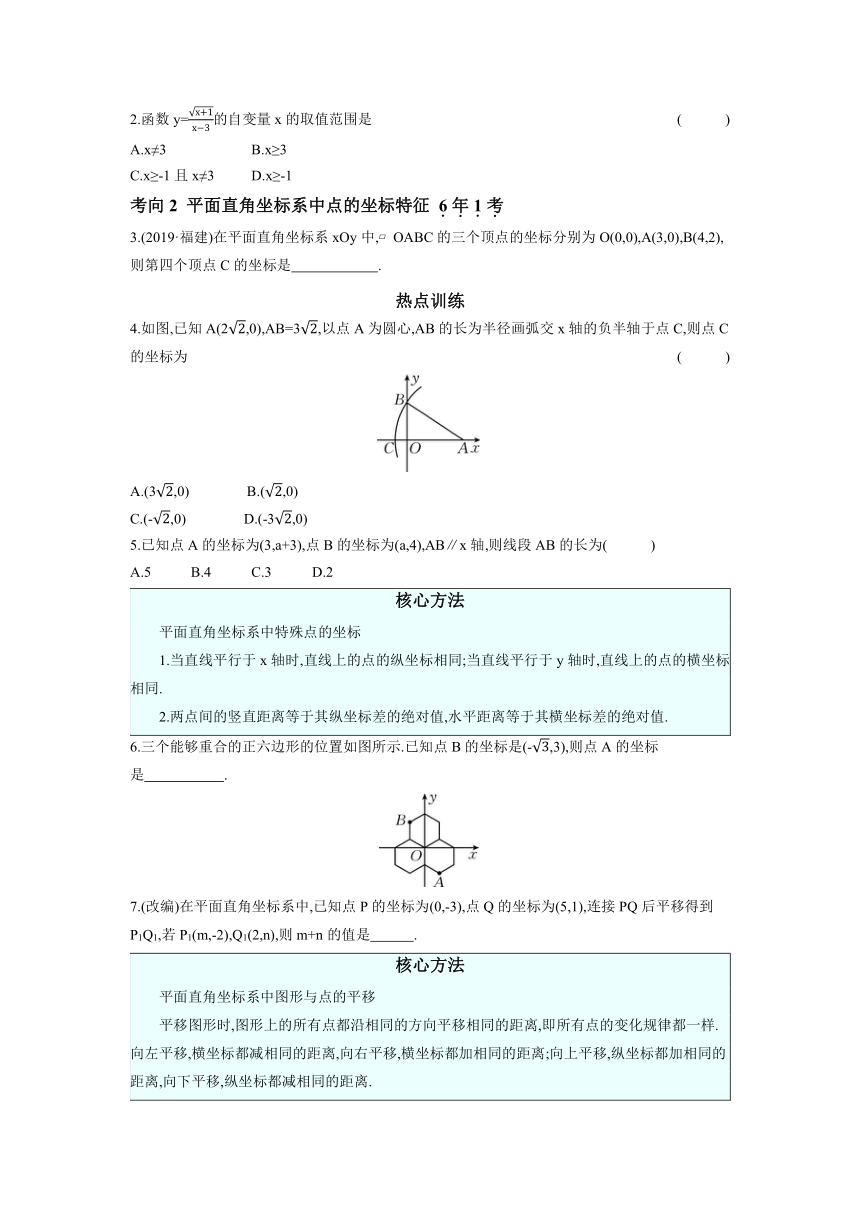
【知识体系】
【考点清单】
知识点1 平面直角坐标系及点的坐标特征
1.点的坐标特征
点在象限内 点在坐标轴上 点在平行于坐标轴的直线上 点在各象限角平分线上
第一象限:x>0,y>0; 第二象限:x① 0, y② 0; 第三象限:x③ 0, y④ 0; 第四象限:x⑤ 0, y⑥ 0 当点在x轴上时, 该点的⑦ 等于0;当点在y轴上时, 该点的⑧ 等于0 平行于x轴的直线上的点,所有点 的⑨ 都相等; 平行于y轴的直线上的点,所有点 的⑩ 都相等 第一、三象限角平分线上的点:xA=yA; 第二、四象限角平分线上的点:
2.点的对称与平移
(1)对称
(2)平移
3.点到坐标轴及原点的距离
点到x轴的距离是|y| 点到y轴的距离是 点到原点的距离是
4.平面内两点之间的距离
若P,Q两点的连线平行于x轴,则这两点之间的距离是|PQ|=|x1-x2| 若P,Q两点的连线平行于y轴,则这两点之间的距离是|PQ|= 平面内任意P,Q两点之间的距离是|PQ|=
知识点2 函数及自变量的取值范围
1.概念:在某个变化过程中有两个变量x,y,如果对于x的每一个确定的值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
2.不同函数中自变量x的取值范围
3.函数的表示方法:解析式法、列表法、图象法.
4.函数的图象的画法:列表、描点、连线.
真题精粹·重变式
考向1 函数自变量的取值范围
热点训练 1.函数y=中,自变量x的取值范围是 ( ) A.x≤-2 B.x≥-2 C.x≤2 D.x≥2
2.函数y=的自变量x的取值范围是 ( ) A.x≠3 B.x≥3 C.x≥-1且x≠3 D.x≥-1
考向2 平面直角坐标系中点的坐标特征 6年1考
3.(2019·福建)在平面直角坐标系xOy中, OABC的三个顶点的坐标分别为O(0,0),A(3,0),B(4,2),则第四个顶点C的坐标是 .
热点训练 4.如图,已知A(2,0),AB=3,以点A为圆心,AB的长为半径画弧交x轴的负半轴于点C,则点C的坐标为 ( ) A.(3,0) B.(,0) C.(-,0) D.(-3,0) 5.已知点A的坐标为(3,a+3),点B的坐标为(a,4),AB∥x轴,则线段AB的长为( ) A.5 B.4 C.3 D.2 核心方法 平面直角坐标系中特殊点的坐标 1.当直线平行于x轴时,直线上的点的纵坐标相同;当直线平行于y轴时,直线上的点的横坐标相同. 2.两点间的竖直距离等于其纵坐标差的绝对值,水平距离等于其横坐标差的绝对值. 6.三个能够重合的正六边形的位置如图所示.已知点B的坐标是(-,3),则点A的坐标是 . 7.(改编)在平面直角坐标系中,已知点P的坐标为(0,-3),点Q的坐标为(5,1),连接PQ后平移得到P1Q1,若P1(m,-2),Q1(2,n),则m+n的值是 . 核心方法 平面直角坐标系中图形与点的平移 平移图形时,图形上的所有点都沿相同的方向平移相同的距离,即所有点的变化规律都一样.向左平移,横坐标都减相同的距离,向右平移,横坐标都加相同的距离;向上平移,纵坐标都加相同的距离,向下平移,纵坐标都减相同的距离.
考向3 函数图象的分析与判断
热点训练 8.根据数学家凯勒的“百米赛跑数学模型”,前30m称为“加速期”,30m~80m为“中途期”,80m~100m为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(单位:m/s)与路程x(单位:m)之间的观测数据绘制成曲线,如图所示. (1)y是关于x的函数吗 为什么 (2)“加速期”结束时,小斌的速度为多少 (3)根据图中提供的信息,给小斌提一条训练建议.
9.通过课本上对函数的学习,我们积累了一定的经验.下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题: x…012345…y…6321.51.21…
(1)当x= 时,y=1.5. (2)根据表中数值描点(x,y),并在如图的平面直角坐标系画出函数图象.
(3)观察画出的图象,写出这个函数的一条性质: .
核心突破·拓思维
考点1 平面直角坐标系中点的特征
(原创)如图1,正方形ABCD的边长为3个单位长度,点A的坐标为(1,2),边AB,CD都平行于x轴,与y轴分别相交于点E,G,边AD,BC都平行于y轴,与x轴分别相交于点H,F.
(1)点B,C,D,E,F的坐标分别为 .
(2)AE= ,BE= ,BF= ,CF= .
(3)将正方形ABCD沿x轴向右平移0.5个单位长度,向下平移0.5个单位长度.
①请在图2的网格中画出平移后的正方形A1B1C1D1,并写出点A,B,C,D的对应点A1,B1,C1,D1的坐标.
②点A1与点C1的位置关系为 ,点A1与点B1的位置关系为 ,点A1与点D1的位置关系为 .
③点B1到x轴的距离为 ,到y轴的距离为 .
核心方法
平移图形时,图形上所有点的变化规律都一样.
一般规律为向左(右)平移几个单位长度,横坐标都减(加)相同的单位长度;向上(下)平移几个单位长度,纵坐标都加(减)相同的单位长度.
如图,这是一片枫叶标本,其形状呈“掌状五裂形”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”的A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 .
在平面直角坐标系xOy中,正方形ABCD的顶点A,B的坐标分别为(m,m),(m,m-5),则点C的坐标为 .(用含m的式子表示)
数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”.据传,他在计算1+2+3+4+…+100时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+…+100=.人们借助这样的方法,得到1+2+3+4+…+n=(n是正整数).如图,在平面直角坐标系中的一系列格点Ai(xi,yi),其中i=1,2,3,…,n,…,且xi,yi均为整数.记an=xn+yn,如A1(0,0),即a1=0,A2(1,0),即a2=1,A3(1,-1),即a3=0,…,以此类推.
则下列结论正确的是 ( )
A.a2 023=40
B.a2 024=43
C.=2n-6
D.=2n-4
考点2 函数图象的分析与判断
如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为 ( )
A B
C D
【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游览路线①④⑤⑥⑦⑧用时3小时25分钟;小州游览路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为 ( )
A.4 200米 B.4 800米
C.5 200米 D.5 400米
参考答案
回归教材·过基础
考点清单
①< ②> ③< ④< ⑤> ⑥< ⑦纵坐标
⑧横坐标 ⑨纵坐标 ⑩横坐标 xB=-yB
(-x, y) (-x,-y) (x+a,y) (x,y+b)
(x,y-b) |x| |y1-y2|
真题精粹·重变式
1.D 2.C 3.(1,2) 4.C 5.D 6.(,-3) 7.-1
8.解析:(1)y是关于x的函数.在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80 m左右时速度下降明显,建议增加耐力训练,提高成绩.
9.解析:(1)3.
(2)函数图象如图所示:
(3)函数值y随x的增大而减小(答案不唯一).
核心突破·拓思维
例1 解析:(1)(-2,2),(-2,-1),(1,-1),(0,2),(-2,0) (2)1 2 2 1
(3)①画出的正方形A1B1C1D1如图所示.
A1,,B1-,,
C1-,-,D1,-.
②关于原点O对称 关于y轴对称 关于x轴对称
③
变式1 (2,-3)
变式2 (m+5,m-5)或(m-5,m-5)
变式3 B
例2 C
变式 B
回归教材·过基础
【知识体系】
【考点清单】
知识点1 平面直角坐标系及点的坐标特征
1.点的坐标特征
点在象限内 点在坐标轴上 点在平行于坐标轴的直线上 点在各象限角平分线上
第一象限:x>0,y>0; 第二象限:x① 0, y② 0; 第三象限:x③ 0, y④ 0; 第四象限:x⑤ 0, y⑥ 0 当点在x轴上时, 该点的⑦ 等于0;当点在y轴上时, 该点的⑧ 等于0 平行于x轴的直线上的点,所有点 的⑨ 都相等; 平行于y轴的直线上的点,所有点 的⑩ 都相等 第一、三象限角平分线上的点:xA=yA; 第二、四象限角平分线上的点:
2.点的对称与平移
(1)对称
(2)平移
3.点到坐标轴及原点的距离
点到x轴的距离是|y| 点到y轴的距离是 点到原点的距离是
4.平面内两点之间的距离
若P,Q两点的连线平行于x轴,则这两点之间的距离是|PQ|=|x1-x2| 若P,Q两点的连线平行于y轴,则这两点之间的距离是|PQ|= 平面内任意P,Q两点之间的距离是|PQ|=
知识点2 函数及自变量的取值范围
1.概念:在某个变化过程中有两个变量x,y,如果对于x的每一个确定的值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
2.不同函数中自变量x的取值范围
3.函数的表示方法:解析式法、列表法、图象法.
4.函数的图象的画法:列表、描点、连线.
真题精粹·重变式
考向1 函数自变量的取值范围
热点训练 1.函数y=中,自变量x的取值范围是 ( ) A.x≤-2 B.x≥-2 C.x≤2 D.x≥2
2.函数y=的自变量x的取值范围是 ( ) A.x≠3 B.x≥3 C.x≥-1且x≠3 D.x≥-1
考向2 平面直角坐标系中点的坐标特征 6年1考
3.(2019·福建)在平面直角坐标系xOy中, OABC的三个顶点的坐标分别为O(0,0),A(3,0),B(4,2),则第四个顶点C的坐标是 .
热点训练 4.如图,已知A(2,0),AB=3,以点A为圆心,AB的长为半径画弧交x轴的负半轴于点C,则点C的坐标为 ( ) A.(3,0) B.(,0) C.(-,0) D.(-3,0) 5.已知点A的坐标为(3,a+3),点B的坐标为(a,4),AB∥x轴,则线段AB的长为( ) A.5 B.4 C.3 D.2 核心方法 平面直角坐标系中特殊点的坐标 1.当直线平行于x轴时,直线上的点的纵坐标相同;当直线平行于y轴时,直线上的点的横坐标相同. 2.两点间的竖直距离等于其纵坐标差的绝对值,水平距离等于其横坐标差的绝对值. 6.三个能够重合的正六边形的位置如图所示.已知点B的坐标是(-,3),则点A的坐标是 . 7.(改编)在平面直角坐标系中,已知点P的坐标为(0,-3),点Q的坐标为(5,1),连接PQ后平移得到P1Q1,若P1(m,-2),Q1(2,n),则m+n的值是 . 核心方法 平面直角坐标系中图形与点的平移 平移图形时,图形上的所有点都沿相同的方向平移相同的距离,即所有点的变化规律都一样.向左平移,横坐标都减相同的距离,向右平移,横坐标都加相同的距离;向上平移,纵坐标都加相同的距离,向下平移,纵坐标都减相同的距离.
考向3 函数图象的分析与判断
热点训练 8.根据数学家凯勒的“百米赛跑数学模型”,前30m称为“加速期”,30m~80m为“中途期”,80m~100m为“冲刺期”.市田径队把运动员小斌某次百米跑训练时速度y(单位:m/s)与路程x(单位:m)之间的观测数据绘制成曲线,如图所示. (1)y是关于x的函数吗 为什么 (2)“加速期”结束时,小斌的速度为多少 (3)根据图中提供的信息,给小斌提一条训练建议.
9.通过课本上对函数的学习,我们积累了一定的经验.下表是一个函数的自变量x与函数值y的部分对应值,请你借鉴以往学习函数的经验,探究下列问题: x…012345…y…6321.51.21…
(1)当x= 时,y=1.5. (2)根据表中数值描点(x,y),并在如图的平面直角坐标系画出函数图象.
(3)观察画出的图象,写出这个函数的一条性质: .
核心突破·拓思维
考点1 平面直角坐标系中点的特征
(原创)如图1,正方形ABCD的边长为3个单位长度,点A的坐标为(1,2),边AB,CD都平行于x轴,与y轴分别相交于点E,G,边AD,BC都平行于y轴,与x轴分别相交于点H,F.
(1)点B,C,D,E,F的坐标分别为 .
(2)AE= ,BE= ,BF= ,CF= .
(3)将正方形ABCD沿x轴向右平移0.5个单位长度,向下平移0.5个单位长度.
①请在图2的网格中画出平移后的正方形A1B1C1D1,并写出点A,B,C,D的对应点A1,B1,C1,D1的坐标.
②点A1与点C1的位置关系为 ,点A1与点B1的位置关系为 ,点A1与点D1的位置关系为 .
③点B1到x轴的距离为 ,到y轴的距离为 .
核心方法
平移图形时,图形上所有点的变化规律都一样.
一般规律为向左(右)平移几个单位长度,横坐标都减(加)相同的单位长度;向上(下)平移几个单位长度,纵坐标都加(减)相同的单位长度.
如图,这是一片枫叶标本,其形状呈“掌状五裂形”,裂片具有少数突出的齿,将其放在平面直角坐标系中,表示叶片“顶部”的A,B两点的坐标分别为(-2,2),(-3,0),则叶杆“底部”点C的坐标为 .
在平面直角坐标系xOy中,正方形ABCD的顶点A,B的坐标分别为(m,m),(m,m-5),则点C的坐标为 .(用含m的式子表示)
数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”.据传,他在计算1+2+3+4+…+100时,用到了一种方法,将首尾两个数相加,进而得到1+2+3+4+…+100=.人们借助这样的方法,得到1+2+3+4+…+n=(n是正整数).如图,在平面直角坐标系中的一系列格点Ai(xi,yi),其中i=1,2,3,…,n,…,且xi,yi均为整数.记an=xn+yn,如A1(0,0),即a1=0,A2(1,0),即a2=1,A3(1,-1),即a3=0,…,以此类推.
则下列结论正确的是 ( )
A.a2 023=40
B.a2 024=43
C.=2n-6
D.=2n-4
考点2 函数图象的分析与判断
如图,长方体水池内有一无盖圆柱形铁桶,现用水管往铁桶中持续匀速注水,直到长方体水池有水溢出一会儿为止.设注水时间为t,y1(细实线)表示铁桶中水面高度,y2(粗实线)表示水池中水面高度(铁桶高度低于水池高度,铁桶底面积小于水池底面积的一半,注水前铁桶和水池内均无水),则y1,y2随时间t变化的函数图象大致为 ( )
A B
C D
【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游览路线①④⑤⑥⑦⑧用时3小时25分钟;小州游览路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为 ( )
A.4 200米 B.4 800米
C.5 200米 D.5 400米
参考答案
回归教材·过基础
考点清单
①< ②> ③< ④< ⑤> ⑥< ⑦纵坐标
⑧横坐标 ⑨纵坐标 ⑩横坐标 xB=-yB
(-x, y) (-x,-y) (x+a,y) (x,y+b)
(x,y-b) |x| |y1-y2|
真题精粹·重变式
1.D 2.C 3.(1,2) 4.C 5.D 6.(,-3) 7.-1
8.解析:(1)y是关于x的函数.在这个变化过程中,对于x的每一个确定的值,y都有唯一确定的值与之对应.
(2)“加速期”结束时,小斌的速度为10.4m/s.
(3)答案不唯一.例如:根据图象信息,小斌在80 m左右时速度下降明显,建议增加耐力训练,提高成绩.
9.解析:(1)3.
(2)函数图象如图所示:
(3)函数值y随x的增大而减小(答案不唯一).
核心突破·拓思维
例1 解析:(1)(-2,2),(-2,-1),(1,-1),(0,2),(-2,0) (2)1 2 2 1
(3)①画出的正方形A1B1C1D1如图所示.
A1,,B1-,,
C1-,-,D1,-.
②关于原点O对称 关于y轴对称 关于x轴对称
③
变式1 (2,-3)
变式2 (m+5,m-5)或(m-5,m-5)
变式3 B
例2 C
变式 B
同课章节目录
