第四章 三角形 第5节 直角三角形与勾股定理 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 第四章 三角形 第5节 直角三角形与勾股定理 学案(含答案)2025年中考数学人教版一轮复习考点探究 |  | |
| 格式 | docx | ||
| 文件大小 | 89.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 08:47:20 | ||
图片预览


文档简介
第5节 直角三角形与勾股定理
回归教材·过基础
【考点清单】
知识点1 直角三角形的性质与判定
直角 三角形 性质 直角三角形的两个锐角①
直角三角形中斜边上的中线等于②
判定 有一个角为③ 的三角形是直角三角形
有两个角④ 的三角形是直角三角形
如果三角形的一边上的中线等于这条边的一半,那么这个三角形是直角三角形
含30°角的 直角三角形的性质 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于⑤
30°角的判定 若一条直角边等于斜边的一半,则这条直角边所对的锐角等于30°
拓展 (1)SRt△ABC=ch=ab,其中a,b为两直角边,c为斜边,h为斜边上的高; (2)Rt△ABC内切圆的半径r=,外接圆的半径R=,即斜边的一半
知识点2 勾股定理及其逆定理
1.勾股定理
(1)如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么⑥ .
(2)能构成直角三角形的三条边长的三个正整数,称为勾股数.
2.勾股定理的逆定理
如果三角形的三边长分别为a,c,b,且满足⑦ ,那么这个三角形是直角三角形.
技巧提示
运用勾股定理时,应分清直角边和斜边,斜边为最长边,即斜边的平方等于两直角边的平方和.
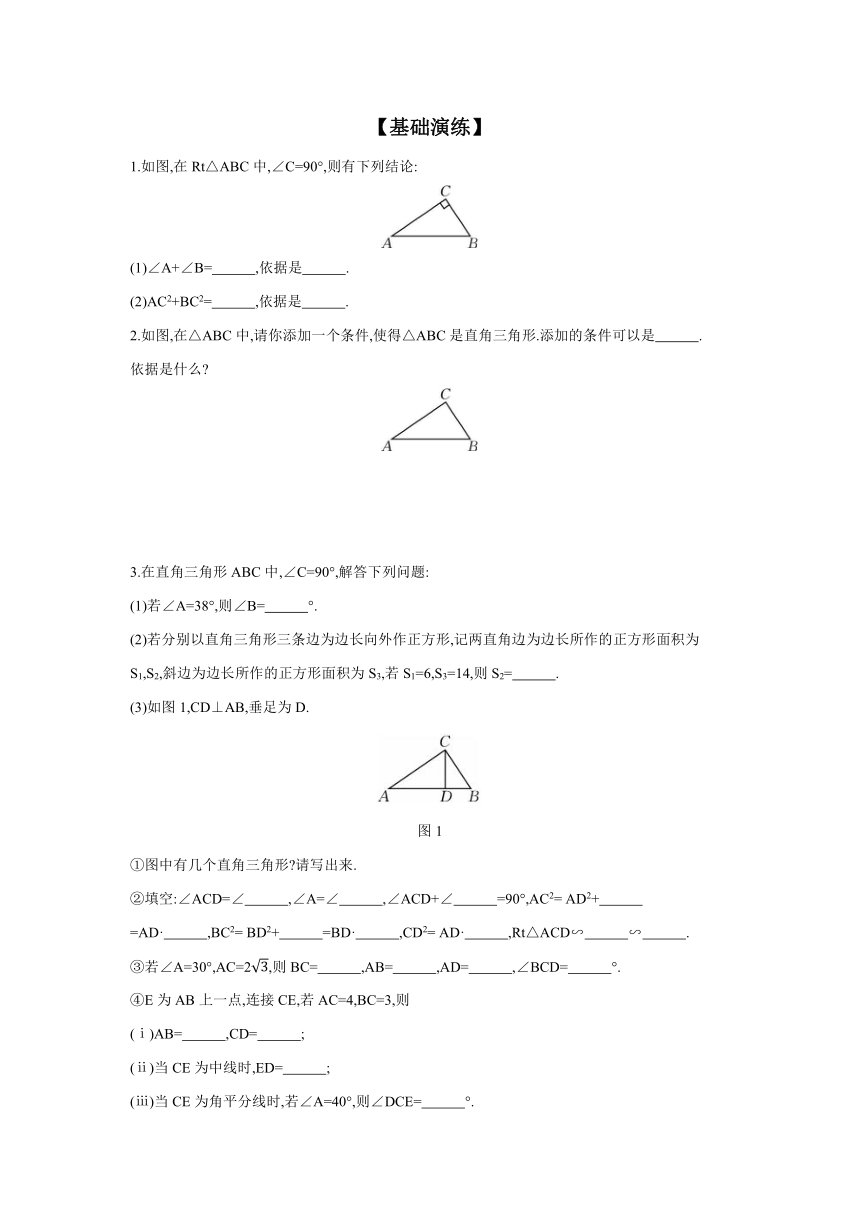
【基础演练】
1.如图,在Rt△ABC中,∠C=90°,则有下列结论:
(1)∠A+∠B= ,依据是 .
(2)AC2+BC2= ,依据是 .
2.如图,在△ABC中,请你添加一个条件,使得△ABC是直角三角形.添加的条件可以是 .
依据是什么
3.在直角三角形ABC中,∠C=90°,解答下列问题:
(1)若∠A=38°,则∠B= °.
(2)若分别以直角三角形三条边为边长向外作正方形,记两直角边为边长所作的正方形面积为S1,S2,斜边为边长所作的正方形面积为S3,若S1=6,S3=14,则S2= .
(3)如图1,CD⊥AB,垂足为D.
图1
①图中有几个直角三角形 请写出来.
②填空:∠ACD=∠ ,∠A=∠ ,∠ACD+∠ =90°,AC2= AD2+ =AD· ,BC2= BD2+ =BD· ,CD2= AD· ,Rt△ACD∽ ∽ .
③若∠A=30°,AC=2,则BC= ,AB= ,AD= ,∠BCD= °.
④E为AB上一点,连接CE,若AC=4,BC=3,则
(ⅰ)AB= ,CD= ;
(ⅱ)当CE为中线时,ED= ;
(ⅲ)当CE为角平分线时,若∠A=40°,则∠DCE= °.
(4)如图2、图3,∠ACB=90°,直线l经过点C,过点A,B分别作BD⊥l,AE⊥l,垂足分别为D,E,若AC=BC,则所得的△ACE和△CBD有什么关系 试猜想DE,BD,AE之间的数量关系,并证明你的结论.
图2 图3
4.如图,以AB所在的直线为x轴,过点C的直线为y轴,建立平面直角坐标系xOy,若OA=4,OB=1,OC=2.
(1)写出点A,B,C的坐标,并求直线BC的解析式.
(2)若点D在y轴上,将BC沿直线BD对折,使BC正好落在x轴上,点C的对应点为C',求点D的坐标.
真题精粹·重变式
考向1 直角三角形的性质与判定
1.(2021·福建)如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于 ( )
A.2 km B.3 km
C.2 km D.4 km
热点训练 2.如图,在Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .
考向2 勾股定理及其逆定理
热点训练 3.把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB=,则CD= . 核心方法 利用直角三角形求线段长的方法 1.勾股定理是揭示直角三角形三边关系的定理.若已知直角三角形中的两边长,则可求出第三边长;若已知直角三角形三边的关系,则可设未知边长,根据勾股定理列方程求解. 2.在直角三角形中求边长,首先要考虑的是用勾股定理求解.当直角三角形中出现30°角时应联想到30°角所对的直角边是斜边的一半,当出现斜边上的中线时要想到直角三角形中斜边上的中线等于斜边的一半,这些线段间的数量关系是直角三角形中求线段长的关键. 3.若图形中含折叠,则考虑用折叠的性质,然后在直角三角形中,设未知量,列方程求解. 4.若所求为线段和(或可转化为线段和的形式),考虑用证全等转化到直角三角形中求解.
4.以2,3为直角边的直角三角形的斜边长为 ( ) A. B. C.4 D.5 5.如图,已知正方形A的面积为3,正方形B的面积为4,则正方形C的面积为 . 6.(数学文化)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是25,小正方形的面积是1,则AE= . 7.《九章算术》勾股章有一问题,其意思:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长 若设绳索长度为x尺,根据题意,可列方程: .
参考答案
回归教材·过基础
考点清单
①互余 ②斜边的一半 ③90° ④互余 ⑤斜边的一半
⑥c2=a2+b2 ⑦a2+b2=c2
基础演练
1.(1)90° 直角三角形两个锐角互为余角
(2)AB2 直角三角形两直角边的平方和等于斜边的平方
2.解析:(1)∠A+∠B=90°或∠C=90°,依据是两个锐角互为余角的三角形是直角三角形,或者有一个角是直角的三角形是直角三角形.
(2)AC2+BC2=AB2 ,依据是在三角形中,如果两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
3.解析:(1)52 (2)8
(3)①三个直角三角形,分别是Rt△ACD,Rt△BCD,Rt△ABC.
②B BCD A(或BCD) CD2 AB CD2 AB BD Rt△CBD Rt△ABC ③2 4 3 30 ④5 5
(4)解析:△ACE≌△CBD,DE=BD+AE(另一种情况自行证明).
证明:∵∠ACB=90°,BD⊥l,AE⊥l,
∴∠AEC=∠CDB=∠ACB=90°,
∴∠EAC+∠ECA=∠BCD+∠ECA=90°,
∴∠EAC=∠BCD.
∵在△ACE和△CBD中,∠EAC=∠DCB,∠AEC=∠CDB,AC=CB,
∴△ACE≌△CBD(AAS),
∴CE=BD,AE=CD,
∴CE +CD=BD+AE,
∴DE=BD+AE.
4.解析:(1)A(-4,0), B(1,0),C(0,2).
设直线BC的解析式为y=kx+b,
依题意得解得
∴y=-2x+2.
(2)①如图1,当点D在y轴的正半轴上时,可得BC'=BC,
图1
根据勾股定理,得BC==,∴OC'=BC'-OB=-1,DC'=DC=OC-OD=2-OD.
在Rt△DC'O中,∵OD2+C'O2=C'D2,
∴OD2+(-1)2=(2-OD)2,
解得OD=,∴点D的坐标为0,.
②如图2,当点D在y轴的负半轴上时,可得BC'=BC,DC'=DC,
图2
根据勾股定理,得BC==,∴OC'=BC'+OB=+1,DC'=DC=OD+OC=OD+2.
在Rt△DC'O中,∵OD2+C'O2=C'D2,
∴OD2+(+1)2=(2+OD)2,
解得OD=,∴点D的坐标为0,-.
综上所述,点D的坐标为0,或0,-.
真题精粹·重变式
1.D 2.3 3.-1 4.B 5.7 6.3
7.(x-3)2+82=x2
回归教材·过基础
【考点清单】
知识点1 直角三角形的性质与判定
直角 三角形 性质 直角三角形的两个锐角①
直角三角形中斜边上的中线等于②
判定 有一个角为③ 的三角形是直角三角形
有两个角④ 的三角形是直角三角形
如果三角形的一边上的中线等于这条边的一半,那么这个三角形是直角三角形
含30°角的 直角三角形的性质 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于⑤
30°角的判定 若一条直角边等于斜边的一半,则这条直角边所对的锐角等于30°
拓展 (1)SRt△ABC=ch=ab,其中a,b为两直角边,c为斜边,h为斜边上的高; (2)Rt△ABC内切圆的半径r=,外接圆的半径R=,即斜边的一半
知识点2 勾股定理及其逆定理
1.勾股定理
(1)如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么⑥ .
(2)能构成直角三角形的三条边长的三个正整数,称为勾股数.
2.勾股定理的逆定理
如果三角形的三边长分别为a,c,b,且满足⑦ ,那么这个三角形是直角三角形.
技巧提示
运用勾股定理时,应分清直角边和斜边,斜边为最长边,即斜边的平方等于两直角边的平方和.
【基础演练】
1.如图,在Rt△ABC中,∠C=90°,则有下列结论:
(1)∠A+∠B= ,依据是 .
(2)AC2+BC2= ,依据是 .
2.如图,在△ABC中,请你添加一个条件,使得△ABC是直角三角形.添加的条件可以是 .
依据是什么
3.在直角三角形ABC中,∠C=90°,解答下列问题:
(1)若∠A=38°,则∠B= °.
(2)若分别以直角三角形三条边为边长向外作正方形,记两直角边为边长所作的正方形面积为S1,S2,斜边为边长所作的正方形面积为S3,若S1=6,S3=14,则S2= .
(3)如图1,CD⊥AB,垂足为D.
图1
①图中有几个直角三角形 请写出来.
②填空:∠ACD=∠ ,∠A=∠ ,∠ACD+∠ =90°,AC2= AD2+ =AD· ,BC2= BD2+ =BD· ,CD2= AD· ,Rt△ACD∽ ∽ .
③若∠A=30°,AC=2,则BC= ,AB= ,AD= ,∠BCD= °.
④E为AB上一点,连接CE,若AC=4,BC=3,则
(ⅰ)AB= ,CD= ;
(ⅱ)当CE为中线时,ED= ;
(ⅲ)当CE为角平分线时,若∠A=40°,则∠DCE= °.
(4)如图2、图3,∠ACB=90°,直线l经过点C,过点A,B分别作BD⊥l,AE⊥l,垂足分别为D,E,若AC=BC,则所得的△ACE和△CBD有什么关系 试猜想DE,BD,AE之间的数量关系,并证明你的结论.
图2 图3
4.如图,以AB所在的直线为x轴,过点C的直线为y轴,建立平面直角坐标系xOy,若OA=4,OB=1,OC=2.
(1)写出点A,B,C的坐标,并求直线BC的解析式.
(2)若点D在y轴上,将BC沿直线BD对折,使BC正好落在x轴上,点C的对应点为C',求点D的坐标.
真题精粹·重变式
考向1 直角三角形的性质与判定
1.(2021·福建)如图,某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2 km.据此,可求得学校与工厂之间的距离AB等于 ( )
A.2 km B.3 km
C.2 km D.4 km
热点训练 2.如图,在Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD= .
考向2 勾股定理及其逆定理
热点训练 3.把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB=,则CD= . 核心方法 利用直角三角形求线段长的方法 1.勾股定理是揭示直角三角形三边关系的定理.若已知直角三角形中的两边长,则可求出第三边长;若已知直角三角形三边的关系,则可设未知边长,根据勾股定理列方程求解. 2.在直角三角形中求边长,首先要考虑的是用勾股定理求解.当直角三角形中出现30°角时应联想到30°角所对的直角边是斜边的一半,当出现斜边上的中线时要想到直角三角形中斜边上的中线等于斜边的一半,这些线段间的数量关系是直角三角形中求线段长的关键. 3.若图形中含折叠,则考虑用折叠的性质,然后在直角三角形中,设未知量,列方程求解. 4.若所求为线段和(或可转化为线段和的形式),考虑用证全等转化到直角三角形中求解.
4.以2,3为直角边的直角三角形的斜边长为 ( ) A. B. C.4 D.5 5.如图,已知正方形A的面积为3,正方形B的面积为4,则正方形C的面积为 . 6.(数学文化)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是25,小正方形的面积是1,则AE= . 7.《九章算术》勾股章有一问题,其意思:现有一竖立着的木柱,在木柱上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有3尺,牵着绳索退行,在离木柱根部8尺处时绳索用尽,请问绳索有多长 若设绳索长度为x尺,根据题意,可列方程: .
参考答案
回归教材·过基础
考点清单
①互余 ②斜边的一半 ③90° ④互余 ⑤斜边的一半
⑥c2=a2+b2 ⑦a2+b2=c2
基础演练
1.(1)90° 直角三角形两个锐角互为余角
(2)AB2 直角三角形两直角边的平方和等于斜边的平方
2.解析:(1)∠A+∠B=90°或∠C=90°,依据是两个锐角互为余角的三角形是直角三角形,或者有一个角是直角的三角形是直角三角形.
(2)AC2+BC2=AB2 ,依据是在三角形中,如果两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
3.解析:(1)52 (2)8
(3)①三个直角三角形,分别是Rt△ACD,Rt△BCD,Rt△ABC.
②B BCD A(或BCD) CD2 AB CD2 AB BD Rt△CBD Rt△ABC ③2 4 3 30 ④5 5
(4)解析:△ACE≌△CBD,DE=BD+AE(另一种情况自行证明).
证明:∵∠ACB=90°,BD⊥l,AE⊥l,
∴∠AEC=∠CDB=∠ACB=90°,
∴∠EAC+∠ECA=∠BCD+∠ECA=90°,
∴∠EAC=∠BCD.
∵在△ACE和△CBD中,∠EAC=∠DCB,∠AEC=∠CDB,AC=CB,
∴△ACE≌△CBD(AAS),
∴CE=BD,AE=CD,
∴CE +CD=BD+AE,
∴DE=BD+AE.
4.解析:(1)A(-4,0), B(1,0),C(0,2).
设直线BC的解析式为y=kx+b,
依题意得解得
∴y=-2x+2.
(2)①如图1,当点D在y轴的正半轴上时,可得BC'=BC,
图1
根据勾股定理,得BC==,∴OC'=BC'-OB=-1,DC'=DC=OC-OD=2-OD.
在Rt△DC'O中,∵OD2+C'O2=C'D2,
∴OD2+(-1)2=(2-OD)2,
解得OD=,∴点D的坐标为0,.
②如图2,当点D在y轴的负半轴上时,可得BC'=BC,DC'=DC,
图2
根据勾股定理,得BC==,∴OC'=BC'+OB=+1,DC'=DC=OD+OC=OD+2.
在Rt△DC'O中,∵OD2+C'O2=C'D2,
∴OD2+(+1)2=(2+OD)2,
解得OD=,∴点D的坐标为0,-.
综上所述,点D的坐标为0,或0,-.
真题精粹·重变式
1.D 2.3 3.-1 4.B 5.7 6.3
7.(x-3)2+82=x2
同课章节目录
