第五章 四边形 章节构建二 特殊四边形的性质及判定 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 第五章 四边形 章节构建二 特殊四边形的性质及判定 学案(含答案)2025年中考数学人教版一轮复习考点探究 |
|
|
| 格式 | docx | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览





文档简介
章节构建二 特殊四边形的性质及判定
回归教材·过基础
【考点清单】
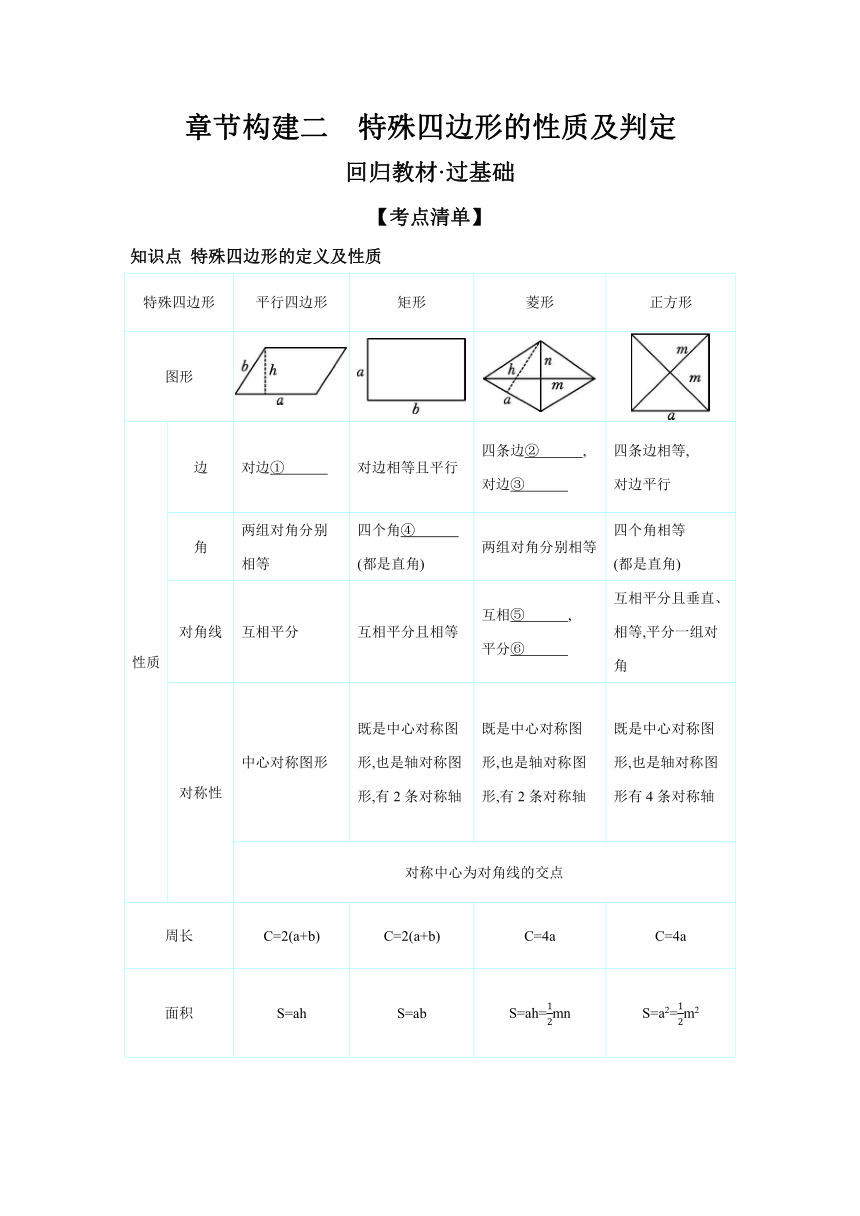
知识点 特殊四边形的定义及性质
特殊四边形 平行四边形 矩形 菱形 正方形
图形
性质 边 对边① 对边相等且平行 四条边② , 对边③ 四条边相等, 对边平行
角 两组对角分别相等 四个角④ (都是直角) 两组对角分别相等 四个角相等 (都是直角)
对角线 互相平分 互相平分且相等 互相⑤ , 平分⑥ 互相平分且垂直、相等,平分一组对角
对称性 中心对称图形 既是中心对称图形,也是轴对称图形,有2条对称轴 既是中心对称图形,也是轴对称图形,有2条对称轴 既是中心对称图形,也是轴对称图形有4条对称轴
对称中心为对角线的交点
周长 C=2(a+b) C=2(a+b) C=4a C=4a
面积 S=ah S=ab S=ah=mn S=a2=m2
【基础演练】
1.矩形的性质与判定:
(1)如图1,在 ABCD中,AC,BD相交于点O,请添加一个条件 (写出一个即可),
使四边形ABCD是矩形.
(2)在(1)的结论下,
①若∠BAC=30°,则∠AOD= ;
②若∠ADO=60°,BD=8,则OA的长为 ,矩形ABCD的面积为 ;
③过点O作OE∥DC交BC于点E,若OE=8,BE=6,则AC的长为 ,
矩形ABCD的周长为 .
(3)如图2,在矩形ABCD中,AB=3,AD=4,对角线AC,BD相交于点O,M,N分别是OC,BC的中点,连接ON,MN,则△OMN的周长为 .
2.菱形的性质与判定:
(1)如图1,在 ABCD中,AC,BD相交于点O,请添加一个条件 (写出一个即可),
使四边形ABCD是菱形.
(2)在(1)的结论下,完成下列问题:
①若AC=12,BD=16,则AO= ,BO= ,AB= ,AD= ;
②若∠ABC=60°,AB=4,则∠BAD= ,∠BAC= ,∠ABD= ,
AC的长是 ,BD的长是 ,四边形ABCD的面积是 ,
四边形ABCD的周长是 ;
③若tan∠BAC=,AC=12,则BD的长是 ;
④若AB=10,E是CD的中点,连接OE,则OE的长是 ;
⑤过点O作OF⊥BC于点F,若AC=12,BD=16,则OF的长是 .
(3)如图2,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AH⊥BC于点H,
若cos∠ABC=,CH=4,则AH的长是 ,AC的长是 ,菱形ABCD的面积为 .
3.正方形的性质与判定:
如图1,已知在正方形ABCD中,对角线AC,BD相交于点O.
(1)∠ABC= ,∠BAC= ,∠AOD= ;
(2)若AD=4,则AB= ,BC= ,AC= ,BD= ,BO= ;
(3)若OC=2,则正方形ABCD的边长是 ,面积是 ,周长是 ;
(4)如图2,在正方形ABCD的外侧作等边△DCE,则∠EAC= .
真题精粹·重变式
考向1 矩形的性质与判定 6年4考
1.(2021·福建)如图,在矩形ABCD中,AB=4,AD=5,E,F分别是边AB,BC上的动点,点E不与点A,B重合,且EF=AB,G是五边形AEFCD内满足GE=GF且∠EGF=90°的点.现给出以下结论:
①∠GEB与∠GFB一定互补;
②点G到边AB,BC的距离一定相等;
③点G到边AD,DC的距离可能相等;
④点G到边AB距离的最大值为2.
其中正确的是 .(写出所有正确结论的序号)
热点训练 2.如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,点B',D'分别是点B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段B'D'的长是 ( ) A. B.2 C. D.1
考向2 菱形的性质与判定 6年1考
3.(2023·福建)如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
热点训练 4.如图,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是 ( ) A.OB=CE B.△ACE是直角三角形 C.BC=AE D.BE=CE
考向3 正方形的性质与判定 6年2考
5.(2024·福建)如图,正方形ABCD的面积为4,E,F,G,H分别为边AB,BC,CD,AD的中点,则四边形EFGH的面积为 .
6.(2021·福建)如图,在正方形ABCD中,E,F为边AB上的两个三等分点,点A关于DE的对称点为点A',AA'的延长线交BC于点G.
(1)求证:DE∥A'F.
(2)求∠GA'B的大小.
(3)求证:A'C=2A'B.
热点训练 7.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D'.若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是 ( ) A.1 B. C. D.
核心突破·拓思维
考点1 矩形的性质和判定
如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,M为AB的中点,连接CM.
(1)求证:四边形ADEC是矩形.
(2)若CM=5,AC=8,求四边形ADEB的面积.
如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=6,AD=ED=10,则BF的长为 ( )
A. B.2 C. D.2
如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,P是AD上不与点A,D重合的一个动点,过点P分别作AC和BD边上的垂线,垂足分别为E,F,则PE+PF的值为 ( )
A. B. C. D.
已知菱形ABCD的对角线AC,BD交于点O,CE∥OD,DE∥OC.求证:四边形OCED是矩形.
如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证: DF=CF.
(2)若∠CDF=60°,DF=6,求矩形ABCD的面积.
考点2 菱形的性质和判定
如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
(1)求证:
①△ADE≌△CDF.
②ME=NF.
(2)连接BM,BN,求证:四边形BMDN是菱形.
(3)若AB=4,BD=2,∠MDN=60°,求AM的长及菱形ABCD的面积.
如图,在△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE的延长线于点F,连接AE,CF.
(1)求证:四边形AECF是菱形.
(2)若CF=8,∠FAC=30°,∠B=45°,求AB的长.
考点3 正方形的性质和判定
探究:(课本改编)如图,在正方形ABCD中,E是BC边上一点,点F在AB的延长线上,且BE=BF,延长AE交CF于点M,连接BM.
(1)猜想AE与CF的关系,并证明你的结论.
(2)求证:AM⊥CF.
(3)求证:AE·ME=CE·BE.
(4)求证:∠AMB=45°.
(5)如果正方形ABCD的边长为2,E是边BC的中点,求FM的长.
(6)猜想AM,CM,BM之间的数量关系,并证明你的结论.
参考答案
回归教材·过基础
考点清单
①相等且平行 ②相等 ③平行 ④相等 ⑤平分且垂直 ⑥一组对角
基础演练
1.(1)∠ABC=90° (2)①60° ②4 16 ③20 56 (3)4
2.(1)AB=AD
(2)①6 8 10 10 ②120° 60° 30° 4 4 8
16 ③16 ④5 ⑤
(3)8 4 80
3.(1)90° 45° 90°
(2)4 4 4 4 2
(3)2 8 8
(4)30°
真题精粹·重变式
1.①②④ 2.D 3.10 4.D
5.2 解析:如图,连接HF,EG.
∵正方形ABCD的面积为4,
∴BC∥AD,BC=AD=2.
∵H,F分别为边DA,BC的中点,
∴四边形BFHA是平行四边形,
∴AB=HF=2,AB∥HF.
同理BC=EG=2,BC∥EG.
∵AB⊥BC,
∴HF⊥EG,
∴四边形EFGH的面积是EG×HF=×2×2=2.
故答案为2.
6.解析:(1)证明:如图,设AG与DE的交点为O,连接GF.
∵点A关于DE的对称点为A',
∴AO=A'O,AA'⊥DE.
∵E,F为边AB上的两个三等分点,
∴AE=EF=BF,
∴DE∥A'F.
(2)∵AA'⊥DE,
∴∠AOE=90°=∠DAE=∠ABG,
∴∠ADE+∠DEA=90°=∠DEA+∠EAO,
∴∠ADE=∠EAO.
在△ADE和△BAG中,
∴△ADE≌△BAG(ASA),
∴AE=BG,
∴BF=BG,
∴∠GFB=∠FGB=45°.
∵∠FA'G=∠FBG=90°,
∴F,B,G,A'四点共圆,
∴∠GA'B=∠GFB=45°.
(3)证明:设AE=EF=BF=BG=a,
∴AD=BC=3a,FG=a,
∴CG=2a.
在Rt△ADE中,DE===a=AG.
∵sin∠EAO=sin∠ADE,
∴=,
∴=,∴OE=a,
∴AO===a=A'O,
∴A'G=a.
∵AO=A'O,AE=EF,
∴A'F=2OE=a.
∵∠FA'G=∠FBG=90°,
∴∠A'FB+∠A'GB=180°.
∵∠A'GC+∠A'GB=180°,
∴∠A'FB=∠A'GC.
又∵==,
∴△A'FB∽△A'GC,
∴=,
∴A'C=2A'B.
7.B
核心突破·拓思维
例1 解析:(1)∵四边形ABCD是平行四边形,点E在BC的延长线上,
∴DA∥CB,即DA∥CE.
又∵DE∥AC,
∴四边形ADEC是平行四边形.
∵AC⊥BC,
∴∠ACB=∠ACE=90°,
∴平行四边形ADEC是矩形.
(2)∵在平行四边形ABCD中,AC是对角线,且AC⊥BC,
∴△ABC是直角三角形.
∵M为斜边AB的中点,且CM=5,AC=8,
∴AB=2CM=2×5=10,
∴BC===6.
由(1)可知平行四边形ADEC是矩形,AC⊥BC,DE⊥BE,
∴AC=DE=8,AD=CE=BC=6,∴BE=12,
∴S四边形ADEB===72.
变式1 C
变式2 C
变式3 证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°,
∴平行四边形OCED是矩形.
变式4 解析:(1)证明:∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD,
∴OC=OD,
∴∠ACD=∠BDC.
∵∠CDF=∠BDC,∠DCF=∠ACD,
∴∠CDF=∠DCF,
∴DF=CF.
(2)由(1)可知 DF=CF.
∵∠CDF=60°,
∴△CDF是等边三角形,
∴CD=DF=6.
∵∠CDF=∠BDC=60°,OC=OD,
∴△OCD是等边三角形,
∴OC=OD=CD=6,
∴BD=2OD=12.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴BC===6,
∴S矩形ABCD=BC·CD=6×6=36.
例2 解析:(1)①证明:∵四边形ABCD是菱形,
∴DA=DC,∠DAE=DCF,AB=CB.
∵BE=BF,∴AE=CF.
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS).
②证明:由①知△ADE≌△CDF,
∴∠ADM=∠CDN,DE=DF.
∵四边形ABCD是菱形,
∴∠DAM=∠DCN.
∵∠ADM=∠CDN,∴∠DMA=∠CND,
∴∠DMN=∠DNM,∴DM=DN,
∴DE-DM=DF-DN,∴ME=NF.
(2)证明:如图,连接BD,交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,
由(1)②知DM=DN,
∴OM=ON,
∴四边形BMDN是菱形.
(3)如图,∵四边形ABCD是菱形,BD=2,AB=4,
∴AC⊥BD,OB=OD=1,
∴OA=OC==.
∵DM=DN,∠MDN=60°,
∴∠MDO=∠NDO =30°,
∴MD=2MO,
∴DM2=(2OM)2=OM2+OD2,
即3OM2=1,
∴OM=,
∴AM=OA-OM=-,
∴S菱形ABCD=AC·BD=×2×2=2.
变式 解析:(1)证明:在△ABC中,D是AC的中点,
∴AD=DC.
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED.
在△AFD和△CED中,
∴△AFD≌△CED(AAS),∴AF=CE,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G.
由(1)知四边形AECF是菱形,
又∵CF=8,∠FAC=30°,
∴AE=CF=8,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°.
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴AG=AE=4.
∵∠B=45°,
∴∠GAB=∠B=45°,
∴AB=AG=4.
例3 解析:(1)AE=CF.
证明:∵四边形ABCD是正方形,
∴∠ABC=90°=∠CBF,AB=CB.
在△ABE和△CBF中,
∴△ABE≌△CBF(SAS),
∴AE=CF.
(2)证明:由(1)知△ABE≌△CBF,
∴∠AEB=∠F.
∵∠BEA=∠CEM,∠F+∠BCF=90°,
∴∠CEM+∠BCF=90°,
∴∠CME=90°,即AM⊥CF.
(3)证明:由(2)可知∠AEB=∠CEM,∠ABC=∠CME=90°,
∴△ABE∽△CME,∴=,
∴AE·ME=CE·BE.
(利用定弦定角证明A,B,M,C四点共圆)
(4)证明:如图1,在线段AM上截取AH=CM,连接BH.
图1
∵AM⊥CM,∴∠AMC=∠ABC=90°,
∴∠MCB+∠CEM=∠MAB+∠AEB =90°.
∵∠CEM=∠AEB,
∴∠MCB=∠MAB.
∵AH=CM,AB=BC,
∴△BCM≌△BAH(SAS),
∴BH=BM,∠CBM=∠ABH,
∴∠ABC=∠ABH+∠HBE=∠CBM+∠HBE=90°,
∴△BHM是等腰直角三角形,∴∠AMB=45°.
(5)如图2,作BH⊥AM于点H,由(4)知∠AMB=45°,
图2
∴△HBM为等腰直角三角形,HB=HM.
∵E为BC的中点,正方形ABCD的边长为2,
∴BE=CE=BF=1,
∴AE=CF===,
∴AB·BE=AE·BH,
∴BH===.
在△BHE和△CME中,
∵BE=CE,∠BHE=∠CME=90°,∠BEH=∠CEM,
∴△BHE≌△CME(AAS),
∴CM=BH=,
∴MF=CF-CM=-=.
(6)AM-CM=BM.
证明:如图3,在线段AM上截取AH=CM,连接BH.
图3
由(4)知△BHM是等腰直角三角形,
∴MH=BM,
∴AM-CM=BM.
回归教材·过基础
【考点清单】
知识点 特殊四边形的定义及性质
特殊四边形 平行四边形 矩形 菱形 正方形
图形
性质 边 对边① 对边相等且平行 四条边② , 对边③ 四条边相等, 对边平行
角 两组对角分别相等 四个角④ (都是直角) 两组对角分别相等 四个角相等 (都是直角)
对角线 互相平分 互相平分且相等 互相⑤ , 平分⑥ 互相平分且垂直、相等,平分一组对角
对称性 中心对称图形 既是中心对称图形,也是轴对称图形,有2条对称轴 既是中心对称图形,也是轴对称图形,有2条对称轴 既是中心对称图形,也是轴对称图形有4条对称轴
对称中心为对角线的交点
周长 C=2(a+b) C=2(a+b) C=4a C=4a
面积 S=ah S=ab S=ah=mn S=a2=m2
【基础演练】
1.矩形的性质与判定:
(1)如图1,在 ABCD中,AC,BD相交于点O,请添加一个条件 (写出一个即可),
使四边形ABCD是矩形.
(2)在(1)的结论下,
①若∠BAC=30°,则∠AOD= ;
②若∠ADO=60°,BD=8,则OA的长为 ,矩形ABCD的面积为 ;
③过点O作OE∥DC交BC于点E,若OE=8,BE=6,则AC的长为 ,
矩形ABCD的周长为 .
(3)如图2,在矩形ABCD中,AB=3,AD=4,对角线AC,BD相交于点O,M,N分别是OC,BC的中点,连接ON,MN,则△OMN的周长为 .
2.菱形的性质与判定:
(1)如图1,在 ABCD中,AC,BD相交于点O,请添加一个条件 (写出一个即可),
使四边形ABCD是菱形.
(2)在(1)的结论下,完成下列问题:
①若AC=12,BD=16,则AO= ,BO= ,AB= ,AD= ;
②若∠ABC=60°,AB=4,则∠BAD= ,∠BAC= ,∠ABD= ,
AC的长是 ,BD的长是 ,四边形ABCD的面积是 ,
四边形ABCD的周长是 ;
③若tan∠BAC=,AC=12,则BD的长是 ;
④若AB=10,E是CD的中点,连接OE,则OE的长是 ;
⑤过点O作OF⊥BC于点F,若AC=12,BD=16,则OF的长是 .
(3)如图2,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AH⊥BC于点H,
若cos∠ABC=,CH=4,则AH的长是 ,AC的长是 ,菱形ABCD的面积为 .
3.正方形的性质与判定:
如图1,已知在正方形ABCD中,对角线AC,BD相交于点O.
(1)∠ABC= ,∠BAC= ,∠AOD= ;
(2)若AD=4,则AB= ,BC= ,AC= ,BD= ,BO= ;
(3)若OC=2,则正方形ABCD的边长是 ,面积是 ,周长是 ;
(4)如图2,在正方形ABCD的外侧作等边△DCE,则∠EAC= .
真题精粹·重变式
考向1 矩形的性质与判定 6年4考
1.(2021·福建)如图,在矩形ABCD中,AB=4,AD=5,E,F分别是边AB,BC上的动点,点E不与点A,B重合,且EF=AB,G是五边形AEFCD内满足GE=GF且∠EGF=90°的点.现给出以下结论:
①∠GEB与∠GFB一定互补;
②点G到边AB,BC的距离一定相等;
③点G到边AD,DC的距离可能相等;
④点G到边AB距离的最大值为2.
其中正确的是 .(写出所有正确结论的序号)
热点训练 2.如图,将矩形纸片ABCD的两个直角进行折叠,使CB,AD恰好落在对角线AC上,点B',D'分别是点B,D的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段B'D'的长是 ( ) A. B.2 C. D.1
考向2 菱形的性质与判定 6年1考
3.(2023·福建)如图,在菱形ABCD中,AB=10,∠B=60°,则AC的长为 .
热点训练 4.如图,在菱形ABCD中,对角线AC与BD相交于点O,过点C作CE∥BD交AB的延长线于点E,下列结论不一定正确的是 ( ) A.OB=CE B.△ACE是直角三角形 C.BC=AE D.BE=CE
考向3 正方形的性质与判定 6年2考
5.(2024·福建)如图,正方形ABCD的面积为4,E,F,G,H分别为边AB,BC,CD,AD的中点,则四边形EFGH的面积为 .
6.(2021·福建)如图,在正方形ABCD中,E,F为边AB上的两个三等分点,点A关于DE的对称点为点A',AA'的延长线交BC于点G.
(1)求证:DE∥A'F.
(2)求∠GA'B的大小.
(3)求证:A'C=2A'B.
热点训练 7.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D'.若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是 ( ) A.1 B. C. D.
核心突破·拓思维
考点1 矩形的性质和判定
如图,在 ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,M为AB的中点,连接CM.
(1)求证:四边形ADEC是矩形.
(2)若CM=5,AC=8,求四边形ADEB的面积.
如图,在矩形ABCD中,点E在边BC上,F是AE的中点,AB=6,AD=ED=10,则BF的长为 ( )
A. B.2 C. D.2
如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,P是AD上不与点A,D重合的一个动点,过点P分别作AC和BD边上的垂线,垂足分别为E,F,则PE+PF的值为 ( )
A. B. C. D.
已知菱形ABCD的对角线AC,BD交于点O,CE∥OD,DE∥OC.求证:四边形OCED是矩形.
如图,在矩形ABCD中,对角线AC,BD相交于点O,且∠CDF=∠BDC,∠DCF=∠ACD.
(1)求证: DF=CF.
(2)若∠CDF=60°,DF=6,求矩形ABCD的面积.
考点2 菱形的性质和判定
如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
(1)求证:
①△ADE≌△CDF.
②ME=NF.
(2)连接BM,BN,求证:四边形BMDN是菱形.
(3)若AB=4,BD=2,∠MDN=60°,求AM的长及菱形ABCD的面积.
如图,在△ABC中,D是AC的中点,过点D作DE⊥AC交BC于点E,过点A作AF∥BC交DE的延长线于点F,连接AE,CF.
(1)求证:四边形AECF是菱形.
(2)若CF=8,∠FAC=30°,∠B=45°,求AB的长.
考点3 正方形的性质和判定
探究:(课本改编)如图,在正方形ABCD中,E是BC边上一点,点F在AB的延长线上,且BE=BF,延长AE交CF于点M,连接BM.
(1)猜想AE与CF的关系,并证明你的结论.
(2)求证:AM⊥CF.
(3)求证:AE·ME=CE·BE.
(4)求证:∠AMB=45°.
(5)如果正方形ABCD的边长为2,E是边BC的中点,求FM的长.
(6)猜想AM,CM,BM之间的数量关系,并证明你的结论.
参考答案
回归教材·过基础
考点清单
①相等且平行 ②相等 ③平行 ④相等 ⑤平分且垂直 ⑥一组对角
基础演练
1.(1)∠ABC=90° (2)①60° ②4 16 ③20 56 (3)4
2.(1)AB=AD
(2)①6 8 10 10 ②120° 60° 30° 4 4 8
16 ③16 ④5 ⑤
(3)8 4 80
3.(1)90° 45° 90°
(2)4 4 4 4 2
(3)2 8 8
(4)30°
真题精粹·重变式
1.①②④ 2.D 3.10 4.D
5.2 解析:如图,连接HF,EG.
∵正方形ABCD的面积为4,
∴BC∥AD,BC=AD=2.
∵H,F分别为边DA,BC的中点,
∴四边形BFHA是平行四边形,
∴AB=HF=2,AB∥HF.
同理BC=EG=2,BC∥EG.
∵AB⊥BC,
∴HF⊥EG,
∴四边形EFGH的面积是EG×HF=×2×2=2.
故答案为2.
6.解析:(1)证明:如图,设AG与DE的交点为O,连接GF.
∵点A关于DE的对称点为A',
∴AO=A'O,AA'⊥DE.
∵E,F为边AB上的两个三等分点,
∴AE=EF=BF,
∴DE∥A'F.
(2)∵AA'⊥DE,
∴∠AOE=90°=∠DAE=∠ABG,
∴∠ADE+∠DEA=90°=∠DEA+∠EAO,
∴∠ADE=∠EAO.
在△ADE和△BAG中,
∴△ADE≌△BAG(ASA),
∴AE=BG,
∴BF=BG,
∴∠GFB=∠FGB=45°.
∵∠FA'G=∠FBG=90°,
∴F,B,G,A'四点共圆,
∴∠GA'B=∠GFB=45°.
(3)证明:设AE=EF=BF=BG=a,
∴AD=BC=3a,FG=a,
∴CG=2a.
在Rt△ADE中,DE===a=AG.
∵sin∠EAO=sin∠ADE,
∴=,
∴=,∴OE=a,
∴AO===a=A'O,
∴A'G=a.
∵AO=A'O,AE=EF,
∴A'F=2OE=a.
∵∠FA'G=∠FBG=90°,
∴∠A'FB+∠A'GB=180°.
∵∠A'GC+∠A'GB=180°,
∴∠A'FB=∠A'GC.
又∵==,
∴△A'FB∽△A'GC,
∴=,
∴A'C=2A'B.
7.B
核心突破·拓思维
例1 解析:(1)∵四边形ABCD是平行四边形,点E在BC的延长线上,
∴DA∥CB,即DA∥CE.
又∵DE∥AC,
∴四边形ADEC是平行四边形.
∵AC⊥BC,
∴∠ACB=∠ACE=90°,
∴平行四边形ADEC是矩形.
(2)∵在平行四边形ABCD中,AC是对角线,且AC⊥BC,
∴△ABC是直角三角形.
∵M为斜边AB的中点,且CM=5,AC=8,
∴AB=2CM=2×5=10,
∴BC===6.
由(1)可知平行四边形ADEC是矩形,AC⊥BC,DE⊥BE,
∴AC=DE=8,AD=CE=BC=6,∴BE=12,
∴S四边形ADEB===72.
变式1 C
变式2 C
变式3 证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°,
∴平行四边形OCED是矩形.
变式4 解析:(1)证明:∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD,
∴OC=OD,
∴∠ACD=∠BDC.
∵∠CDF=∠BDC,∠DCF=∠ACD,
∴∠CDF=∠DCF,
∴DF=CF.
(2)由(1)可知 DF=CF.
∵∠CDF=60°,
∴△CDF是等边三角形,
∴CD=DF=6.
∵∠CDF=∠BDC=60°,OC=OD,
∴△OCD是等边三角形,
∴OC=OD=CD=6,
∴BD=2OD=12.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∴BC===6,
∴S矩形ABCD=BC·CD=6×6=36.
例2 解析:(1)①证明:∵四边形ABCD是菱形,
∴DA=DC,∠DAE=DCF,AB=CB.
∵BE=BF,∴AE=CF.
在△ADE和△CDF中,
∴△ADE≌△CDF(SAS).
②证明:由①知△ADE≌△CDF,
∴∠ADM=∠CDN,DE=DF.
∵四边形ABCD是菱形,
∴∠DAM=∠DCN.
∵∠ADM=∠CDN,∴∠DMA=∠CND,
∴∠DMN=∠DNM,∴DM=DN,
∴DE-DM=DF-DN,∴ME=NF.
(2)证明:如图,连接BD,交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD,
由(1)②知DM=DN,
∴OM=ON,
∴四边形BMDN是菱形.
(3)如图,∵四边形ABCD是菱形,BD=2,AB=4,
∴AC⊥BD,OB=OD=1,
∴OA=OC==.
∵DM=DN,∠MDN=60°,
∴∠MDO=∠NDO =30°,
∴MD=2MO,
∴DM2=(2OM)2=OM2+OD2,
即3OM2=1,
∴OM=,
∴AM=OA-OM=-,
∴S菱形ABCD=AC·BD=×2×2=2.
变式 解析:(1)证明:在△ABC中,D是AC的中点,
∴AD=DC.
∵AF∥BC,
∴∠FAD=∠ECD,∠AFD=∠CED.
在△AFD和△CED中,
∴△AFD≌△CED(AAS),∴AF=CE,
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴平行四边形AECF是菱形.
(2)如图,过点A作AG⊥BC于点G.
由(1)知四边形AECF是菱形,
又∵CF=8,∠FAC=30°,
∴AE=CF=8,∠FAE=2∠FAC=60°,
∴∠AEB=∠FAE=60°.
∵AG⊥BC,
∴∠AGB=∠AGE=90°,
∴∠GAE=30°,
∴AG=AE=4.
∵∠B=45°,
∴∠GAB=∠B=45°,
∴AB=AG=4.
例3 解析:(1)AE=CF.
证明:∵四边形ABCD是正方形,
∴∠ABC=90°=∠CBF,AB=CB.
在△ABE和△CBF中,
∴△ABE≌△CBF(SAS),
∴AE=CF.
(2)证明:由(1)知△ABE≌△CBF,
∴∠AEB=∠F.
∵∠BEA=∠CEM,∠F+∠BCF=90°,
∴∠CEM+∠BCF=90°,
∴∠CME=90°,即AM⊥CF.
(3)证明:由(2)可知∠AEB=∠CEM,∠ABC=∠CME=90°,
∴△ABE∽△CME,∴=,
∴AE·ME=CE·BE.
(利用定弦定角证明A,B,M,C四点共圆)
(4)证明:如图1,在线段AM上截取AH=CM,连接BH.
图1
∵AM⊥CM,∴∠AMC=∠ABC=90°,
∴∠MCB+∠CEM=∠MAB+∠AEB =90°.
∵∠CEM=∠AEB,
∴∠MCB=∠MAB.
∵AH=CM,AB=BC,
∴△BCM≌△BAH(SAS),
∴BH=BM,∠CBM=∠ABH,
∴∠ABC=∠ABH+∠HBE=∠CBM+∠HBE=90°,
∴△BHM是等腰直角三角形,∴∠AMB=45°.
(5)如图2,作BH⊥AM于点H,由(4)知∠AMB=45°,
图2
∴△HBM为等腰直角三角形,HB=HM.
∵E为BC的中点,正方形ABCD的边长为2,
∴BE=CE=BF=1,
∴AE=CF===,
∴AB·BE=AE·BH,
∴BH===.
在△BHE和△CME中,
∵BE=CE,∠BHE=∠CME=90°,∠BEH=∠CEM,
∴△BHE≌△CME(AAS),
∴CM=BH=,
∴MF=CF-CM=-=.
(6)AM-CM=BM.
证明:如图3,在线段AM上截取AH=CM,连接BH.
图3
由(4)知△BHM是等腰直角三角形,
∴MH=BM,
∴AM-CM=BM.
同课章节目录
