专题八 几何图形综合探究题 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 专题八 几何图形综合探究题 学案(含答案)2025年中考数学人教版一轮复习考点探究 |

|
|
| 格式 | docx | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览




文档简介
类型一 固定图形的证明与计算
如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF.
(1)求证:四边形AECF为菱形.
(2)若AB=8,BC=16,求菱形AECF的周长.
(1)根据ASA证明△AEO≌△CFO
OE=OF
四边形AECF是平行四边形
根据EF⊥AC判定四边形是菱形
(2)由线段垂直平分线的性质,得AF=CF
设AF=x
在Rt△ABF中,利用勾股定理列方程求解
1.已知正方形ABCD,在BC和CD边上各有一点E,F,且CE=CF,连接AF,EF,分别取AF,EF的中点M,N,连接DM,CN,MN.
图1 图2
(1)如图1,连接AE.
①求证:AE=AF.
②求∠DMN的度数.
(2)如图2,将△CEF绕点C旋转,当△CEF在正方形ABCD外部时,连接DN,试探究DN与MN的数量关系,并说明理由.
类型二 与动点问题有关的证明与计算
如图,菱形ABCD的边长为4,E,F分别是边BC,CD上的动点,∠BAC=∠EAF=60°,连接EF,交AC于点G.
(1)求证:AE=AF.
(2)求△ECF周长的最小值.
(3)若BE=1,求CG的长.
(1)根据菱形的性质得△ABC是等边三角形
利用ASA证明△ABE≌△ACF
可证明结论
(2)证明△AEF是等边三角形
将△ECF的周长转化为EF+BC
求EF的最小值即可
(3)证明△CEG∽△BAE
根据对应边成比例可得CG的长
2.如图,在正方形ABCD中,AB=3,M为CD边上的一动点(不与点D重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(备用图)
(1)依题意补全图形.
(2)若DM=1,求线段EF的长.
(3)当点M在CD边上运动时,若△AEF为等腰三角形,求DM的长.
类型三 图形旋转、平移、折叠变换
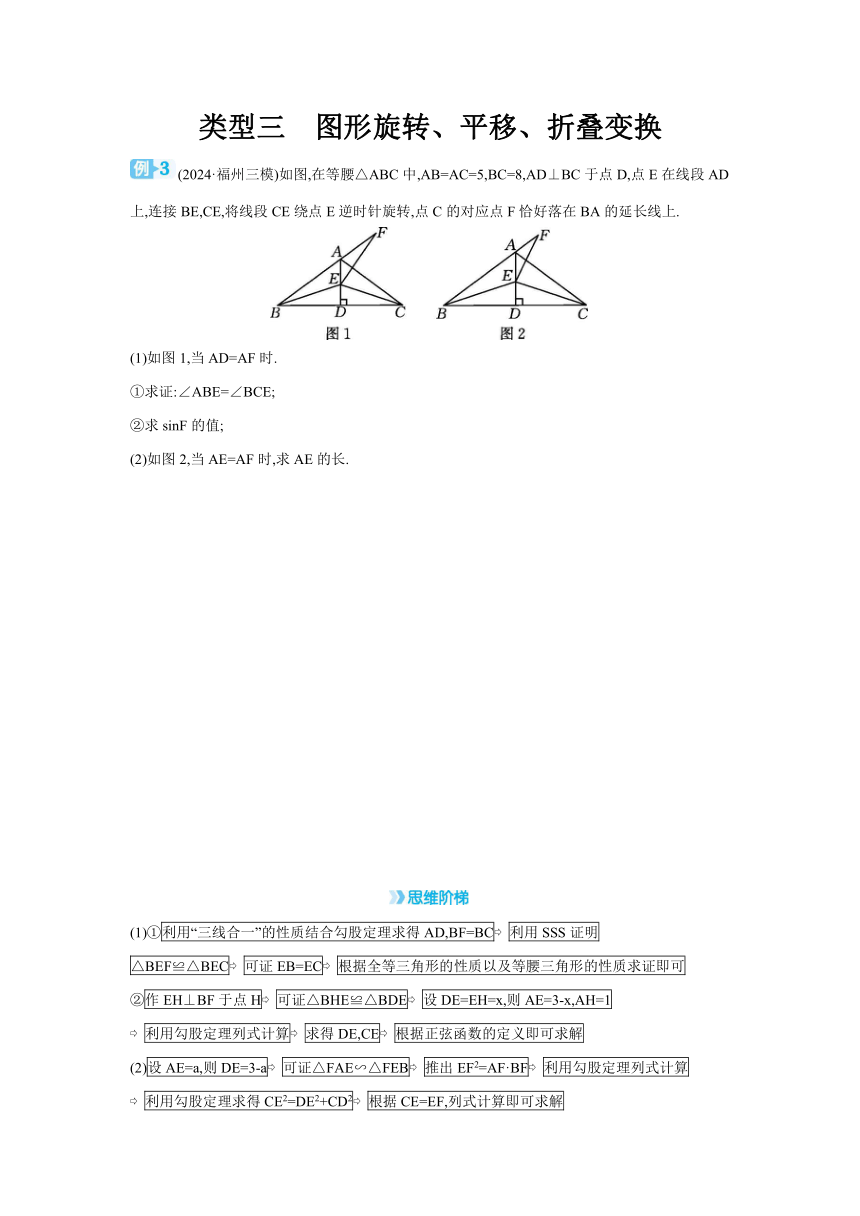
(2024·福州三模)如图,在等腰△ABC中,AB=AC=5,BC=8,AD⊥BC于点D,点E在线段AD上,连接BE,CE,将线段CE绕点E逆时针旋转,点C的对应点F恰好落在BA的延长线上.
(1)如图1,当AD=AF时.
①求证:∠ABE=∠BCE;
②求sinF的值;
(2)如图2,当AE=AF时,求AE的长.
(1)①利用“三线合一”的性质结合勾股定理求得AD,BF=BC 利用SSS证明
△BEF≌△BEC 可证EB=EC 根据全等三角形的性质以及等腰三角形的性质求证即可
②作EH⊥BF于点H 可证△BHE≌△BDE 设DE=EH=x,则AE=3-x,AH=1
利用勾股定理列式计算 求得DE,CE 根据正弦函数的定义即可求解
(2)设AE=a,则DE=3-a 可证△FAE∽△FEB 推出EF2=AF·BF 利用勾股定理列式计算
利用勾股定理求得CE2=DE2+CD2 根据CE=EF,列式计算即可求解
3.如图1,在矩形ABCD中,AB=6,AD=8,点P在边BC上,且不与点B,C重合.将△APB沿直线AP折叠得到△APB',点B'落在矩形ABCD的内部,延长PB'交直线AD于点F.
(1)求证:FA=FP.
(2)①当P是BC的中点时,求AF的长;
②如图2,直线AP与DC的延长线交于点E,连接BB'交AE于点H,G是AE的中点.当∠EAB'=2∠AEB'时,请判断AB与HG的数量关系,并说明理由.
参考答案
例1 解析:(1)证明:∵EF是AC的垂直平分线,
∴AO=OC,∠AOE=∠COF=90°.
∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO.
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA),∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
又∵EF⊥AC,∴平行四边形AECF是菱形.
(2)设AF=x.
∵EF是AC的垂直平分线,AB=8,BC=16,∴AF=CF=x,BF=16-x.
在Rt△ABF中,由勾股定理,得AB2+BF2=AF2,
即82+(16-x)2=x2,解得x=10,∴AF=10,
∴菱形AECF的周长为40.
针对训练 1.解析:(1)①证明:∵四边形ABCD是正方形,
∴AB=AD=BC=DC,∠ABE=∠ADF=90°.
∵CE=CF,∴BC-CE=DC-CF,∴BE=DF.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
②∵∠ADF=90°,M,N分别是AF,EF的中点,
∴DM=AM=FM=AF,MN∥AE,
∴∠MDA=∠DAF,∠FMN=∠FAE.
∵△ABE≌△ADF,∴∠BAE=∠DAF,
∴∠MDA=∠BAE,
∴∠FMD=∠DAF+∠MDA=∠DAF+∠BAE,
∴∠DMN=∠FMD+∠FMN=∠DAF+∠BAE+∠FAE=∠DAB=90°.
(2)DN=MN.理由:如图,连接AC,AE.
∵M,N分别是AF,EF的中点,
∴AE=2MN.
∵CE=CF,∠ECF=90°,∴CN⊥EF,CN=EN=FN=EF,
∴∠CNE=90°,∴∠NCE=∠NEC=45°.
∵AD=CD,∠ADC=90°,∴∠DCA=∠DAC=45°,
∴==sin 45°=.
∵∠DCN=∠ACE=45°+∠DCE,
∴△DCN∽△ACE,
∴==,∴=,∴DN=MN.
例2 解析:(1)证明:∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF.
∵四边形ABCD是菱形,∴AB=BC,AB∥CD,
∴△ABC是等边三角形,∠ACD=∠BAC=60°,
∴AB=AC,∠B=60°,∴∠B=∠ACD,
∴△ABE≌△ACF(ASA),∴AE=AF.
(2)∵△ABE≌△ACF,∴BE=CF.
∵菱形ABCD的边长为4,
∴△ECF的周长=EC+CF+EF=EC+BE+EF=BC+EF=4+EF,
∴当EF最小时,△ECF的周长最小.
∵AE=AF,∠EAF=60°,∴△AEF是等边三角形,
∴AE=EF,
即当AE最小时,△ECF的周长最小,最小值为4+AE.
∵E是BC边上的动点,∴当AE⊥BC时,AE最小.
在Rt△ABE中,AB=4,∠B=60°,∴AE=2,
∴△ECF周长的最小值为4+2.
(3)∵四边形ABCD是菱形,∠BAC=∠EAF=60°,
∴AB=BC,
∴△ABC是等边三角形,∴∠ABC=∠BCA=60°.
由(2)知△AEF是等边三角形,∴∠AEF=60°,
∴∠BAE=180°-60°-∠BEA=∠CEG,
∴△CEG∽△BAE,
∴=,∴=,∴CG=.
针对训练 2.解析:(1)补全图形如图1所示.
图1
(2)如图2,连接BM.
图2
∵点D与点E关于AM所在的直线对称,∴AE=AD,∠MAD=∠MAE.
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°.
∵DM=BF,∴△ADM≌△ABF(SAS),
∴AF=AM,∠FAB=∠MAD,∴∠FAB=∠MAE,
∴∠FAE=∠MAB.
又∵AB=AE=AD,
∴△FAE≌△MAB(SAS),∴EF=BM.
∵四边形ABCD是正方形,∴BC=CD=AB=3.
∵DM=1,∴CM=2,∴BM==,
∴EF=.
故线段EF的长为.
(3)设DM=x(x>0),则CM=3-x,
∴EF=BM==.
∵AE=AD=3,AF=AM==,
∴AF>AE,∴当△AEF为等腰三角形时,只能有两种情况AE=EF,或AF=EF,
①当AE=EF时,有=3,解得x=3;
②当AF=EF时,=,解得x=.
综上所述,当△AEF为等腰三角形时,DM=3或.
例3 解析:(1)①证明:∵AB=AC,BC=8,AD⊥BC于点D,
∴BD=CD=BC=4,
∴AD==3,
∴AF=3,
∴BF=8,
∴BF=BC.
∵BE=BE,EF=EC,
∴△BEF≌△BEC(SSS),
∴∠ABE=∠EBC.
∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线,
∴EB=EC,
∴∠EBC=∠ECB,
∴∠ABE=∠BCE.
②如图,作EH⊥BF于点H,即∠BHE=90°,
∵△BEF≌△BEC,
∴∠ABE=∠DBE,∠F=∠ECB.
∵∠BHE=∠BDE=90°,BE=BE,
∴△BHE≌△BDE,
∴DE=EH,BH=BD=4.
设DE=EH=x,
∴AE=3-x,AH=AB-BH=1.
∵AH2+EH2=AE2,
∴12+x2=(3-x)2,
解得x=,
∴DE=,
∴CE===,
∴sinF=sin∠ECD==.
(2)设AE=a,则DE=3-a.
∵AE=AF,
∴AF=a,∠F=∠AEF.
∵AD垂直平分BC,
∴BE=CE,
由旋转得CE=EF,
∴BE=EF,
∴∠F=∠ABE,
∴∠AEF=∠ABE.
又∵∠F=∠F,
∴△FAE∽△FEB,
∴=,
∴EF2=AF·BF.
∵CE2=DE2+CD2,
∴CE2=(3-a)2+42,EF2=a(5+a).
∵CE=EF,
∴a(5+a)=(3-a)2+42,
解得a=,
∴AE=.
针对训练 3.解析:(1)证明:由折叠性质可得∠APB=∠APF.
∵四边形ABCD是矩形,
∴AD∥BC,∴∠APB=∠FAP,
∴∠APF=∠FAP,∴FA=FP.
(2)①由题意知,B'P=BP=BC=4,AB'=AB=6.
设AF=FP=x,则B'F=x-4,
在Rt△AB'F中,由勾股定理得AF2-B'F2=AB'2,即x2-(x-4)2=62,解得x=,
∴AF的长为.
②AB与HG的数量关系为AB=2HG.
理由:如图,过点B'作B'M∥CD,交AE于点M,
∴∠AMB'=∠AED.
由折叠的性质可得,∠BAP=∠EAB',AH⊥BB'.
∵AB∥CD,∴∠BAP=∠AED,
∴∠AMB'=∠EAB',∴B'M=AB'=AB.
由题意可知△ABH≌△MB'H,∴AH=HM,H是AM的中点,∴AH=AM.
∵∠EAB'=2∠AEB',∴∠AMB'=∠EAB'=2∠AEB'.
∵∠AMB'=∠EB'M+∠AEB',∴∠EB'M=∠AEB',∴ME=B'M=AB.
∵G是AE的中点,∴AG=AE,
∴HG=AG-AH=AE-AM=ME=AB,∴AB=2HG,
∴AB与HG的数量关系为AB=2HG.
如图,在矩形ABCD中,对角线AC的垂直平分线EF分别交AD,AC,BC于点E,O,F,连接CE和AF.
(1)求证:四边形AECF为菱形.
(2)若AB=8,BC=16,求菱形AECF的周长.
(1)根据ASA证明△AEO≌△CFO
OE=OF
四边形AECF是平行四边形
根据EF⊥AC判定四边形是菱形
(2)由线段垂直平分线的性质,得AF=CF
设AF=x
在Rt△ABF中,利用勾股定理列方程求解
1.已知正方形ABCD,在BC和CD边上各有一点E,F,且CE=CF,连接AF,EF,分别取AF,EF的中点M,N,连接DM,CN,MN.
图1 图2
(1)如图1,连接AE.
①求证:AE=AF.
②求∠DMN的度数.
(2)如图2,将△CEF绕点C旋转,当△CEF在正方形ABCD外部时,连接DN,试探究DN与MN的数量关系,并说明理由.
类型二 与动点问题有关的证明与计算
如图,菱形ABCD的边长为4,E,F分别是边BC,CD上的动点,∠BAC=∠EAF=60°,连接EF,交AC于点G.
(1)求证:AE=AF.
(2)求△ECF周长的最小值.
(3)若BE=1,求CG的长.
(1)根据菱形的性质得△ABC是等边三角形
利用ASA证明△ABE≌△ACF
可证明结论
(2)证明△AEF是等边三角形
将△ECF的周长转化为EF+BC
求EF的最小值即可
(3)证明△CEG∽△BAE
根据对应边成比例可得CG的长
2.如图,在正方形ABCD中,AB=3,M为CD边上的一动点(不与点D重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(备用图)
(1)依题意补全图形.
(2)若DM=1,求线段EF的长.
(3)当点M在CD边上运动时,若△AEF为等腰三角形,求DM的长.
类型三 图形旋转、平移、折叠变换
(2024·福州三模)如图,在等腰△ABC中,AB=AC=5,BC=8,AD⊥BC于点D,点E在线段AD上,连接BE,CE,将线段CE绕点E逆时针旋转,点C的对应点F恰好落在BA的延长线上.
(1)如图1,当AD=AF时.
①求证:∠ABE=∠BCE;
②求sinF的值;
(2)如图2,当AE=AF时,求AE的长.
(1)①利用“三线合一”的性质结合勾股定理求得AD,BF=BC 利用SSS证明
△BEF≌△BEC 可证EB=EC 根据全等三角形的性质以及等腰三角形的性质求证即可
②作EH⊥BF于点H 可证△BHE≌△BDE 设DE=EH=x,则AE=3-x,AH=1
利用勾股定理列式计算 求得DE,CE 根据正弦函数的定义即可求解
(2)设AE=a,则DE=3-a 可证△FAE∽△FEB 推出EF2=AF·BF 利用勾股定理列式计算
利用勾股定理求得CE2=DE2+CD2 根据CE=EF,列式计算即可求解
3.如图1,在矩形ABCD中,AB=6,AD=8,点P在边BC上,且不与点B,C重合.将△APB沿直线AP折叠得到△APB',点B'落在矩形ABCD的内部,延长PB'交直线AD于点F.
(1)求证:FA=FP.
(2)①当P是BC的中点时,求AF的长;
②如图2,直线AP与DC的延长线交于点E,连接BB'交AE于点H,G是AE的中点.当∠EAB'=2∠AEB'时,请判断AB与HG的数量关系,并说明理由.
参考答案
例1 解析:(1)证明:∵EF是AC的垂直平分线,
∴AO=OC,∠AOE=∠COF=90°.
∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO.
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA),∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
又∵EF⊥AC,∴平行四边形AECF是菱形.
(2)设AF=x.
∵EF是AC的垂直平分线,AB=8,BC=16,∴AF=CF=x,BF=16-x.
在Rt△ABF中,由勾股定理,得AB2+BF2=AF2,
即82+(16-x)2=x2,解得x=10,∴AF=10,
∴菱形AECF的周长为40.
针对训练 1.解析:(1)①证明:∵四边形ABCD是正方形,
∴AB=AD=BC=DC,∠ABE=∠ADF=90°.
∵CE=CF,∴BC-CE=DC-CF,∴BE=DF.
在△ABE和△ADF中,
∴△ABE≌△ADF(SAS),
∴AE=AF.
②∵∠ADF=90°,M,N分别是AF,EF的中点,
∴DM=AM=FM=AF,MN∥AE,
∴∠MDA=∠DAF,∠FMN=∠FAE.
∵△ABE≌△ADF,∴∠BAE=∠DAF,
∴∠MDA=∠BAE,
∴∠FMD=∠DAF+∠MDA=∠DAF+∠BAE,
∴∠DMN=∠FMD+∠FMN=∠DAF+∠BAE+∠FAE=∠DAB=90°.
(2)DN=MN.理由:如图,连接AC,AE.
∵M,N分别是AF,EF的中点,
∴AE=2MN.
∵CE=CF,∠ECF=90°,∴CN⊥EF,CN=EN=FN=EF,
∴∠CNE=90°,∴∠NCE=∠NEC=45°.
∵AD=CD,∠ADC=90°,∴∠DCA=∠DAC=45°,
∴==sin 45°=.
∵∠DCN=∠ACE=45°+∠DCE,
∴△DCN∽△ACE,
∴==,∴=,∴DN=MN.
例2 解析:(1)证明:∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF.
∵四边形ABCD是菱形,∴AB=BC,AB∥CD,
∴△ABC是等边三角形,∠ACD=∠BAC=60°,
∴AB=AC,∠B=60°,∴∠B=∠ACD,
∴△ABE≌△ACF(ASA),∴AE=AF.
(2)∵△ABE≌△ACF,∴BE=CF.
∵菱形ABCD的边长为4,
∴△ECF的周长=EC+CF+EF=EC+BE+EF=BC+EF=4+EF,
∴当EF最小时,△ECF的周长最小.
∵AE=AF,∠EAF=60°,∴△AEF是等边三角形,
∴AE=EF,
即当AE最小时,△ECF的周长最小,最小值为4+AE.
∵E是BC边上的动点,∴当AE⊥BC时,AE最小.
在Rt△ABE中,AB=4,∠B=60°,∴AE=2,
∴△ECF周长的最小值为4+2.
(3)∵四边形ABCD是菱形,∠BAC=∠EAF=60°,
∴AB=BC,
∴△ABC是等边三角形,∴∠ABC=∠BCA=60°.
由(2)知△AEF是等边三角形,∴∠AEF=60°,
∴∠BAE=180°-60°-∠BEA=∠CEG,
∴△CEG∽△BAE,
∴=,∴=,∴CG=.
针对训练 2.解析:(1)补全图形如图1所示.
图1
(2)如图2,连接BM.
图2
∵点D与点E关于AM所在的直线对称,∴AE=AD,∠MAD=∠MAE.
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°.
∵DM=BF,∴△ADM≌△ABF(SAS),
∴AF=AM,∠FAB=∠MAD,∴∠FAB=∠MAE,
∴∠FAE=∠MAB.
又∵AB=AE=AD,
∴△FAE≌△MAB(SAS),∴EF=BM.
∵四边形ABCD是正方形,∴BC=CD=AB=3.
∵DM=1,∴CM=2,∴BM==,
∴EF=.
故线段EF的长为.
(3)设DM=x(x>0),则CM=3-x,
∴EF=BM==.
∵AE=AD=3,AF=AM==,
∴AF>AE,∴当△AEF为等腰三角形时,只能有两种情况AE=EF,或AF=EF,
①当AE=EF时,有=3,解得x=3;
②当AF=EF时,=,解得x=.
综上所述,当△AEF为等腰三角形时,DM=3或.
例3 解析:(1)①证明:∵AB=AC,BC=8,AD⊥BC于点D,
∴BD=CD=BC=4,
∴AD==3,
∴AF=3,
∴BF=8,
∴BF=BC.
∵BE=BE,EF=EC,
∴△BEF≌△BEC(SSS),
∴∠ABE=∠EBC.
∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线,
∴EB=EC,
∴∠EBC=∠ECB,
∴∠ABE=∠BCE.
②如图,作EH⊥BF于点H,即∠BHE=90°,
∵△BEF≌△BEC,
∴∠ABE=∠DBE,∠F=∠ECB.
∵∠BHE=∠BDE=90°,BE=BE,
∴△BHE≌△BDE,
∴DE=EH,BH=BD=4.
设DE=EH=x,
∴AE=3-x,AH=AB-BH=1.
∵AH2+EH2=AE2,
∴12+x2=(3-x)2,
解得x=,
∴DE=,
∴CE===,
∴sinF=sin∠ECD==.
(2)设AE=a,则DE=3-a.
∵AE=AF,
∴AF=a,∠F=∠AEF.
∵AD垂直平分BC,
∴BE=CE,
由旋转得CE=EF,
∴BE=EF,
∴∠F=∠ABE,
∴∠AEF=∠ABE.
又∵∠F=∠F,
∴△FAE∽△FEB,
∴=,
∴EF2=AF·BF.
∵CE2=DE2+CD2,
∴CE2=(3-a)2+42,EF2=a(5+a).
∵CE=EF,
∴a(5+a)=(3-a)2+42,
解得a=,
∴AE=.
针对训练 3.解析:(1)证明:由折叠性质可得∠APB=∠APF.
∵四边形ABCD是矩形,
∴AD∥BC,∴∠APB=∠FAP,
∴∠APF=∠FAP,∴FA=FP.
(2)①由题意知,B'P=BP=BC=4,AB'=AB=6.
设AF=FP=x,则B'F=x-4,
在Rt△AB'F中,由勾股定理得AF2-B'F2=AB'2,即x2-(x-4)2=62,解得x=,
∴AF的长为.
②AB与HG的数量关系为AB=2HG.
理由:如图,过点B'作B'M∥CD,交AE于点M,
∴∠AMB'=∠AED.
由折叠的性质可得,∠BAP=∠EAB',AH⊥BB'.
∵AB∥CD,∴∠BAP=∠AED,
∴∠AMB'=∠EAB',∴B'M=AB'=AB.
由题意可知△ABH≌△MB'H,∴AH=HM,H是AM的中点,∴AH=AM.
∵∠EAB'=2∠AEB',∴∠AMB'=∠EAB'=2∠AEB'.
∵∠AMB'=∠EB'M+∠AEB',∴∠EB'M=∠AEB',∴ME=B'M=AB.
∵G是AE的中点,∴AG=AE,
∴HG=AG-AH=AE-AM=ME=AB,∴AB=2HG,
∴AB与HG的数量关系为AB=2HG.
同课章节目录
