专题二 尺规作图 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 专题二 尺规作图 学案(含答案)2025年中考数学人教版一轮复习考点探究 |

|
|
| 格式 | docx | ||
| 文件大小 | 243.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览




文档简介
类型一 直接(指令性)基本作图
如图,线段AC,BD相交于点O, 且AB∥CD,AE⊥BD于点E.
(1)尺规作图:过点C作BD的垂线,垂足为F,连接AF,CE.(不写作法,保留作图痕迹,并标明相应的字母)
(2)若AB=CD,请判断四边形AECF的形状,并说明理由.(若前问未完成,可画草图完成此问)
1.如图,根据△ABC中尺规作图的痕迹,下列说法不一定正确的是 ( )
A.AF=BF B.AE=AC
C.∠DBF+∠DFB=90° D.∠BAF=∠EBC
2.如图,在△ABC中,∠ABC的平分线交AC于点F.
(1)用尺规作图法在直线BC上求作点E,使AE∥BF,不写作法,保留作图痕迹.
(2)若AB=4,BC=5,AC=6,求AF的长.
3.如图,在△ABC中,点P,Q分别在边BC及CB的延长线上,且BQ=CP.
(1)实践与探索:利用尺规按下列要求作图(不写作法,保留作图痕迹).
①作∠PQM=∠CBA,且点M在QC的上方;
②在QM上截取QR=BA;
③连接PR.
猜想与验证:试猜想线段AC和RP的数量关系,并证明你的猜想.
类型二 选择规则性(理解性、应用性)尺规作图
如图,在△ABC中,I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E.(要求:尺规作图,不写作法,保留作图痕迹)
(2)若AB=6,AC=8,DE=,求BC的长.
4.求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:如图,D,E分别是△ABC的边AB,AC的中点,连接DE.
求证:DE∥BC,且DE=BC.
(要求:尺规作图画出点D和点E,只保留作图痕迹,不写作法)
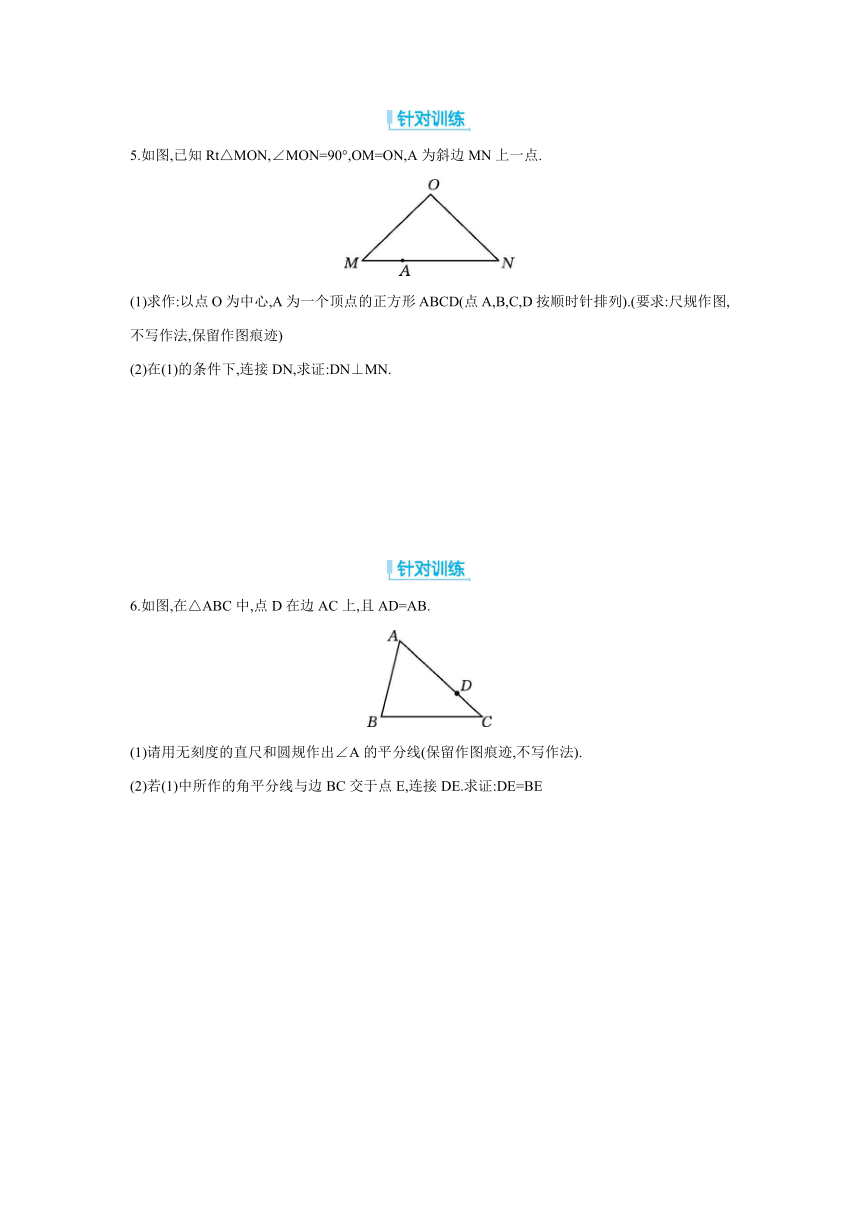
5.如图,已知Rt△MON,∠MON=90°,OM=ON,A为斜边MN上一点.
(1)求作:以点O为中心,A为一个顶点的正方形ABCD(点A,B,C,D按顺时针排列).(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接DN,求证:DN⊥MN.
6.如图,在△ABC中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法).
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE
类型三 尺规作图与证明(计算)
如图,在等边△ABC中,D为BC边上一点,DC(1)在图中求作四边形BCEF,使得点F在边AB上,且BF=2DC,点E与点D关于AC对称.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,设EF与AD交于点G,求∠DGE的度数.
7.如图,在△ABC中,∠C=90°.
(1)求作☉O分别与AC,BC相切,使得圆心O落在AB上.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,已知OA=1,OB=2,求tanB的值.
8.(原创)如图,在△ABC中,AB=AC,且AB>BC.
(1)求作△EDC≌△ABC,使得点D在线段AB上,点E在直线AC右侧.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,延长CB至点P,使得BP=BC,连接DP,若AD=BD,求证:P,D,E三点共线.
9.如图,已知∠PAQ及AP边上一点C.
(1)用无刻度直尺和圆规在射线AQ上求作点O,使得∠COQ=2∠CAQ.(保留作图痕迹,不写作法)
(2)在(1)的条件下,以点O为圆心,以OA的长为半径的圆交射线AQ于点B,用无刻度直尺和圆规在射线CP上求作点M,使点M到点C的距离与点M到射线AQ的距离相等.(保留作图痕迹,不写作法)
(3)在(1)(2)的条件下,若sinA=,CM=12,求BM的长.
10.如图,在△ABC中,AB=AC.
(1)在线段AC上求作点D,使点D到AB和BC的距离相等.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图形中,连接BD,若AD=BD,求∠A的度数.
11.如图,在Rt△ABC中,∠BCA=90°,AD平分∠BAC交BC于点D.
(1)尺规作图:求作☉O,使得圆心O在AB上,且☉O经过A,D两点.
(2)求证:直线BC是☉O的切线.
参考答案
例1 解析:(1)下图即所求.
(2)四边形AECF是平行四边形.理由如下:
∵AB∥CD,
∴∠B=∠D,∠OAB=∠OCD.
又∵AB=CD,
∴△ABO≌△CDO(ASA),
∴OA=OC.
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEO=∠CFO=90°.
又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
针对训练 1.B
针对训练 2.解析:(1)如图,点E即所求.
(2)∵BF∥AE,
∴∠AEB=∠FBC,∠EAB=∠ABF.
∵BF是∠ABC的平分线,
∴∠FBC=∠ABF,
∴∠AEB=∠EAB,
∴BE=AB=4.
根据平行线分线段成比例定理可知===,
∴AF=AC=×6=.
针对训练 3.解析:(1)下图即所求.
(2)AC=RP.
理由:∵BQ=CP,∴BQ+BP=CP+BP,∴QP=BC.
由作图过程可知∠PQM=∠CBA,QR=AB,
∴△PQR≌△CBA(SAS),∴AC=RP.
例2 解析:(1)如图,连接BI,作∠DIB=∠IBC,直线ID交AC于点E,则直线DE为所求.
(2)如图,连接CI.
∵I是△ABC的内心,
∴BI平分∠ABC,CI平分∠ACB,
∴∠DBI=∠CBI,∠ECI=∠BCI.
∵DE∥BC,∴∠DIB=∠CBI,∠EIC=∠BCI,
∴∠DIB=∠DBI,∠EIC=∠ECI,
∴DB=DI,EI=EC.
设BD=x,则DI=x,CE=EI=-x.
∵DE∥BC,∴BD∶BA=CE∶CA,即x∶6=-x∶8,解得x=2,
∴AD=AB-BD=4.
∵DE∥BC,∴△ADE∽△ABC,∴DE∶BC=AD∶AB,即∶BC=4∶6,
解得BC=7,即BC的长为7.
针对训练 4.解析:分别作线段AB和线段AC的垂直平分线,交点分别为D和E,延长DE到点F,使EF=DE,连接FC,如图所示.
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(SAS),
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC.
针对训练 5.解析:(1)如图,四边形ABCD即所作.
(2)证明:∵∠MON=90°,OM=ON,
∴∠OMN=∠ONM=45°.
由作图可得OA=OD,∠AOD=90°=∠MON,
∴∠MOA=∠NOD,
∴△OAM≌△ODN,
∴∠OND=∠OMA=45°,
∴∠AND=∠OND+∠ONM=45°+45°=90°,
∴DN⊥MN.
针对训练 6.解析:(1)如图,AE即所求.
(2)证明:∵AE平分∠BAC,
∴∠BAE=∠DAE.
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),
∴DE=BE.
例3 解析:(1)如图1,四边形BCEF即所求.
图1
(2)如图2,取BF的中点T,连接CT,TE,设AD交CT于点J.
图2
∵∠ACB=∠ACE=∠CAB=60°,CD=CE,
∴AB∥CE.
∵FT=CD,
∴EC=FT,
∴四边形ECTF是平行四边形,
∴EF∥CT,
∴∠DGE=∠CJD.
∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACD=60°.
∵BF=2CD,BT=TF,
∴BT=CD.
在△ACD和△CBT中,
∴△ACD≌△CBT(SAS),
∴∠CAD=∠BCT,
∴∠CJD=∠CAD+∠ACJ=∠BCT+∠ACJ=60°,
∴∠DGE=∠CJD=60°.
针对训练 7.解析:(1)如图,作∠ACB的平分线CO,交AB于点O,过点O作BC的垂线,垂足为N,以点O为圆心,ON的长为半径画圆,作OM⊥AC于点M,
由作图可得BC是☉O的切线,
由角平分线的性质可得OM=ON,
∴AC是☉O的切线,
∴☉O即所求.
(2)由(1)得OM⊥AC,ON⊥BC,OM=ON.
∵∠ACB=90°,
又∵OA=1,OB=2,
∴===,
∴tanB==.
针对训练 8.解析:(1)如图1,△EDC即所求.
图1
(2)证明:如图2,连接AE,PE,设PE与AB交于点D'.
图2
∵△ABC≌△EDC,
∴AC=EC,∠ACB=∠ECD,
∴∠BCD=∠ACE.
∵AB=AC,∴∠ABC=∠ACB,AB=EC,
∴∠BAC=180°-2∠ABC.
∵CB=CD,∴∠CBD=∠CDB,
∴∠BCD=180°-2∠CBD,∴∠BAC=∠BCD,
∴∠BAC=∠ACE.
又∵AC=CA,∴△BAC≌△ECA(SAS),
∴∠ACB=∠CAE,BC=AE,∴AE∥BC,
∴∠AED'=∠P,∠EAD'=∠PBD'.
∵BP=BC,BC=AE,∴AE=BP,
∴△AD'E≌△BD'P(ASA),∴AD'=BD',
∴D'是线段AB的中点.
∵D是线段AB的中点,
∴D',D为同一个点,
∴P,D,E三点共线.
针对训练 9.解析:(1)(作法不唯一)如图1,
∴∠COQ=2∠CAQ;
点O即所求
(2)如图2,连接BC,以点B为圆心,以BC的长为半径画弧交AQ于点B1,以点B1为圆心,以任意长为半径画弧交AQ于点C1,D1,分别以点C1,D1为圆心,以大于C1D1的长为半径画弧,交于点F1,连接B1F1并延长交AP于点M.
∵AB是直径,
∴∠ACB=90°,即BC⊥AP,
根据作图可得B1C1=B1D1,C1F1=D1F1,
∴MB1⊥AQ,即∠MB1B=90°,MB1是点M到AQ的距离.
∵BC=BB1,
∴Rt△BCM≌Rt△BB1M(HL),
∴CM=B1M,
点M即所求.
(3)如图3,根据作图可得∠COQ=2∠CAQ,MC=MW=12,MW⊥AQ,连接BC,
∴在Rt△AMW中,sinA==,
∴AM===20,
∴AC=AM-CM=20-12=8.
∵AB是直径,
∴∠ACB=90°,
∴sinA==,
设BC=3x,则AB=5x,
∴在Rt△ABC中,(5x)2=(3x)2+82,
解得x=2(负值舍去),
∴BC=3x=6,
在Rt△BCM中,BM===6.
针对训练 10.解析:(1)如图,作∠ABC的平分线交AC于点D,点D即所求.
(2)∵AB=AC,∴∠ABC=∠C.
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵AD=BD,∴∠A=∠ABD,
∴∠ABC=∠C=2∠A.
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+2∠A=180°,∴∠A=36°.
针对训练 11.解析:(1)如图,☉O即所求.
(2)证明:如图,连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠CAD=∠ADO,
∴AC∥OD,
∴∠ODB=∠C=90°,∴OD⊥BC.
∵OD是半径,∴BC是☉O的切线.
如图,线段AC,BD相交于点O, 且AB∥CD,AE⊥BD于点E.
(1)尺规作图:过点C作BD的垂线,垂足为F,连接AF,CE.(不写作法,保留作图痕迹,并标明相应的字母)
(2)若AB=CD,请判断四边形AECF的形状,并说明理由.(若前问未完成,可画草图完成此问)
1.如图,根据△ABC中尺规作图的痕迹,下列说法不一定正确的是 ( )
A.AF=BF B.AE=AC
C.∠DBF+∠DFB=90° D.∠BAF=∠EBC
2.如图,在△ABC中,∠ABC的平分线交AC于点F.
(1)用尺规作图法在直线BC上求作点E,使AE∥BF,不写作法,保留作图痕迹.
(2)若AB=4,BC=5,AC=6,求AF的长.
3.如图,在△ABC中,点P,Q分别在边BC及CB的延长线上,且BQ=CP.
(1)实践与探索:利用尺规按下列要求作图(不写作法,保留作图痕迹).
①作∠PQM=∠CBA,且点M在QC的上方;
②在QM上截取QR=BA;
③连接PR.
猜想与验证:试猜想线段AC和RP的数量关系,并证明你的猜想.
类型二 选择规则性(理解性、应用性)尺规作图
如图,在△ABC中,I是△ABC的内心.
(1)求作过点I且平行于BC的直线,与AB,AC分别相交于点D,E.(要求:尺规作图,不写作法,保留作图痕迹)
(2)若AB=6,AC=8,DE=,求BC的长.
4.求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
已知:如图,D,E分别是△ABC的边AB,AC的中点,连接DE.
求证:DE∥BC,且DE=BC.
(要求:尺规作图画出点D和点E,只保留作图痕迹,不写作法)
5.如图,已知Rt△MON,∠MON=90°,OM=ON,A为斜边MN上一点.
(1)求作:以点O为中心,A为一个顶点的正方形ABCD(点A,B,C,D按顺时针排列).(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接DN,求证:DN⊥MN.
6.如图,在△ABC中,点D在边AC上,且AD=AB.
(1)请用无刻度的直尺和圆规作出∠A的平分线(保留作图痕迹,不写作法).
(2)若(1)中所作的角平分线与边BC交于点E,连接DE.求证:DE=BE
类型三 尺规作图与证明(计算)
如图,在等边△ABC中,D为BC边上一点,DC
(2)在(1)的条件下,设EF与AD交于点G,求∠DGE的度数.
7.如图,在△ABC中,∠C=90°.
(1)求作☉O分别与AC,BC相切,使得圆心O落在AB上.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,已知OA=1,OB=2,求tanB的值.
8.(原创)如图,在△ABC中,AB=AC,且AB>BC.
(1)求作△EDC≌△ABC,使得点D在线段AB上,点E在直线AC右侧.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,延长CB至点P,使得BP=BC,连接DP,若AD=BD,求证:P,D,E三点共线.
9.如图,已知∠PAQ及AP边上一点C.
(1)用无刻度直尺和圆规在射线AQ上求作点O,使得∠COQ=2∠CAQ.(保留作图痕迹,不写作法)
(2)在(1)的条件下,以点O为圆心,以OA的长为半径的圆交射线AQ于点B,用无刻度直尺和圆规在射线CP上求作点M,使点M到点C的距离与点M到射线AQ的距离相等.(保留作图痕迹,不写作法)
(3)在(1)(2)的条件下,若sinA=,CM=12,求BM的长.
10.如图,在△ABC中,AB=AC.
(1)在线段AC上求作点D,使点D到AB和BC的距离相等.(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)所作的图形中,连接BD,若AD=BD,求∠A的度数.
11.如图,在Rt△ABC中,∠BCA=90°,AD平分∠BAC交BC于点D.
(1)尺规作图:求作☉O,使得圆心O在AB上,且☉O经过A,D两点.
(2)求证:直线BC是☉O的切线.
参考答案
例1 解析:(1)下图即所求.
(2)四边形AECF是平行四边形.理由如下:
∵AB∥CD,
∴∠B=∠D,∠OAB=∠OCD.
又∵AB=CD,
∴△ABO≌△CDO(ASA),
∴OA=OC.
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEO=∠CFO=90°.
又∵∠AOE=∠COF,
∴△AOE≌△COF(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
针对训练 1.B
针对训练 2.解析:(1)如图,点E即所求.
(2)∵BF∥AE,
∴∠AEB=∠FBC,∠EAB=∠ABF.
∵BF是∠ABC的平分线,
∴∠FBC=∠ABF,
∴∠AEB=∠EAB,
∴BE=AB=4.
根据平行线分线段成比例定理可知===,
∴AF=AC=×6=.
针对训练 3.解析:(1)下图即所求.
(2)AC=RP.
理由:∵BQ=CP,∴BQ+BP=CP+BP,∴QP=BC.
由作图过程可知∠PQM=∠CBA,QR=AB,
∴△PQR≌△CBA(SAS),∴AC=RP.
例2 解析:(1)如图,连接BI,作∠DIB=∠IBC,直线ID交AC于点E,则直线DE为所求.
(2)如图,连接CI.
∵I是△ABC的内心,
∴BI平分∠ABC,CI平分∠ACB,
∴∠DBI=∠CBI,∠ECI=∠BCI.
∵DE∥BC,∴∠DIB=∠CBI,∠EIC=∠BCI,
∴∠DIB=∠DBI,∠EIC=∠ECI,
∴DB=DI,EI=EC.
设BD=x,则DI=x,CE=EI=-x.
∵DE∥BC,∴BD∶BA=CE∶CA,即x∶6=-x∶8,解得x=2,
∴AD=AB-BD=4.
∵DE∥BC,∴△ADE∽△ABC,∴DE∶BC=AD∶AB,即∶BC=4∶6,
解得BC=7,即BC的长为7.
针对训练 4.解析:分别作线段AB和线段AC的垂直平分线,交点分别为D和E,延长DE到点F,使EF=DE,连接FC,如图所示.
∵D,E分别是AB,AC的中点,
∴AD=BD,AE=CE.
在△ADE和△CFE中,
∴△ADE≌△CFE(SAS),
∴∠ADE=∠F,AD=CF,
∴CF∥AB,CF=BD,
∴四边形BCFD是平行四边形,
∴DF=BC,DF∥BC,
∴DE=DF=BC.
针对训练 5.解析:(1)如图,四边形ABCD即所作.
(2)证明:∵∠MON=90°,OM=ON,
∴∠OMN=∠ONM=45°.
由作图可得OA=OD,∠AOD=90°=∠MON,
∴∠MOA=∠NOD,
∴△OAM≌△ODN,
∴∠OND=∠OMA=45°,
∴∠AND=∠OND+∠ONM=45°+45°=90°,
∴DN⊥MN.
针对训练 6.解析:(1)如图,AE即所求.
(2)证明:∵AE平分∠BAC,
∴∠BAE=∠DAE.
∵AB=AD,AE=AE,
∴△BAE≌△DAE(SAS),
∴DE=BE.
例3 解析:(1)如图1,四边形BCEF即所求.
图1
(2)如图2,取BF的中点T,连接CT,TE,设AD交CT于点J.
图2
∵∠ACB=∠ACE=∠CAB=60°,CD=CE,
∴AB∥CE.
∵FT=CD,
∴EC=FT,
∴四边形ECTF是平行四边形,
∴EF∥CT,
∴∠DGE=∠CJD.
∵△ABC是等边三角形,
∴AC=BC,∠B=∠ACD=60°.
∵BF=2CD,BT=TF,
∴BT=CD.
在△ACD和△CBT中,
∴△ACD≌△CBT(SAS),
∴∠CAD=∠BCT,
∴∠CJD=∠CAD+∠ACJ=∠BCT+∠ACJ=60°,
∴∠DGE=∠CJD=60°.
针对训练 7.解析:(1)如图,作∠ACB的平分线CO,交AB于点O,过点O作BC的垂线,垂足为N,以点O为圆心,ON的长为半径画圆,作OM⊥AC于点M,
由作图可得BC是☉O的切线,
由角平分线的性质可得OM=ON,
∴AC是☉O的切线,
∴☉O即所求.
(2)由(1)得OM⊥AC,ON⊥BC,OM=ON.
∵∠ACB=90°,
又∵OA=1,OB=2,
∴===,
∴tanB==.
针对训练 8.解析:(1)如图1,△EDC即所求.
图1
(2)证明:如图2,连接AE,PE,设PE与AB交于点D'.
图2
∵△ABC≌△EDC,
∴AC=EC,∠ACB=∠ECD,
∴∠BCD=∠ACE.
∵AB=AC,∴∠ABC=∠ACB,AB=EC,
∴∠BAC=180°-2∠ABC.
∵CB=CD,∴∠CBD=∠CDB,
∴∠BCD=180°-2∠CBD,∴∠BAC=∠BCD,
∴∠BAC=∠ACE.
又∵AC=CA,∴△BAC≌△ECA(SAS),
∴∠ACB=∠CAE,BC=AE,∴AE∥BC,
∴∠AED'=∠P,∠EAD'=∠PBD'.
∵BP=BC,BC=AE,∴AE=BP,
∴△AD'E≌△BD'P(ASA),∴AD'=BD',
∴D'是线段AB的中点.
∵D是线段AB的中点,
∴D',D为同一个点,
∴P,D,E三点共线.
针对训练 9.解析:(1)(作法不唯一)如图1,
∴∠COQ=2∠CAQ;
点O即所求
(2)如图2,连接BC,以点B为圆心,以BC的长为半径画弧交AQ于点B1,以点B1为圆心,以任意长为半径画弧交AQ于点C1,D1,分别以点C1,D1为圆心,以大于C1D1的长为半径画弧,交于点F1,连接B1F1并延长交AP于点M.
∵AB是直径,
∴∠ACB=90°,即BC⊥AP,
根据作图可得B1C1=B1D1,C1F1=D1F1,
∴MB1⊥AQ,即∠MB1B=90°,MB1是点M到AQ的距离.
∵BC=BB1,
∴Rt△BCM≌Rt△BB1M(HL),
∴CM=B1M,
点M即所求.
(3)如图3,根据作图可得∠COQ=2∠CAQ,MC=MW=12,MW⊥AQ,连接BC,
∴在Rt△AMW中,sinA==,
∴AM===20,
∴AC=AM-CM=20-12=8.
∵AB是直径,
∴∠ACB=90°,
∴sinA==,
设BC=3x,则AB=5x,
∴在Rt△ABC中,(5x)2=(3x)2+82,
解得x=2(负值舍去),
∴BC=3x=6,
在Rt△BCM中,BM===6.
针对训练 10.解析:(1)如图,作∠ABC的平分线交AC于点D,点D即所求.
(2)∵AB=AC,∴∠ABC=∠C.
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵AD=BD,∴∠A=∠ABD,
∴∠ABC=∠C=2∠A.
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠A+2∠A=180°,∴∠A=36°.
针对训练 11.解析:(1)如图,☉O即所求.
(2)证明:如图,连接OD.
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠CAD=∠ADO,
∴AC∥OD,
∴∠ODB=∠C=90°,∴OD⊥BC.
∵OD是半径,∴BC是☉O的切线.
同课章节目录
