专题六 圆的相关证明与计算 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 专题六 圆的相关证明与计算 学案(含答案)2025年中考数学人教版一轮复习考点探究 |
|
|
| 格式 | docx | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 08:50:49 | ||
图片预览

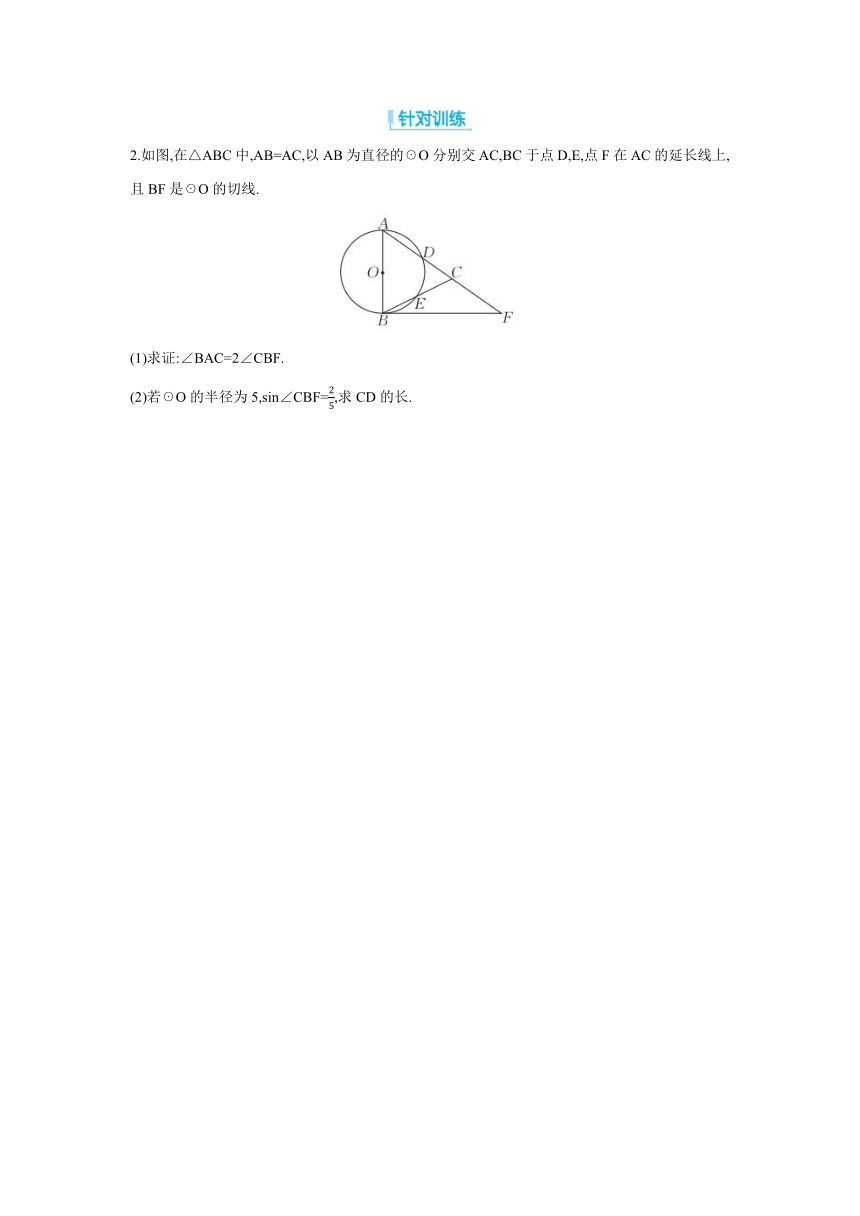



文档简介
类型一 与切线相关的证明与计算
(2024·龙岩模拟)如图,在锐角∠MON内部取一点A,过点A分别作AB⊥OM于点B,作AC⊥ON于点C,以AB为直径作☉P,CA的延长线与☉P交于点D,连接BD.
(1)求证:∠MON+∠ABD=90°.
(2)若OB=BD,点D在OP的延长线上,求证:ON是☉P的切线.
(3)当tan∠MON=1时,连接OA,若CP⊥OA于点F,求的值.
1.如图,AB是☉O的直径,P是弦AC上一动点(不与点A,C重合),过点P作PE⊥AB,垂足为E,射线EP交弧AC于点F,交过点C的切线于点D.
(1)求证:DC=DP.
(2)若∠CAB=30°,AB=4,F是弧AC的中点,求CP的长.
2.如图,在△ABC中,AB=AC,以AB为直径的☉O分别交AC,BC于点D,E,点F在AC的延长线上,且BF是☉O的切线.
(1)求证:∠BAC=2∠CBF.
(2)若☉O的半径为5,sin∠CBF=,求CD的长.
类型二 圆的综合探究
(2024·福建)如图,在△ABC中,∠BAC=90°,AB=AC,以AB为直径的☉O交BC于
点D,AE⊥OC,垂足为E,BE的延长线交于点F.
(1)求的值.
(2)求证:△AEB∽△BEC.
(3)求证:AD与EF互相平分.
3.(原创)已知△ABC内接于☉O,D是的中点,连接AD,CD,BD,AD与BC交于点P.
图1 图2
(1)如图1,若∠DBC=28°,∠ACB=74°,求∠APB和∠ABC的度数.
(2)如图2,当AB为☉O的直径时,过点D的切线与AB的延长线交于点E,若CD∥AB,求∠BDE的度数.
4.已知四边形ABCD内接于☉O,AC⊥BD,垂足为E,CF⊥AB,垂足为F,交BD于点G,连接AG.
图1 图2
(1)求证:CG=CD.
(2)如图1,若AG=4,BC=10,求☉O的半径.
(3)如图2,连接DF,交AC于点H,若∠ABD=30°,CH=6,试判断+是不是定值.若是,求出该定值;若不是,说明理由.
5.如图,AB是☉O的直径,C,D为☉O上不同于A,B的两点,并且点C,D位于直径AB的两侧,CA=CD.
图1 图2
(1)如图1,连接BD,求证:∠ABD=2∠BDC.
(2)如图2,AB,CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM.
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
6.【问题呈现】阿基米德折弦定理:阿基米德(Archimedes,公元前287-公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.如图1,AB和BC是☉O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
图2
∵M是的中点,∴MA=MC.
又∵∠A=∠C,BA=GC,
∴△MAB≌△MCG,∴MB=MG.
又∵MD⊥BC,∴BD=DG,
∴AB+BD=CG+DG,即CD=DB+BA.
【理解运用】如图1,AB、BC是☉O的两条弦,AB=4,BC=6,M是的中点,MD⊥BC于点D,则BD的长为 .
图1
【针对训练探究】如图3,若点M是的中点,【问题呈现】中的其他条件不变,判断CD、DB与BA之间存在怎样的数量关系,并加以证明.
图3
【实践应用】如图4,BC是☉O的直径,A为圆上一定点,D为圆上一动点,且满足∠DAC=45°,若AB=6,☉O的半径为5,则AD的长为 .
图4
参考答案
例1 解析:(1)证明:∵AB是☉P的直径,
∴∠ADB=90°,即AD⊥BD.
∵CD⊥ON,
∴BD∥ON,
∴∠MON=∠MBD.
∵AB⊥OM,
∴∠ABD+∠MBD=90°,
∴∠MON+∠ABD=90°.
(2)证明:如图1,连接OD,则点P在OD上,过点P作PE⊥ON于点E.
∵OB=BD,
∴∠1=∠2,
∴∠MBD=∠1+∠2=2∠1.
由(1)可知∠MON=∠MBD=2∠1,
∴OP平分∠MON.
∵PE⊥ON,PB⊥OM,
∴PE=PB,
∴ON是☉P的切线.
(3)解法一:如图2,过点P作PH⊥AD于点H,过点B作BR⊥ON于点R,
则AH=DH,∠PHC=∠CRB=90°.
设AH=x,AC=y.
由(1)得∠OCD=∠CDB=90°,
∠COB=∠BAD,
∴四边形CDBR是矩形.
∴BR=CD=
2x+y.
∵tan∠MON=1,
∴tan∠PAH=1,
∴PH=x,BD=CR=2x,OR=BR=2x+y.
∵CP⊥OA于点F,
∴∠CFO=∠PHC=90°,
∴∠3+∠5=90°.
∵AC⊥OC,
∴∠4+∠5=90°,
∴∠3=∠4,
∴△OCA∽△CHP,
∴=,即=,
∴y=2x,
∴OA===2x,
CP===x,
∴CF===x,
∴PF=x,∴=.
解法二:∵∠ACO=∠AFC=90°,
cos∠CAO==,∴AC2=AF·AO.
∵∠ABO=∠AFP=90°,
cos∠BAO==,∴AP·AB=AF·AO,
∴AC2=AP·AB.
∵AB=2AP,∴AC2=2AP2,∴AC=AP.
如图3,过点P作PH⊥AD于点H.
设PA=r,AC=r,
∵tan∠MON=1,∴∠MON=45°.
由(1)可知∠BAD=45°,在Rt△APH中,AH=PH=r,
∴CH=AC+AH=r,PC==r.
∵△CAF∽△CPH,
∴=,∴=,CF=r,
PF=CP-CF=r-r=r,
∴==.
针对训练 1.解析:
(1)证明:如图,连接OC.
∵DC切☉O于点C,∴半径OC⊥DC,∴∠DCP+∠ACO=90°.
∵PE⊥AB,
∴∠OAC+∠APE=90°.
∵∠DPC=∠APE,∴∠OAC+∠DPC=90°.
∵OA=OC,∴∠OAC=∠OCA,
∴∠DCP=∠DPC,∴CD=PD.
(2)如图,连接OF,CF.
∵∠CAB=30°,∴∠BOC=2∠CAB=60°,
∴∠AOC=120°.
∵F是的中点,∴∠FOC=∠FOA=60°.
∵OF=OC,∴△OFC是等边三角形,∴FC=OC=2.
∵∠APE=90°-∠BAC=60°,∴∠DPC=∠APE=60°.
∵DP=DC,∴△DPC是等边三角形.
∵∠CFO=∠AOF=60°,∴CF∥BE.
∵BE⊥DE,∴CF⊥DP.
∵sin∠CPF==,FC=2,∴PC=.
针对训练 2.解析:
(1)证明:如图,连接AE.
∵AB为☉O的直径,∴∠AEB=90°,∴∠BAE+∠ABE=90°.
∵AB=AC,∴∠BAE=∠CAE=∠BAC.
∵BF是☉O的切线,∴∠CBF+∠ABE=90°,
∴∠CBF=∠BAE=∠BAC,∴∠BAC=2∠CBF.
(2)如图,连接BD.
∵AB=AC=2OB=10,sin∠CBF=,
∴sin∠BAE=,∴BE=4,∴BC=2BE=8.
设CD=x,则AD=10-x.
∵AB是☉O的直径,∴∠ADB=90°,∴∠BDC=90°,
∴82-x2=102-(10-x)2,解得x=,∴CD=.
例2 解析:(1)∵AB=AC,且AB是☉O的直径,
∴AC=2AO,
∵∠BAC=90°,
在Rt△AOC 中,tan∠AOC==2.
∵AE⊥OC,
在Rt△AOE 中,tan∠AOC=,
∴=2,
∴=.
(2)证明:如图1,过点B作 BM∥AE,交EO延长线于点M,
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM.
∵=,
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
∠AEB=∠AEO+∠MEB=135°,
∠BEC=180°-∠MEB=135°,
∴∠AEB=∠BEC.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠ABM=∠CBE,
∴∠BAE=∠CBE,
∴△AEB∽△BEC.
(3)证明:如图2,连接DE,DF.
∵AB是☉O的直径,
∴∠ADB=∠AFB=90°,AB=2AO.
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°.
由(2)知,△AEB∽△BEC,
===,∠EAO=∠EBD,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°,
∴∠DEF=90°,
∴∠AFB=∠DEF,
∴AF∥DE,
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
∴四边形AEDF是平行四边形,
∴AD与EF互相平分.
针对训练 3.解析:(1)∵∠DBC=28°,∴∠CAD=28°,
∴∠APB=∠CAD+∠ACB=28°+74°=102°.
∵D是的中点,∴=,
∴∠DAB=∠CBD=28°.
在△ABP中,∠DAB=28°,∠APB=102°,
∴∠ABC=180°-∠DAB-∠APB=50°,
∴∠APB=102°,∠ABC=50°.
(2)如图,连接OD.
∵CD∥AB,
∴∠DCB=∠ABC.
∵D是的中点,
∴=,∴∠DCB=∠DBC=∠DAB.
∵AB为☉O的直径,∴∠ADB=90°,
∴∠DAB+∠ABC+∠DBC=90°,∴∠DAO=30°.
∵DE为☉O的切线,∴OD⊥DE,
∴∠BDE+∠ODB=90°.
∵∠ADO+∠ODB=90°,∴∠BDE=∠ADO.
∵OD=OA,∴∠ADO=∠DAO,
∴∠BDE=∠DAO=30°.
针对训练 4.解析:(1)证明:如图1.
图1
∵AC⊥BD,CF⊥AB,
∴∠AEB=∠AFC=90°,
∴∠2+∠BAC=90°,∠1+∠BAC=90°,
∴∠1=∠2.
∵∠1=∠3,
∴∠2=∠3.
∵∠DEC=∠GEC=90°,
∴∠3+∠CDE=90°,∠2+∠CGE=90°,
∴∠CDE=∠CGE,
∴CG=CD.
(2)如图2,连接CO并延长交☉O于点Q,连接BQ,
图2
由(1)知,CG=CD,∠2=∠3,
∴AC是DG的中垂线,
∴AG=AD.
∵AC⊥BD,
∴∠CED=90°,
∴∠CDE+∠ECD=90°.
∵CQ为☉O的直径,
∴∠CBQ=90°,
∴∠CQB+∠QCB=90°.
∵∠CQB=∠CDB,
∴∠QCB=∠3,
∴BQ=AD,
∴BQ=AD=AG=4.
在Rt△CQB中,根据勾股定理得CQ==2,
∴☉O的半径为.
(3)+的值是定值.
如图3,过点H作HM∥CD交CF于点M,
图3
∴∠CHM=∠3.
由(1)知,∠2=∠3,
∴∠CHM=∠2,
∴CM=HM.
∵HM∥CD,
∴△FMH∽△FCD,
∴==.
∵+==1,
∴+=1,
∴+=,
过点M作MN⊥CH于点N,则CN=CH=3.
在Rt△CMN中,cos∠2==.
∵∠ABD=30°,
∴∠1=∠2=∠3=30°,
∴CM==2,
∴+=.
针对训练 5.解析:(1)证明:如图1,连接OC,OD.
图1
在△OCA和△OCD中,
∴△OCA≌△OCD(SSS),
∴∠ACO=∠DCO.
∵OA=OC,
∴∠A=∠ACO.
∵∠A=∠CDB,
∴∠CDB=∠OCD,
∴OC∥DB,
∴∠ABD=∠BOC.
∵∠BOC=2∠BDC,
∴∠ABD=2∠BDC.
(2)证明:如图2,连接AD.
图2
∵MF⊥BD,
∴∠MFB=90°.
∵AB是☉O的直径,
∴∠ADB=90°,
∴∠EFB=∠ADB,
∴MF∥AD,
∴∠CME=∠CAD,∠CEM=∠CDA.
∵CA=CD,
∴∠CAD=∠CDA,
∴∠CME=∠CEM,
∴CM=CE.
(3)如图3,连接AD,BC,CO,延长CO交AD于点H,
图3
由(1)知,∠ACO=∠DCO.
∵CA=CD,
∴CH⊥AD,AH=DH.
∵∠CDB=∠CAO=∠ACH,
∴tan∠CDB=tan∠CAO=
tan∠ACH=,设BC=2a,则AC=4a,AB=2a,AH=a,CH=a,
∴OH=CH-OC=a,
∴tan∠OAH===.
∵EF∥AD,
∴∠BEF=∠OAH,
∴tan∠BEF=.
∵EB=5,
∴BF=3,EF=4.
∵tan∠EDF==,
∴DF=8,DE=4,BD=11,
∴AD=×11=,AB=×11=,
∴AE=AB-EB=.
∵∠ECB=∠EAD,∠EBC=∠EDA,
∴△ECB∽△EAD,
∴=,
∴=,
∴CE=.
针对训练 6.解析:【理解运用】由题意可得CD=DB+BA,即CD=6-CD+AB,
∴CD=6-CD+4,∴CD=5,
∴BD=BC-CD=6-5=1.
故答案为1.
【针对训练探究】DB=CD+BA.
证明:如图1,在DB上截取BG=BA,连接MA,MB,MC,MG.
图1
∵M是弧AC的中点,∴=,∴AM=MC,∠MBA=∠MBG.
∵MB=MB,∴△MAB≌△MGB(SAS),∴MA=MG,∴MC=MG.
∵DM⊥BC,∴DC=DG,∴AB+DC=BG+DG,即DB=CD+BA.
【实践应用】
如图2,当点D1在BC下方时,过点D1作D1G1⊥AC于点G1.
图2
∵BC是☉O的直径,∴∠BAC=90°.
∵AB=6,☉O的半径为5,∴AC=8.
∵∠D1AC=45°,∴CG1+AB=AG1,∴AG1=(6+8)=7,∴AD1=7.
当点D2在BC上方时,∠D2AC=45°,同理易得AD2=.
综上所述,AD的长为7或.
故答案为7或.
(2024·龙岩模拟)如图,在锐角∠MON内部取一点A,过点A分别作AB⊥OM于点B,作AC⊥ON于点C,以AB为直径作☉P,CA的延长线与☉P交于点D,连接BD.
(1)求证:∠MON+∠ABD=90°.
(2)若OB=BD,点D在OP的延长线上,求证:ON是☉P的切线.
(3)当tan∠MON=1时,连接OA,若CP⊥OA于点F,求的值.
1.如图,AB是☉O的直径,P是弦AC上一动点(不与点A,C重合),过点P作PE⊥AB,垂足为E,射线EP交弧AC于点F,交过点C的切线于点D.
(1)求证:DC=DP.
(2)若∠CAB=30°,AB=4,F是弧AC的中点,求CP的长.
2.如图,在△ABC中,AB=AC,以AB为直径的☉O分别交AC,BC于点D,E,点F在AC的延长线上,且BF是☉O的切线.
(1)求证:∠BAC=2∠CBF.
(2)若☉O的半径为5,sin∠CBF=,求CD的长.
类型二 圆的综合探究
(2024·福建)如图,在△ABC中,∠BAC=90°,AB=AC,以AB为直径的☉O交BC于
点D,AE⊥OC,垂足为E,BE的延长线交于点F.
(1)求的值.
(2)求证:△AEB∽△BEC.
(3)求证:AD与EF互相平分.
3.(原创)已知△ABC内接于☉O,D是的中点,连接AD,CD,BD,AD与BC交于点P.
图1 图2
(1)如图1,若∠DBC=28°,∠ACB=74°,求∠APB和∠ABC的度数.
(2)如图2,当AB为☉O的直径时,过点D的切线与AB的延长线交于点E,若CD∥AB,求∠BDE的度数.
4.已知四边形ABCD内接于☉O,AC⊥BD,垂足为E,CF⊥AB,垂足为F,交BD于点G,连接AG.
图1 图2
(1)求证:CG=CD.
(2)如图1,若AG=4,BC=10,求☉O的半径.
(3)如图2,连接DF,交AC于点H,若∠ABD=30°,CH=6,试判断+是不是定值.若是,求出该定值;若不是,说明理由.
5.如图,AB是☉O的直径,C,D为☉O上不同于A,B的两点,并且点C,D位于直径AB的两侧,CA=CD.
图1 图2
(1)如图1,连接BD,求证:∠ABD=2∠BDC.
(2)如图2,AB,CD交于点E,过点E作EF⊥DB于点F,延长FE交AC于点M,求证:CE=CM.
(3)在(2)的条件下,若tan∠CDB=,EB=5,求线段CE的长.
6.【问题呈现】阿基米德折弦定理:阿基米德(Archimedes,公元前287-公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.如图1,AB和BC是☉O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
图2
∵M是的中点,∴MA=MC.
又∵∠A=∠C,BA=GC,
∴△MAB≌△MCG,∴MB=MG.
又∵MD⊥BC,∴BD=DG,
∴AB+BD=CG+DG,即CD=DB+BA.
【理解运用】如图1,AB、BC是☉O的两条弦,AB=4,BC=6,M是的中点,MD⊥BC于点D,则BD的长为 .
图1
【针对训练探究】如图3,若点M是的中点,【问题呈现】中的其他条件不变,判断CD、DB与BA之间存在怎样的数量关系,并加以证明.
图3
【实践应用】如图4,BC是☉O的直径,A为圆上一定点,D为圆上一动点,且满足∠DAC=45°,若AB=6,☉O的半径为5,则AD的长为 .
图4
参考答案
例1 解析:(1)证明:∵AB是☉P的直径,
∴∠ADB=90°,即AD⊥BD.
∵CD⊥ON,
∴BD∥ON,
∴∠MON=∠MBD.
∵AB⊥OM,
∴∠ABD+∠MBD=90°,
∴∠MON+∠ABD=90°.
(2)证明:如图1,连接OD,则点P在OD上,过点P作PE⊥ON于点E.
∵OB=BD,
∴∠1=∠2,
∴∠MBD=∠1+∠2=2∠1.
由(1)可知∠MON=∠MBD=2∠1,
∴OP平分∠MON.
∵PE⊥ON,PB⊥OM,
∴PE=PB,
∴ON是☉P的切线.
(3)解法一:如图2,过点P作PH⊥AD于点H,过点B作BR⊥ON于点R,
则AH=DH,∠PHC=∠CRB=90°.
设AH=x,AC=y.
由(1)得∠OCD=∠CDB=90°,
∠COB=∠BAD,
∴四边形CDBR是矩形.
∴BR=CD=
2x+y.
∵tan∠MON=1,
∴tan∠PAH=1,
∴PH=x,BD=CR=2x,OR=BR=2x+y.
∵CP⊥OA于点F,
∴∠CFO=∠PHC=90°,
∴∠3+∠5=90°.
∵AC⊥OC,
∴∠4+∠5=90°,
∴∠3=∠4,
∴△OCA∽△CHP,
∴=,即=,
∴y=2x,
∴OA===2x,
CP===x,
∴CF===x,
∴PF=x,∴=.
解法二:∵∠ACO=∠AFC=90°,
cos∠CAO==,∴AC2=AF·AO.
∵∠ABO=∠AFP=90°,
cos∠BAO==,∴AP·AB=AF·AO,
∴AC2=AP·AB.
∵AB=2AP,∴AC2=2AP2,∴AC=AP.
如图3,过点P作PH⊥AD于点H.
设PA=r,AC=r,
∵tan∠MON=1,∴∠MON=45°.
由(1)可知∠BAD=45°,在Rt△APH中,AH=PH=r,
∴CH=AC+AH=r,PC==r.
∵△CAF∽△CPH,
∴=,∴=,CF=r,
PF=CP-CF=r-r=r,
∴==.
针对训练 1.解析:
(1)证明:如图,连接OC.
∵DC切☉O于点C,∴半径OC⊥DC,∴∠DCP+∠ACO=90°.
∵PE⊥AB,
∴∠OAC+∠APE=90°.
∵∠DPC=∠APE,∴∠OAC+∠DPC=90°.
∵OA=OC,∴∠OAC=∠OCA,
∴∠DCP=∠DPC,∴CD=PD.
(2)如图,连接OF,CF.
∵∠CAB=30°,∴∠BOC=2∠CAB=60°,
∴∠AOC=120°.
∵F是的中点,∴∠FOC=∠FOA=60°.
∵OF=OC,∴△OFC是等边三角形,∴FC=OC=2.
∵∠APE=90°-∠BAC=60°,∴∠DPC=∠APE=60°.
∵DP=DC,∴△DPC是等边三角形.
∵∠CFO=∠AOF=60°,∴CF∥BE.
∵BE⊥DE,∴CF⊥DP.
∵sin∠CPF==,FC=2,∴PC=.
针对训练 2.解析:
(1)证明:如图,连接AE.
∵AB为☉O的直径,∴∠AEB=90°,∴∠BAE+∠ABE=90°.
∵AB=AC,∴∠BAE=∠CAE=∠BAC.
∵BF是☉O的切线,∴∠CBF+∠ABE=90°,
∴∠CBF=∠BAE=∠BAC,∴∠BAC=2∠CBF.
(2)如图,连接BD.
∵AB=AC=2OB=10,sin∠CBF=,
∴sin∠BAE=,∴BE=4,∴BC=2BE=8.
设CD=x,则AD=10-x.
∵AB是☉O的直径,∴∠ADB=90°,∴∠BDC=90°,
∴82-x2=102-(10-x)2,解得x=,∴CD=.
例2 解析:(1)∵AB=AC,且AB是☉O的直径,
∴AC=2AO,
∵∠BAC=90°,
在Rt△AOC 中,tan∠AOC==2.
∵AE⊥OC,
在Rt△AOE 中,tan∠AOC=,
∴=2,
∴=.
(2)证明:如图1,过点B作 BM∥AE,交EO延长线于点M,
∴∠BAE=∠ABM,∠AEO=∠BMO=90°.
∵AO=BO,
∴△AOE≌△BOM(AAS),
∴AE=BM,OE=OM.
∵=,
∴BM=2OE=EM,
∴∠MEB=∠MBE=45°,
∠AEB=∠AEO+∠MEB=135°,
∠BEC=180°-∠MEB=135°,
∴∠AEB=∠BEC.
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∴∠ABM=∠CBE,
∴∠BAE=∠CBE,
∴△AEB∽△BEC.
(3)证明:如图2,连接DE,DF.
∵AB是☉O的直径,
∴∠ADB=∠AFB=90°,AB=2AO.
∵AB=AC,∠BAC=90°,
∴BC=2BD,∠DAB=45°.
由(2)知,△AEB∽△BEC,
===,∠EAO=∠EBD,
∴△AOE∽△BDE,
∴∠BED=∠AEO=90°,
∴∠DEF=90°,
∴∠AFB=∠DEF,
∴AF∥DE,
由(2)知,∠AEB=135°,
∴∠AEF=180°-∠AEB=45°.
∵∠DFB=∠DAB=45°,
∴∠DFB=∠AEF,
∴AE∥FD,
∴四边形AEDF是平行四边形,
∴AD与EF互相平分.
针对训练 3.解析:(1)∵∠DBC=28°,∴∠CAD=28°,
∴∠APB=∠CAD+∠ACB=28°+74°=102°.
∵D是的中点,∴=,
∴∠DAB=∠CBD=28°.
在△ABP中,∠DAB=28°,∠APB=102°,
∴∠ABC=180°-∠DAB-∠APB=50°,
∴∠APB=102°,∠ABC=50°.
(2)如图,连接OD.
∵CD∥AB,
∴∠DCB=∠ABC.
∵D是的中点,
∴=,∴∠DCB=∠DBC=∠DAB.
∵AB为☉O的直径,∴∠ADB=90°,
∴∠DAB+∠ABC+∠DBC=90°,∴∠DAO=30°.
∵DE为☉O的切线,∴OD⊥DE,
∴∠BDE+∠ODB=90°.
∵∠ADO+∠ODB=90°,∴∠BDE=∠ADO.
∵OD=OA,∴∠ADO=∠DAO,
∴∠BDE=∠DAO=30°.
针对训练 4.解析:(1)证明:如图1.
图1
∵AC⊥BD,CF⊥AB,
∴∠AEB=∠AFC=90°,
∴∠2+∠BAC=90°,∠1+∠BAC=90°,
∴∠1=∠2.
∵∠1=∠3,
∴∠2=∠3.
∵∠DEC=∠GEC=90°,
∴∠3+∠CDE=90°,∠2+∠CGE=90°,
∴∠CDE=∠CGE,
∴CG=CD.
(2)如图2,连接CO并延长交☉O于点Q,连接BQ,
图2
由(1)知,CG=CD,∠2=∠3,
∴AC是DG的中垂线,
∴AG=AD.
∵AC⊥BD,
∴∠CED=90°,
∴∠CDE+∠ECD=90°.
∵CQ为☉O的直径,
∴∠CBQ=90°,
∴∠CQB+∠QCB=90°.
∵∠CQB=∠CDB,
∴∠QCB=∠3,
∴BQ=AD,
∴BQ=AD=AG=4.
在Rt△CQB中,根据勾股定理得CQ==2,
∴☉O的半径为.
(3)+的值是定值.
如图3,过点H作HM∥CD交CF于点M,
图3
∴∠CHM=∠3.
由(1)知,∠2=∠3,
∴∠CHM=∠2,
∴CM=HM.
∵HM∥CD,
∴△FMH∽△FCD,
∴==.
∵+==1,
∴+=1,
∴+=,
过点M作MN⊥CH于点N,则CN=CH=3.
在Rt△CMN中,cos∠2==.
∵∠ABD=30°,
∴∠1=∠2=∠3=30°,
∴CM==2,
∴+=.
针对训练 5.解析:(1)证明:如图1,连接OC,OD.
图1
在△OCA和△OCD中,
∴△OCA≌△OCD(SSS),
∴∠ACO=∠DCO.
∵OA=OC,
∴∠A=∠ACO.
∵∠A=∠CDB,
∴∠CDB=∠OCD,
∴OC∥DB,
∴∠ABD=∠BOC.
∵∠BOC=2∠BDC,
∴∠ABD=2∠BDC.
(2)证明:如图2,连接AD.
图2
∵MF⊥BD,
∴∠MFB=90°.
∵AB是☉O的直径,
∴∠ADB=90°,
∴∠EFB=∠ADB,
∴MF∥AD,
∴∠CME=∠CAD,∠CEM=∠CDA.
∵CA=CD,
∴∠CAD=∠CDA,
∴∠CME=∠CEM,
∴CM=CE.
(3)如图3,连接AD,BC,CO,延长CO交AD于点H,
图3
由(1)知,∠ACO=∠DCO.
∵CA=CD,
∴CH⊥AD,AH=DH.
∵∠CDB=∠CAO=∠ACH,
∴tan∠CDB=tan∠CAO=
tan∠ACH=,设BC=2a,则AC=4a,AB=2a,AH=a,CH=a,
∴OH=CH-OC=a,
∴tan∠OAH===.
∵EF∥AD,
∴∠BEF=∠OAH,
∴tan∠BEF=.
∵EB=5,
∴BF=3,EF=4.
∵tan∠EDF==,
∴DF=8,DE=4,BD=11,
∴AD=×11=,AB=×11=,
∴AE=AB-EB=.
∵∠ECB=∠EAD,∠EBC=∠EDA,
∴△ECB∽△EAD,
∴=,
∴=,
∴CE=.
针对训练 6.解析:【理解运用】由题意可得CD=DB+BA,即CD=6-CD+AB,
∴CD=6-CD+4,∴CD=5,
∴BD=BC-CD=6-5=1.
故答案为1.
【针对训练探究】DB=CD+BA.
证明:如图1,在DB上截取BG=BA,连接MA,MB,MC,MG.
图1
∵M是弧AC的中点,∴=,∴AM=MC,∠MBA=∠MBG.
∵MB=MB,∴△MAB≌△MGB(SAS),∴MA=MG,∴MC=MG.
∵DM⊥BC,∴DC=DG,∴AB+DC=BG+DG,即DB=CD+BA.
【实践应用】
如图2,当点D1在BC下方时,过点D1作D1G1⊥AC于点G1.
图2
∵BC是☉O的直径,∴∠BAC=90°.
∵AB=6,☉O的半径为5,∴AC=8.
∵∠D1AC=45°,∴CG1+AB=AG1,∴AG1=(6+8)=7,∴AD1=7.
当点D2在BC上方时,∠D2AC=45°,同理易得AD2=.
综上所述,AD的长为7或.
故答案为7或.
同课章节目录
