专题五 综合与实践(2024年新增题型) 学案(含答案)2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 专题五 综合与实践(2024年新增题型) 学案(含答案)2025年中考数学人教版一轮复习考点探究 |
|
|
| 格式 | docx | ||
| 文件大小 | 323.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览

文档简介
专题五 综合与实践(2024年新增题型)
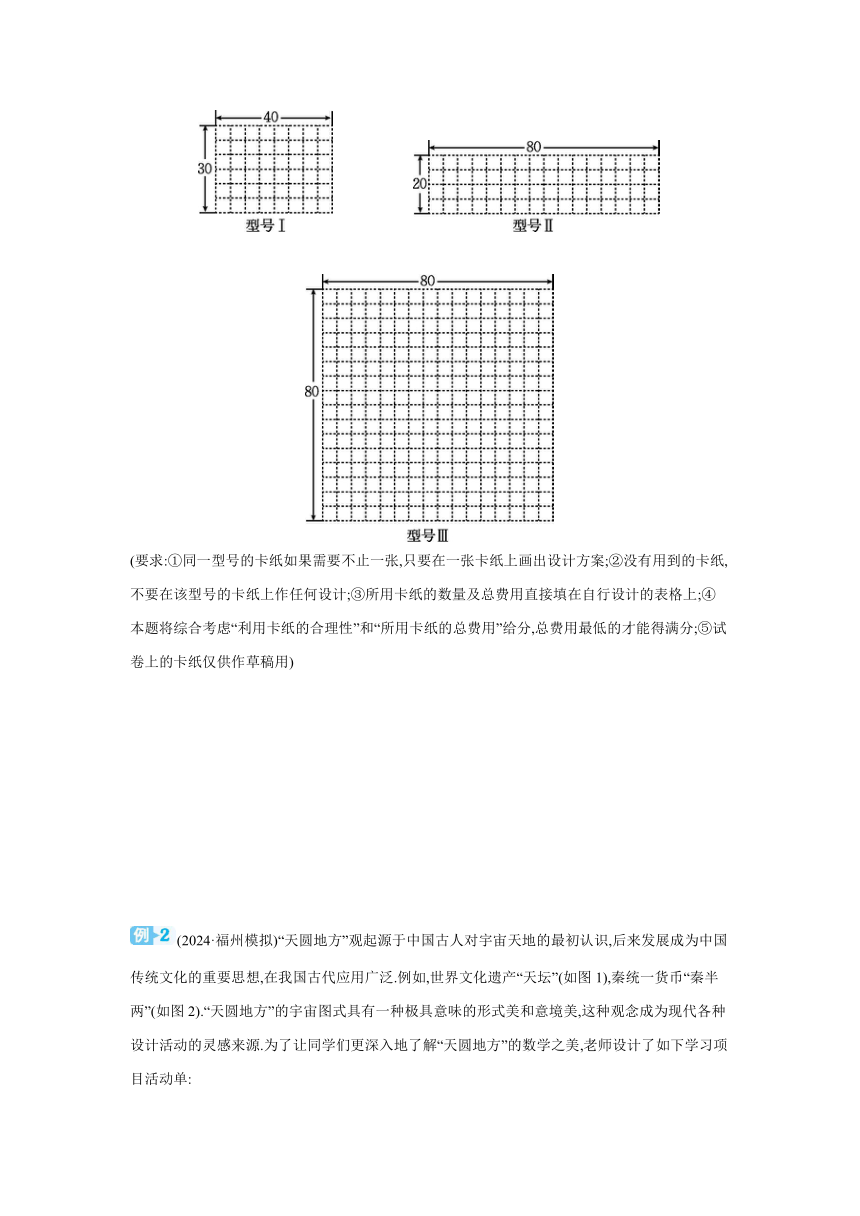
(2024·福建)在手工制作课上,老师提供了如图1所示的矩形卡纸ABCD,要求大家利用它制作一个底面为正方形的礼品盒.小明按照如图2所示的方式裁剪(其中AE=FB),恰好得到纸盒的展开图,并利用该展开图折成一个礼品盒,如图3所示.
(1)直接写出的值.
(2)如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”,如图4所示,那么应选择的纸盒展开图图样是( )
(3)今有三种不同型号的矩形卡纸,其规格、单价如下表所示:
卡纸型号 型号Ⅰ 型号Ⅱ 型号Ⅲ
规格/cm 30×40 20×80 80×80
单价/元 3 5 20
现以小明设计的纸盒展开图(图2)为基本样式,适当调整AE,EF的比例,制作棱长为10cm的正方体礼品盒.如果要制作27个这样的礼品盒,请你合理选择上述卡纸(包括卡纸的型号及相应型号卡纸的张数),并在卡纸上画出设计示意图(包括一张卡纸可制作几个礼品盒,其展开图在卡纸上的分布情况),给出所用卡纸的总费用.
(要求:①同一型号的卡纸如果需要不止一张,只要在一张卡纸上画出设计方案;②没有用到的卡纸,不要在该型号的卡纸上作任何设计;③所用卡纸的数量及总费用直接填在自行设计的表格上;④本题将综合考虑“利用卡纸的合理性”和“所用卡纸的总费用”给分,总费用最低的才能得满分;⑤试卷上的卡纸仅供作草稿用)
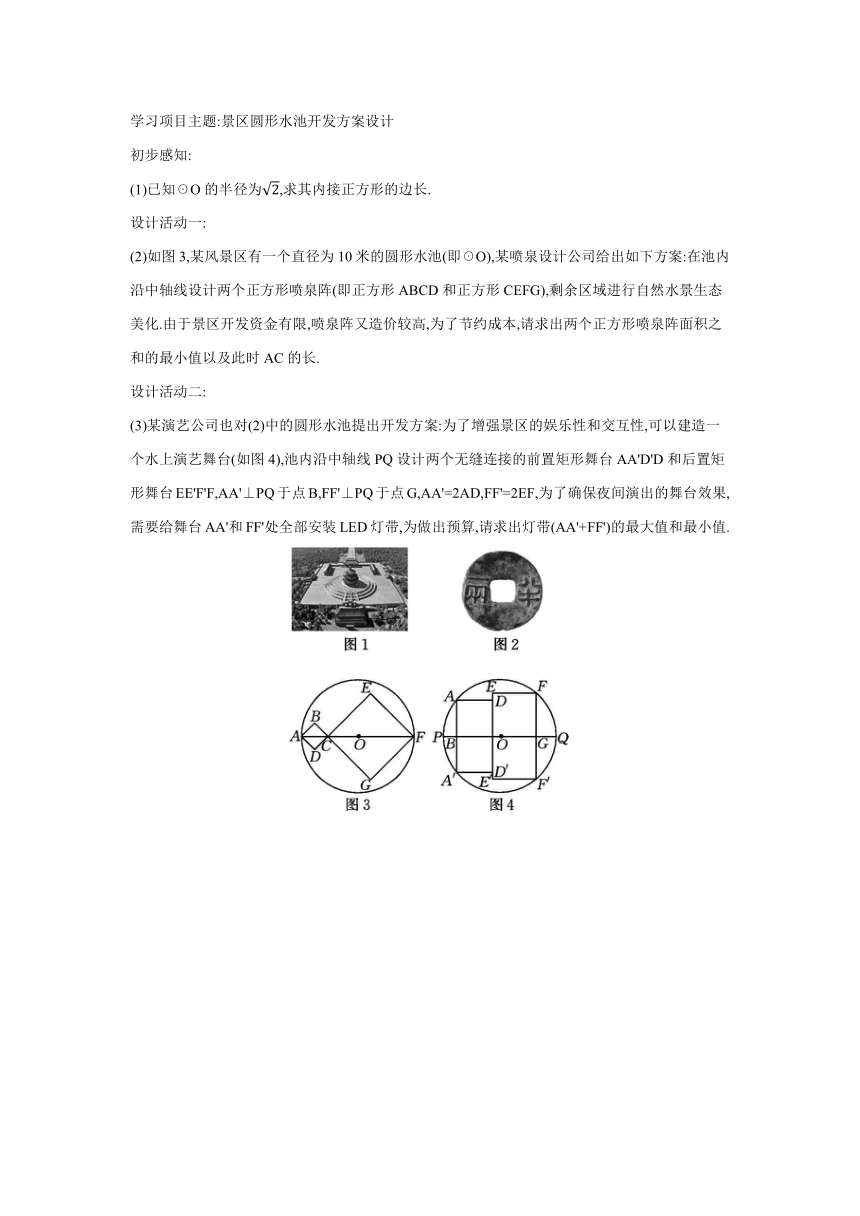
(2024·福州模拟)“天圆地方”观起源于中国古人对宇宙天地的最初认识,后来发展成为中国传统文化的重要思想,在我国古代应用广泛.例如,世界文化遗产“天坛”(如图1),秦统一货币“秦半两”(如图2).“天圆地方”的宇宙图式具有一种极具意味的形式美和意境美,这种观念成为现代各种设计活动的灵感来源.为了让同学们更深入地了解“天圆地方”的数学之美,老师设计了如下学习项目活动单:
学习项目主题:景区圆形水池开发方案设计
初步感知:
(1)已知☉O的半径为,求其内接正方形的边长.
设计活动一:
(2)如图3,某风景区有一个直径为10米的圆形水池(即☉O),某喷泉设计公司给出如下方案:在池内沿中轴线设计两个正方形喷泉阵(即正方形ABCD和正方形CEFG),剩余区域进行自然水景生态美化.由于景区开发资金有限,喷泉阵又造价较高,为了节约成本,请求出两个正方形喷泉阵面积之和的最小值以及此时AC的长.
设计活动二:
(3)某演艺公司也对(2)中的圆形水池提出开发方案:为了增强景区的娱乐性和交互性,可以建造一个水上演艺舞台(如图4),池内沿中轴线PQ设计两个无缝连接的前置矩形舞台AA'D'D和后置矩形舞台EE'F'F,AA'⊥PQ于点B,FF'⊥PQ于点G,AA'=2AD,FF'=2EF,为了确保夜间演出的舞台效果,需要给舞台AA'和FF'处全部安装LED灯带,为做出预算,请求出灯带(AA'+FF')的最大值和最小值.
参考答案
例1 解析:(1)2.
提示:如图1,
上述图形折叠后变成图2,
由折叠和题意可知,GH=AE+FB,AH=DH,
∵四边形EFNM是正方形,∴EM=EF,即 AG=EF,
∴GH+AG=AE+FB+EF,即AH=AB.
∵AH=DH,
∴==2,
∴的值为2.
(2)C.
提示:根据几何体的展开图可知,“吉”和“如”在相对的面上,“祥”和“意”在相对的面上,而相对的面上的字中间相隔一个几何图形,且字体相反,
∴C选项符合题意.
(3)需要卡纸型号的数量及总费用如下表所示.理由如下:
卡纸型号 型号Ⅰ 型号Ⅱ 型号Ⅲ
需要卡纸的数量/张 1 3 2
需要卡纸的总费用/元 58
根据(1)和题意可得卡纸每格的边长为5cm,如图3,则要制作一个边长为10cm的正方体的展开图如下:
∴每张型号Ⅲ卡纸可制作10个正方体,如图4:
每张型号Ⅱ卡纸可制作2个正方体,如图5:
每张型号Ⅰ卡纸可制作1个正方体,如图6:
∴可选择型号Ⅲ卡纸2张,型号Ⅱ卡纸3张,型号Ⅰ卡纸1张,则10×2+2×3+1×1=27(个),
∴所用卡纸总费用为20×2+5×3+3×1=58(元).
说明:本参考答案仅给出一种解法供参考.
例2 解析:(1)如图1,连接AC.
∵四边形ABCD是☉O的内接正方形,
∴AC是直径.
∵☉O的半径为,即AC=2,
∴AB=CB=2.
(2)设AC=x米,则CF=(10-x)米,
设两个正方形喷泉阵的面积和为y平方米,
则y=x2+(10-x)2=x2-10x+50=(x-5)2+25.
∵1>0,∴当x=5时,y有最小值,最小值为25,
∴两个正方形的面积和的最小值为25平方米,此时AC的长为5米.
(3)如图2,设PQ交EE'于点C,连接AC,CF'.设AD=a米.EF=b米.
∵PQ是直径,PQ⊥AA',PQ⊥FF',∴AB=A'B,FG=F'G.
∵AA'=2AD,FF'=2EF,
∴AB=A'B=AD=a米,FG=F'G=FE=b米.
又∵∠BAD=∠ADC=∠ABC=90°,
∴四边形ABCD是正方形.
同理可证四边形A'BCD',四边形CGF'E',四边形CEFG都是正方形,
∴∠ACB=∠GCF'=45°,
∴A,C,F'共线,
∴AC=a米,CF'=b米,
∴AF'=(a+b)米.
∵AA'+FF'=2(a+b)米,
∴当AF'的值最大时,AA'+FF'的值最大,当AF'的值最小时,AA'+FF'的值最小.
∵当AF'是直径时,AF'的值最大,此时 (a+b)=10,
∴a+b=5,
∴AA'+FF'的最大值为10 米.
如图3,当点E落在☉O上时,AF'的值最小,连接AO,OF,AF',此时OC=OG.
在Rt△OFG中,OF=5米.FG=CG=2OG,
∴OG=OC=米,FG=2米.
设AB=BC=m米,则m2+(m+)2=52,
解得m=(负根已经舍去),
∴AA'+FF'=2AB+2FG=2+4=6米,
∴AA'+FF'的最小值为6米.
(2024·福建)在手工制作课上,老师提供了如图1所示的矩形卡纸ABCD,要求大家利用它制作一个底面为正方形的礼品盒.小明按照如图2所示的方式裁剪(其中AE=FB),恰好得到纸盒的展开图,并利用该展开图折成一个礼品盒,如图3所示.
(1)直接写出的值.
(2)如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”,如图4所示,那么应选择的纸盒展开图图样是( )
(3)今有三种不同型号的矩形卡纸,其规格、单价如下表所示:
卡纸型号 型号Ⅰ 型号Ⅱ 型号Ⅲ
规格/cm 30×40 20×80 80×80
单价/元 3 5 20
现以小明设计的纸盒展开图(图2)为基本样式,适当调整AE,EF的比例,制作棱长为10cm的正方体礼品盒.如果要制作27个这样的礼品盒,请你合理选择上述卡纸(包括卡纸的型号及相应型号卡纸的张数),并在卡纸上画出设计示意图(包括一张卡纸可制作几个礼品盒,其展开图在卡纸上的分布情况),给出所用卡纸的总费用.
(要求:①同一型号的卡纸如果需要不止一张,只要在一张卡纸上画出设计方案;②没有用到的卡纸,不要在该型号的卡纸上作任何设计;③所用卡纸的数量及总费用直接填在自行设计的表格上;④本题将综合考虑“利用卡纸的合理性”和“所用卡纸的总费用”给分,总费用最低的才能得满分;⑤试卷上的卡纸仅供作草稿用)
(2024·福州模拟)“天圆地方”观起源于中国古人对宇宙天地的最初认识,后来发展成为中国传统文化的重要思想,在我国古代应用广泛.例如,世界文化遗产“天坛”(如图1),秦统一货币“秦半两”(如图2).“天圆地方”的宇宙图式具有一种极具意味的形式美和意境美,这种观念成为现代各种设计活动的灵感来源.为了让同学们更深入地了解“天圆地方”的数学之美,老师设计了如下学习项目活动单:
学习项目主题:景区圆形水池开发方案设计
初步感知:
(1)已知☉O的半径为,求其内接正方形的边长.
设计活动一:
(2)如图3,某风景区有一个直径为10米的圆形水池(即☉O),某喷泉设计公司给出如下方案:在池内沿中轴线设计两个正方形喷泉阵(即正方形ABCD和正方形CEFG),剩余区域进行自然水景生态美化.由于景区开发资金有限,喷泉阵又造价较高,为了节约成本,请求出两个正方形喷泉阵面积之和的最小值以及此时AC的长.
设计活动二:
(3)某演艺公司也对(2)中的圆形水池提出开发方案:为了增强景区的娱乐性和交互性,可以建造一个水上演艺舞台(如图4),池内沿中轴线PQ设计两个无缝连接的前置矩形舞台AA'D'D和后置矩形舞台EE'F'F,AA'⊥PQ于点B,FF'⊥PQ于点G,AA'=2AD,FF'=2EF,为了确保夜间演出的舞台效果,需要给舞台AA'和FF'处全部安装LED灯带,为做出预算,请求出灯带(AA'+FF')的最大值和最小值.
参考答案
例1 解析:(1)2.
提示:如图1,
上述图形折叠后变成图2,
由折叠和题意可知,GH=AE+FB,AH=DH,
∵四边形EFNM是正方形,∴EM=EF,即 AG=EF,
∴GH+AG=AE+FB+EF,即AH=AB.
∵AH=DH,
∴==2,
∴的值为2.
(2)C.
提示:根据几何体的展开图可知,“吉”和“如”在相对的面上,“祥”和“意”在相对的面上,而相对的面上的字中间相隔一个几何图形,且字体相反,
∴C选项符合题意.
(3)需要卡纸型号的数量及总费用如下表所示.理由如下:
卡纸型号 型号Ⅰ 型号Ⅱ 型号Ⅲ
需要卡纸的数量/张 1 3 2
需要卡纸的总费用/元 58
根据(1)和题意可得卡纸每格的边长为5cm,如图3,则要制作一个边长为10cm的正方体的展开图如下:
∴每张型号Ⅲ卡纸可制作10个正方体,如图4:
每张型号Ⅱ卡纸可制作2个正方体,如图5:
每张型号Ⅰ卡纸可制作1个正方体,如图6:
∴可选择型号Ⅲ卡纸2张,型号Ⅱ卡纸3张,型号Ⅰ卡纸1张,则10×2+2×3+1×1=27(个),
∴所用卡纸总费用为20×2+5×3+3×1=58(元).
说明:本参考答案仅给出一种解法供参考.
例2 解析:(1)如图1,连接AC.
∵四边形ABCD是☉O的内接正方形,
∴AC是直径.
∵☉O的半径为,即AC=2,
∴AB=CB=2.
(2)设AC=x米,则CF=(10-x)米,
设两个正方形喷泉阵的面积和为y平方米,
则y=x2+(10-x)2=x2-10x+50=(x-5)2+25.
∵1>0,∴当x=5时,y有最小值,最小值为25,
∴两个正方形的面积和的最小值为25平方米,此时AC的长为5米.
(3)如图2,设PQ交EE'于点C,连接AC,CF'.设AD=a米.EF=b米.
∵PQ是直径,PQ⊥AA',PQ⊥FF',∴AB=A'B,FG=F'G.
∵AA'=2AD,FF'=2EF,
∴AB=A'B=AD=a米,FG=F'G=FE=b米.
又∵∠BAD=∠ADC=∠ABC=90°,
∴四边形ABCD是正方形.
同理可证四边形A'BCD',四边形CGF'E',四边形CEFG都是正方形,
∴∠ACB=∠GCF'=45°,
∴A,C,F'共线,
∴AC=a米,CF'=b米,
∴AF'=(a+b)米.
∵AA'+FF'=2(a+b)米,
∴当AF'的值最大时,AA'+FF'的值最大,当AF'的值最小时,AA'+FF'的值最小.
∵当AF'是直径时,AF'的值最大,此时 (a+b)=10,
∴a+b=5,
∴AA'+FF'的最大值为10 米.
如图3,当点E落在☉O上时,AF'的值最小,连接AO,OF,AF',此时OC=OG.
在Rt△OFG中,OF=5米.FG=CG=2OG,
∴OG=OC=米,FG=2米.
设AB=BC=m米,则m2+(m+)2=52,
解得m=(负根已经舍去),
∴AA'+FF'=2AB+2FG=2+4=6米,
∴AA'+FF'的最小值为6米.
同课章节目录
