专题一 跨学科融合 学案(含答案) 2025年中考数学人教版一轮复习考点探究
文档属性
| 名称 | 专题一 跨学科融合 学案(含答案) 2025年中考数学人教版一轮复习考点探究 | 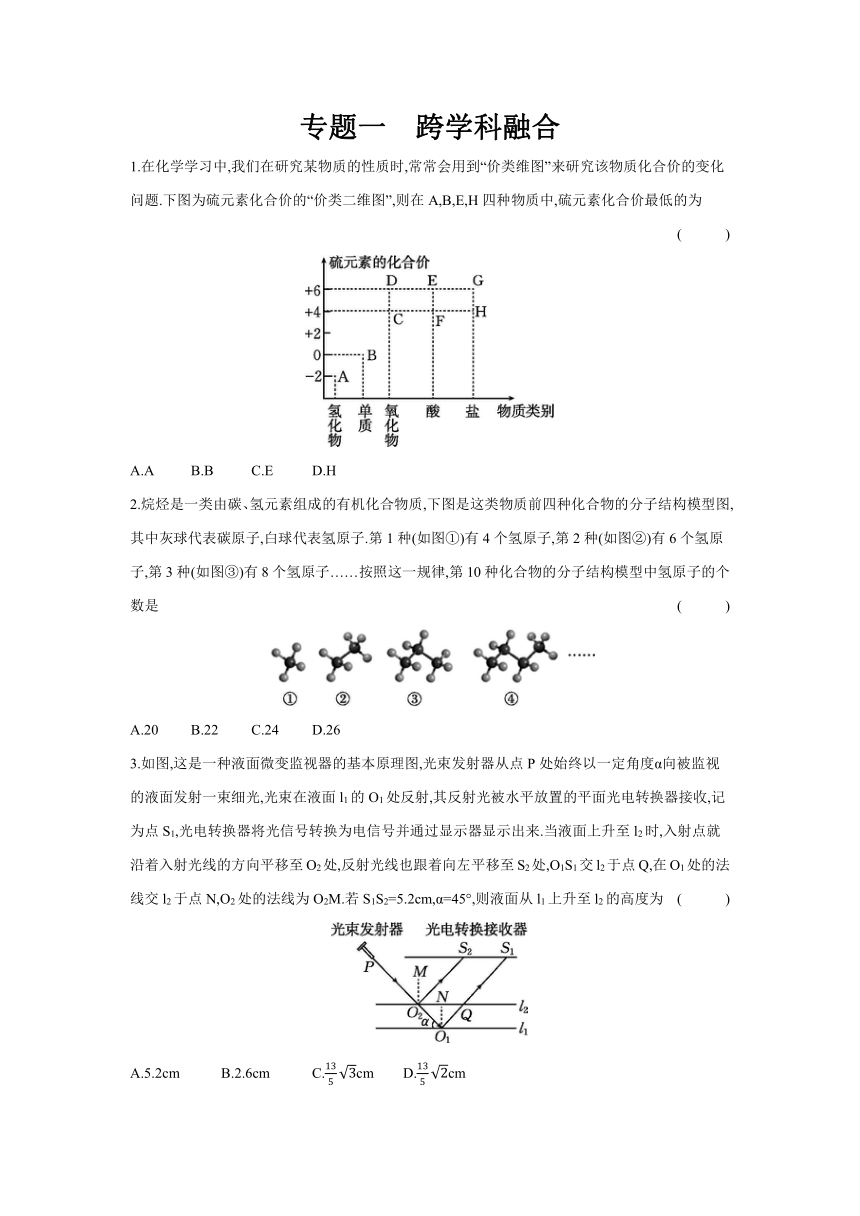 | |
| 格式 | docx | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 08:54:55 | ||
图片预览


文档简介
专题一 跨学科融合
1.在化学学习中,我们在研究某物质的性质时,常常会用到“价类维图”来研究该物质化合价的变化问题.下图为硫元素化合价的“价类二维图”,则在A,B,E,H四种物质中,硫元素化合价最低的为 ( )
A.A B.B C.E D.H
2.烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种(如图①)有4个氢原子,第2种(如图②)有6个氢原子,第3种(如图③)有8个氢原子……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是 ( )
A.20 B.22 C.24 D.26
3.如图,这是一种液面微变监视器的基本原理图,光束发射器从点P处始终以一定角度α向被监视的液面发射一束细光,光束在液面l1的O1处反射,其反射光被水平放置的平面光电转换器接收,记为点S1,光电转换器将光信号转换为电信号并通过显示器显示出来.当液面上升至l2时,入射点就沿着入射光线的方向平移至O2处,反射光线也跟着向左平移至S2处,O1S1交l2于点Q,在O1处的法线交l2于点N,O2处的法线为O2M.若S1S2=5.2cm,α=45°,则液面从l1上升至l2的高度为 ( )
A.5.2cm B.2.6cm C.cm D.cm
4.铁的密度约为7.9kg/cm3,铁的质量m(单位:kg)与体积V(单位:cm3)成正比例.一个体积为10cm3的铁块,它的质量为 kg.
5.如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3.当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 .
6.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A'B'.设AB=36cm,A'B'=24cm.小孔O到AB的距离为30cm,则小孔O到A'B'的距离为 cm.
7.(2024·漳州一模)如图,用2个电子元件①②组成一个电路系统,有两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作,系统正常工作的概率称为该系统的可靠性.这2个电子元件中,每个元件正常工作分别记为R1,R2,每个元件正常工作的概率均为,每个元件不能正常工作分别记为,,且能否正常工作互相不影响.当某元件不能正常工作时,该元件在电路中将形成断路.
(1)请列出方案1中从A到B的电路的所有情况,并求出该电路为断路的概率.
(2)根据电路系统正常工作的概率,说明哪种连接方案更稳定可靠.
8.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值叫作介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为α,折射角为β,且cosα=,β=30°,求该介质的折射率.
(2)现有一块与(1)中折射率相同的长方体介质如图1所示,A,B,C,D分别是长方体棱的中点,若光线经真空从矩形A1D1D2A2的对角线交点O处射入,其折射光线恰好从点C处射出.如图2,已知α=60°,CD=10 cm,求截面ABCD的面积.
参考答案
1.A 2.B 3.B 4.79 5.220 6.20
7.解析:(1)方案1所有情况如下表:
R2
R1 (R1,R2) (R1,)
(,R2) (,)
从A到B的电路共4种等可能的结果,其中该电路为断路的有3种,
∴该电路为断路的概率为.
(2)方案2更稳定可靠.理由如下:
由(1)得方案1中电路系统正常工作的概率为1-=;
方案2中从A到B的电路的所有可能结果为(R1,R2),(R1,),(,R2),(,),共4种等可能的结果,其中电路系统正常工作有3种,∴方案2中电路系统正常工作的概率为.
∵ <,
∴方案2更稳定可靠.
8.解析:(1)如图,∵cosα=,
∴设b=x,则c=4x,由勾股定理得a==3x,
∴sinα===.
又∵β=30°,
∴sinβ=sin30°=,
∴折射率为==.
(2)根据折射率与(1)的材料相同,可得折射率为.
∵α=60°,
∴==,
∴sinβ=.
∵四边形ABCD是矩形,O是AD的中点,
∴AD=2OD,∠ADC=90°.
又∵∠OCD=β,
∴sin∠OCD=sinβ=.
在Rt△ODC中,设OD=x,OC=3x,
由勾股定理得CD==x,
∴tanβ===.
又∵CD=10cm,
∴=,
∴OD=5cm,
∴AD=10cm,
∴截面ABCD的面积为10×10=100cm2.
1.在化学学习中,我们在研究某物质的性质时,常常会用到“价类维图”来研究该物质化合价的变化问题.下图为硫元素化合价的“价类二维图”,则在A,B,E,H四种物质中,硫元素化合价最低的为 ( )
A.A B.B C.E D.H
2.烷烃是一类由碳、氢元素组成的有机化合物质,下图是这类物质前四种化合物的分子结构模型图,其中灰球代表碳原子,白球代表氢原子.第1种(如图①)有4个氢原子,第2种(如图②)有6个氢原子,第3种(如图③)有8个氢原子……按照这一规律,第10种化合物的分子结构模型中氢原子的个数是 ( )
A.20 B.22 C.24 D.26
3.如图,这是一种液面微变监视器的基本原理图,光束发射器从点P处始终以一定角度α向被监视的液面发射一束细光,光束在液面l1的O1处反射,其反射光被水平放置的平面光电转换器接收,记为点S1,光电转换器将光信号转换为电信号并通过显示器显示出来.当液面上升至l2时,入射点就沿着入射光线的方向平移至O2处,反射光线也跟着向左平移至S2处,O1S1交l2于点Q,在O1处的法线交l2于点N,O2处的法线为O2M.若S1S2=5.2cm,α=45°,则液面从l1上升至l2的高度为 ( )
A.5.2cm B.2.6cm C.cm D.cm
4.铁的密度约为7.9kg/cm3,铁的质量m(单位:kg)与体积V(单位:cm3)成正比例.一个体积为10cm3的铁块,它的质量为 kg.
5.如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3.当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为 .
6.物理课上学过小孔成像的原理,它是一种利用光的直线传播特性实现图像投影的方法.如图,燃烧的蜡烛(竖直放置)AB经小孔O在屏幕(竖直放置)上成像A'B'.设AB=36cm,A'B'=24cm.小孔O到AB的距离为30cm,则小孔O到A'B'的距离为 cm.
7.(2024·漳州一模)如图,用2个电子元件①②组成一个电路系统,有两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作,系统正常工作的概率称为该系统的可靠性.这2个电子元件中,每个元件正常工作分别记为R1,R2,每个元件正常工作的概率均为,每个元件不能正常工作分别记为,,且能否正常工作互相不影响.当某元件不能正常工作时,该元件在电路中将形成断路.
(1)请列出方案1中从A到B的电路的所有情况,并求出该电路为断路的概率.
(2)根据电路系统正常工作的概率,说明哪种连接方案更稳定可靠.
8.小明从科普读物中了解到,光从真空射入介质发生折射时,入射角α的正弦值与折射角β的正弦值的比值叫作介质的“绝对折射率”,简称“折射率”.它表示光在介质中传播时,介质对光作用的一种特征.
(1)若光从真空射入某介质,入射角为α,折射角为β,且cosα=,β=30°,求该介质的折射率.
(2)现有一块与(1)中折射率相同的长方体介质如图1所示,A,B,C,D分别是长方体棱的中点,若光线经真空从矩形A1D1D2A2的对角线交点O处射入,其折射光线恰好从点C处射出.如图2,已知α=60°,CD=10 cm,求截面ABCD的面积.
参考答案
1.A 2.B 3.B 4.79 5.220 6.20
7.解析:(1)方案1所有情况如下表:
R2
R1 (R1,R2) (R1,)
(,R2) (,)
从A到B的电路共4种等可能的结果,其中该电路为断路的有3种,
∴该电路为断路的概率为.
(2)方案2更稳定可靠.理由如下:
由(1)得方案1中电路系统正常工作的概率为1-=;
方案2中从A到B的电路的所有可能结果为(R1,R2),(R1,),(,R2),(,),共4种等可能的结果,其中电路系统正常工作有3种,∴方案2中电路系统正常工作的概率为.
∵ <,
∴方案2更稳定可靠.
8.解析:(1)如图,∵cosα=,
∴设b=x,则c=4x,由勾股定理得a==3x,
∴sinα===.
又∵β=30°,
∴sinβ=sin30°=,
∴折射率为==.
(2)根据折射率与(1)的材料相同,可得折射率为.
∵α=60°,
∴==,
∴sinβ=.
∵四边形ABCD是矩形,O是AD的中点,
∴AD=2OD,∠ADC=90°.
又∵∠OCD=β,
∴sin∠OCD=sinβ=.
在Rt△ODC中,设OD=x,OC=3x,
由勾股定理得CD==x,
∴tanβ===.
又∵CD=10cm,
∴=,
∴OD=5cm,
∴AD=10cm,
∴截面ABCD的面积为10×10=100cm2.
同课章节目录
