苏科版数学七年级下册 第9章《整式乘法与因式分解》9.4 乘法公式(含答案)
文档属性
| 名称 | 苏科版数学七年级下册 第9章《整式乘法与因式分解》9.4 乘法公式(含答案) | 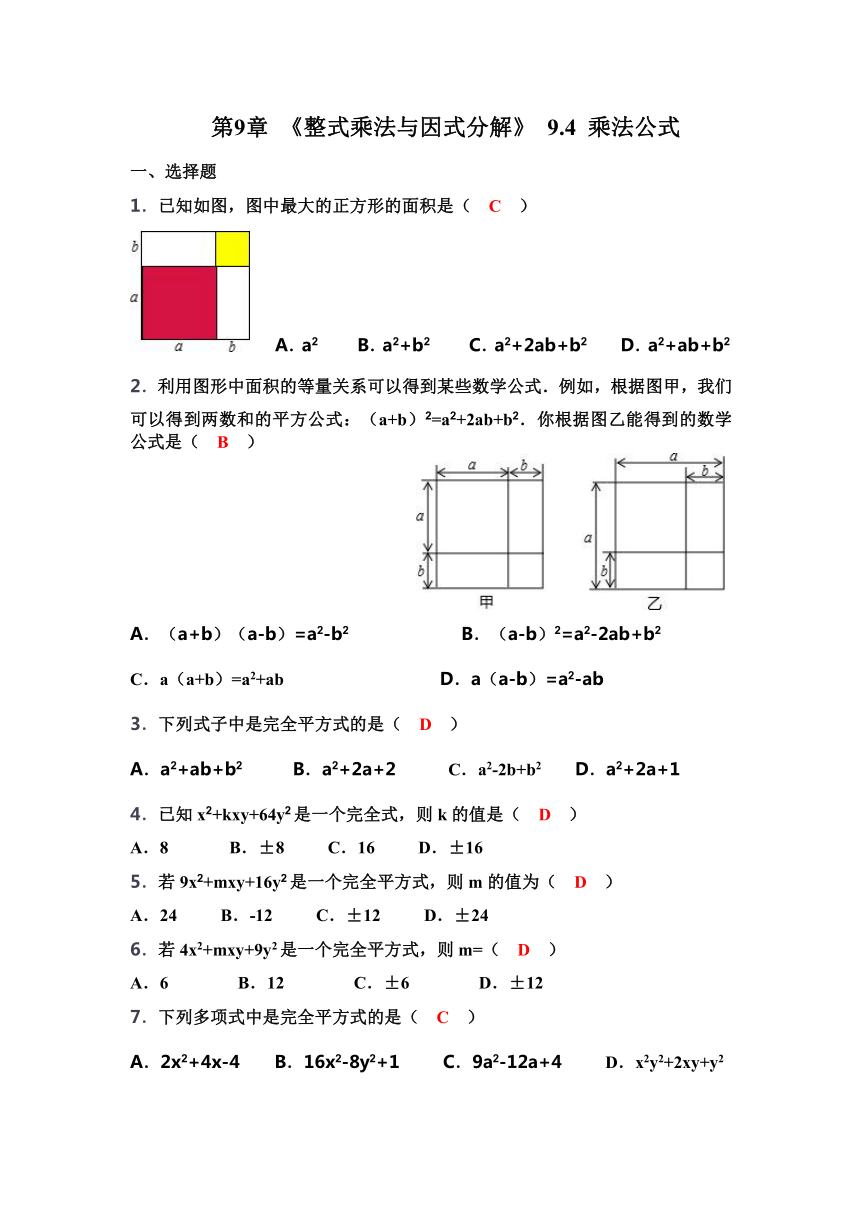 | |
| 格式 | zip | ||
| 文件大小 | 36.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-16 12:36:31 | ||
图片预览



文档简介
第9章 《整式乘法与因式分解》 9.4 乘法公式
一、选择题
1.已知如图,图中最大的正方形的面积是( C )
( http: / / www.21cnjy.com ) A.a2 B.a2+b2 C.a2+2ab+b2 D.a2+ab+b2
2.利用图形中面积的等量关系可以得到某些 ( http: / / www.21cnjy.com )数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( B )
A.(a+b)(a-b)=a2-b2 B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab D.a(a-b)=a2-ab
3.下列式子中是完全平方式的是( D )
a2+ab+b2 B.a2+2a+2 C.a2-2b+b2 D.a2+2a+1
4.已知x2+kxy+64y2是一个完全式,则k的值是( D )
A.8 B.±8 C.16 D.±16
5.若9x2+mxy+16y2是一个完全平方式,则m的值为( D )
A.24 B.-12 C.±12 D.±24
6.若4x2+mxy+9y2是一个完全平方式,则m=( D )
A.6 B.12 C.±6 D.±12
7.下列多项式中是完全平方式的是( C )
A.2x2+4x-4 B.16x2-8y2+1 C.9a2-12a+4 D.x2y2+2xy+y2
8.如果x2+mx+9是一个完全平方式,则m的值为( D )
A.3 B.6 C.±3 D.±6
9.如果x2+kx+25是一个完全平方式,那么k的值是( D )
A.5 B.±5 C.10 D.±10
10.下列各式是完全平方式的是( A )
x2-x+ B.1+x2 C.x+xy+1 D.x2+2a-1
化简求值(8分)
11.((2a+b)(2a-b)+3(a-2b)2+(-3a)(3a-4b),其中a= -1,b=-2.
解:(2a+b)(2a-b)+3(a-2b ( http: / / www.21cnjy.com ))2+(-3a)(3a-4b)
=4a2-b2+3(a2-4ab+4b2)-9a2+12ab
=4a2-b2+3a2-12ab+12b2-9a2+12ab
=-2a2+11b2,
当a=-1,b=-2时,
原式= -2×(-1)2+11×(-2)2=-2+44=42.
12.先化简,再求值:(p-1)(p+6)-(p+1)2,其中p= .
解:(p-1)(p+6)-(p+1)2,
=p2+5p-6-p2-2p-1,
=3p-7,
当p=时,原式=3×-7=2-7= -5.
13.先化简代数式,再求值:(a-1)2+a(1-a),其中a=-1.
解:方法一:原式=a2-2a+1+a-a2= -a+1,
当a=-1时,原式=-(-1)+1= -+2.
方法二:原式=(a-1)2-a(a-1)=(a-1)(a-1-a)=-a+1,
当a=-1时,原式=-(-1)+1= -+2.
14.化简求值:(2a-3b)2-(2a+3b)(2a-3b)+(2a+3b)2,其中a=-2,b=.
解:(2a-3b)2-(2a+3b)(2a ( http: / / www.21cnjy.com )-3b)+(2a+3b)2,
=4a2-12ab+9b2-4a2+9b2+4a2+12ab+9b2
=4a2+27b2,
当a=-2,b=时,原式=4×(-2)2+27×()2=16+3=19.
15.先化简,再求值:(2a+1)2-2a(2a-1),其中a=.
解:(2a+1)2-2a(2a-1),
=4a2+4a+1-4a2+2a,
=6a+1,
当a=,原式=6×+1=3+1=4.
16.先化简,再求值:8m2-5m(-m+3n)+4m(-4m-n),其中m=2,n=-1.
解:8m2-5m(-m+3n)+4m(-4m-n),
=8m2+5m2-15mn ( http: / / www.21cnjy.com )-16m2-10mn,
=-3m2-25mn,
当m=2,n=-1时,原式=-3×22-25×2×(-1)=38.
17.先化简,再求值:(a-2)(a+2)-a(a-2),其中a=-1.
解:(a-2)(a+2)-a(a-2),
=a2-4-a2+2a,
=2a-4,
当a=-1时,原式=2×(-1)-4=-6.
18.先化简,再求值:(a+b)(a-b)+(a+b)2-2a2,其中a=3,b=- .
解:(a+b)(a-b)+(a+b)2 ( http: / / www.21cnjy.com )-2a2,
=a2-b2+a2+2ab+b2-2a2,
=2ab,
当a=3,b= - 时,
原式=2×3×(- )= -2.
19.已知x2-5x=14,求(x-1)(2x-1)-(x+1)2+1的值.
解:(x-1)(2x-1)-(x+ ( http: / / www.21cnjy.com )1)2+1,
=2x2-x-2x+1-(x2+2x+1)+1,
=2x2-x-2x+1-x2-2x-1+1,
=x2-5x+1.
当x2-5x=14时,
原式=(x2-5x)+1=14+1=15.
20.先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=,b=-1.
解:(a2b-2ab2-b3)÷b ( http: / / www.21cnjy.com )-(a+b)(a-b),
=a2-2ab-b2-(a2-b2),
=a2-2ab-b2-a2+b2,
=-2ab,
当a=,b= -1时,
原式=-2× ×(-1)=1.
三、填空题
21.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k= -3 .
解 析: 根据完全平方公式的结构,按照要求x ( http: / / www.21cnjy.com )2-2x-3=x2-2x+1-4=(x-1)2-4,可知m=1.k=-4,则m+k=-3.
∵x2-2x-3=x2-2x+1-4=(x-1)2-4,
∴m=1,k= -4,
∴m+k=-3.
故填-3.
22.若(x+ )2=9,则(x - )2的值为 5 .
23.当s=t+时,代数式s2-2st+t2的值为 .
24.已知x+y=7且xy=12,则当x<y时,- 的值等于 .
解 析: 先运用完全平方 ( http: / / www.21cnjy.com )公式的变形求出y-x的值,然后代入通分后的所求式子中,计算即可.
∵x+y=7且xy=12,
∴(x-y)2=(x+y)2-4xy=72-4×12=49-48=1,
∵x<y,
∴y-x=1,
∴- ==.
点评:本题考查了完全平方公式,关键是利用(x-y)2=(x+y)2-4xy的关系进行计算.
25.若a2+b2=5,ab=2,则(a+b)2= 9 .
26.已知x+y=1,则x2+xy+y2= .
27.如图为杨辉三角表,它可以帮助我们按规律写出(a+b)n(其中n为正整数)展开式的系数,请仔细观察表中规律,填出(a+b)4的展开式中所缺的系数.
(a+b)1=a+b; ( http: / / www.21cnjy.com )
(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+ 4 a3b+ 6 a2b2+ 4 ab3+b4.
分析:观察本题的规律,下一行的数据是上一行相邻两个数的和,根据规律填入即可.
解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
28.已知x+y=17,xy=60,则x2+y2= 169 .
29.已知x- =1,则x2+= 3 .
30.x2-10x+ 25 =(x- 5 )2.
四、计算:
31.(1)(5a2+2 ( http: / / www.21cnjy.com )a)-4(2+2a2); (2)5x2(x+1)(x-1).
解: =5a2+2a-8-8a2, 解:=5x2(x2-1),
= -3a2+2a-8; =5x4-5x2.
(3)3a3b2÷a2+b (a2b-3ab-5a2b); (4)2a-5b-3a+b;
解:=3ab2+a2b2-3ab2-5a2b2, 解:= -a-4b;
= -4a2b2.
-2(2x2-xy)+4(x2+xy-1); (6)a2(a-1)+(a-5)(a+7);
解:= -4x2+2xy+4x2+4x ( http: / / www.21cnjy.com )y-4, 解: =a3-a2+a2+7a-5a-35,
= 6xy-4. =a3+2a-35;
(7)(x-5y)2-(x+5y)2 ( http: / / www.21cnjy.com ); (8)[(ab+1)(ab-1)-2a2b2+1]÷(-ab).
解:=(x-5y+x+5y)(x-5y-x-5y), 解:=(a2b2-1-2a2b2+1)÷(-ab),
= -20xy; =ab.
(9)[(x+y)2-y(2x+y)-8x]÷2x
解:=(x2+2xy+y2-2xy-y2-8x)÷2x,
=(x2-8x)÷2x,
=x-4.
五、解答题
32.按下列程序计算,把答案填写在表格内,并观察有什么规律,想想为什么有这样的规律?
(1)填写表内空格:
输入x 3 2 -2 -3 …
输出答案 1 1 …
(2)发现的规律是: .
解:(1)
输入x 3 2 -2 -3 …
输出答案 1 1 1 1 …
(2)发现的规律是:不论x取任意数输入程序后结果都是1,或(x2+x)÷x-x=x+1-x=1.
33.有一块直径为2a+b的圆形木板,挖去直径分别为2a和b的两个圆,问剩下的木板面积是多少?
解:大圆面积=π()2,小圆面积 ( http: / / www.21cnjy.com )=π()2+π()2,
所以剩下的面积=π()2-[π()2+π()2]=abπ.
故答案为:abπ.
一、选择题
1.已知如图,图中最大的正方形的面积是( C )
( http: / / www.21cnjy.com ) A.a2 B.a2+b2 C.a2+2ab+b2 D.a2+ab+b2
2.利用图形中面积的等量关系可以得到某些 ( http: / / www.21cnjy.com )数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( B )
A.(a+b)(a-b)=a2-b2 B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab D.a(a-b)=a2-ab
3.下列式子中是完全平方式的是( D )
a2+ab+b2 B.a2+2a+2 C.a2-2b+b2 D.a2+2a+1
4.已知x2+kxy+64y2是一个完全式,则k的值是( D )
A.8 B.±8 C.16 D.±16
5.若9x2+mxy+16y2是一个完全平方式,则m的值为( D )
A.24 B.-12 C.±12 D.±24
6.若4x2+mxy+9y2是一个完全平方式,则m=( D )
A.6 B.12 C.±6 D.±12
7.下列多项式中是完全平方式的是( C )
A.2x2+4x-4 B.16x2-8y2+1 C.9a2-12a+4 D.x2y2+2xy+y2
8.如果x2+mx+9是一个完全平方式,则m的值为( D )
A.3 B.6 C.±3 D.±6
9.如果x2+kx+25是一个完全平方式,那么k的值是( D )
A.5 B.±5 C.10 D.±10
10.下列各式是完全平方式的是( A )
x2-x+ B.1+x2 C.x+xy+1 D.x2+2a-1
化简求值(8分)
11.((2a+b)(2a-b)+3(a-2b)2+(-3a)(3a-4b),其中a= -1,b=-2.
解:(2a+b)(2a-b)+3(a-2b ( http: / / www.21cnjy.com ))2+(-3a)(3a-4b)
=4a2-b2+3(a2-4ab+4b2)-9a2+12ab
=4a2-b2+3a2-12ab+12b2-9a2+12ab
=-2a2+11b2,
当a=-1,b=-2时,
原式= -2×(-1)2+11×(-2)2=-2+44=42.
12.先化简,再求值:(p-1)(p+6)-(p+1)2,其中p= .
解:(p-1)(p+6)-(p+1)2,
=p2+5p-6-p2-2p-1,
=3p-7,
当p=时,原式=3×-7=2-7= -5.
13.先化简代数式,再求值:(a-1)2+a(1-a),其中a=-1.
解:方法一:原式=a2-2a+1+a-a2= -a+1,
当a=-1时,原式=-(-1)+1= -+2.
方法二:原式=(a-1)2-a(a-1)=(a-1)(a-1-a)=-a+1,
当a=-1时,原式=-(-1)+1= -+2.
14.化简求值:(2a-3b)2-(2a+3b)(2a-3b)+(2a+3b)2,其中a=-2,b=.
解:(2a-3b)2-(2a+3b)(2a ( http: / / www.21cnjy.com )-3b)+(2a+3b)2,
=4a2-12ab+9b2-4a2+9b2+4a2+12ab+9b2
=4a2+27b2,
当a=-2,b=时,原式=4×(-2)2+27×()2=16+3=19.
15.先化简,再求值:(2a+1)2-2a(2a-1),其中a=.
解:(2a+1)2-2a(2a-1),
=4a2+4a+1-4a2+2a,
=6a+1,
当a=,原式=6×+1=3+1=4.
16.先化简,再求值:8m2-5m(-m+3n)+4m(-4m-n),其中m=2,n=-1.
解:8m2-5m(-m+3n)+4m(-4m-n),
=8m2+5m2-15mn ( http: / / www.21cnjy.com )-16m2-10mn,
=-3m2-25mn,
当m=2,n=-1时,原式=-3×22-25×2×(-1)=38.
17.先化简,再求值:(a-2)(a+2)-a(a-2),其中a=-1.
解:(a-2)(a+2)-a(a-2),
=a2-4-a2+2a,
=2a-4,
当a=-1时,原式=2×(-1)-4=-6.
18.先化简,再求值:(a+b)(a-b)+(a+b)2-2a2,其中a=3,b=- .
解:(a+b)(a-b)+(a+b)2 ( http: / / www.21cnjy.com )-2a2,
=a2-b2+a2+2ab+b2-2a2,
=2ab,
当a=3,b= - 时,
原式=2×3×(- )= -2.
19.已知x2-5x=14,求(x-1)(2x-1)-(x+1)2+1的值.
解:(x-1)(2x-1)-(x+ ( http: / / www.21cnjy.com )1)2+1,
=2x2-x-2x+1-(x2+2x+1)+1,
=2x2-x-2x+1-x2-2x-1+1,
=x2-5x+1.
当x2-5x=14时,
原式=(x2-5x)+1=14+1=15.
20.先化简,再求值:(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=,b=-1.
解:(a2b-2ab2-b3)÷b ( http: / / www.21cnjy.com )-(a+b)(a-b),
=a2-2ab-b2-(a2-b2),
=a2-2ab-b2-a2+b2,
=-2ab,
当a=,b= -1时,
原式=-2× ×(-1)=1.
三、填空题
21.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k= -3 .
解 析: 根据完全平方公式的结构,按照要求x ( http: / / www.21cnjy.com )2-2x-3=x2-2x+1-4=(x-1)2-4,可知m=1.k=-4,则m+k=-3.
∵x2-2x-3=x2-2x+1-4=(x-1)2-4,
∴m=1,k= -4,
∴m+k=-3.
故填-3.
22.若(x+ )2=9,则(x - )2的值为 5 .
23.当s=t+时,代数式s2-2st+t2的值为 .
24.已知x+y=7且xy=12,则当x<y时,- 的值等于 .
解 析: 先运用完全平方 ( http: / / www.21cnjy.com )公式的变形求出y-x的值,然后代入通分后的所求式子中,计算即可.
∵x+y=7且xy=12,
∴(x-y)2=(x+y)2-4xy=72-4×12=49-48=1,
∵x<y,
∴y-x=1,
∴- ==.
点评:本题考查了完全平方公式,关键是利用(x-y)2=(x+y)2-4xy的关系进行计算.
25.若a2+b2=5,ab=2,则(a+b)2= 9 .
26.已知x+y=1,则x2+xy+y2= .
27.如图为杨辉三角表,它可以帮助我们按规律写出(a+b)n(其中n为正整数)展开式的系数,请仔细观察表中规律,填出(a+b)4的展开式中所缺的系数.
(a+b)1=a+b; ( http: / / www.21cnjy.com )
(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+ 4 a3b+ 6 a2b2+ 4 ab3+b4.
分析:观察本题的规律,下一行的数据是上一行相邻两个数的和,根据规律填入即可.
解:(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
28.已知x+y=17,xy=60,则x2+y2= 169 .
29.已知x- =1,则x2+= 3 .
30.x2-10x+ 25 =(x- 5 )2.
四、计算:
31.(1)(5a2+2 ( http: / / www.21cnjy.com )a)-4(2+2a2); (2)5x2(x+1)(x-1).
解: =5a2+2a-8-8a2, 解:=5x2(x2-1),
= -3a2+2a-8; =5x4-5x2.
(3)3a3b2÷a2+b (a2b-3ab-5a2b); (4)2a-5b-3a+b;
解:=3ab2+a2b2-3ab2-5a2b2, 解:= -a-4b;
= -4a2b2.
-2(2x2-xy)+4(x2+xy-1); (6)a2(a-1)+(a-5)(a+7);
解:= -4x2+2xy+4x2+4x ( http: / / www.21cnjy.com )y-4, 解: =a3-a2+a2+7a-5a-35,
= 6xy-4. =a3+2a-35;
(7)(x-5y)2-(x+5y)2 ( http: / / www.21cnjy.com ); (8)[(ab+1)(ab-1)-2a2b2+1]÷(-ab).
解:=(x-5y+x+5y)(x-5y-x-5y), 解:=(a2b2-1-2a2b2+1)÷(-ab),
= -20xy; =ab.
(9)[(x+y)2-y(2x+y)-8x]÷2x
解:=(x2+2xy+y2-2xy-y2-8x)÷2x,
=(x2-8x)÷2x,
=x-4.
五、解答题
32.按下列程序计算,把答案填写在表格内,并观察有什么规律,想想为什么有这样的规律?
(1)填写表内空格:
输入x 3 2 -2 -3 …
输出答案 1 1 …
(2)发现的规律是: .
解:(1)
输入x 3 2 -2 -3 …
输出答案 1 1 1 1 …
(2)发现的规律是:不论x取任意数输入程序后结果都是1,或(x2+x)÷x-x=x+1-x=1.
33.有一块直径为2a+b的圆形木板,挖去直径分别为2a和b的两个圆,问剩下的木板面积是多少?
解:大圆面积=π()2,小圆面积 ( http: / / www.21cnjy.com )=π()2+π()2,
所以剩下的面积=π()2-[π()2+π()2]=abπ.
故答案为:abπ.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
