2015—2016八年级下册数学(沪科版)同步教学课件:20.1数据的频数分布(共29张PPT)
文档属性
| 名称 | 2015—2016八年级下册数学(沪科版)同步教学课件:20.1数据的频数分布(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-16 00:00:00 | ||
图片预览








文档简介
课件29张PPT。数 学新课标(HK) 八年级下册第20章 数据的初步分析20.1 数据的频数分布 ? 学习目标1 会计算一组数据的组距、组数、频数20.1 数据的频数分布1.八年级(5)班20名女生身高数据如下(单位:cm):
153 156 152 158 156
160 163 145 152 153
162 153 165 150 157
153 158 157 157 158
(1)完成下表:20.1 数据的频数分布(2)上表把身高分成________组,组距是________;
(3)身高在__________cm范围的人数量最多.1154310150~15920.1 数据的频数分布2.某班共有学生40人,在一次数学测验中共有20人在80分以上,这次测验80分以上分数出现的频数是( )
A.20 B.0.5
C.40 D.80
3.有40个数据,其中最大值为35,最小值为16,若取组距为4,则应该分的组数是______.
3.520.1 数据的频数分布[归纳] (1)一批数据中落在某个小组内数据的个数称为这个组的频数.
(2)组数=最大值-最小值组距;
(3)组距是指把一批数据分成若干组,每个小组的两个端点间的距离.
[注意] (1)通常各组的组距应相等;
(2)各组频数之和等于数据总数;
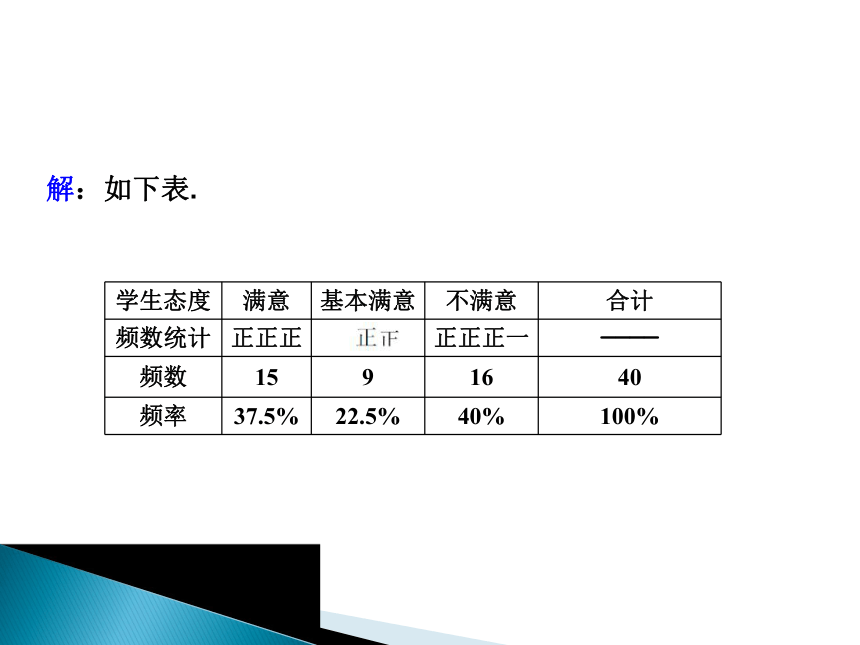
(3)有时我们还可以将发生的事件按类别进行分组,这时,频数就是各类事件发生的次数.20.1 数据的频数分布 ? 学习目标2 会列频数分布表反映数据的特征 4.八(1)班有40名学生,他们对郝老师的数学教学进行了测评,测评信息见下表.
请补全表中数据.
20.1 数据的频数分布解:如下表. 20.1 数据的频数分布[归纳] 列频数分布表的一般步骤:①计算这批数据中_______与__________的差;②决定________与________;③决定_________;④列频数分布表.最大数最小数组距组数分点20.1 数据的频数分布 ? 学习目标3 会画频数直方图反映数据的特征2720.1 数据的频数分布[归纳] (1)画出相互垂直的两条直线,用横轴表示________,纵轴表示_________,绘制出相应的长方形条,就得到了频数直方图.
(2)画频数直方图的步骤:①计算这批数据中最大数与最小数的差;②决定组距与组数;③决定分点④____________;⑤_______________.分组情况频数列频数分布表画频数直方图20.1 数据的频数分布探究问题一 计算一组数据的频率例1 已知在一个样本中,50个数据分别落在5个组内,第一、二、三、五组的频数分别为2,8,15,5,则第四组的频数和频率分别为( )
A.25,50% B.20,50%
C.20,40% D.25,40%C 20.1 数据的频数分布解:第四组的频数为50-(2+8+15+5)=20,频率为=0.4=40%,故选C.20.1 数据的频数分布[归纳总结] 频率表示一个对象出现的次数在总次数中所占的比例,它是一个比值,可用百分数表示,也可用小数或分数表示,频率p的取值范围是0≤p≤1,各类(组)数据的频率之和等于1.20.1 数据的频数分布例2 在“我喜欢的体育项目”调查活动中,小明调查了本班30人,记录结果如下:(其中喜欢打羽毛球的记为A,喜欢打乒乓球的记为B,喜欢踢足球的记为C,喜欢跑步的记为D)
求A的频率.解:A的频率= 6 = 1
30 520.1 数据的频数分布[归纳总结] (1)如果一批数据共有n个,而其中某一组数据是m个,那么就是该组数据在这批数据中出现的频率.
(2)在一批数据中,某组数据的频数m、频率p和数据总数n之间的关系是m=np.
探究问题二 从频数分布表中获取数据信息,进而用样本特征估计总体的特征20.1 数据的频数分布例3 今年3月份,某市教育局倡导中小学开展“4321”(即“四操”“三球” “二艺”“一跑”活动的简称)艺体普及活动.某校学生会为了了解全校同学对“4321”中部分项目的喜爱情况,随机调查了200名同学(每位同学仅选一项最喜爱的项目),根据调查结果制作了频数分布表:20.1 数据的频数分布(1)请补全频数分布表;
(2)在这次抽样调查中,喜爱哪个体育项目的同学最多?喜爱哪个体育项目的同学最少?
(3)根据以上调查,试估计该校1620名学生中最喜爱健美操的同学约有多少人. 20.1 数据的频数分布[解析] (1)首先根据所有频率之和为1即可求出未知的频率,然后用200分别乘以各个小组的频率就可以求出所有未知的频数,最后就可以补全频数分布表;(2)根据表格的信息即可知道喜爱哪个体育项目的同学最多,喜爱哪个体育项目的同学最少;(3)用最喜爱健美操的同学的频率乘以1620即可求出最喜爱健美操的同学的人数.20.1 数据的频数分布解:(1)1-28%-12%-24%-11%-10%=15%,
∴200×15%=30,200×28%=56,
补全频数分布表如下所示: 20.1 数据的频数分布(2)从表格中信息可知喜爱篮球的同学最多,喜爱跑步的同学最少.
(3)从表格中信息可以估计该校1620名学生中最喜爱健美操的同学约有1620×15%=243(人).[归纳总结] 1.在一组数据中,已知频数m、频率p、数据总数n中的两个值,可用公式m=np求出第三个值.
2.当已知其他各组的频率求某一组的频率时,可用1减去其他各组的频率之和来计算.探究问题三 从频数直方图中获取信息,进而用样本特征估计总体特征20.1 数据的频数分布例4实验中学为了了解本校八年级学生期末考试数学成绩,随机抽查了40名学生的成绩(分)如下:
63,84,91,53,69,81,61,69,91,78,
75,81,80,67,76,81,79,94,61,69,
89,70,70,87,81,86,90,88,85,67,
71,82,87,75,87,95,50,65,74,77.
(1) 请你将上述数据整理后,列出频数分布表,画出频数直方图;
(2) 该校八年级有360人,估计这次考试数学成绩优秀的人数(80分以上含80分).20.1 数据的频数分布[解析] (1)分析数据可得,最大值是95,最小值是50,故可求得最大值与最小值的差为45;可按组距为10对数据进行分组,由于45÷10=4.5,故组数为
5;据此可作出频数分布表和频数直方图;(2)根据频数分布表统计出优秀人数的频率来估计总体中的优秀人数.20.1 数据的频数分布解:(1)①计算最大值与最小值的差:95-50=45;②决定组数:将组距设为10,∴45÷10=4.5,∴组数为5;③决定分点和列频数分布表:20.1 数据的频数分布 ④频数直方图如图20-1-2所示: 20.1 数据的频数分布[归纳总结] 1.决定分点时,为避免数据正好落在分点上,一般把分点比原数据多取一位小数,并把第一组的起点稍微减小一点,或约定各小组包括某一组端点数据,使得数据只落在某一小组内.
2.列频数分布表的关键是分组,一般地,数据个数在100以内时,常分成5~12组.应注意:每个数据只能落在一个小组内.20.1 数据的频数分布3.频数直方图的小长方形的高与频数成正比,小长方形的高由频数大小决定,应注意:①直方图由横、纵轴和长方形三部分组成,要标清相关数据及项目,线条要清楚、规范;②每个小长方形的高表示对应组的频数,长方形之间没有空隙,易于比较各组频数;③绘频数直方图时,一般先列频数分布表,再根据频数分布表画出频数直方图.20.1 数据的频数分布20.1 数据的频数分布[反思]频数直方图和以前学习过的条形统计图有什么关系?[答案] 频数直方图和条形统计图类似,只不过频数直方图的横轴表示的是分组情况,纵轴和条形统计图一样,都是表示频数(数量).
153 156 152 158 156
160 163 145 152 153
162 153 165 150 157
153 158 157 157 158
(1)完成下表:20.1 数据的频数分布(2)上表把身高分成________组,组距是________;
(3)身高在__________cm范围的人数量最多.1154310150~15920.1 数据的频数分布2.某班共有学生40人,在一次数学测验中共有20人在80分以上,这次测验80分以上分数出现的频数是( )
A.20 B.0.5
C.40 D.80
3.有40个数据,其中最大值为35,最小值为16,若取组距为4,则应该分的组数是______.
3.520.1 数据的频数分布[归纳] (1)一批数据中落在某个小组内数据的个数称为这个组的频数.
(2)组数=最大值-最小值组距;
(3)组距是指把一批数据分成若干组,每个小组的两个端点间的距离.
[注意] (1)通常各组的组距应相等;
(2)各组频数之和等于数据总数;
(3)有时我们还可以将发生的事件按类别进行分组,这时,频数就是各类事件发生的次数.20.1 数据的频数分布 ? 学习目标2 会列频数分布表反映数据的特征 4.八(1)班有40名学生,他们对郝老师的数学教学进行了测评,测评信息见下表.
请补全表中数据.
20.1 数据的频数分布解:如下表. 20.1 数据的频数分布[归纳] 列频数分布表的一般步骤:①计算这批数据中_______与__________的差;②决定________与________;③决定_________;④列频数分布表.最大数最小数组距组数分点20.1 数据的频数分布 ? 学习目标3 会画频数直方图反映数据的特征2720.1 数据的频数分布[归纳] (1)画出相互垂直的两条直线,用横轴表示________,纵轴表示_________,绘制出相应的长方形条,就得到了频数直方图.
(2)画频数直方图的步骤:①计算这批数据中最大数与最小数的差;②决定组距与组数;③决定分点④____________;⑤_______________.分组情况频数列频数分布表画频数直方图20.1 数据的频数分布探究问题一 计算一组数据的频率例1 已知在一个样本中,50个数据分别落在5个组内,第一、二、三、五组的频数分别为2,8,15,5,则第四组的频数和频率分别为( )
A.25,50% B.20,50%
C.20,40% D.25,40%C 20.1 数据的频数分布解:第四组的频数为50-(2+8+15+5)=20,频率为=0.4=40%,故选C.20.1 数据的频数分布[归纳总结] 频率表示一个对象出现的次数在总次数中所占的比例,它是一个比值,可用百分数表示,也可用小数或分数表示,频率p的取值范围是0≤p≤1,各类(组)数据的频率之和等于1.20.1 数据的频数分布例2 在“我喜欢的体育项目”调查活动中,小明调查了本班30人,记录结果如下:(其中喜欢打羽毛球的记为A,喜欢打乒乓球的记为B,喜欢踢足球的记为C,喜欢跑步的记为D)
求A的频率.解:A的频率= 6 = 1
30 520.1 数据的频数分布[归纳总结] (1)如果一批数据共有n个,而其中某一组数据是m个,那么就是该组数据在这批数据中出现的频率.
(2)在一批数据中,某组数据的频数m、频率p和数据总数n之间的关系是m=np.
探究问题二 从频数分布表中获取数据信息,进而用样本特征估计总体的特征20.1 数据的频数分布例3 今年3月份,某市教育局倡导中小学开展“4321”(即“四操”“三球” “二艺”“一跑”活动的简称)艺体普及活动.某校学生会为了了解全校同学对“4321”中部分项目的喜爱情况,随机调查了200名同学(每位同学仅选一项最喜爱的项目),根据调查结果制作了频数分布表:20.1 数据的频数分布(1)请补全频数分布表;
(2)在这次抽样调查中,喜爱哪个体育项目的同学最多?喜爱哪个体育项目的同学最少?
(3)根据以上调查,试估计该校1620名学生中最喜爱健美操的同学约有多少人. 20.1 数据的频数分布[解析] (1)首先根据所有频率之和为1即可求出未知的频率,然后用200分别乘以各个小组的频率就可以求出所有未知的频数,最后就可以补全频数分布表;(2)根据表格的信息即可知道喜爱哪个体育项目的同学最多,喜爱哪个体育项目的同学最少;(3)用最喜爱健美操的同学的频率乘以1620即可求出最喜爱健美操的同学的人数.20.1 数据的频数分布解:(1)1-28%-12%-24%-11%-10%=15%,
∴200×15%=30,200×28%=56,
补全频数分布表如下所示: 20.1 数据的频数分布(2)从表格中信息可知喜爱篮球的同学最多,喜爱跑步的同学最少.
(3)从表格中信息可以估计该校1620名学生中最喜爱健美操的同学约有1620×15%=243(人).[归纳总结] 1.在一组数据中,已知频数m、频率p、数据总数n中的两个值,可用公式m=np求出第三个值.
2.当已知其他各组的频率求某一组的频率时,可用1减去其他各组的频率之和来计算.探究问题三 从频数直方图中获取信息,进而用样本特征估计总体特征20.1 数据的频数分布例4实验中学为了了解本校八年级学生期末考试数学成绩,随机抽查了40名学生的成绩(分)如下:
63,84,91,53,69,81,61,69,91,78,
75,81,80,67,76,81,79,94,61,69,
89,70,70,87,81,86,90,88,85,67,
71,82,87,75,87,95,50,65,74,77.
(1) 请你将上述数据整理后,列出频数分布表,画出频数直方图;
(2) 该校八年级有360人,估计这次考试数学成绩优秀的人数(80分以上含80分).20.1 数据的频数分布[解析] (1)分析数据可得,最大值是95,最小值是50,故可求得最大值与最小值的差为45;可按组距为10对数据进行分组,由于45÷10=4.5,故组数为
5;据此可作出频数分布表和频数直方图;(2)根据频数分布表统计出优秀人数的频率来估计总体中的优秀人数.20.1 数据的频数分布解:(1)①计算最大值与最小值的差:95-50=45;②决定组数:将组距设为10,∴45÷10=4.5,∴组数为5;③决定分点和列频数分布表:20.1 数据的频数分布 ④频数直方图如图20-1-2所示: 20.1 数据的频数分布[归纳总结] 1.决定分点时,为避免数据正好落在分点上,一般把分点比原数据多取一位小数,并把第一组的起点稍微减小一点,或约定各小组包括某一组端点数据,使得数据只落在某一小组内.
2.列频数分布表的关键是分组,一般地,数据个数在100以内时,常分成5~12组.应注意:每个数据只能落在一个小组内.20.1 数据的频数分布3.频数直方图的小长方形的高与频数成正比,小长方形的高由频数大小决定,应注意:①直方图由横、纵轴和长方形三部分组成,要标清相关数据及项目,线条要清楚、规范;②每个小长方形的高表示对应组的频数,长方形之间没有空隙,易于比较各组频数;③绘频数直方图时,一般先列频数分布表,再根据频数分布表画出频数直方图.20.1 数据的频数分布20.1 数据的频数分布[反思]频数直方图和以前学习过的条形统计图有什么关系?[答案] 频数直方图和条形统计图类似,只不过频数直方图的横轴表示的是分组情况,纵轴和条形统计图一样,都是表示频数(数量).
