【中片联盟】数学 8上 期中测试卷(无答案)-内蒙古通辽市科尔沁左翼中旗
文档属性
| 名称 | 【中片联盟】数学 8上 期中测试卷(无答案)-内蒙古通辽市科尔沁左翼中旗 |  | |
| 格式 | docx | ||
| 文件大小 | 165.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 09:03:21 | ||
图片预览

文档简介
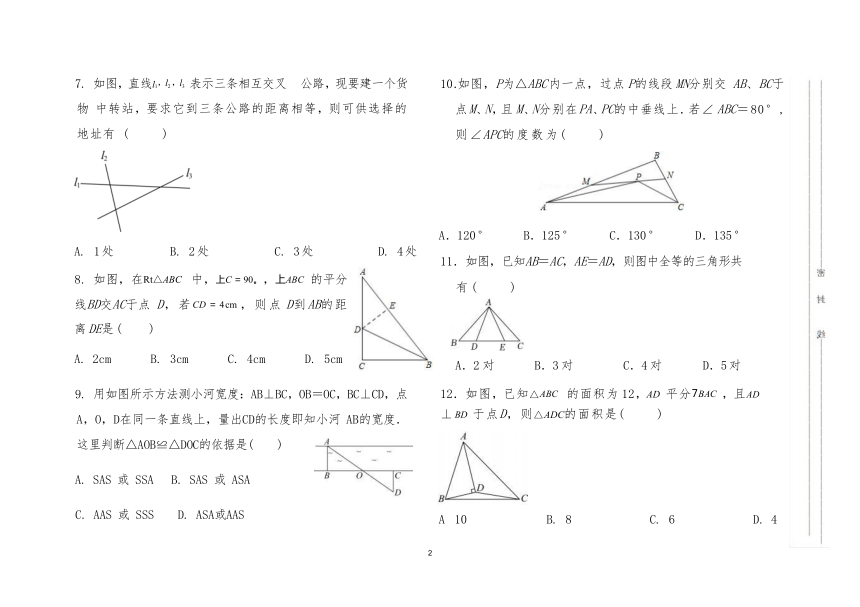
2024--2025学年上八年级数学期中试题
一、选择题(本题共 12 小题,每小题 3 分,共 36 分,将选项 写在答题卡内。
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项
1.如图图案中不是轴对称图形的是( )
A. B. C. D.
2.一副三角尺如图摆放,则 α 的大小为( )
A.105 ° B.120 ° C.135 ° D.150 °
3.下列长度的三条线段能组成三角形的是( )
A.3,4,8 B.5,6,11 C.5,6,10 D.4,4,9
4.已知,△ABC 中,AB=AC,∠A=120°, BC= 18cm,AB的垂直平分线交 BC于点M,交 AB于点 E,AC的垂直 平分线交 BC于点N,交 AB于点F,则 MN的长为( )
A.18cm B.12cm
C.6cm D.3cm
5.如图,在 Rt△ABC 中,∠C=90°,∠ABC=64°, AF ∥BE.若 BE平分∠ABC,则∠BAF=( )
A.152 ° B.148 ° C.122 ° D.116 °
△ABC 中,AC=6,中线 AD=10,则 AB边的取值范
围是( )
A.16<AB<22 B.14<AB<26 C.16<AB<26 D.14<AB<22
7. 如图,直线l1,l2 ,l3 表示三条相互交叉 公路,现要建一个货物 中转站,要求它到三条公路的距离相等,则可供选择的地址有 ( )
A. 1 处 B. 2 处 C. 3 处 D. 4 处
8. 如图,在Rt△ABC 中,上C = 90。,上ABC 的平分线 BD交 AC于点 D,若 CD = 4cm ,则点 D到AB的距离DE是( )
A. 2cm B. 3cm C. 4cm D. 5cm
9. 用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点 A,O,D在同一条直线上,量出CD的长度即知小河 AB的宽度.这里判断△AOB≌△DOC的依据是( )
SAS 或 SSA B. SAS 或 ASA
C. AAS 或 SSS D. ASA或 AAS
10.如图,P 为△ABC 内一点,过点 P 的线段 MN 分别交 AB、BC于点 M、N,且 M、N分别在 PA、PC的中垂线上.若∠ ABC=80°,则∠APC的度数为( )
A.120 ° B.125 ° C.130 ° D.135 °
如图,已知 AB=AC,AE=AD,则图中全等的三角形共
有( )
A.2 对 B.3 对 C.4 对 D.5 对
如图,已知△ABC 的面积为 12,AD 平分7BAC ,且AD ⊥ BD 于点 D,则△ADC的面积是( )
A 10 B. 8 C. 6 D. 4
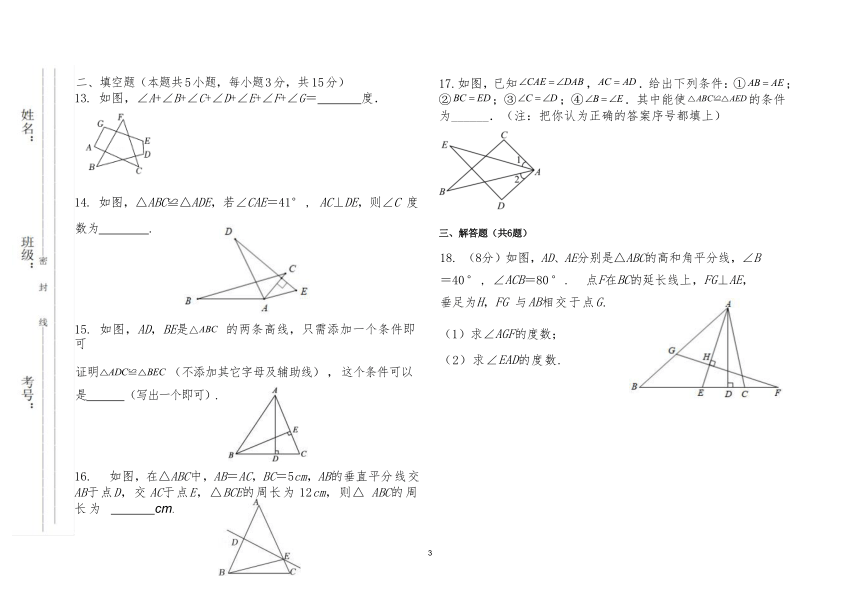
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
13. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= 度.
14. 如图,△ABC≌△ADE,若∠CAE=41° , AC⊥DE,则∠C 度
数为 .
15. 如图,AD,BE是△ABC 的两条高线,只需添加一个条件即可
证明 △ADC≌△BEC (不添加其它字母及辅助线),这个条件可以是 (写出一个即可).
如图,在△ABC 中,AB=AC,BC=5cm,AB 的垂直平分线交 AB于点D,交 AC于点E,△BCE的周长为 12cm,则△ ABC的周长为 cm.
17.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为______.(注:把你认为正确的答案序号都填上)
三、解答题(共6题)
18. (8分)如图,AD、AE分别是△ABC的高和角平分线, ∠B=40 ° , ∠ACB=80 ° . 点 F在 BC的延长线上,FG⊥AE,垂足为 H,FG 与 AB相交于点 G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
19. (8分)如图,四边形 ABCD 中,E点在 AD上,其中
∠BAE=∠BCE=∠ACD=90°,且 BC=CE,求证:△ABC与△DEC全 等.
(8分)在由单位正方形(每个小正方形边长都为 1)组成的 网格中,△AOB的顶点均在格点上.
(1)把△AOB 向左平移 4 个单位,再向上平移 2 个单位得到△ A1O1B1,请画出△A1O1B1,并写出点 A1 的坐标;
(2)请画出△AOB关于 x轴对称的△A2OB2,并求出△A2OB2 的面 积
21.(8分)如图,∠A=∠B,AE=BE,点 D在 AC边上,∠1=∠ 2,AE,BD相交于点 O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
22.(8分)如图,F、B、E、C四点共线,AB与DE相交于点O,AO=DO,OB=OE,BF=CE,求证:∠D=∠A.
23.(9分)如图,已知△ABC≌△DBE,点 D 在 AC 上,BC 与 DE 交于点 P,若 AD=DC=2.4,BC=4.1.
若∠ABE=162° , ∠DBC=30°,求∠CBE 的度数;
(2)求△DCP 与△BPE 周长和.
1
一、选择题(本题共 12 小题,每小题 3 分,共 36 分,将选项 写在答题卡内。
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项
1.如图图案中不是轴对称图形的是( )
A. B. C. D.
2.一副三角尺如图摆放,则 α 的大小为( )
A.105 ° B.120 ° C.135 ° D.150 °
3.下列长度的三条线段能组成三角形的是( )
A.3,4,8 B.5,6,11 C.5,6,10 D.4,4,9
4.已知,△ABC 中,AB=AC,∠A=120°, BC= 18cm,AB的垂直平分线交 BC于点M,交 AB于点 E,AC的垂直 平分线交 BC于点N,交 AB于点F,则 MN的长为( )
A.18cm B.12cm
C.6cm D.3cm
5.如图,在 Rt△ABC 中,∠C=90°,∠ABC=64°, AF ∥BE.若 BE平分∠ABC,则∠BAF=( )
A.152 ° B.148 ° C.122 ° D.116 °
△ABC 中,AC=6,中线 AD=10,则 AB边的取值范
围是( )
A.16<AB<22 B.14<AB<26 C.16<AB<26 D.14<AB<22
7. 如图,直线l1,l2 ,l3 表示三条相互交叉 公路,现要建一个货物 中转站,要求它到三条公路的距离相等,则可供选择的地址有 ( )
A. 1 处 B. 2 处 C. 3 处 D. 4 处
8. 如图,在Rt△ABC 中,上C = 90。,上ABC 的平分线 BD交 AC于点 D,若 CD = 4cm ,则点 D到AB的距离DE是( )
A. 2cm B. 3cm C. 4cm D. 5cm
9. 用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点 A,O,D在同一条直线上,量出CD的长度即知小河 AB的宽度.这里判断△AOB≌△DOC的依据是( )
SAS 或 SSA B. SAS 或 ASA
C. AAS 或 SSS D. ASA或 AAS
10.如图,P 为△ABC 内一点,过点 P 的线段 MN 分别交 AB、BC于点 M、N,且 M、N分别在 PA、PC的中垂线上.若∠ ABC=80°,则∠APC的度数为( )
A.120 ° B.125 ° C.130 ° D.135 °
如图,已知 AB=AC,AE=AD,则图中全等的三角形共
有( )
A.2 对 B.3 对 C.4 对 D.5 对
如图,已知△ABC 的面积为 12,AD 平分7BAC ,且AD ⊥ BD 于点 D,则△ADC的面积是( )
A 10 B. 8 C. 6 D. 4
二、填空题(本题共 5 小题,每小题 3 分,共 15 分)
13. 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G= 度.
14. 如图,△ABC≌△ADE,若∠CAE=41° , AC⊥DE,则∠C 度
数为 .
15. 如图,AD,BE是△ABC 的两条高线,只需添加一个条件即可
证明 △ADC≌△BEC (不添加其它字母及辅助线),这个条件可以是 (写出一个即可).
如图,在△ABC 中,AB=AC,BC=5cm,AB 的垂直平分线交 AB于点D,交 AC于点E,△BCE的周长为 12cm,则△ ABC的周长为 cm.
17.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为______.(注:把你认为正确的答案序号都填上)
三、解答题(共6题)
18. (8分)如图,AD、AE分别是△ABC的高和角平分线, ∠B=40 ° , ∠ACB=80 ° . 点 F在 BC的延长线上,FG⊥AE,垂足为 H,FG 与 AB相交于点 G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
19. (8分)如图,四边形 ABCD 中,E点在 AD上,其中
∠BAE=∠BCE=∠ACD=90°,且 BC=CE,求证:△ABC与△DEC全 等.
(8分)在由单位正方形(每个小正方形边长都为 1)组成的 网格中,△AOB的顶点均在格点上.
(1)把△AOB 向左平移 4 个单位,再向上平移 2 个单位得到△ A1O1B1,请画出△A1O1B1,并写出点 A1 的坐标;
(2)请画出△AOB关于 x轴对称的△A2OB2,并求出△A2OB2 的面 积
21.(8分)如图,∠A=∠B,AE=BE,点 D在 AC边上,∠1=∠ 2,AE,BD相交于点 O.
(1)求证:△AEC≌△BED;
(2)若∠2=70°,求∠AEB的度数.
22.(8分)如图,F、B、E、C四点共线,AB与DE相交于点O,AO=DO,OB=OE,BF=CE,求证:∠D=∠A.
23.(9分)如图,已知△ABC≌△DBE,点 D 在 AC 上,BC 与 DE 交于点 P,若 AD=DC=2.4,BC=4.1.
若∠ABE=162° , ∠DBC=30°,求∠CBE 的度数;
(2)求△DCP 与△BPE 周长和.
1
同课章节目录
