5.2.2 解一元二次方程- 移项 导学案(无答案) 2024--2025学年人教版七年级数学上册
文档属性
| 名称 | 5.2.2 解一元二次方程- 移项 导学案(无答案) 2024--2025学年人教版七年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 68.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 22:02:08 | ||
图片预览

文档简介
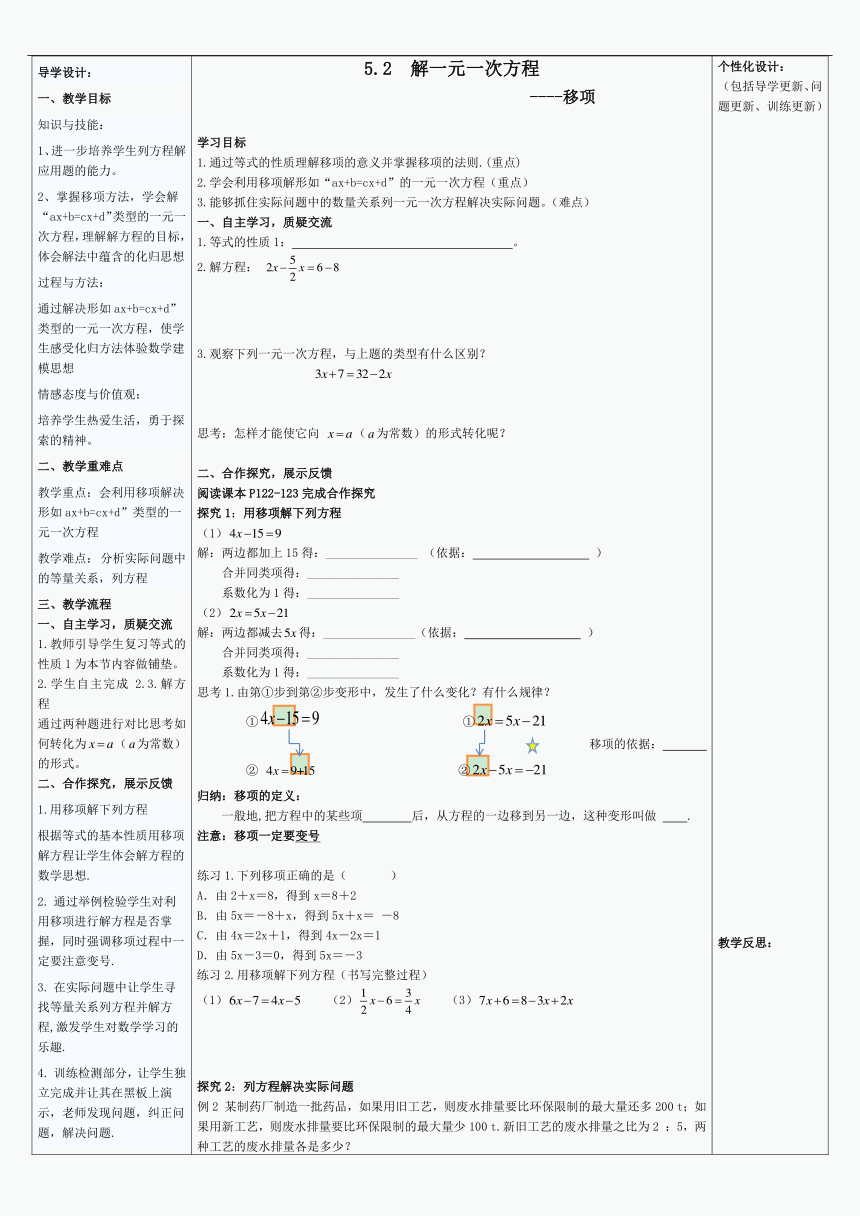
导学设计: 一、教学目标 知识与技能: 1、进一步培养学生列方程解应用题的能力。 2、掌握移项方法,学会解“ax+b=cx+d”类型的一元一次方程,理解解方程的目标,体会解法中蕴含的化归思想 过程与方法: 通过解决形如ax+b=cx+d”类型的一元一次方程,使学生感受化归方法体验数学建模思想 情感态度与价值观: 培养学生热爱生活,勇于探索的精神。 二、教学重难点 教学重点:会利用移项解决形如ax+b=cx+d”类型的一元一次方程 教学难点: 分析实际问题中的等量关系,列方程 教学流程 一、自主学习,质疑交流 1.教师引导学生复习等式的性质1为本节内容做铺垫。 2.学生自主完成2.3.解方程 通过两种题进行对比思考如何转化为(为常数)的形式。 二、合作探究,展示反馈 1.用移项解下列方程 根据等式的基本性质用移项解方程让学生体会解方程的数学思想. 通过举例检验学生对利用移项进行解方程是否掌握,同时强调移项过程中一定要注意变号. 在实际问题中让学生寻找等量关系列方程并解方程,激发学生对数学学习的乐趣. 训练检测部分,让学生独立完成并让其在黑板上演示,老师发现问题,纠正问题,解决问题. 教师多强调列方程解应用题的步骤。 教师反复强调移项要变号 四、板书设计 (
课题
利用等式的性质解方程
简化
) 5.2 解一元一次方程 ----移项 学习目标 1.通过等式的性质理解移项的意义并掌握移项的法则.(重点) 2.学会利用移项解形如“ax+b=cx+d”的一元一次方程(重点) 3.能够抓住实际问题中的数量关系列一元一次方程解决实际问题。(难点) 一、自主学习,质疑交流 1.等式的性质1: 。 2.解方程: 3.观察下列一元一次方程,与上题的类型有什么区别? 思考:怎样才能使它向 (为常数)的形式转化呢? 二、合作探究,展示反馈 阅读课本P122-123完成合作探究 探究1:用移项解下列方程 解:两边都加上15得:_______________ (依据: ) 合并同类项得:_______________ 系数化为1得:_______________ (2) 解:两边都减去得:_______________(依据: ) 合并同类项得:_______________ 系数化为1得:_______________ 思考1.由第①步到第②步变形中,发生了什么变化?有什么规律? ① ① 移项的依据: ② ② 归纳:移项的定义: 一般地,把方程中的某些项 后,从方程的一边移到另一边,这种变形叫做 . 注意:移项一定要变号 练习1.下列移项正确的是( ) A.由2+x=8,得到x=8+2 B.由5x=-8+x,得到5x+x= -8 C.由4x=2x+1,得到4x-2x=1 D.由5x-3=0,得到5x=-3 练习2.用移项解下列方程(书写完整过程) (1) (2) (3) 探究2:列方程解决实际问题 例2 某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2 :5,两种工艺的废水排量各是多少? 思考:在解决实际问题时的一般步骤是什么: , 2. , 3. , 4. , 5. , 三、归纳总结,训练检测 (一)本节课你学会了什么? (二)完成下列习题 1.下列变形正确的是( ) A.从得到 B.从得到 C.从得到 D.从得到 2.方程移项后,正确的是( ) A. B. C. D. 3.方程的解是( ) A. B. C. D. 4解下列方程 (2) 5.下面是两种移动电话计费方式: 方式一方式二月租费50元/月10元/月本地通话费0.30元/分0.5元/分
问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样? 个性化设计: (包括导学更新、问题更新、训练更新) 教学反思: 等级评价: 优( ) 良( ) 一般( ) 组长签字:
课题
利用等式的性质解方程
简化
) 5.2 解一元一次方程 ----移项 学习目标 1.通过等式的性质理解移项的意义并掌握移项的法则.(重点) 2.学会利用移项解形如“ax+b=cx+d”的一元一次方程(重点) 3.能够抓住实际问题中的数量关系列一元一次方程解决实际问题。(难点) 一、自主学习,质疑交流 1.等式的性质1: 。 2.解方程: 3.观察下列一元一次方程,与上题的类型有什么区别? 思考:怎样才能使它向 (为常数)的形式转化呢? 二、合作探究,展示反馈 阅读课本P122-123完成合作探究 探究1:用移项解下列方程 解:两边都加上15得:_______________ (依据: ) 合并同类项得:_______________ 系数化为1得:_______________ (2) 解:两边都减去得:_______________(依据: ) 合并同类项得:_______________ 系数化为1得:_______________ 思考1.由第①步到第②步变形中,发生了什么变化?有什么规律? ① ① 移项的依据: ② ② 归纳:移项的定义: 一般地,把方程中的某些项 后,从方程的一边移到另一边,这种变形叫做 . 注意:移项一定要变号 练习1.下列移项正确的是( ) A.由2+x=8,得到x=8+2 B.由5x=-8+x,得到5x+x= -8 C.由4x=2x+1,得到4x-2x=1 D.由5x-3=0,得到5x=-3 练习2.用移项解下列方程(书写完整过程) (1) (2) (3) 探究2:列方程解决实际问题 例2 某制药厂制造一批药品,如果用旧工艺,则废水排量要比环保限制的最大量还多200 t;如果用新工艺,则废水排量要比环保限制的最大量少100 t.新旧工艺的废水排量之比为2 :5,两种工艺的废水排量各是多少? 思考:在解决实际问题时的一般步骤是什么: , 2. , 3. , 4. , 5. , 三、归纳总结,训练检测 (一)本节课你学会了什么? (二)完成下列习题 1.下列变形正确的是( ) A.从得到 B.从得到 C.从得到 D.从得到 2.方程移项后,正确的是( ) A. B. C. D. 3.方程的解是( ) A. B. C. D. 4解下列方程 (2) 5.下面是两种移动电话计费方式: 方式一方式二月租费50元/月10元/月本地通话费0.30元/分0.5元/分
问:一个月内,通话时间是多少分钟时,两种移动电话计费方式的费用一样? 个性化设计: (包括导学更新、问题更新、训练更新) 教学反思: 等级评价: 优( ) 良( ) 一般( ) 组长签字:
同课章节目录
