2024-2025学年四川省成都市蓉城联盟高二(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省成都市蓉城联盟高二(上)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 431.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 14:53:17 | ||
图片预览




文档简介
2024-2025学年四川省成都市蓉城联盟高二(上)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某校高一年级有名学生,现用比例分配的分层随机抽样方法抽取一个容量为的样本,其中抽取男生和女生的人数分别为,,则该校高一年级的女生人数为( )
A. B. C. D.
2.年度最具幸福感城市调查推选活动于月日正式启动,在个地级及以上的候选城市名单中,成都市入选“幸福感指数”是指某个人主观地评价他对自己目前生活状态满意程度的指标,常用区间内的一个数来表示,该数越接近表示满意度越高,现随机抽取位成都市居民,他们的幸福感指数分别为,,,,,,,,,,则下列说法错误的是( )
A. 该组数据的第百分位数为 B. 该组数据的极差为
C. 该组数据的平均数为 D. 该组数据的中位数为
3.已知为空间内任意一点,,,,四点共面,且任意三点不共线,若,则( )
A. B. C. D.
4.年进入月后,成都市持续高温,气象局一般会提前发布高温红色预警信号高温红色预警标准为小时内最高气温将升至以上,在月日后的天中,每一天最高气温在以上的概率为用计算机生成了组随机数,结果如下:
若用,,,表示非高温红色预警,用,,,,,表示高温红色预警,则月日后的天中恰有天发布高温红色预警信号的概率为( )
A. B. C. D.
5.已知,是一个随机试验中的两个随机事件,若,,,则事件与事件的关系为( )
A. B. 互斥但不对立 C. 互为对立 D. 相互独立
6.如图,在三棱锥中,,为的中点,,则( )
A. B.
C. D.
7.在空间直角坐标系中,已知平面过点,且以向量为法向量,则平面的方程为若平面的方程为,则点到平面的距离为( )
A. B. C. D.
8.如图,在斜三棱柱中,底面为正三角形,为的中点,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
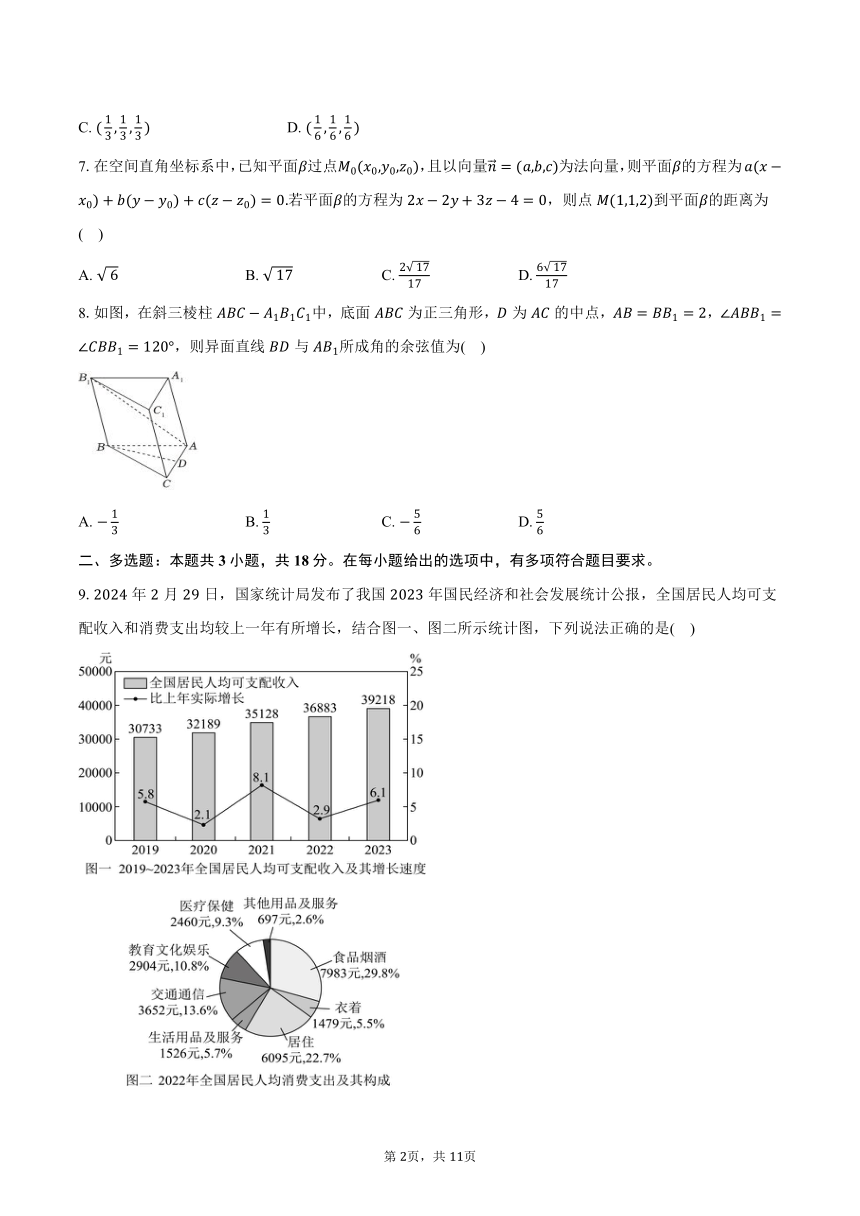
9.年月日,国家统计局发布了我国年国民经济和社会发展统计公报,全国居民人均可支配收入和消费支出均较上一年有所增长,结合图一、图二所示统计图,下列说法正确的是( )
A. 年全国居民人均可支配收入逐年递增
B. 年全国居民人均可支配收入增长速度逐年递增
C. 年全国居民人均消费支出中教育文化娱乐支出费用最少
D. 年全国居民人均消费支出中食品烟酒和居住支出费用之和占比不足
10.一个袋子中有个白球,个黄球,采用不放回的方式从中依次随机抽取个球,已知取出的个球颜色不同的概率为,则( )
A. B. C. D.
11.在棱长为的正方体中,点在底面内含边界,为棱的中点,下列说法正确的是( )
A. 满足平面的点的轨迹长度为
B. 若点在棱上运动,则点到直线的距离的最小值为
C. 若平面,则点是上靠近点的四等分点
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知空间向量,,若,则 ______.
13.月日是世界防治肥胖日我国超过一半的成年人属于超重或肥胖,岁的儿童青少年肥胖率接近,肥胖已成为严重危害我国居民健康的公共卫生问题目前,国际上常用身体质量指数,缩写来衡量人体胖瘦程度以及是否健康我国成人的数值标准为为偏瘦;为正常;为偏胖;为肥胖某校为了解学生的健康状况,研究人员从学生的体测数据中,用按比例分配的分层随机抽样方法抽取样本,样本中有名女生,女生的值的平均数为,方差为;有名男生,男生的值的平均数为,方差为则样本中所有学生的值的方差为______.
14.如图,在直三棱柱中,,,,分别为棱,上的动点,且,,,设直线与直线所成角为,若平面,则的最小值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
庚子新春,“新冠”肆虐,面对新冠肺炎的发生,某医疗小组提出了一种治疗的新方案为测试该方案的治疗效果,此医疗小组选取了患病程度相同的名病人志愿者,将他们随机分成两组,每组人第一组用新方案治疗,第二组用旧方案治疗统计病人的痊愈时间单位:天如下表:
新方案治疗
旧方案治疗
记新方案和旧方案治疗病人痊愈时间的平均数分别为和,方差分别为和.
求,,,;
判断新方案的治疗效果较旧方案是否有显著提高.
说明:如果,则认为新方案的治疗效果较旧方案是有显著提高,否则不认为有显著提高.
16.本小题分
届是四川省新高考的第一届根据新高考改革方案,年将采用“”的高考模式,“”指语文、数学、外语三门统考学科,以原始分数计入高考成绩;“”指考生从物理、历史两门学科中首选一门学科,以原始分数计入高考成绩;“”指考生从政治、地理、化学、生物学四门学科中再选两门学科,以等级分计入高考成绩按照方案,再选学科的等级分赋分规则如下,将考生原始成绩从高到低划分为,,,,五个等级,各等级人数所占比例及赋分区间如下表:
等级
人数比例
赋分区间
为让学生适应新高考的赋分模式,某市在高二的调研考试中对学生的再选学科成绩进行赋分,已知该市本次高二调研考试化学学科考试满分为分,现从该市本次高二调研考试的化学成绩中随机选取名学生的原始成绩进行分析,其频率分布直方图如图所示.
求出图中的值,并用样本估计总体的方法估计该市本次化学原始成绩等级中的最低分含等级;
为更充分发挥调研考试的作用,更有效地指导教师的教和学生的学,若采用分层抽样的方法,从原始成绩在和内的学生中共抽取人,查看他们的答题情况来分析知识点上的缺漏,再从中选取人进行个案分析,求这人中恰有人原始成绩在内的概率.
17.本小题分
如图,在四棱锥中,底面为正方形,底面,,为线段的中点.
证明:平面平面;
求直线与平面所成角的正弦值.
18.本小题分
中国乒乓球队是中国体育军团的王牌之师,屡次在国际大赛上争金夺银,被体育迷们习惯地称为“梦之队”年巴黎奥运会,中国乒乓球队包揽全部五枚金牌其中团体赛由四场单打和一场双打比赛组成,采用五场三胜制每个队由三名运动员组成,当一个队赢得三场比赛时,比赛结束年月日,中国队对战瑞典队,最终以:取得团体赛冠军,赛前某乒乓球爱好者对赛事情况进行分析,根据以往战绩,中国队在每场比赛中获胜的概率均为.
求中国队以:的比分获胜的概率;
求中国队在已输一场的情况下获胜的概率;
求至多进行四场比赛的概率.
19.本小题分
柯西是一位伟大的法国数学家,许多数学定理和结论都以他的名字命名,柯西不等式就是其中之一,它在数学的众多分支中有精彩应用柯西不等式的一般形式为:设,,,,,,,,,,则,当且仅当或存在一个数,使得时,等号成立如图,直三棱柱的体积为,的面积为.
求点到平面的距离;
若,平面平面,,分别为,上的动点,且,.
用,来表示线段的长度;
当线段的长度最小时,求平面与平面夹角的余弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由已知可得,
,
同理可得,,
;
,且,
新方案的治疗效果较旧方案有显著提高.
16.解:根据题意可得,,
原始成绩等级及以上占比,的频率为,的频率为,
原始成绩等级的最低分落在内,设为,
则,解得,
该市本次化学原始成绩等级中的最低分为分;
原始成绩在和的频率之比为:,
在内抽取人,记为,,
在内抽取人,记为,,,,
从中这人中再选取人所得样本空间为:
,
,
设“这人中恰有人原始成绩在内”,
则,
,,
这人中恰有人原始成绩在内的概率为.
17.解:证明:建立如图所示的空间直角坐标系,设,
则,,,,,
,,,,
设平面的一个法向量为,
则,则,
令,则,,,
设平面的一个法向量为,
则,则,
令,则,,,
,,
平面平面;
设平面的一个法向量为,
则,则,
令,则,,,
设直线与平面所成角为,
,
,
,
直线与平面所成角的正弦值为.
18.解:若根据以往战绩,中国队在每场比赛中获胜的概率均为,
设事件“中国队以:的比分获胜”,
中国队在每一场中获胜的概率均为,
,
中国队以:的比分获胜的概率为;
设事件“中国队在已输一场的情况下获胜”,则有两类情况:
设事件“中国队在二到四场中胜两场,再胜第五场”,
,
设事件“中国队从第二场开始连胜三场”,
,
与是互斥事件,
,
中国队在已输一场的情况下获胜的概率为;
设中国队进行三场、四场比赛获胜分别为事件、,瑞典队进行三场、四场比赛获胜分别为事件、,至多进行四场比赛为事件,
,,
,,
,,,是互斥事件,
,
至多进行四场比赛的概率为.
19.解:设点到平面的距离为,
由已知可得:,
,
即点到平面的距离为.
取的中点,连接,
,,
又平面平面且交线为,平面,
平面,平面,,
又,且,,平面,
平面,
平面,
,
可建立如图所示的空间直角坐标系,
由可知,,,
在中,,,
,,,
,,,
同理可得,
;
令
,
当且仅当,即时取等号,
当线段的长度最小时,,,,,
设平面的一个法向量为,
则,,
令,则,,
设平面的一个法向量为,,,
则,
可得平面的一个法向量为,
设平面与的夹角为,
,
平面与平面夹角的余弦值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.某校高一年级有名学生,现用比例分配的分层随机抽样方法抽取一个容量为的样本,其中抽取男生和女生的人数分别为,,则该校高一年级的女生人数为( )
A. B. C. D.
2.年度最具幸福感城市调查推选活动于月日正式启动,在个地级及以上的候选城市名单中,成都市入选“幸福感指数”是指某个人主观地评价他对自己目前生活状态满意程度的指标,常用区间内的一个数来表示,该数越接近表示满意度越高,现随机抽取位成都市居民,他们的幸福感指数分别为,,,,,,,,,,则下列说法错误的是( )
A. 该组数据的第百分位数为 B. 该组数据的极差为
C. 该组数据的平均数为 D. 该组数据的中位数为
3.已知为空间内任意一点,,,,四点共面,且任意三点不共线,若,则( )
A. B. C. D.
4.年进入月后,成都市持续高温,气象局一般会提前发布高温红色预警信号高温红色预警标准为小时内最高气温将升至以上,在月日后的天中,每一天最高气温在以上的概率为用计算机生成了组随机数,结果如下:
若用,,,表示非高温红色预警,用,,,,,表示高温红色预警,则月日后的天中恰有天发布高温红色预警信号的概率为( )
A. B. C. D.
5.已知,是一个随机试验中的两个随机事件,若,,,则事件与事件的关系为( )
A. B. 互斥但不对立 C. 互为对立 D. 相互独立
6.如图,在三棱锥中,,为的中点,,则( )
A. B.
C. D.
7.在空间直角坐标系中,已知平面过点,且以向量为法向量,则平面的方程为若平面的方程为,则点到平面的距离为( )
A. B. C. D.
8.如图,在斜三棱柱中,底面为正三角形,为的中点,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.年月日,国家统计局发布了我国年国民经济和社会发展统计公报,全国居民人均可支配收入和消费支出均较上一年有所增长,结合图一、图二所示统计图,下列说法正确的是( )
A. 年全国居民人均可支配收入逐年递增
B. 年全国居民人均可支配收入增长速度逐年递增
C. 年全国居民人均消费支出中教育文化娱乐支出费用最少
D. 年全国居民人均消费支出中食品烟酒和居住支出费用之和占比不足
10.一个袋子中有个白球,个黄球,采用不放回的方式从中依次随机抽取个球,已知取出的个球颜色不同的概率为,则( )
A. B. C. D.
11.在棱长为的正方体中,点在底面内含边界,为棱的中点,下列说法正确的是( )
A. 满足平面的点的轨迹长度为
B. 若点在棱上运动,则点到直线的距离的最小值为
C. 若平面,则点是上靠近点的四等分点
D. 的最小值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知空间向量,,若,则 ______.
13.月日是世界防治肥胖日我国超过一半的成年人属于超重或肥胖,岁的儿童青少年肥胖率接近,肥胖已成为严重危害我国居民健康的公共卫生问题目前,国际上常用身体质量指数,缩写来衡量人体胖瘦程度以及是否健康我国成人的数值标准为为偏瘦;为正常;为偏胖;为肥胖某校为了解学生的健康状况,研究人员从学生的体测数据中,用按比例分配的分层随机抽样方法抽取样本,样本中有名女生,女生的值的平均数为,方差为;有名男生,男生的值的平均数为,方差为则样本中所有学生的值的方差为______.
14.如图,在直三棱柱中,,,,分别为棱,上的动点,且,,,设直线与直线所成角为,若平面,则的最小值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
庚子新春,“新冠”肆虐,面对新冠肺炎的发生,某医疗小组提出了一种治疗的新方案为测试该方案的治疗效果,此医疗小组选取了患病程度相同的名病人志愿者,将他们随机分成两组,每组人第一组用新方案治疗,第二组用旧方案治疗统计病人的痊愈时间单位:天如下表:
新方案治疗
旧方案治疗
记新方案和旧方案治疗病人痊愈时间的平均数分别为和,方差分别为和.
求,,,;
判断新方案的治疗效果较旧方案是否有显著提高.
说明:如果,则认为新方案的治疗效果较旧方案是有显著提高,否则不认为有显著提高.
16.本小题分
届是四川省新高考的第一届根据新高考改革方案,年将采用“”的高考模式,“”指语文、数学、外语三门统考学科,以原始分数计入高考成绩;“”指考生从物理、历史两门学科中首选一门学科,以原始分数计入高考成绩;“”指考生从政治、地理、化学、生物学四门学科中再选两门学科,以等级分计入高考成绩按照方案,再选学科的等级分赋分规则如下,将考生原始成绩从高到低划分为,,,,五个等级,各等级人数所占比例及赋分区间如下表:
等级
人数比例
赋分区间
为让学生适应新高考的赋分模式,某市在高二的调研考试中对学生的再选学科成绩进行赋分,已知该市本次高二调研考试化学学科考试满分为分,现从该市本次高二调研考试的化学成绩中随机选取名学生的原始成绩进行分析,其频率分布直方图如图所示.
求出图中的值,并用样本估计总体的方法估计该市本次化学原始成绩等级中的最低分含等级;
为更充分发挥调研考试的作用,更有效地指导教师的教和学生的学,若采用分层抽样的方法,从原始成绩在和内的学生中共抽取人,查看他们的答题情况来分析知识点上的缺漏,再从中选取人进行个案分析,求这人中恰有人原始成绩在内的概率.
17.本小题分
如图,在四棱锥中,底面为正方形,底面,,为线段的中点.
证明:平面平面;
求直线与平面所成角的正弦值.
18.本小题分
中国乒乓球队是中国体育军团的王牌之师,屡次在国际大赛上争金夺银,被体育迷们习惯地称为“梦之队”年巴黎奥运会,中国乒乓球队包揽全部五枚金牌其中团体赛由四场单打和一场双打比赛组成,采用五场三胜制每个队由三名运动员组成,当一个队赢得三场比赛时,比赛结束年月日,中国队对战瑞典队,最终以:取得团体赛冠军,赛前某乒乓球爱好者对赛事情况进行分析,根据以往战绩,中国队在每场比赛中获胜的概率均为.
求中国队以:的比分获胜的概率;
求中国队在已输一场的情况下获胜的概率;
求至多进行四场比赛的概率.
19.本小题分
柯西是一位伟大的法国数学家,许多数学定理和结论都以他的名字命名,柯西不等式就是其中之一,它在数学的众多分支中有精彩应用柯西不等式的一般形式为:设,,,,,,,,,,则,当且仅当或存在一个数,使得时,等号成立如图,直三棱柱的体积为,的面积为.
求点到平面的距离;
若,平面平面,,分别为,上的动点,且,.
用,来表示线段的长度;
当线段的长度最小时,求平面与平面夹角的余弦值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由已知可得,
,
同理可得,,
;
,且,
新方案的治疗效果较旧方案有显著提高.
16.解:根据题意可得,,
原始成绩等级及以上占比,的频率为,的频率为,
原始成绩等级的最低分落在内,设为,
则,解得,
该市本次化学原始成绩等级中的最低分为分;
原始成绩在和的频率之比为:,
在内抽取人,记为,,
在内抽取人,记为,,,,
从中这人中再选取人所得样本空间为:
,
,
设“这人中恰有人原始成绩在内”,
则,
,,
这人中恰有人原始成绩在内的概率为.
17.解:证明:建立如图所示的空间直角坐标系,设,
则,,,,,
,,,,
设平面的一个法向量为,
则,则,
令,则,,,
设平面的一个法向量为,
则,则,
令,则,,,
,,
平面平面;
设平面的一个法向量为,
则,则,
令,则,,,
设直线与平面所成角为,
,
,
,
直线与平面所成角的正弦值为.
18.解:若根据以往战绩,中国队在每场比赛中获胜的概率均为,
设事件“中国队以:的比分获胜”,
中国队在每一场中获胜的概率均为,
,
中国队以:的比分获胜的概率为;
设事件“中国队在已输一场的情况下获胜”,则有两类情况:
设事件“中国队在二到四场中胜两场,再胜第五场”,
,
设事件“中国队从第二场开始连胜三场”,
,
与是互斥事件,
,
中国队在已输一场的情况下获胜的概率为;
设中国队进行三场、四场比赛获胜分别为事件、,瑞典队进行三场、四场比赛获胜分别为事件、,至多进行四场比赛为事件,
,,
,,
,,,是互斥事件,
,
至多进行四场比赛的概率为.
19.解:设点到平面的距离为,
由已知可得:,
,
即点到平面的距离为.
取的中点,连接,
,,
又平面平面且交线为,平面,
平面,平面,,
又,且,,平面,
平面,
平面,
,
可建立如图所示的空间直角坐标系,
由可知,,,
在中,,,
,,,
,,,
同理可得,
;
令
,
当且仅当,即时取等号,
当线段的长度最小时,,,,,
设平面的一个法向量为,
则,,
令,则,,
设平面的一个法向量为,,,
则,
可得平面的一个法向量为,
设平面与的夹角为,
,
平面与平面夹角的余弦值为.
第1页,共1页
同课章节目录
