3 图形的基本性质与三角形(含答案)2025年中考数学总复习专题练(河北)
文档属性
| 名称 | 3 图形的基本性质与三角形(含答案)2025年中考数学总复习专题练(河北) |  | |
| 格式 | docx | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 18:33:26 | ||
图片预览




文档简介
3图形的基本性质与三角形
题号 一 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 线段的中点,线段的和差、角度计算,方位角,余角和(邻)补角,度、分、秒的简单换算.立体图形与平面图形.相交线,垂直的意义及性质,距离(点到线,点到点,垂线段),平行线的性质定理和判定定理及平行于同一条直线的两条直线平行,相关证明,图形的展开与折叠.基本事实:两点确定一条直线,两点之间线段最短、过一点有且只有一条直线与已知直线垂直,尺规作图;三角形的相关概念,内角和定理及推论,三边关系,三角形的全等,等腰(等边)三角形的性质定理和判定定理,直角三角形的性质定理和判定、勾股定理及其逆定理,角平分线性质定理及其逆定理,线段垂直平分线性质定理及其逆定理,定义、命题、定理
一、选择题(本大题共16个小题,共 38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,∠AOD-∠AOC等于 ( )
A.∠AOC B.∠BOC C.∠BOD D.∠COD
2.图中的三角形被木板遮住了一部分,这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
3.下列几何图形中,不一定是轴对称图形的是 ( )
A.等腰三角形 B.直角三角形
C.矩形 D.等边三角形
4.已知△ABC的三边长分别为a,2,5,那么a的值可以是 ( )
A.2 B.3 C.5 D.7
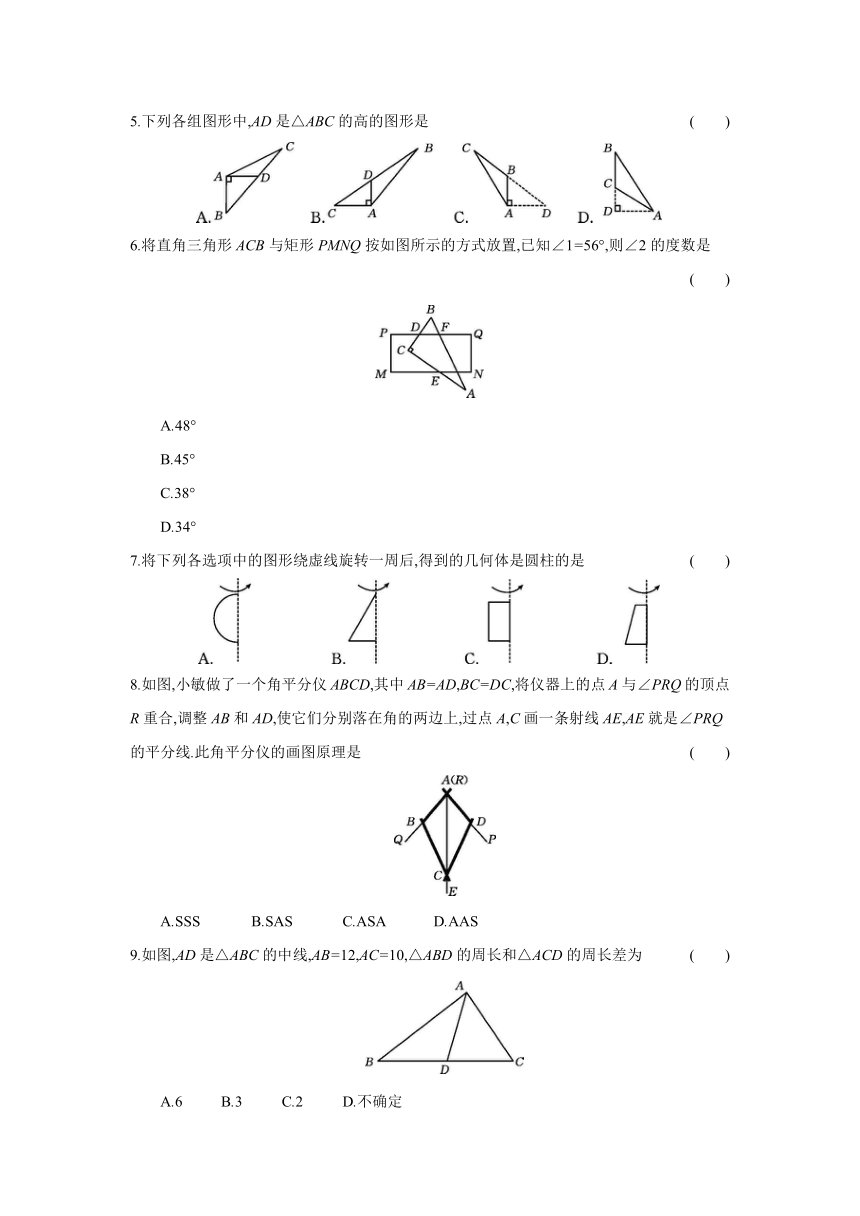
5.下列各组图形中,AD是△ABC的高的图形是 ( )
6.将直角三角形ACB与矩形PMNQ按如图所示的方式放置,已知∠1=56°,则∠2的度数是 ( )
A.48°
B.45°
C.38°
D.34°
7.将下列各选项中的图形绕虚线旋转一周后,得到的几何体是圆柱的是 ( )
8.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是 ( )
A.SSS B.SAS C.ASA D.AAS
9.如图,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为 ( )
A.6 B.3 C.2 D.不确定
10.下列各组数中,能作为直角三角形三边长的是 ( )
A.1,2,3 B.,,
C.1,1, D.3,5,6
11.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4= ( )
A.183 B.87 C.119 D.81
12.随着人们物质生活水平的提高,手机成为了生活中不可缺少的电子产品,手机很方便携带,但是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的哪一个性质 ( )
A.三角形两边之和大于第三边 B.三角形具有稳定性
C.三角形的内角和是180° D.直角三角形两个锐角互余
13.如图,在三角形纸片ABC中,AB=8 cm,BC=6 cm,AC=5 cm,沿过点B的直线折叠这个三角形,使点C落在边AB上的点E处,折痕为BD,则△ADE的周长为 ( )
A.5 cm B.7 cm C.8 cm D.11 cm
14.如图,这是一个正方体,将它沿某些棱展开后,能得到的图形是 ( )
15.定理:三角形的三个内角和等于180°.
已知:如图1,有锐角△ABC.求证:∠A+∠B+∠C=180°.
图1 图2 图3
证法1:如图2,过点C作CD∥AB, ∴∠ACD=∠A(两直线平行,内错角相等). ∵∠B+∠ACB+∠ACD=180°(两直线平行,同旁内角互补), ∴∠A+∠B+∠ACB=180°(等量代换).
证法2:如图3,延长BC到点E, ∴∠ACE=∠A+∠B(三角形的外角等于与它不相邻的两个内角的和). ∵∠ACB+∠ACE=180°(邻补角定义), ∴∠A+∠B+∠ACB=180°(等量代换).
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1严谨地推理证明了该定理
C.证法2简单合理地证明了该定理
D.在证明该定理时不能同时添加证法1与证法2中的辅助线
16.如图,在平面直角坐标系中,点A1,A2,A3,A4…在x轴的正半轴上,点B1,B2,B3…在直线y=x(x≥0)上,若点A1的坐标为(2,0),且△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,则点B10的纵坐标为 ( )
A.3×28 B.3×29 C.×29 D.×210
二、填空题(本大题共3个小题,共10分.17小题2分;18~19小题各4分,每空2分)
17.如图,在△BCD中,若CA平分∠BCD交BD于点A,过点A作AE∥CD交BC于点E,则当AE=5时,CE= .
18.某加工零件标出了部分数据(如图),小明说,这四个数据中有一个标错了,请你完善以下修改方案:若∠A、∠B、∠BCD所标的数据正确,则图中∠D所标的数据应 (填“增大”或“减小”) °.
19.我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,这样的三角形我们称之为“和谐三角形”.如:三个内角分别为 105°,40°,35° 的三角形是“和谐三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM,交ON于点B,以A为端点作射线AC,交OB于点C,∠ABO的度数为 ,若∠ACB=80°,则△AOC (选填“是”或“不是”)“和谐三角形”.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)已知某等腰三角形一边的长为3,另一边的长为6,求这个等腰三角形的周长.
21.(本小题满分9分)如图,在△ABC中,CD是AB边上的高,若AB=10 cm,BC=8 cm,AC=6 cm,求CD的长.
22.(本小题满分9分)如图,点D,E分别在AB,AC上,且AD=AE,AB=AC.
(1)求证:∠B=∠C.
(2)请写出OB与OC的数量关系,并证明.
23.(本小题满分10分)如图1,同学们想测量旗杆的高度,他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学都应用勾股定理提出了解决这个问题的方案.
小明:①测量出绳子垂直落地后还剩余1.5米(如图1);②把绳子拉直,绳子末端在地面上离旗杆底部6米(如图2).
小亮:先在旗杆底端的绳子上打一个结,然后举起绳结拉到如图3所示的点D处.
(1)请你按小明的方案求出旗杆的高度.
(2)已知小亮举起绳结离旗杆6.75米远,则此时绳结离地面多高
24.(本小题满分10分)
(1)如图1,E是等边三角形ABC内一点,若AE=1,BE=2,CE=,求∠AEB的度数.我们求解思路可以是这样:将△ABE绕点B顺时针旋转60°得到△CBD,所以∠AEB=∠BDC,且CD=AE=1,连接ED,可证△BDE是 三角形,从而得到ED= ,又∵CE=,CD=1,根据勾股定理逆定理可得△ 是直角三角形,易得∠EDC=60°,即∠BDC=60°+60°=120°,从而得到∠AEB的度数.
(2)如图2,E是正方形ABCD内的一点,连接AE,BE,CE.若AE=1,BE=2,CE=3,求∠BEA的度数.
25.(本小题满分12分)如图1,在Rt△ABC中,∠ACB=90°,AB=4,∠B=30°,D,E,N分别是BC,AC,AB的中点,连接DE,M是DE的中点,连接CM,CN.
(1)求线段CN与CM的长度.
(2)将△CDE绕顶点C旋转一周,请直接写出点M与点N之间距离的最大值和最小值.
(3)如图2,将图1中的△CDE绕顶点D顺时针旋转60°得到△PDQ,连接CQ,PE,H是PE的中点,连接QH.求证:QH⊥AB.
26.(本小题满分13分)如图1,已知E,F分别是等边三角形ABC的两边AB,AC上的点,且BE=AF,CE,BF交于点O.
(1)求∠BOE的度数.
(2)如图2,延长图1中的CE至点M,使OM=OB,连接AM,BM,运用(1)中的结论证明AM∥BF.
(3)如图3,△ABC与△MBO均为等腰三角形时,其中BM=BO,AB=BC,∠MBO=∠ABC=100°,连接AM,CO,请直接写出AM与CO所在直线构成的锐角的度数.
参考答案
1.D 2.D 3.B 4.C 5.D 6.D 7.C 8.A 9.C 10.C 11.B 12.B 13.B 14.A 15.A
16.C 提示:∵点B1,B2,B3…在直线y=x(x≥0)上,∴∠B1OA1=30°.∵等边△A1B1A2的边长为2,∴等边△A2B2A3的边长OA2的长度为4,等边△A3B3A4的边长OA3的长度为8…等边△A10B10A11的边长OA10的长度为210,∴该等边三角形的高=×210=×29.故选C.
17.5 18.增大;5
19.30°;是
20.解:∵3+3=6,∴该等腰三角形的三边长分别是6,6,3, 4分
∴该等腰三角形的周长=6+6+3=15. 9分
21.解:∵AB=10 cm,BC=8 cm,AC=6 cm,
∴BC2+AC2=AB2,
∴△ACB是以AB为斜边的直角三角形. 3分
∵CD是AB边上的高,
∴AC·BC=AB·CD,
∴CD==4.8 cm. 9分
22.解:(1)证明:∵AE=AD,∠A=∠A,AB=AC,
∴△ABE≌△ACD,
∴∠B=∠C. 4分
(2)OB=OC.
证明:如图,连接BC.
∵AB=AC,
∴∠ABC=∠ACB.
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠ABC-∠ABE=∠ACB-∠ACD,
即∠OBC=∠OCB,
∴OB=OC. 9分
23.解:(1)如题图2,设旗杆的长度为x米,则绳子的长度为(x+1.5)米.
在Rt△ABC中,由勾股定理得x2+62=(x+1.5)2, 2分
解得x=11.25.
故旗杆的高度为11.25米. 4分
(2)由题意可知,BD=BC=11.25米,DE=6.75米.
在Rt△BDE中,由勾股定理得BE2+6.752=11.252,
解得BE=9, 6分
∴EC=BC-BE=11.25-9=2.25米,
∴DF=EC=2.25米.
故绳结离地面2.25米高. 10分
24.解:(1)等边;2;EDC. 3分
(2)如图,将△BAE顺时针旋转90°得到△BCF,连接EF,
∴BF=BE=2,FC=AE=1,∠BEA=∠BFC,
∴在等腰Rt△BEF中,EF===2,且∠BFE=45°. 5分
∵(2)2+12=32,
∴EF2+CF2=EC2,
∴△EFC是直角三角形,
∴∠EFC=90°, 8分
∴∠BFC=45°+90°=135°,
∴∠BEA=∠BFC=135°. 10分
25.解:(1)在Rt△ABC中.∵N是AB的中点,
∴CN=AB=2.
∵D,E分别是BC,AC的中点,∴DE=AB=2.
在Rt△DEC中.∵M是DE的中点,
∴CM=DE=1. 3分
(2)MN的最大值是3,最小值是1. 5分
(3)证明:如图,连接DE,DH.
∵D,E分别是BC,AC的中点,
∴DE∥AB,∴∠CDE=∠B=30°.
由旋转性质得∠CDP=60°,CD=PD且DE=DQ,
∴∠PDE=30°+60°=90°. 7分
∵H是PE的中点,
∴DH=HE,
∴点H在DE的垂直平分线上.
又∵∠CDQ=∠CDP-∠QDP=60°-30°=30°,
∴∠CDQ=∠PDQ,
∴△PDQ≌△CDQ, 10分
∴∠QCD=∠QPD=90°,
∴∠QCD+∠ECD=180°,
∴Q,C,E三点共线,
∴△DQE是等边三角形,
∴QD=QE, 11分
∴点Q在DE的垂直平分线上,即QH垂直平分DE.
∵DE∥AB,
∴QH⊥AB. 12分
26.解:(1)∵△ABC是等边三角形,
∴BC=AB,∠EBC=∠A.
又∵BE=AF,∴△BCE≌△ABF,
∴∠BCE=∠ABF.
∵∠BOE是△BOC的外角,
∴∠BOE=∠OBC+∠BCE=∠OBC+∠ABF,
即∠BOE=∠ABC=60°. 4分
(2)证明:∵OM=OB,∠BOE=60°,
∴△BMO是等边三角形. 5分
又∵△BAC是等边三角形,
∴∠MBO=∠ABC=60°,MB=OB,AB=CB,
∴∠MBA=∠OBC,
∴△AMB≌△COB, 6分
∴∠AMB=∠COB.
又∵∠COB=180°-∠BOE=120°,
∴∠AMB=120°, 7分
∴∠AMO=∠AMB-∠OMB=120°-60°=60°,
∴∠AMO=∠MOB,
∴AM∥BF. 9分
(3)AM与CO所在直线构成的锐角的度数是80°. 13分
提示:如图,延长CO交AM于点N,交AB于点H.
∵∠MBO=∠ABC,
∴∠MBA=∠OBC.
由题意得AB=BC,MB=OB,
∴△MBA≌△OBC,
∴∠MAB=∠OCB,
∴180°-∠MAB-∠AHN=180°-∠OCB-∠BHC,
即∠ANH=∠ABC=100°,
∴∠MNH=180°-100°=80°,
∴AM与CO所在直线构成的锐角的度数是80°.
题号 一 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 线段的中点,线段的和差、角度计算,方位角,余角和(邻)补角,度、分、秒的简单换算.立体图形与平面图形.相交线,垂直的意义及性质,距离(点到线,点到点,垂线段),平行线的性质定理和判定定理及平行于同一条直线的两条直线平行,相关证明,图形的展开与折叠.基本事实:两点确定一条直线,两点之间线段最短、过一点有且只有一条直线与已知直线垂直,尺规作图;三角形的相关概念,内角和定理及推论,三边关系,三角形的全等,等腰(等边)三角形的性质定理和判定定理,直角三角形的性质定理和判定、勾股定理及其逆定理,角平分线性质定理及其逆定理,线段垂直平分线性质定理及其逆定理,定义、命题、定理
一、选择题(本大题共16个小题,共 38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,∠AOD-∠AOC等于 ( )
A.∠AOC B.∠BOC C.∠BOD D.∠COD
2.图中的三角形被木板遮住了一部分,这个三角形是 ( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上都有可能
3.下列几何图形中,不一定是轴对称图形的是 ( )
A.等腰三角形 B.直角三角形
C.矩形 D.等边三角形
4.已知△ABC的三边长分别为a,2,5,那么a的值可以是 ( )
A.2 B.3 C.5 D.7
5.下列各组图形中,AD是△ABC的高的图形是 ( )
6.将直角三角形ACB与矩形PMNQ按如图所示的方式放置,已知∠1=56°,则∠2的度数是 ( )
A.48°
B.45°
C.38°
D.34°
7.将下列各选项中的图形绕虚线旋转一周后,得到的几何体是圆柱的是 ( )
8.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是 ( )
A.SSS B.SAS C.ASA D.AAS
9.如图,AD是△ABC的中线,AB=12,AC=10,△ABD的周长和△ACD的周长差为 ( )
A.6 B.3 C.2 D.不确定
10.下列各组数中,能作为直角三角形三边长的是 ( )
A.1,2,3 B.,,
C.1,1, D.3,5,6
11.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1,S2,S3,S4.若S1=48,S2+S3=135,则S4= ( )
A.183 B.87 C.119 D.81
12.随着人们物质生活水平的提高,手机成为了生活中不可缺少的电子产品,手机很方便携带,但是没有固定的支点,为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的哪一个性质 ( )
A.三角形两边之和大于第三边 B.三角形具有稳定性
C.三角形的内角和是180° D.直角三角形两个锐角互余
13.如图,在三角形纸片ABC中,AB=8 cm,BC=6 cm,AC=5 cm,沿过点B的直线折叠这个三角形,使点C落在边AB上的点E处,折痕为BD,则△ADE的周长为 ( )
A.5 cm B.7 cm C.8 cm D.11 cm
14.如图,这是一个正方体,将它沿某些棱展开后,能得到的图形是 ( )
15.定理:三角形的三个内角和等于180°.
已知:如图1,有锐角△ABC.求证:∠A+∠B+∠C=180°.
图1 图2 图3
证法1:如图2,过点C作CD∥AB, ∴∠ACD=∠A(两直线平行,内错角相等). ∵∠B+∠ACB+∠ACD=180°(两直线平行,同旁内角互补), ∴∠A+∠B+∠ACB=180°(等量代换).
证法2:如图3,延长BC到点E, ∴∠ACE=∠A+∠B(三角形的外角等于与它不相邻的两个内角的和). ∵∠ACB+∠ACE=180°(邻补角定义), ∴∠A+∠B+∠ACB=180°(等量代换).
下列说法正确的是 ( )
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1严谨地推理证明了该定理
C.证法2简单合理地证明了该定理
D.在证明该定理时不能同时添加证法1与证法2中的辅助线
16.如图,在平面直角坐标系中,点A1,A2,A3,A4…在x轴的正半轴上,点B1,B2,B3…在直线y=x(x≥0)上,若点A1的坐标为(2,0),且△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,则点B10的纵坐标为 ( )
A.3×28 B.3×29 C.×29 D.×210
二、填空题(本大题共3个小题,共10分.17小题2分;18~19小题各4分,每空2分)
17.如图,在△BCD中,若CA平分∠BCD交BD于点A,过点A作AE∥CD交BC于点E,则当AE=5时,CE= .
18.某加工零件标出了部分数据(如图),小明说,这四个数据中有一个标错了,请你完善以下修改方案:若∠A、∠B、∠BCD所标的数据正确,则图中∠D所标的数据应 (填“增大”或“减小”) °.
19.我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,这样的三角形我们称之为“和谐三角形”.如:三个内角分别为 105°,40°,35° 的三角形是“和谐三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM,交ON于点B,以A为端点作射线AC,交OB于点C,∠ABO的度数为 ,若∠ACB=80°,则△AOC (选填“是”或“不是”)“和谐三角形”.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)已知某等腰三角形一边的长为3,另一边的长为6,求这个等腰三角形的周长.
21.(本小题满分9分)如图,在△ABC中,CD是AB边上的高,若AB=10 cm,BC=8 cm,AC=6 cm,求CD的长.
22.(本小题满分9分)如图,点D,E分别在AB,AC上,且AD=AE,AB=AC.
(1)求证:∠B=∠C.
(2)请写出OB与OC的数量关系,并证明.
23.(本小题满分10分)如图1,同学们想测量旗杆的高度,他们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.小明和小亮同学都应用勾股定理提出了解决这个问题的方案.
小明:①测量出绳子垂直落地后还剩余1.5米(如图1);②把绳子拉直,绳子末端在地面上离旗杆底部6米(如图2).
小亮:先在旗杆底端的绳子上打一个结,然后举起绳结拉到如图3所示的点D处.
(1)请你按小明的方案求出旗杆的高度.
(2)已知小亮举起绳结离旗杆6.75米远,则此时绳结离地面多高
24.(本小题满分10分)
(1)如图1,E是等边三角形ABC内一点,若AE=1,BE=2,CE=,求∠AEB的度数.我们求解思路可以是这样:将△ABE绕点B顺时针旋转60°得到△CBD,所以∠AEB=∠BDC,且CD=AE=1,连接ED,可证△BDE是 三角形,从而得到ED= ,又∵CE=,CD=1,根据勾股定理逆定理可得△ 是直角三角形,易得∠EDC=60°,即∠BDC=60°+60°=120°,从而得到∠AEB的度数.
(2)如图2,E是正方形ABCD内的一点,连接AE,BE,CE.若AE=1,BE=2,CE=3,求∠BEA的度数.
25.(本小题满分12分)如图1,在Rt△ABC中,∠ACB=90°,AB=4,∠B=30°,D,E,N分别是BC,AC,AB的中点,连接DE,M是DE的中点,连接CM,CN.
(1)求线段CN与CM的长度.
(2)将△CDE绕顶点C旋转一周,请直接写出点M与点N之间距离的最大值和最小值.
(3)如图2,将图1中的△CDE绕顶点D顺时针旋转60°得到△PDQ,连接CQ,PE,H是PE的中点,连接QH.求证:QH⊥AB.
26.(本小题满分13分)如图1,已知E,F分别是等边三角形ABC的两边AB,AC上的点,且BE=AF,CE,BF交于点O.
(1)求∠BOE的度数.
(2)如图2,延长图1中的CE至点M,使OM=OB,连接AM,BM,运用(1)中的结论证明AM∥BF.
(3)如图3,△ABC与△MBO均为等腰三角形时,其中BM=BO,AB=BC,∠MBO=∠ABC=100°,连接AM,CO,请直接写出AM与CO所在直线构成的锐角的度数.
参考答案
1.D 2.D 3.B 4.C 5.D 6.D 7.C 8.A 9.C 10.C 11.B 12.B 13.B 14.A 15.A
16.C 提示:∵点B1,B2,B3…在直线y=x(x≥0)上,∴∠B1OA1=30°.∵等边△A1B1A2的边长为2,∴等边△A2B2A3的边长OA2的长度为4,等边△A3B3A4的边长OA3的长度为8…等边△A10B10A11的边长OA10的长度为210,∴该等边三角形的高=×210=×29.故选C.
17.5 18.增大;5
19.30°;是
20.解:∵3+3=6,∴该等腰三角形的三边长分别是6,6,3, 4分
∴该等腰三角形的周长=6+6+3=15. 9分
21.解:∵AB=10 cm,BC=8 cm,AC=6 cm,
∴BC2+AC2=AB2,
∴△ACB是以AB为斜边的直角三角形. 3分
∵CD是AB边上的高,
∴AC·BC=AB·CD,
∴CD==4.8 cm. 9分
22.解:(1)证明:∵AE=AD,∠A=∠A,AB=AC,
∴△ABE≌△ACD,
∴∠B=∠C. 4分
(2)OB=OC.
证明:如图,连接BC.
∵AB=AC,
∴∠ABC=∠ACB.
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∴∠ABC-∠ABE=∠ACB-∠ACD,
即∠OBC=∠OCB,
∴OB=OC. 9分
23.解:(1)如题图2,设旗杆的长度为x米,则绳子的长度为(x+1.5)米.
在Rt△ABC中,由勾股定理得x2+62=(x+1.5)2, 2分
解得x=11.25.
故旗杆的高度为11.25米. 4分
(2)由题意可知,BD=BC=11.25米,DE=6.75米.
在Rt△BDE中,由勾股定理得BE2+6.752=11.252,
解得BE=9, 6分
∴EC=BC-BE=11.25-9=2.25米,
∴DF=EC=2.25米.
故绳结离地面2.25米高. 10分
24.解:(1)等边;2;EDC. 3分
(2)如图,将△BAE顺时针旋转90°得到△BCF,连接EF,
∴BF=BE=2,FC=AE=1,∠BEA=∠BFC,
∴在等腰Rt△BEF中,EF===2,且∠BFE=45°. 5分
∵(2)2+12=32,
∴EF2+CF2=EC2,
∴△EFC是直角三角形,
∴∠EFC=90°, 8分
∴∠BFC=45°+90°=135°,
∴∠BEA=∠BFC=135°. 10分
25.解:(1)在Rt△ABC中.∵N是AB的中点,
∴CN=AB=2.
∵D,E分别是BC,AC的中点,∴DE=AB=2.
在Rt△DEC中.∵M是DE的中点,
∴CM=DE=1. 3分
(2)MN的最大值是3,最小值是1. 5分
(3)证明:如图,连接DE,DH.
∵D,E分别是BC,AC的中点,
∴DE∥AB,∴∠CDE=∠B=30°.
由旋转性质得∠CDP=60°,CD=PD且DE=DQ,
∴∠PDE=30°+60°=90°. 7分
∵H是PE的中点,
∴DH=HE,
∴点H在DE的垂直平分线上.
又∵∠CDQ=∠CDP-∠QDP=60°-30°=30°,
∴∠CDQ=∠PDQ,
∴△PDQ≌△CDQ, 10分
∴∠QCD=∠QPD=90°,
∴∠QCD+∠ECD=180°,
∴Q,C,E三点共线,
∴△DQE是等边三角形,
∴QD=QE, 11分
∴点Q在DE的垂直平分线上,即QH垂直平分DE.
∵DE∥AB,
∴QH⊥AB. 12分
26.解:(1)∵△ABC是等边三角形,
∴BC=AB,∠EBC=∠A.
又∵BE=AF,∴△BCE≌△ABF,
∴∠BCE=∠ABF.
∵∠BOE是△BOC的外角,
∴∠BOE=∠OBC+∠BCE=∠OBC+∠ABF,
即∠BOE=∠ABC=60°. 4分
(2)证明:∵OM=OB,∠BOE=60°,
∴△BMO是等边三角形. 5分
又∵△BAC是等边三角形,
∴∠MBO=∠ABC=60°,MB=OB,AB=CB,
∴∠MBA=∠OBC,
∴△AMB≌△COB, 6分
∴∠AMB=∠COB.
又∵∠COB=180°-∠BOE=120°,
∴∠AMB=120°, 7分
∴∠AMO=∠AMB-∠OMB=120°-60°=60°,
∴∠AMO=∠MOB,
∴AM∥BF. 9分
(3)AM与CO所在直线构成的锐角的度数是80°. 13分
提示:如图,延长CO交AM于点N,交AB于点H.
∵∠MBO=∠ABC,
∴∠MBA=∠OBC.
由题意得AB=BC,MB=OB,
∴△MBA≌△OBC,
∴∠MAB=∠OCB,
∴180°-∠MAB-∠AHN=180°-∠OCB-∠BHC,
即∠ANH=∠ABC=100°,
∴∠MNH=180°-100°=80°,
∴AM与CO所在直线构成的锐角的度数是80°.
同课章节目录
