2 函数(含答案)2025年中考数学总复习专题练(河北)
文档属性
| 名称 | 2 函数(含答案)2025年中考数学总复习专题练(河北) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 18:33:49 | ||
图片预览


文档简介
2函数
题号 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 函数及图象,平面直角坐标系,正比例函数、一次函数、二次函数、反比例函数的图象、性质及应用;根据一次函数的图象求二元一次方程组的近似解,根据二次函数的图象求一元二次方程的近似解
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在函数y=中,自变量x的取值范围是 ( )
A.x>-3 B.x≥2
C.x>-3且x≥2 D.x≥-3且x≥2
2.已知反比例函数y=-,当x≤-2时,y有 ( )
A.最小值,最小值为2 B.最大值,最大值为2
C.最小值,最小值为-2 D.最大值,最大值为-2
3.对于抛物线y=-2x2+4x+1,下列判断正确的是 ( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(-1,3)
C.对称轴为直线x=-1
D.与x轴的交点坐标为(1+,0)、(1-,0)
4.用图象法解某二元一次方程组时,在同一平面直角坐标系中作出相应的两个一次函数的图象,则所解的二元一次方程组是 ( )
A.
B.
C.
D.
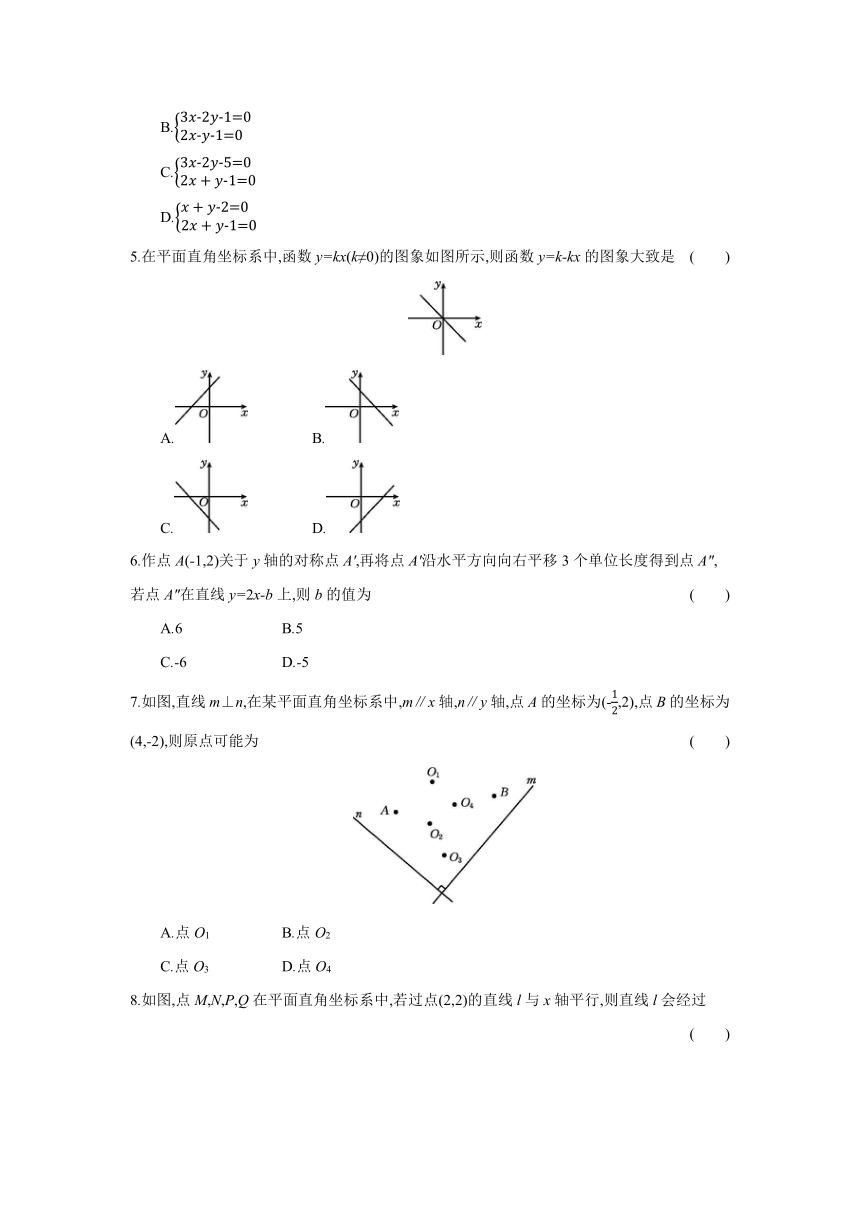
5.在平面直角坐标系中,函数y=kx(k≠0)的图象如图所示,则函数y=k-kx的图象大致是 ( )
A. B.
C. D.
6.作点A(-1,2)关于y轴的对称点A',再将点A'沿水平方向向右平移3个单位长度得到点A″,若点A″在直线y=2x-b上,则b的值为 ( )
A.6 B.5
C.-6 D.-5
7.如图,直线m⊥n,在某平面直角坐标系中,m∥x轴,n∥y轴,点A的坐标为(-,2),点B的坐标为(4,-2),则原点可能为 ( )
A.点O1 B.点O2
C.点O3 D.点O4
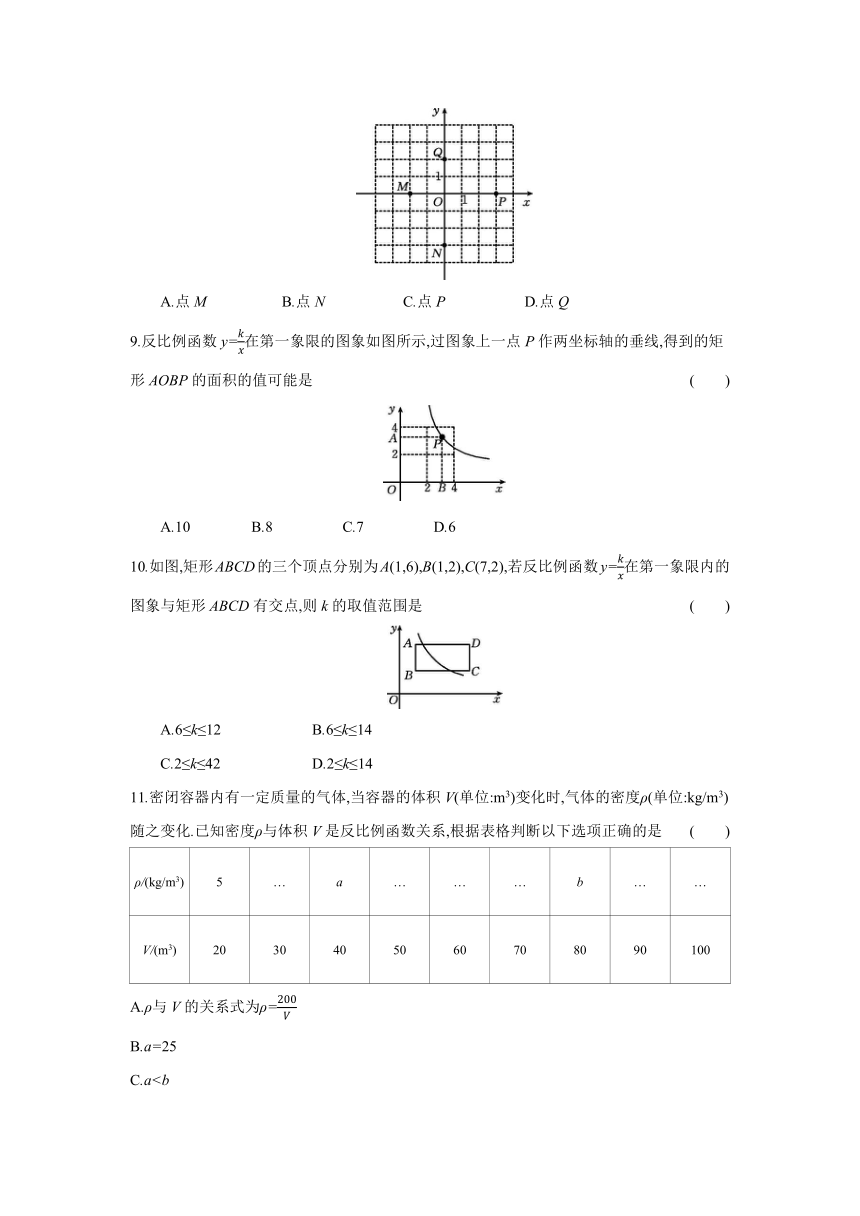
8.如图,点M,N,P,Q在平面直角坐标系中,若过点(2,2)的直线l与x轴平行,则直线l会经过 ( )
A.点M B.点N C.点P D.点Q
9.反比例函数y=在第一象限的图象如图所示,过图象上一点P作两坐标轴的垂线,得到的矩形AOBP的面积的值可能是 ( )
A.10 B.8 C.7 D.6
10.如图,矩形ABCD的三个顶点分别为A(1,6),B(1,2),C(7,2),若反比例函数y=在第一象限内的图象与矩形ABCD有交点,则k的取值范围是 ( )
A.6≤k≤12 B.6≤k≤14
C.2≤k≤42 D.2≤k≤14
11.密闭容器内有一定质量的气体,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,根据表格判断以下选项正确的是 ( )
ρ/(kg/m3) 5 … a … … … b … …
V/(m3) 20 30 40 50 60 70 80 90 100
A.ρ与V的关系式为ρ=
B.a=25
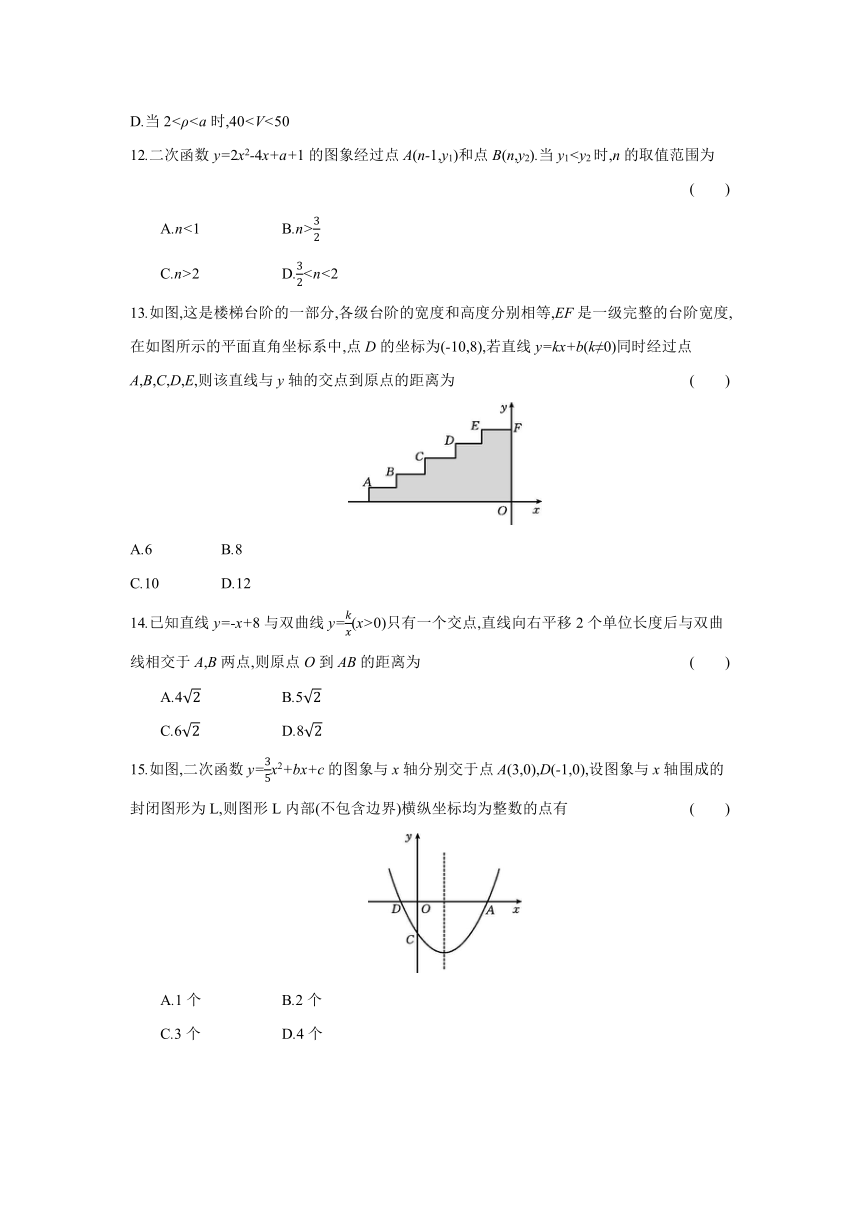
C.aD.当2<ρ12.二次函数y=2x2-4x+a+1的图象经过点A(n-1,y1)和点B(n,y2).当y1A.n<1 B.n>
C.n>2 D.13.如图,这是楼梯台阶的一部分,各级台阶的宽度和高度分别相等,EF是一级完整的台阶宽度,在如图所示的平面直角坐标系中,点D的坐标为(-10,8),若直线y=kx+b(k≠0)同时经过点A,B,C,D,E,则该直线与y轴的交点到原点的距离为 ( )
A.6 B.8
C.10 D.12
14.已知直线y=-x+8与双曲线y=(x>0)只有一个交点,直线向右平移2个单位长度后与双曲线相交于A,B两点,则原点O到AB的距离为 ( )
A.4 B.5
C.6 D.8
15.如图,二次函数y=x2+bx+c的图象与x轴分别交于点A(3,0),D(-1,0),设图象与x轴围成的封闭图形为L,则图形L内部(不包含边界)横纵坐标均为整数的点有 ( )
A.1个 B.2个
C.3个 D.4个
16.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列5个结论:①abc>0;②bA.2个 B.3个
C.4个 D.5个
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17.二次函数y=(x-1)2-的图象如图所示,利用图象可得方程(x-1)2-=0的近似解为 (精确到0.1).
18.如图,在直线l:y=x+1上依次取点A1,A2,A3,A4,…,这些点的横坐标依次是1,2,3,4,…,且这些点与y轴及x轴的垂线构成形如“┐”的图形,这些图形阴影部分的面积分别为S1,S2,S3,….
(1)点A10的坐标为 .
(2)S1+S2+S3+…+S10= .
19.如图,这是壁挂燃气炉工作原理的示意图,其开始工作时的温度是20 ℃,然后按照一次函数关系一直增加到设定的最高温度70 ℃,在此温度下再沿反比例函数关系缓慢下降至待机状态的温度35 ℃,然后在此基础上又沿着一次函数关系一直将温度升至70 ℃,再在此温度下沿着反比例函数关系缓慢下降至35 ℃,如此循环下去.
(1)t的值为 .
(2)如果在0~t分钟内,当温度大于或等于50 ℃时,室内舒适度高,那么维持这个温度范围的持续时间为 分钟.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)如图,一次函数y=-x+6的图象与坐标轴交于A,B两点,求点B的坐标.
21.(本小题满分9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与正比例函数y=-3x的图象交于点P(m,3),与y轴相交于点B(0,2),与x轴相交于点A.
(1)求一次函数解析式.
(2)求△AOP的面积.
22.(本小题满分9分)如图,正比例函数y=kx的图象与反比例函数y=(x>0)的图象经过点A(a,4),B为x轴正半轴上一点,过点B作BD⊥x轴,交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)求a,k的值.
(2)连接AC,如果BD=6,求△ACD的面积.
23.(本小题满分10分)数字经济助力乡村振兴,某电商平台准备销售一批地方特色农产品,该农产品进货价格为每件50元,经过试营销发现,每月的销售量y(件)与每件的售价x(元)之间满足如图所示的函数关系.
(1)求每月的销售量y(件)与每件的售价x(元)之间的函数关系式.(不用写出x的取值范围)
(2)物价部门规定,该农产品每件的利润不允许高于进货价的40%.设销售该农产品每月的总利润为W(元),那么售价定为多少元可获得最大利润 最大利润是多少
24.(本小题满分10分)如图,二次函数y=ax2+bx-3(a≠0)的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.一次函数y=kx+t(k≠0)的图象经过点B,C.
(1)求二次函数的解析式.
(2)根据图象,请直接写出ax2+bx-3>kx+t的x的取值范围.
25.(本小题满分12分)科学课上,同学用自制密度计测量液体的密度.如图,密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=30 cm.
(1)求h关于ρ的函数解析式.
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
26.(本小题满分13分)如图1,抛物线y=ax2+bx+4与y轴交于点C,与x轴交于点A,B,且OA=OC=4OB,点C,D关于该抛物线的对称轴对称,直线l经过点B,D.
(1)求抛物线和直线l的解析式.
(2)若P是直线l上方该抛物线上的一点(不与点D,B重合),当△PBD的面积最大时,求点P的坐标及△PBD的面积最大值.
(3)如图2,线段EF在直线BD上移动,且EF=,设点E的横坐标为m,过点E作y轴的平行线与抛物线交于点P,过点F作y轴的平行线与x轴交于点Q.以点E,F,P,Q为顶点的四边形能否为平行四边形 若能,请你直接写出m的值;若不能,请说明理由.
参考答案
1.B 2.B 3.D 4.A 5.D 6.A 7.B 8.D 9.A 10.C 11.D 12.B 13.D 14.B
15.D
16.A 提示:由抛物线开口向下,可得a<0,抛物线交y轴于正半轴,故知c>0,因为抛物线的对称轴为x=-=1,故知b>0,∴abc<0;故结论①错误;
当x=-1时,y<0,∴y=a-b+c<0,∴b>a+c,故结论②错误;
由抛物线的对称性可得当x=3时,y<0,即9a+3b+c<0,故结论③正确;
∵抛物线开口向下,抛物线y=ax2+bx+c的对称轴是直线x=1,∴当x≥0时,y=ax2+bx+c有最大值,没有最小值,故结论④错误;
由图象可知,y>2时,函数图象上找不到与之对应的x值,∴方程ax2+bx+c=n有实数根的条件是n≤2,故结论⑤正确.
综上所述,正确的有③⑤,共2个,故选A.
17.1.7或0.3
18.(1)(10,11)
(2)130
19.(1)50
(2)20
提示:(1)当25≤x≤t时,设第一次循环过程中反比例函数的表达式为y=,由题意得70=,∴m=1750,∴y=,∴当y=35时,t=50,∴t的值为50.
(2)当0≤x≤25时,设第一次循环过程中一次函数的表达式为y=kx+b,将(0,20),(25,70)代入,得解得∴一次函数的表达式为y=2x+20.当y=50时,则2x+20=50,解得x=15;当y=50,=50,解得x=35,∴在0~t分钟内,当温度大于或等于50 ℃时,室内舒适度高,维持这个温度范围的持续时间为35-15=20(分钟).
20.解:令y=0,即-x+6=0,解得x=8,
∴B(8,0). 9分
21.解:(1)在y=-3x中,令y=3,解得x=-1,∴P(-1,3).
∵点P(-1,3),点B(0,2)在y=kx+b上,
∴解得
∴一次函数解析式为y=-x+2. 3分
(2)在y=-x+2中,令y=0,∴-x+2=0,解得x=2,∴A(2,0).
又∵点P(-1,3),O(0,0),∴S△AOP=×2×3=3. 9分
22.解:(1)在y=中,令y=4,解得a=2, 1分
∴A(2,4).
∵点A(2,4)在y=kx上,∴2k=4,解得k=2. 3分
(2)令B(m,0).∵BD⊥x轴,∴D(m,2m),
∴BD=2m=6,∴m=3,∴D(3,6). 4分
在y=中,令x=3,则y=,∴C(3,),
∴S△ACD=×(6-)×(3-2)=. 9分
23.解:(1)设每月的销售量y(件)与每件的售价x(元)之间的函数关系式为y=kx+b,
∴解得
∴y=-2x+300. 3分
(2)∵农产品每件的利润不允许高于进货价的40%,
∴x-50≤50×40%,
∴x≤70. 4分
W=(x-50)×(-2x+300)=-2(x-100)2+5000. 6分
∵-2<0且x≤70,
∴当x=70时,Wmax=-2×(70-100)2+5000=3200(元),
即当售价定为70元时,可获得最大利润,最大利润是3200元. 10分
24.解:(1)在y=ax2+bx-3中,令x=0,则y=-3,
∴C(0,-3),∴OC=3.
∵BO=OC=3OA,
∴BO=3,OA=1,∴B(3,0),A(-1,0). 2分
∵点B(3,0),A(-1,0)在二次函数y=ax2+bx-3的图象上,
∴解得
∴y=x2-2x-3. 5分
(2)x<0或x>3. 10分
25.解:(1)设h关于ρ的函数解析式为h=,
把ρ=1,h=30代入解析式,得k=1×30=30,
∴h关于ρ的函数解析式为h=. 5分
(2)把h=25代入h=,得25=,
解得ρ=1.2.
答:该液体的密度ρ为1.2 g/cm3. 12分
26.解:(1)在y=ax2+bx+4中,令x=0,则y=4,
∴C(0,4),OC=4.
∵OA=OC=4OB,
∴OB=1,OA=4,∴B(1,0),A(-4,0).
∵点B(1,0),A(-4,0)在抛物线y=ax2+bx+4上,
∴解得
∴抛物线的解析式为y=-x2-3x+4. 2分
抛物线对称轴为直线x=-=-=-.
∵点C,D关于该抛物线的对称轴对称,∴D(-3,4).
设直线l的解析式为y=kx+n,
∴解得
∴直线l的解析式为y=-x+1. 4分
(2)如图1,过点P作PH⊥x轴交BD于点H,连接PD,PB.
设点P(c,-c2-3c+4),H(c,-c+1),-3S△PBD=S△PDH+S△PBH=×PH×|xB-xD|=×[(-c2-3c+4-(-c+1)]×|1-(-3)|
=-2c2-4c+6=-2(c+1)2+8. 6分
∵-3∴当c=-1时,Smax=-2×(-1+1)2+8=8.
即当点P(-1,6)时,△PBD的面积取最大值8. 9分
(3)m1=,m2=,m3=,m4=. 13分
提示:∵D(-3,4),B(1,0),∴∠DBA=45°.
∵EF=,∴xF-xE=1,
点E(m,-m+1),则点P(m,-m2-3m+4),F(m+1,-m),Q(m+1,0),
PE=|-m2-3m+4-(-m+1)|=|-m2-2m+3|,FQ=|-m-0|=|-m|.
∵以E,F,P,Q为顶点的四边形为平行四边形,
∴PE∥FQ,PE=FQ,
∴|-m2-2m+3|=|-m|,
∴-m2-2m+3=-m(如图2,图3)或-m2-2m+3=m(如图4,图5),
解得m1=,m2=或m3=,m4=.
题号 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 函数及图象,平面直角坐标系,正比例函数、一次函数、二次函数、反比例函数的图象、性质及应用;根据一次函数的图象求二元一次方程组的近似解,根据二次函数的图象求一元二次方程的近似解
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在函数y=中,自变量x的取值范围是 ( )
A.x>-3 B.x≥2
C.x>-3且x≥2 D.x≥-3且x≥2
2.已知反比例函数y=-,当x≤-2时,y有 ( )
A.最小值,最小值为2 B.最大值,最大值为2
C.最小值,最小值为-2 D.最大值,最大值为-2
3.对于抛物线y=-2x2+4x+1,下列判断正确的是 ( )
A.抛物线的开口向上
B.抛物线的顶点坐标是(-1,3)
C.对称轴为直线x=-1
D.与x轴的交点坐标为(1+,0)、(1-,0)
4.用图象法解某二元一次方程组时,在同一平面直角坐标系中作出相应的两个一次函数的图象,则所解的二元一次方程组是 ( )
A.
B.
C.
D.
5.在平面直角坐标系中,函数y=kx(k≠0)的图象如图所示,则函数y=k-kx的图象大致是 ( )
A. B.
C. D.
6.作点A(-1,2)关于y轴的对称点A',再将点A'沿水平方向向右平移3个单位长度得到点A″,若点A″在直线y=2x-b上,则b的值为 ( )
A.6 B.5
C.-6 D.-5
7.如图,直线m⊥n,在某平面直角坐标系中,m∥x轴,n∥y轴,点A的坐标为(-,2),点B的坐标为(4,-2),则原点可能为 ( )
A.点O1 B.点O2
C.点O3 D.点O4
8.如图,点M,N,P,Q在平面直角坐标系中,若过点(2,2)的直线l与x轴平行,则直线l会经过 ( )
A.点M B.点N C.点P D.点Q
9.反比例函数y=在第一象限的图象如图所示,过图象上一点P作两坐标轴的垂线,得到的矩形AOBP的面积的值可能是 ( )
A.10 B.8 C.7 D.6
10.如图,矩形ABCD的三个顶点分别为A(1,6),B(1,2),C(7,2),若反比例函数y=在第一象限内的图象与矩形ABCD有交点,则k的取值范围是 ( )
A.6≤k≤12 B.6≤k≤14
C.2≤k≤42 D.2≤k≤14
11.密闭容器内有一定质量的气体,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化.已知密度ρ与体积V是反比例函数关系,根据表格判断以下选项正确的是 ( )
ρ/(kg/m3) 5 … a … … … b … …
V/(m3) 20 30 40 50 60 70 80 90 100
A.ρ与V的关系式为ρ=
B.a=25
C.a
C.n>2 D.
A.6 B.8
C.10 D.12
14.已知直线y=-x+8与双曲线y=(x>0)只有一个交点,直线向右平移2个单位长度后与双曲线相交于A,B两点,则原点O到AB的距离为 ( )
A.4 B.5
C.6 D.8
15.如图,二次函数y=x2+bx+c的图象与x轴分别交于点A(3,0),D(-1,0),设图象与x轴围成的封闭图形为L,则图形L内部(不包含边界)横纵坐标均为整数的点有 ( )
A.1个 B.2个
C.3个 D.4个
16.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列5个结论:①abc>0;②b
C.4个 D.5个
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17.二次函数y=(x-1)2-的图象如图所示,利用图象可得方程(x-1)2-=0的近似解为 (精确到0.1).
18.如图,在直线l:y=x+1上依次取点A1,A2,A3,A4,…,这些点的横坐标依次是1,2,3,4,…,且这些点与y轴及x轴的垂线构成形如“┐”的图形,这些图形阴影部分的面积分别为S1,S2,S3,….
(1)点A10的坐标为 .
(2)S1+S2+S3+…+S10= .
19.如图,这是壁挂燃气炉工作原理的示意图,其开始工作时的温度是20 ℃,然后按照一次函数关系一直增加到设定的最高温度70 ℃,在此温度下再沿反比例函数关系缓慢下降至待机状态的温度35 ℃,然后在此基础上又沿着一次函数关系一直将温度升至70 ℃,再在此温度下沿着反比例函数关系缓慢下降至35 ℃,如此循环下去.
(1)t的值为 .
(2)如果在0~t分钟内,当温度大于或等于50 ℃时,室内舒适度高,那么维持这个温度范围的持续时间为 分钟.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)如图,一次函数y=-x+6的图象与坐标轴交于A,B两点,求点B的坐标.
21.(本小题满分9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与正比例函数y=-3x的图象交于点P(m,3),与y轴相交于点B(0,2),与x轴相交于点A.
(1)求一次函数解析式.
(2)求△AOP的面积.
22.(本小题满分9分)如图,正比例函数y=kx的图象与反比例函数y=(x>0)的图象经过点A(a,4),B为x轴正半轴上一点,过点B作BD⊥x轴,交反比例函数的图象于点C,交正比例函数的图象于点D.
(1)求a,k的值.
(2)连接AC,如果BD=6,求△ACD的面积.
23.(本小题满分10分)数字经济助力乡村振兴,某电商平台准备销售一批地方特色农产品,该农产品进货价格为每件50元,经过试营销发现,每月的销售量y(件)与每件的售价x(元)之间满足如图所示的函数关系.
(1)求每月的销售量y(件)与每件的售价x(元)之间的函数关系式.(不用写出x的取值范围)
(2)物价部门规定,该农产品每件的利润不允许高于进货价的40%.设销售该农产品每月的总利润为W(元),那么售价定为多少元可获得最大利润 最大利润是多少
24.(本小题满分10分)如图,二次函数y=ax2+bx-3(a≠0)的图象与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.一次函数y=kx+t(k≠0)的图象经过点B,C.
(1)求二次函数的解析式.
(2)根据图象,请直接写出ax2+bx-3>kx+t的x的取值范围.
25.(本小题满分12分)科学课上,同学用自制密度计测量液体的密度.如图,密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=30 cm.
(1)求h关于ρ的函数解析式.
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
26.(本小题满分13分)如图1,抛物线y=ax2+bx+4与y轴交于点C,与x轴交于点A,B,且OA=OC=4OB,点C,D关于该抛物线的对称轴对称,直线l经过点B,D.
(1)求抛物线和直线l的解析式.
(2)若P是直线l上方该抛物线上的一点(不与点D,B重合),当△PBD的面积最大时,求点P的坐标及△PBD的面积最大值.
(3)如图2,线段EF在直线BD上移动,且EF=,设点E的横坐标为m,过点E作y轴的平行线与抛物线交于点P,过点F作y轴的平行线与x轴交于点Q.以点E,F,P,Q为顶点的四边形能否为平行四边形 若能,请你直接写出m的值;若不能,请说明理由.
参考答案
1.B 2.B 3.D 4.A 5.D 6.A 7.B 8.D 9.A 10.C 11.D 12.B 13.D 14.B
15.D
16.A 提示:由抛物线开口向下,可得a<0,抛物线交y轴于正半轴,故知c>0,因为抛物线的对称轴为x=-=1,故知b>0,∴abc<0;故结论①错误;
当x=-1时,y<0,∴y=a-b+c<0,∴b>a+c,故结论②错误;
由抛物线的对称性可得当x=3时,y<0,即9a+3b+c<0,故结论③正确;
∵抛物线开口向下,抛物线y=ax2+bx+c的对称轴是直线x=1,∴当x≥0时,y=ax2+bx+c有最大值,没有最小值,故结论④错误;
由图象可知,y>2时,函数图象上找不到与之对应的x值,∴方程ax2+bx+c=n有实数根的条件是n≤2,故结论⑤正确.
综上所述,正确的有③⑤,共2个,故选A.
17.1.7或0.3
18.(1)(10,11)
(2)130
19.(1)50
(2)20
提示:(1)当25≤x≤t时,设第一次循环过程中反比例函数的表达式为y=,由题意得70=,∴m=1750,∴y=,∴当y=35时,t=50,∴t的值为50.
(2)当0≤x≤25时,设第一次循环过程中一次函数的表达式为y=kx+b,将(0,20),(25,70)代入,得解得∴一次函数的表达式为y=2x+20.当y=50时,则2x+20=50,解得x=15;当y=50,=50,解得x=35,∴在0~t分钟内,当温度大于或等于50 ℃时,室内舒适度高,维持这个温度范围的持续时间为35-15=20(分钟).
20.解:令y=0,即-x+6=0,解得x=8,
∴B(8,0). 9分
21.解:(1)在y=-3x中,令y=3,解得x=-1,∴P(-1,3).
∵点P(-1,3),点B(0,2)在y=kx+b上,
∴解得
∴一次函数解析式为y=-x+2. 3分
(2)在y=-x+2中,令y=0,∴-x+2=0,解得x=2,∴A(2,0).
又∵点P(-1,3),O(0,0),∴S△AOP=×2×3=3. 9分
22.解:(1)在y=中,令y=4,解得a=2, 1分
∴A(2,4).
∵点A(2,4)在y=kx上,∴2k=4,解得k=2. 3分
(2)令B(m,0).∵BD⊥x轴,∴D(m,2m),
∴BD=2m=6,∴m=3,∴D(3,6). 4分
在y=中,令x=3,则y=,∴C(3,),
∴S△ACD=×(6-)×(3-2)=. 9分
23.解:(1)设每月的销售量y(件)与每件的售价x(元)之间的函数关系式为y=kx+b,
∴解得
∴y=-2x+300. 3分
(2)∵农产品每件的利润不允许高于进货价的40%,
∴x-50≤50×40%,
∴x≤70. 4分
W=(x-50)×(-2x+300)=-2(x-100)2+5000. 6分
∵-2<0且x≤70,
∴当x=70时,Wmax=-2×(70-100)2+5000=3200(元),
即当售价定为70元时,可获得最大利润,最大利润是3200元. 10分
24.解:(1)在y=ax2+bx-3中,令x=0,则y=-3,
∴C(0,-3),∴OC=3.
∵BO=OC=3OA,
∴BO=3,OA=1,∴B(3,0),A(-1,0). 2分
∵点B(3,0),A(-1,0)在二次函数y=ax2+bx-3的图象上,
∴解得
∴y=x2-2x-3. 5分
(2)x<0或x>3. 10分
25.解:(1)设h关于ρ的函数解析式为h=,
把ρ=1,h=30代入解析式,得k=1×30=30,
∴h关于ρ的函数解析式为h=. 5分
(2)把h=25代入h=,得25=,
解得ρ=1.2.
答:该液体的密度ρ为1.2 g/cm3. 12分
26.解:(1)在y=ax2+bx+4中,令x=0,则y=4,
∴C(0,4),OC=4.
∵OA=OC=4OB,
∴OB=1,OA=4,∴B(1,0),A(-4,0).
∵点B(1,0),A(-4,0)在抛物线y=ax2+bx+4上,
∴解得
∴抛物线的解析式为y=-x2-3x+4. 2分
抛物线对称轴为直线x=-=-=-.
∵点C,D关于该抛物线的对称轴对称,∴D(-3,4).
设直线l的解析式为y=kx+n,
∴解得
∴直线l的解析式为y=-x+1. 4分
(2)如图1,过点P作PH⊥x轴交BD于点H,连接PD,PB.
设点P(c,-c2-3c+4),H(c,-c+1),-3
=-2c2-4c+6=-2(c+1)2+8. 6分
∵-3
即当点P(-1,6)时,△PBD的面积取最大值8. 9分
(3)m1=,m2=,m3=,m4=. 13分
提示:∵D(-3,4),B(1,0),∴∠DBA=45°.
∵EF=,∴xF-xE=1,
点E(m,-m+1),则点P(m,-m2-3m+4),F(m+1,-m),Q(m+1,0),
PE=|-m2-3m+4-(-m+1)|=|-m2-2m+3|,FQ=|-m-0|=|-m|.
∵以E,F,P,Q为顶点的四边形为平行四边形,
∴PE∥FQ,PE=FQ,
∴|-m2-2m+3|=|-m|,
∴-m2-2m+3=-m(如图2,图3)或-m2-2m+3=m(如图4,图5),
解得m1=,m2=或m3=,m4=.
同课章节目录
