5 圆 (含答案)2025年中考数学总复习专题练(河北)
文档属性
| 名称 | 5 圆 (含答案)2025年中考数学总复习专题练(河北) |

|
|
| 格式 | docx | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览



文档简介
5 圆
题号 一 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 圆的有关性质(圆周角,圆心角,垂径定理,内切圆,外接圆,圆内接四边形对角互补),点与圆、直线与圆的位置关系,与圆有关的计算(弧长和扇形面积,圆锥的侧、全面积),正多边形与圆,三角形的外心和内心
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是 ( )
A.直径不是弦
B.圆既是轴对称图形又是中心对称图形
C.任意三点确定一个圆
D.长度相等的弧是等弧
2.如图,用直角曲尺检查制作成半圆形的工件,则合格的工件是 ( )
3.下列图形中的角,是圆心角的是 ( )
4.如图,AB是☉O的直径,点C,D在☉O上,若∠CDB=35°,则∠CBA的度数为 ( )
A.25°
B.35°
C.45°
D.55°
5.如图,在△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为 ( )
A.80°
B.100°
C.130°
D.160°
6.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦AB长为4 m,轮子的吃水深度CD为1 m,则该桨轮船的轮子直径为 ( )
A.3 m
B.4 m
C.5 m
D.6 m
7.如图,∠DCE是☉O内接四边形ABCD的一个外角,若∠BOD=140°,则∠DCE的大小为 ( )
A.50°
B.60°
C.70°
D.80°
8.如图,四边形OABC为菱形,点B,C在以点O为圆心的上,若OA=2 cm,∠1=∠2,则的长为 ( )
A. cm
B. cm
C. cm
D. cm
9.若将一个圆心角为120°,半径为6的扇形纸片围成一个圆锥,则该圆锥的底面圆的半径为 ( )
A.1 B.2 C.3 D.4
10.图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB的长分别为半径,圆心角∠O=120°形成的扇面,若OA=3 m,OB=1.5 m,则阴影部分的面积为 ( )
A.4.25π m2 B.3.25π m2 C.3π m2 D.2.25π m2
11.如图,在扇形AOB中,点P在OA上,连接PB,将△OBP沿PB折叠得到△O1BP. 若∠O=70°,且BO1与所在的圆相切于点B,则∠APO1= ( )
A.40° B.50°
C.60° D.70°
12.如图,在6×6的正方形网格中(小正方形的边长为1,小正方形的顶点称为格点),有5个格点M,N,O,P,Q,以点O为圆心,为半径作圆,则在☉O外的点是 ( )
A.P
B.Q
C.M
D.N
13.在一次海事活动中,☉O所在区域是活动区域,其中弦AB与优弧AB所围成的区域是声呐需要探测的区域.现在A处安装一台声呐设备,其探测区域如图1阴影所示,再在B处安装一台同型号声呐设备,A,B两处同时开启声呐设备,恰好能完成所有区域的探测,如图2阴影所示.
如图3,现将声呐设备放置位置改为☉O上D,E,F点,设计三个方案:①在D点放两台该型号的声呐设备
②在D点、E点分别放一台该型号的声呐设备
③在F点放两台该型号的声呐设备
若能完成所有区域的探测,则正确的方案是 ( )
A.①③ B.①②③ C.②③ D.①②
14.如图,在平面直角坐标系xOy中,正六边形OABCDE的边长是2,点E,B分别在x轴,y轴上,则它的内切圆的圆心M的坐标是 ( )
A.(1,)
B.(1,2)
C.(2,)
D.(1,2)
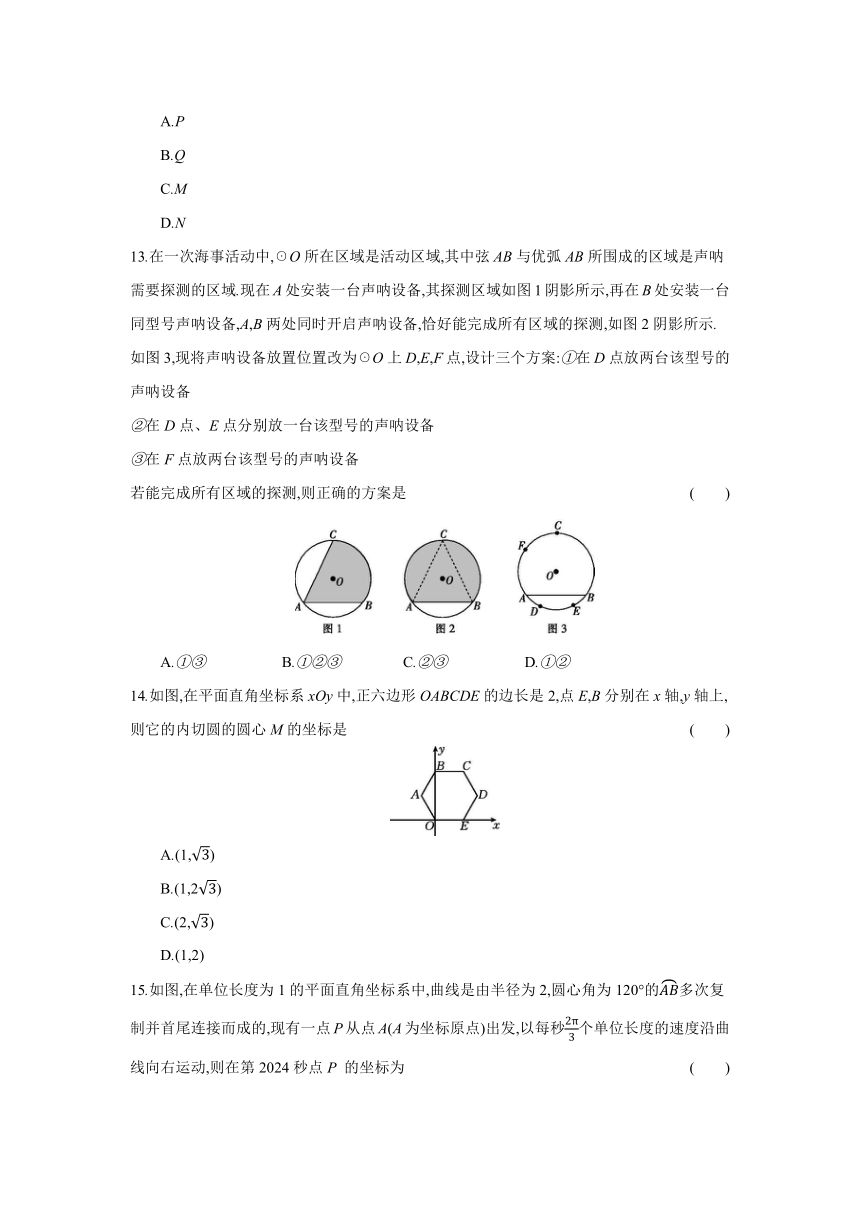
15.如图,在单位长度为1的平面直角坐标系中,曲线是由半径为2,圆心角为120°的多次复制并首尾连接而成的,现有一点P从点A(A为坐标原点)出发,以每秒个单位长度的速度沿曲线向右运动,则在第2024秒点P 的坐标为 ( )
A.(1012,0) B.(2024,0)
C.(1012,0) D.(2024,0)
16.如图,点C在以AB为直径的半圆O上,AB=8,∠CBA=30°,点D在线段AB(不与点A,B重合)上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.有下列结论:
①CE=CF;②∠F=30°;③线段EF的长的最小值为4;④当AD=2时,EF与半圆O相切.
其中正确的个数是 ( )
A.1
B.2
C.3
D.4
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
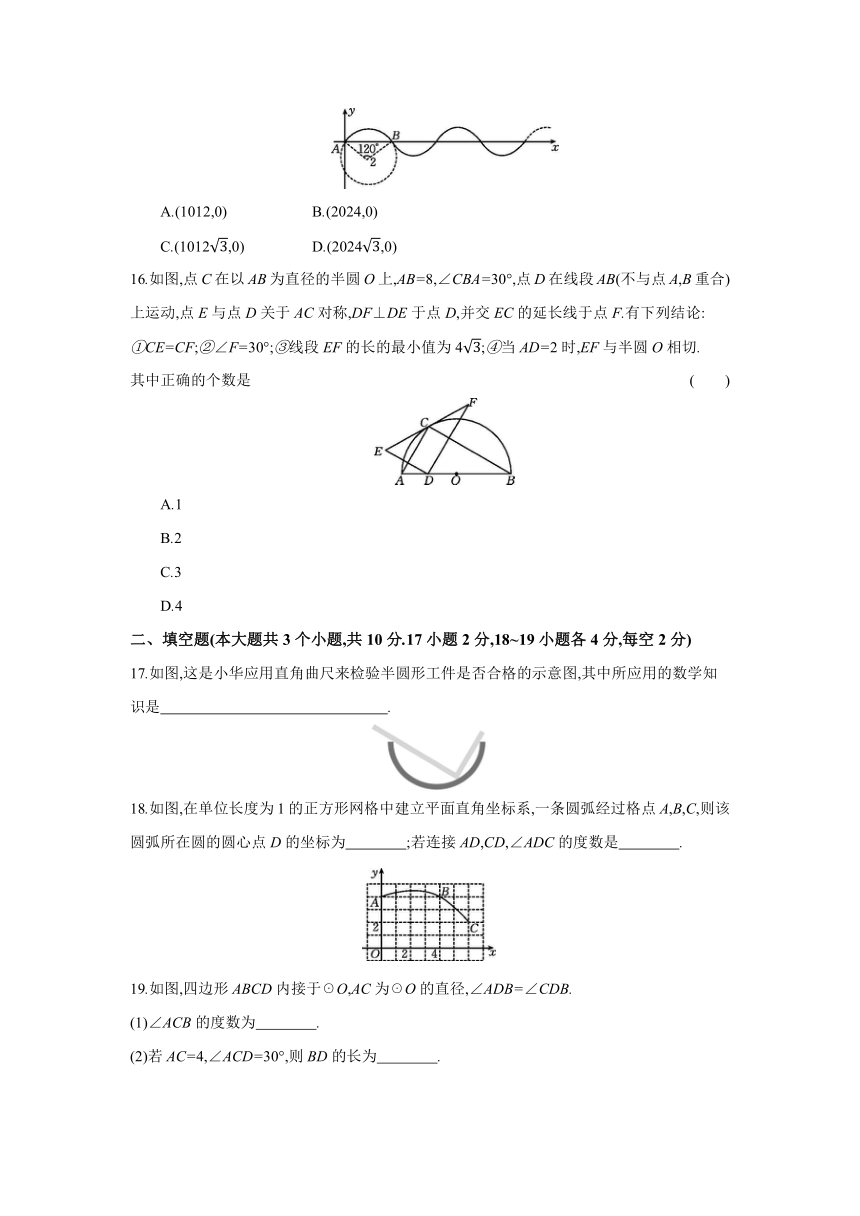
17.如图,这是小华应用直角曲尺来检验半圆形工件是否合格的示意图,其中所应用的数学知识是 .
18.如图,在单位长度为1的正方形网格中建立平面直角坐标系,一条圆弧经过格点A,B,C,则该圆弧所在圆的圆心点D的坐标为 ;若连接AD,CD,∠ADC的度数是 .
19.如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)∠ACB的度数为 .
(2)若AC=4,∠ACD=30°,则BD的长为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)如图,扇形AOB的圆心角为120°,半径OA为4 cm,求扇形AOB的弧长和面积.
21.(本小题满分9分)如图,这是一个粮仓,底面直径为8 m,粮仓顶部顶点到底面的垂直距离为9 m,粮仓下半部分的高为6 m,观察并回答下列问题.
(1)将下面的图形分别绕虚线旋转一周,能形成粮仓的是 (填字母).
(2)求出该粮仓的容积(计算结果保留π).
22.(本小题满分9分)抖空竹在我国有着悠久的历史,是国家级非物质文化遗产之一.如图1,为弘扬传统文化,某校将抖空竹列入了体育课程.在学习了圆之后,数学兴趣小组的同学们对抖空竹进行了探究,示意图如图2所示.已知绳AC,BD分别与空竹☉O相切于点C,D,且AC=BD,连接左右两个绳柄A,B,AB经过圆心O,交☉O于点E,F.
(1)求证:AE=BF.
(2)若AE=4 cm,AC=8 cm,求两个绳柄之间的距离AB.
图1 图2
23.(本小题满分10分)如图,AB是☉O的直径,BC是☉O的弦,过点C作☉O的切线交BA的延长线于点G,D为切线上一点,DE⊥AB于点E,交BC于点F.
(1)求证:CD=DF.
(2)若C为DG的中点,CD=5,cos D=,求BE的长.
24.(本小题满分10分)已知D为☉O上一点,过点D的切线交弦AB的延长线于点C,连接AD,BD.
(1)如图1,当弦AB为直径时,直接写出∠CDB与∠CAD的数量关系: .
(2)如图2,当AB为非直径时,(1)中的结论还成立吗 若成立,写出证明过程;若不成立,请说明理由.
(3)如图2,BC=4,AB=8,求CD的长.
图1 图2
25.(本小题满分12分)如图,在△OAB中,OA=OB,∠A=30°,☉O与AB相切于点D,交OA于点E,交OB于点F,延长AO交☉O于点C,连接BC.
(1)求证:BC是☉O的切线.
(2)连接OD,DF,CF,判断四边形CODF的形状,并说明理由.
(3)若AE=2,求阴影部分的面积.
26.(本小题满分13分)问题提出
(1)如图1,在等腰Rt△ABC中,∠ACB=90°,D是AB边上一点,以CD为腰作等腰Rt△CDE,且∠DCE=90°,连接BE,则AD与BE的数量关系是 ,位置关系是 .
问题探究
(2)如图2,AB是半圆O的直径,C,D是半圆O上的两点,且AC=BC,BD=2,AD=6,连接CD,求CD的长.
问题解决
(3)图3是某公园的一个面积为64π m2的圆形广场示意图,点O为圆心.公园开发部门计划在该广场内设计一个四边形运动区域ABDC,连接BC,AD,其中等边△ABC为球类运动区域,△BCD为散步区域,设AD的长为x,四边形ABDC的面积为S.
①求S与x之间的函数关系式.
②按照设计要求,为了让人们有更大的运动区域,四边形ABDC的面积越大越好,求四边形运动区域ABDC面积的最大值.
图1 图2 图3
参考答案
1.B 2.D 3.C 4.D 5.C 6.C 7.C 8.C 9.B 10.D 11.B 12.A 13.D 14.A 15.D
16.C 提示:①如图,连接CD,
∵点E与点D关于AC对称,∴CD=CE,∴∠E=∠CDE.
∵DF⊥DE,∴∠EDF=90°,
∴∠E+∠F=90°,∠CDE+∠CDF=90°,
∴∠F=∠CDF,
∴CD=CF,∴CE=CF,故①正确.
②∵点E与点D关于AC对称,
∴DE⊥AC.
∵AB是半圆O的直径,
∴∠ACB=90°,∴BC⊥AC,
∴DE∥BC,
∴DF⊥BC.
若∠F=30°,则∠CDF=30°,
∴∠BCD=60°,
∴∠CDB=90°,
∴只有当CD⊥AB时,∠F=30°,故②不正确.
③∵CD=CE=CF,∴EF=2CD,
要使EF的长最小,则CD的长也要最小.
根据“垂线段最短”,∴CD的长最小时,CD⊥AB.
∵∠ACB=90°,AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4.
∵CD⊥AB,∠CBA=30°,
∴CD=BC=2,
∴EF=2CD=4,
∴EF的长的最小值为4,故③正确.
④当AD=2时,如图,连接OC,
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形,
∴CA=CO.
∵AO=4,AD=2,∴OD=2,
∴AD=OD,
∴∠OCD=∠DCA=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA=30°,
∴∠OCE=90°,∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆O相切,故④正确.
故选C.
17.直径所对的圆周角为直角 18.(2,0);90° 19.(1)45° (2)+
20.解:扇形AOB的弧长l==(cm), 4分
扇形AOB的面积S==(cm2). 9分
21.解:(1)D. 4分
(2)粮仓的容积=V圆柱+V圆锥
=π×()2×6+π×()2×(9-6)
=96π+16π
=112π(m3).
答:该粮仓的容积为112π m3. 9分
22.解:(1)证明:如图,连接OC,OD.
∵AC,BD分别与空竹☉O相切于点C,D,
∴∠OCA=∠ODB=90°.
在△OCA和△ODB中,
∴△OCA≌△ODB(SAS),
∴OA=OB.
∵OE=OF,
∴OA-OE=OB-OF,即AE=BF. 4分
(2)设☉O的半径为r cm,
在Rt△AOC中,AC2+OC2=OA2,
∴82+r2=(r+4)2,
解得r=6,
∴OA=6+4=10 cm,
∴AB=2OA=20 cm. 9分
23.解:(1)证明:如图,连接OC.
∵OC=OB,
∴∠OCB=∠B.
∵CD是☉O的切线,
∴∠OCD=90°,
∴∠OCB+∠BCD=90°.
∵DE⊥AB,
∴∠B+∠BFE=90°,
∴∠BCD=∠BFE.
∵∠BFE=∠CFD,
∴∠BCD=∠CFD,
∴CD=DF. 4分
(2)∵C为DG的中点,CD=5,
∴DG=2CD=10,CG=5.
∵DE⊥AB,
∴cos D==,
∴DE=6,EG===8.
∵∠G=∠G,∠OCG=∠DEG=90°,
∴△OCG∽△DEG,
∴==,即==,
∴OG=,OC=,
∴OE=EG-OG=8-=.
∵OB=OC=,
∴BE=OB-OE=-=2. 10分
24.解:(1)∠CDB=∠CAD. 2分
(2)(1)中的结论还成立. 3分
证明:如图,过点B作直径BE,连接DE,OD.
∵CD是☉O的切线,
∴OD⊥CD,
∴∠CDO=90°,
∴∠CDB+∠ODB=90°.
∵BE为☉O的直径,
∴∠EDB=90°,
∴∠ODE+∠ODB=90°,
∴∠CDB=∠ODE.
∵OE=OD,
∴∠E=∠ODE,
∴∠CDB=∠E.
∵=,
∴∠CAD=∠E,
∴∠CDB=∠CAD. 7分
(3)∵∠CDB=∠A,∠DCB=∠ACD,
∴△CBD∽△CDA,
∴=,即=,
∴CD=4. 10分
25.解:(1)证明:如图1,连接OD.
图1
∵OA=OB,∠A=30°,
∴∠AOB=120°,∴∠COB=60°.
∵☉O与AB相切,
∴OD⊥AB,
∴OD平分∠AOB,
∴∠AOD=∠DOB=60°.
在△BOD和△BOC中,
∵OD=OC,∠BOD=∠BOC=60°,OB=OB,
∴△BOD≌△BOC,
∴∠OCB=∠ODB=90°,
∴BC是☉O的切线. 4分
(2)四边形CODF为菱形. 6分
理由:如图2,由(1)知∠COF=∠DOF=60°,OC=OF=OD,
图2
∴△OCF与△ODF都是等边三角形,
∴OC=CF=DF=OD,
∴四边形CODF为菱形. 8分
(3)由(1)知OD⊥AB.
设☉O的半径为r,
∵∠A=30°,OD⊥AB,
∴OA=2OD=2r.
∵AE=2,
∴r+2=2r,
∴r=2.
在Rt△OAD中,AD=OAcos 30°=4×=2,∠AOD=60°,
∴S阴影部分=S△OAD-S扇形DOE=×2×2-=2-. 12分
26.解:(1)相等;垂直. 2分
提示:∵在等腰Rt△ABC中,∠ACB=90°,
∴∠A=∠ABC=45°.
∵∠DCE=∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE.
∵AC=BC,DC=EC,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CBE=∠A=45°,
∴∠DBE=∠ABC+∠CBE=90°,
∴AD⊥BE.
(2)如图1,过点C作CE⊥CD交AD于点E.
图1
∵AB是半圆O的直径,
∴∠ACB=90°.
∵BC=AC,
∴∠ABC=45°,
∴∠CDA=45°.
∵CE⊥CD,
∴∠ECD=90°,△ECD为等腰直角三角形,
∴∠ACB-∠ECB=∠ECD-∠ECB,
即∠ACE=∠BCD.
∵AC=BC,EC=DC,
∴△ACE≌△BCD(SAS),
∴AE=BD=2,
∴DE=AD-AE=6-2=4.
在等腰Rt△DCE中,CD=DE=2. 6分
(3)①如图2,在DA上截取DE=CD,连接CE,过点C作CF⊥AD于点F,过点O作OH⊥AB于点H,连接AO.
图2
∵△ABC是等边三角形,
∴∠ABC=60°.
∵=,
∴∠ADC=∠ABC=60°.
∵DE=CD,
∴△CDE是等边三角形.
∵☉O的面积为64π,
∴S=πr2=64π,r=8,
∴OA=8.
∵△ABC是等边三角形,OH⊥AB,
∴AB=2AH,∠AOH=60°,∠OAH=30°.
在Rt△AOH中,OH=OA=4,AH=OH=4,
∴AB=2AH=8.
∵△ABC,△EDC为等边三角形,
∴∠ACB=∠ECD=60°,AC=BC,EC=DC,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴S△BCD=S△ACE.
设CD=2y,则EF=DF=y,CF=y.
∵AD=x,
在Rt△ACF中,AC2=AF2+CF2,
∴(8)2=(x-y)2+(y)2,
化简得xy-2y2=x2-96,
∴S=S△ACE+S△ABC=AE·CF+×(8)2
=(x-2y)·y+48
=(xy-2y2)+48
=(x2-96)+48
=x2. 10分
②∵S=x2,
∴要使S最大,则应使x最大,
当AD为☉O的直径时,x最大=16,
∴S最大=×162=64(m2),
即四边形运动区域ABDC面积的最大值为64 m2. 13分
题号 一 二 三 总分 累分人
得分
说明:共有三个大题,26个小题,满分120分,作答时间120分钟.
中考对接点 圆的有关性质(圆周角,圆心角,垂径定理,内切圆,外接圆,圆内接四边形对角互补),点与圆、直线与圆的位置关系,与圆有关的计算(弧长和扇形面积,圆锥的侧、全面积),正多边形与圆,三角形的外心和内心
一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法正确的是 ( )
A.直径不是弦
B.圆既是轴对称图形又是中心对称图形
C.任意三点确定一个圆
D.长度相等的弧是等弧
2.如图,用直角曲尺检查制作成半圆形的工件,则合格的工件是 ( )
3.下列图形中的角,是圆心角的是 ( )
4.如图,AB是☉O的直径,点C,D在☉O上,若∠CDB=35°,则∠CBA的度数为 ( )
A.25°
B.35°
C.45°
D.55°
5.如图,在△ABC中,∠A=80°,点O是△ABC的内心,则∠BOC的度数为 ( )
A.80°
B.100°
C.130°
D.160°
6.唐代李皋发明了“桨轮船”,这种船是原始形态的轮船,是近代明轮航行模式之先导.如图,某桨轮船的轮子被水面截得的弦AB长为4 m,轮子的吃水深度CD为1 m,则该桨轮船的轮子直径为 ( )
A.3 m
B.4 m
C.5 m
D.6 m
7.如图,∠DCE是☉O内接四边形ABCD的一个外角,若∠BOD=140°,则∠DCE的大小为 ( )
A.50°
B.60°
C.70°
D.80°
8.如图,四边形OABC为菱形,点B,C在以点O为圆心的上,若OA=2 cm,∠1=∠2,则的长为 ( )
A. cm
B. cm
C. cm
D. cm
9.若将一个圆心角为120°,半径为6的扇形纸片围成一个圆锥,则该圆锥的底面圆的半径为 ( )
A.1 B.2 C.3 D.4
10.图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB的长分别为半径,圆心角∠O=120°形成的扇面,若OA=3 m,OB=1.5 m,则阴影部分的面积为 ( )
A.4.25π m2 B.3.25π m2 C.3π m2 D.2.25π m2
11.如图,在扇形AOB中,点P在OA上,连接PB,将△OBP沿PB折叠得到△O1BP. 若∠O=70°,且BO1与所在的圆相切于点B,则∠APO1= ( )
A.40° B.50°
C.60° D.70°
12.如图,在6×6的正方形网格中(小正方形的边长为1,小正方形的顶点称为格点),有5个格点M,N,O,P,Q,以点O为圆心,为半径作圆,则在☉O外的点是 ( )
A.P
B.Q
C.M
D.N
13.在一次海事活动中,☉O所在区域是活动区域,其中弦AB与优弧AB所围成的区域是声呐需要探测的区域.现在A处安装一台声呐设备,其探测区域如图1阴影所示,再在B处安装一台同型号声呐设备,A,B两处同时开启声呐设备,恰好能完成所有区域的探测,如图2阴影所示.
如图3,现将声呐设备放置位置改为☉O上D,E,F点,设计三个方案:①在D点放两台该型号的声呐设备
②在D点、E点分别放一台该型号的声呐设备
③在F点放两台该型号的声呐设备
若能完成所有区域的探测,则正确的方案是 ( )
A.①③ B.①②③ C.②③ D.①②
14.如图,在平面直角坐标系xOy中,正六边形OABCDE的边长是2,点E,B分别在x轴,y轴上,则它的内切圆的圆心M的坐标是 ( )
A.(1,)
B.(1,2)
C.(2,)
D.(1,2)
15.如图,在单位长度为1的平面直角坐标系中,曲线是由半径为2,圆心角为120°的多次复制并首尾连接而成的,现有一点P从点A(A为坐标原点)出发,以每秒个单位长度的速度沿曲线向右运动,则在第2024秒点P 的坐标为 ( )
A.(1012,0) B.(2024,0)
C.(1012,0) D.(2024,0)
16.如图,点C在以AB为直径的半圆O上,AB=8,∠CBA=30°,点D在线段AB(不与点A,B重合)上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.有下列结论:
①CE=CF;②∠F=30°;③线段EF的长的最小值为4;④当AD=2时,EF与半圆O相切.
其中正确的个数是 ( )
A.1
B.2
C.3
D.4
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分)
17.如图,这是小华应用直角曲尺来检验半圆形工件是否合格的示意图,其中所应用的数学知识是 .
18.如图,在单位长度为1的正方形网格中建立平面直角坐标系,一条圆弧经过格点A,B,C,则该圆弧所在圆的圆心点D的坐标为 ;若连接AD,CD,∠ADC的度数是 .
19.如图,四边形ABCD内接于☉O,AC为☉O的直径,∠ADB=∠CDB.
(1)∠ACB的度数为 .
(2)若AC=4,∠ACD=30°,则BD的长为 .
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)如图,扇形AOB的圆心角为120°,半径OA为4 cm,求扇形AOB的弧长和面积.
21.(本小题满分9分)如图,这是一个粮仓,底面直径为8 m,粮仓顶部顶点到底面的垂直距离为9 m,粮仓下半部分的高为6 m,观察并回答下列问题.
(1)将下面的图形分别绕虚线旋转一周,能形成粮仓的是 (填字母).
(2)求出该粮仓的容积(计算结果保留π).
22.(本小题满分9分)抖空竹在我国有着悠久的历史,是国家级非物质文化遗产之一.如图1,为弘扬传统文化,某校将抖空竹列入了体育课程.在学习了圆之后,数学兴趣小组的同学们对抖空竹进行了探究,示意图如图2所示.已知绳AC,BD分别与空竹☉O相切于点C,D,且AC=BD,连接左右两个绳柄A,B,AB经过圆心O,交☉O于点E,F.
(1)求证:AE=BF.
(2)若AE=4 cm,AC=8 cm,求两个绳柄之间的距离AB.
图1 图2
23.(本小题满分10分)如图,AB是☉O的直径,BC是☉O的弦,过点C作☉O的切线交BA的延长线于点G,D为切线上一点,DE⊥AB于点E,交BC于点F.
(1)求证:CD=DF.
(2)若C为DG的中点,CD=5,cos D=,求BE的长.
24.(本小题满分10分)已知D为☉O上一点,过点D的切线交弦AB的延长线于点C,连接AD,BD.
(1)如图1,当弦AB为直径时,直接写出∠CDB与∠CAD的数量关系: .
(2)如图2,当AB为非直径时,(1)中的结论还成立吗 若成立,写出证明过程;若不成立,请说明理由.
(3)如图2,BC=4,AB=8,求CD的长.
图1 图2
25.(本小题满分12分)如图,在△OAB中,OA=OB,∠A=30°,☉O与AB相切于点D,交OA于点E,交OB于点F,延长AO交☉O于点C,连接BC.
(1)求证:BC是☉O的切线.
(2)连接OD,DF,CF,判断四边形CODF的形状,并说明理由.
(3)若AE=2,求阴影部分的面积.
26.(本小题满分13分)问题提出
(1)如图1,在等腰Rt△ABC中,∠ACB=90°,D是AB边上一点,以CD为腰作等腰Rt△CDE,且∠DCE=90°,连接BE,则AD与BE的数量关系是 ,位置关系是 .
问题探究
(2)如图2,AB是半圆O的直径,C,D是半圆O上的两点,且AC=BC,BD=2,AD=6,连接CD,求CD的长.
问题解决
(3)图3是某公园的一个面积为64π m2的圆形广场示意图,点O为圆心.公园开发部门计划在该广场内设计一个四边形运动区域ABDC,连接BC,AD,其中等边△ABC为球类运动区域,△BCD为散步区域,设AD的长为x,四边形ABDC的面积为S.
①求S与x之间的函数关系式.
②按照设计要求,为了让人们有更大的运动区域,四边形ABDC的面积越大越好,求四边形运动区域ABDC面积的最大值.
图1 图2 图3
参考答案
1.B 2.D 3.C 4.D 5.C 6.C 7.C 8.C 9.B 10.D 11.B 12.A 13.D 14.A 15.D
16.C 提示:①如图,连接CD,
∵点E与点D关于AC对称,∴CD=CE,∴∠E=∠CDE.
∵DF⊥DE,∴∠EDF=90°,
∴∠E+∠F=90°,∠CDE+∠CDF=90°,
∴∠F=∠CDF,
∴CD=CF,∴CE=CF,故①正确.
②∵点E与点D关于AC对称,
∴DE⊥AC.
∵AB是半圆O的直径,
∴∠ACB=90°,∴BC⊥AC,
∴DE∥BC,
∴DF⊥BC.
若∠F=30°,则∠CDF=30°,
∴∠BCD=60°,
∴∠CDB=90°,
∴只有当CD⊥AB时,∠F=30°,故②不正确.
③∵CD=CE=CF,∴EF=2CD,
要使EF的长最小,则CD的长也要最小.
根据“垂线段最短”,∴CD的长最小时,CD⊥AB.
∵∠ACB=90°,AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4.
∵CD⊥AB,∠CBA=30°,
∴CD=BC=2,
∴EF=2CD=4,
∴EF的长的最小值为4,故③正确.
④当AD=2时,如图,连接OC,
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形,
∴CA=CO.
∵AO=4,AD=2,∴OD=2,
∴AD=OD,
∴∠OCD=∠DCA=30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA=30°,
∴∠OCE=90°,∴OC⊥EF.
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆O相切,故④正确.
故选C.
17.直径所对的圆周角为直角 18.(2,0);90° 19.(1)45° (2)+
20.解:扇形AOB的弧长l==(cm), 4分
扇形AOB的面积S==(cm2). 9分
21.解:(1)D. 4分
(2)粮仓的容积=V圆柱+V圆锥
=π×()2×6+π×()2×(9-6)
=96π+16π
=112π(m3).
答:该粮仓的容积为112π m3. 9分
22.解:(1)证明:如图,连接OC,OD.
∵AC,BD分别与空竹☉O相切于点C,D,
∴∠OCA=∠ODB=90°.
在△OCA和△ODB中,
∴△OCA≌△ODB(SAS),
∴OA=OB.
∵OE=OF,
∴OA-OE=OB-OF,即AE=BF. 4分
(2)设☉O的半径为r cm,
在Rt△AOC中,AC2+OC2=OA2,
∴82+r2=(r+4)2,
解得r=6,
∴OA=6+4=10 cm,
∴AB=2OA=20 cm. 9分
23.解:(1)证明:如图,连接OC.
∵OC=OB,
∴∠OCB=∠B.
∵CD是☉O的切线,
∴∠OCD=90°,
∴∠OCB+∠BCD=90°.
∵DE⊥AB,
∴∠B+∠BFE=90°,
∴∠BCD=∠BFE.
∵∠BFE=∠CFD,
∴∠BCD=∠CFD,
∴CD=DF. 4分
(2)∵C为DG的中点,CD=5,
∴DG=2CD=10,CG=5.
∵DE⊥AB,
∴cos D==,
∴DE=6,EG===8.
∵∠G=∠G,∠OCG=∠DEG=90°,
∴△OCG∽△DEG,
∴==,即==,
∴OG=,OC=,
∴OE=EG-OG=8-=.
∵OB=OC=,
∴BE=OB-OE=-=2. 10分
24.解:(1)∠CDB=∠CAD. 2分
(2)(1)中的结论还成立. 3分
证明:如图,过点B作直径BE,连接DE,OD.
∵CD是☉O的切线,
∴OD⊥CD,
∴∠CDO=90°,
∴∠CDB+∠ODB=90°.
∵BE为☉O的直径,
∴∠EDB=90°,
∴∠ODE+∠ODB=90°,
∴∠CDB=∠ODE.
∵OE=OD,
∴∠E=∠ODE,
∴∠CDB=∠E.
∵=,
∴∠CAD=∠E,
∴∠CDB=∠CAD. 7分
(3)∵∠CDB=∠A,∠DCB=∠ACD,
∴△CBD∽△CDA,
∴=,即=,
∴CD=4. 10分
25.解:(1)证明:如图1,连接OD.
图1
∵OA=OB,∠A=30°,
∴∠AOB=120°,∴∠COB=60°.
∵☉O与AB相切,
∴OD⊥AB,
∴OD平分∠AOB,
∴∠AOD=∠DOB=60°.
在△BOD和△BOC中,
∵OD=OC,∠BOD=∠BOC=60°,OB=OB,
∴△BOD≌△BOC,
∴∠OCB=∠ODB=90°,
∴BC是☉O的切线. 4分
(2)四边形CODF为菱形. 6分
理由:如图2,由(1)知∠COF=∠DOF=60°,OC=OF=OD,
图2
∴△OCF与△ODF都是等边三角形,
∴OC=CF=DF=OD,
∴四边形CODF为菱形. 8分
(3)由(1)知OD⊥AB.
设☉O的半径为r,
∵∠A=30°,OD⊥AB,
∴OA=2OD=2r.
∵AE=2,
∴r+2=2r,
∴r=2.
在Rt△OAD中,AD=OAcos 30°=4×=2,∠AOD=60°,
∴S阴影部分=S△OAD-S扇形DOE=×2×2-=2-. 12分
26.解:(1)相等;垂直. 2分
提示:∵在等腰Rt△ABC中,∠ACB=90°,
∴∠A=∠ABC=45°.
∵∠DCE=∠ACB=90°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE.
∵AC=BC,DC=EC,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CBE=∠A=45°,
∴∠DBE=∠ABC+∠CBE=90°,
∴AD⊥BE.
(2)如图1,过点C作CE⊥CD交AD于点E.
图1
∵AB是半圆O的直径,
∴∠ACB=90°.
∵BC=AC,
∴∠ABC=45°,
∴∠CDA=45°.
∵CE⊥CD,
∴∠ECD=90°,△ECD为等腰直角三角形,
∴∠ACB-∠ECB=∠ECD-∠ECB,
即∠ACE=∠BCD.
∵AC=BC,EC=DC,
∴△ACE≌△BCD(SAS),
∴AE=BD=2,
∴DE=AD-AE=6-2=4.
在等腰Rt△DCE中,CD=DE=2. 6分
(3)①如图2,在DA上截取DE=CD,连接CE,过点C作CF⊥AD于点F,过点O作OH⊥AB于点H,连接AO.
图2
∵△ABC是等边三角形,
∴∠ABC=60°.
∵=,
∴∠ADC=∠ABC=60°.
∵DE=CD,
∴△CDE是等边三角形.
∵☉O的面积为64π,
∴S=πr2=64π,r=8,
∴OA=8.
∵△ABC是等边三角形,OH⊥AB,
∴AB=2AH,∠AOH=60°,∠OAH=30°.
在Rt△AOH中,OH=OA=4,AH=OH=4,
∴AB=2AH=8.
∵△ABC,△EDC为等边三角形,
∴∠ACB=∠ECD=60°,AC=BC,EC=DC,
∴∠ACE=∠BCD,
∴△ACE≌△BCD(SAS),
∴S△BCD=S△ACE.
设CD=2y,则EF=DF=y,CF=y.
∵AD=x,
在Rt△ACF中,AC2=AF2+CF2,
∴(8)2=(x-y)2+(y)2,
化简得xy-2y2=x2-96,
∴S=S△ACE+S△ABC=AE·CF+×(8)2
=(x-2y)·y+48
=(xy-2y2)+48
=(x2-96)+48
=x2. 10分
②∵S=x2,
∴要使S最大,则应使x最大,
当AD为☉O的直径时,x最大=16,
∴S最大=×162=64(m2),
即四边形运动区域ABDC面积的最大值为64 m2. 13分
同课章节目录
