第六章 反比例函数小结与复习课件(33张PPT)2024-2025学年北师大版九年级数学上册
文档属性
| 名称 | 第六章 反比例函数小结与复习课件(33张PPT)2024-2025学年北师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 11:09:47 | ||
图片预览











文档简介
(共33张PPT)
小结与复习
第六章 反比例函数
1. 反比例函数的概念
定义:形如_______ (k 为常数,k ≠ 0) 的函数称为反比例函数,其中 x 是自变量,y 是 x 的反比例函数,k 是比例系数.
三种表达式: 或 xy=k 或 y=kx-1 (k ≠ 0).
防错提醒:(1) k ≠ 0;(2) 自变量 x ≠ 0;(3) 函数值 y ≠ 0.
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k ≠ 0) 的
图象是 ,它是轴对称图形,两条对称轴
为直线 和 .
双曲线
y = x
y = -x
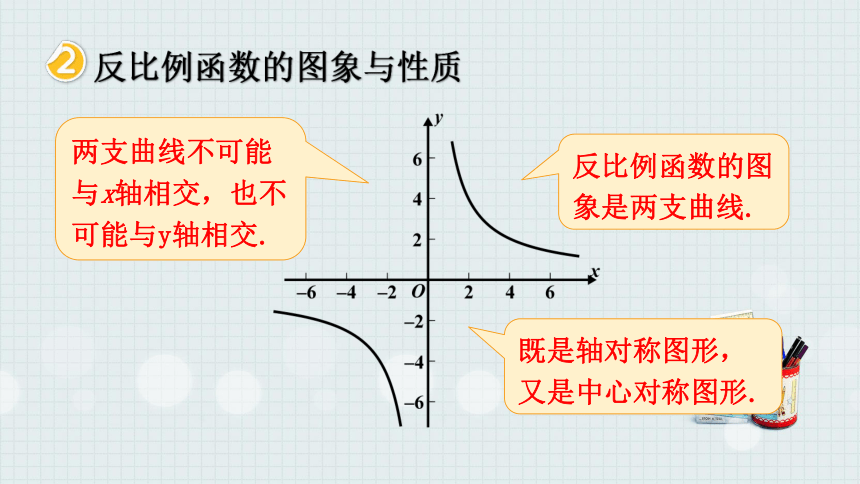
反比例函数的图象与性质
反比例函数的图象是两支曲线.
两支曲线不可能与x轴相交,也不可能与y轴相交.
既是轴对称图形,又是中心对称图形.
反比例函数的图象与性质
当k>0时,图象位于一、三象限,在每一象限内,y的值随x值的增大而减小.
当k<0时,图象位于二、四象限,在每一象限内,y的值随x值的增大而增大。
(2) 反比例函数的性质
图象 所在象限 性质
(k ≠ 0) k>0 一、三象限(x,y 同号) 在每个象限内,y 随 x 的增大而减小
k<0 二、四象限(x,y 异号) 在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
反比例函数的图象与性质
Q
P
S1
S2
反比例函数 (k≠0)中比例系数k的几何意义:
过双曲线y= (k≠0)上任意一点作x轴、y轴的平行线,与坐标轴围成的矩形面积为k的绝对值.
S1=S2=|k|
(3) 反比例函数中比例系数 k 的几何意义
反比例函数图象上的点 (x,y) 具有两坐标之
积 (xy=k) 为常数这一特点,即过反比例函数图象
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 | k |.
推论:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
利用待定系数法确定反比例函数:
①根据两变量之间的反比例关系,设 ;
②代入图象上一个点的坐标,即 x、y 的一对对应
值,求出 k 的值;
③写出表达式.
反比例函数与一次函数的图象的交点的求法
求直线 y=k1x+b (k1 ≠ 0) 和双曲线 (k2 ≠ 0)的交点坐标就是解这两个函数表达式组成的方
程组.
利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确数学问题
注意:实际问题中的两个变量往往都只能取非负值.
考点一 反比例函数的概念
1. 下列函数中哪些是正比例函数?哪些是反比例函数
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
针对练习
2. 已知点 P(1,-3) 在反比例函数 的图象上,则
k 的值是 ( )
A. 3 B. -3 C. D.
B
3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
解析:方法①分别把各点代入反比例函数求出 y1,y2,
y3 的值,再比较出其大小即可;
方法②:根据反比例函数的图象和性质比较.
考点二 反比例函数的图象和性质
例1 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比例函数 的图象上,则 y1,y2,y3 的大小关系是 ( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
D
方法总结:比较反比例函数值的大小,在同一个象限内可根据反比例函数的性质比较,在不同的象限内不能按其性质比较,可根据其正负来确定大小.
4. 已知点 A (x1,y1),B (x2,y2) (x1<0<x2) 都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
y1>y2
针对练习
考点三 与反比例系数 k 有关的问题
例2 如图,两个反比例函数 和 在第一
象限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA
⊥x 轴于点 A,交 C2 于点 B,
则 △POB 的面积为 .
1
5. 如图,在平面直角坐标系中,点 M 为 x 轴正半轴上一点,过点 M 的直线 l∥y 轴,且直线 l 分别与反比例函数 (x>0) 和 (x>0) 的图象交于 P,Q 两点,若 S△POQ = 14,
则 k 的值为 .
-20
针对练习
考点四 反比例函数的应用
例3 如图,已知 A (-4, ),B (-1,2) 是一次函数
y = kx + b 与反比例函数 (m<0) 图象的两个交点,AC⊥x 轴于点 C,BD⊥y 轴于点 D.
(1) 根据图象直接回答:在第二象限内,当 x 取
何值时,一次函数的值大于反比例函数的值;
O
B
A
x
y
C
D
解:当 -4<x<-1 时,一次函数的值大于反比例函数的值.
(2) 求一次函数表达式及 m 的值;
解:把 A(-4, ),B(-1,2) 代入 y = kx + b 中,得
-4k + b = ,
-k + b = 2,
解得
k = ,
b = .
所以一次函数的表达式为 y = x + .
把 B (-1,2) 代入 中,得 m =-1×2=-2.
(3) P 是线段 AB 上的一点,连接 PC,PD,若△PCA 和
△PDB 面积相等,求点 P 的坐标.
解:设点 P 的坐标为 (t, t + ),则 P 点到直线 AC 的距离为 t-(-4),P 点到直线 BD 的距离为 2-( t + ).
∵ △PCA 面积和 △PDB 面积相等,
∴ AC·[t-(-4)] = BD·[2-( t + )],
解得 t = .
∴ 点 P 的坐标为 ( , ).
O
B
A
x
y
C
D
P
方法总结:此类一次函数,反比例函数,二元一次方程组,三角形面积等知识的综合题,关键是理清解题思路. 在平面直角坐标系中,求三角形或四边形面积时,要选取合适的底边和高,正确利用坐标算出线段长度.
6.如图,设反比例函数的表达式为 (k>0).
(1) 若该反比例函数与正比例函数 y = 2x 的图象有一个
交点 P 的纵坐标为 2,求 k 的值;
O
y
x
解:由题意知点 P 在正比例函数 y = 2x 上,把 P 的纵坐标 2 代入该表达式,
得 P (1,2),把 P (1,2) 代入 ,
得到
P
2
针对练习
(2) 若该反比例函数的图象与过点 M (-2,0) 的直线
l:y = kx + b 交于 A,B 两点,如图所示,当 △ABO 的面积为 时,求直线 l 的表达式;
解:把 M (-2,0) 代入 y = kx + b,
得 b = 2k,∴ y = kx + 2k.
O
A
y
B
x
M
l
N
解得 x1 = -3,x2 = 1.
y = kx + 2k,
∴
∴ B (-3,-k),A (1,3k).
∵ △ABO 的面积为
∴ ×2×3k + ×2k =
解得
∴ 直线 l 的表达式为
y = x + .
O
y
x
M
l
N
A (1,3k)
B (-3,-k)
(3) 在第(2)题的条件下,当 x 取何值时,一次函数的
值小于反比例函数的值?
O
y
x
M
l
N
A (1,3k)
B (-3,-k)
解:当 x<-3 或 0<x<1 时,一次函数的值小于反
比例函数的值.
例4 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0≤x≤2 时,y 与 x 的函数表达式;
解:当 0≤x≤2 时,y 与 x 成正比例函数关系.
设 y=kx,由于点 (2,4) 在线段上,所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数表达式;
解:当 x > 2 时,y 与 x 成反比例函数关系,设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有
效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,解得 x≥1,∴ 1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥2,解得 x≤ 4. ∴ 2<x≤4.
所以服药一次,治疗疾病的有效时
间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
7.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x 分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停
止加热,停止加热后,材料温度
逐渐下降,这时温度 y 与时间 x
成反比例函数关系,已知第 12
分钟时,材料温度是14℃.
O
y(℃)
x(min)
12
4
14
28
针对练习
(1) 分别求出该材料加热和停止加热过程中 y 与 x 的函
数关系式(写出 x 的取值范围);
O
y(℃)
x(min)
12
4
14
28
答案:
y =
4x + 4 (0 ≤ x ≤ 6),
(x>6).
(2) 根据该食品制作要求,在材料温度不低于 12℃ 的
这段时间内,需要对该材料进行特殊处理,那么
对该材料进行特殊处理的时间为多少分钟
解:当y = 12时,y = 4x+4,解得 x = 2.
由 ,解得x = 14.
所以对该材料进行特殊
处理所用的时间为
14-2 = 12 (分钟).
O
y(℃)
x(min)
12
4
14
28
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
见教材章末练习
小结与复习
第六章 反比例函数
1. 反比例函数的概念
定义:形如_______ (k 为常数,k ≠ 0) 的函数称为反比例函数,其中 x 是自变量,y 是 x 的反比例函数,k 是比例系数.
三种表达式: 或 xy=k 或 y=kx-1 (k ≠ 0).
防错提醒:(1) k ≠ 0;(2) 自变量 x ≠ 0;(3) 函数值 y ≠ 0.
2. 反比例函数的图象和性质
(1) 反比例函数的图象:反比例函数 (k ≠ 0) 的
图象是 ,它是轴对称图形,两条对称轴
为直线 和 .
双曲线
y = x
y = -x
反比例函数的图象与性质
反比例函数的图象是两支曲线.
两支曲线不可能与x轴相交,也不可能与y轴相交.
既是轴对称图形,又是中心对称图形.
反比例函数的图象与性质
当k>0时,图象位于一、三象限,在每一象限内,y的值随x值的增大而减小.
当k<0时,图象位于二、四象限,在每一象限内,y的值随x值的增大而增大。
(2) 反比例函数的性质
图象 所在象限 性质
(k ≠ 0) k>0 一、三象限(x,y 同号) 在每个象限内,y 随 x 的增大而减小
k<0 二、四象限(x,y 异号) 在每个象限内,y 随 x 的增大而增大
x
y
o
x
y
o
反比例函数的图象与性质
Q
P
S1
S2
反比例函数 (k≠0)中比例系数k的几何意义:
过双曲线y= (k≠0)上任意一点作x轴、y轴的平行线,与坐标轴围成的矩形面积为k的绝对值.
S1=S2=|k|
(3) 反比例函数中比例系数 k 的几何意义
反比例函数图象上的点 (x,y) 具有两坐标之
积 (xy=k) 为常数这一特点,即过反比例函数图象
上任意一点,向两坐标轴作垂线,两条垂线与坐
标轴所围成的矩形的面积为常数 | k |.
推论:过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积
为常数 .
3. 反比例函数的应用
利用待定系数法确定反比例函数:
①根据两变量之间的反比例关系,设 ;
②代入图象上一个点的坐标,即 x、y 的一对对应
值,求出 k 的值;
③写出表达式.
反比例函数与一次函数的图象的交点的求法
求直线 y=k1x+b (k1 ≠ 0) 和双曲线 (k2 ≠ 0)的交点坐标就是解这两个函数表达式组成的方
程组.
利用反比例函数相关知识解决实际问题
过程:分析实际情境→建立函数模型→明确数学问题
注意:实际问题中的两个变量往往都只能取非负值.
考点一 反比例函数的概念
1. 下列函数中哪些是正比例函数?哪些是反比例函数
① y = 3x-1
② y = 2x2
⑤ y = 3x
③
④
⑥
⑦
⑧
针对练习
2. 已知点 P(1,-3) 在反比例函数 的图象上,则
k 的值是 ( )
A. 3 B. -3 C. D.
B
3. 若 是反比例函数,则 a 的值为 ( )
A. 1 B. -1 C. ±1 D. 任意实数
A
解析:方法①分别把各点代入反比例函数求出 y1,y2,
y3 的值,再比较出其大小即可;
方法②:根据反比例函数的图象和性质比较.
考点二 反比例函数的图象和性质
例1 已知点 A(1,y1),B(2,y2),C(-3,y3) 都在反比例函数 的图象上,则 y1,y2,y3 的大小关系是 ( )
A. y3<y1<y2 B. y1<y2<y3
C. y2<y1<y3 D. y3<y2<y1
D
方法总结:比较反比例函数值的大小,在同一个象限内可根据反比例函数的性质比较,在不同的象限内不能按其性质比较,可根据其正负来确定大小.
4. 已知点 A (x1,y1),B (x2,y2) (x1<0<x2) 都在反比例函数 (k<0) 的图象上,则 y1 与 y2 的大小关系 (从大到小) 为 .
y1>y2
针对练习
考点三 与反比例系数 k 有关的问题
例2 如图,两个反比例函数 和 在第一
象限内的图象分别是 C1 和 C2,设点 P 在 C1 上,PA
⊥x 轴于点 A,交 C2 于点 B,
则 △POB 的面积为 .
1
5. 如图,在平面直角坐标系中,点 M 为 x 轴正半轴上一点,过点 M 的直线 l∥y 轴,且直线 l 分别与反比例函数 (x>0) 和 (x>0) 的图象交于 P,Q 两点,若 S△POQ = 14,
则 k 的值为 .
-20
针对练习
考点四 反比例函数的应用
例3 如图,已知 A (-4, ),B (-1,2) 是一次函数
y = kx + b 与反比例函数 (m<0) 图象的两个交点,AC⊥x 轴于点 C,BD⊥y 轴于点 D.
(1) 根据图象直接回答:在第二象限内,当 x 取
何值时,一次函数的值大于反比例函数的值;
O
B
A
x
y
C
D
解:当 -4<x<-1 时,一次函数的值大于反比例函数的值.
(2) 求一次函数表达式及 m 的值;
解:把 A(-4, ),B(-1,2) 代入 y = kx + b 中,得
-4k + b = ,
-k + b = 2,
解得
k = ,
b = .
所以一次函数的表达式为 y = x + .
把 B (-1,2) 代入 中,得 m =-1×2=-2.
(3) P 是线段 AB 上的一点,连接 PC,PD,若△PCA 和
△PDB 面积相等,求点 P 的坐标.
解:设点 P 的坐标为 (t, t + ),则 P 点到直线 AC 的距离为 t-(-4),P 点到直线 BD 的距离为 2-( t + ).
∵ △PCA 面积和 △PDB 面积相等,
∴ AC·[t-(-4)] = BD·[2-( t + )],
解得 t = .
∴ 点 P 的坐标为 ( , ).
O
B
A
x
y
C
D
P
方法总结:此类一次函数,反比例函数,二元一次方程组,三角形面积等知识的综合题,关键是理清解题思路. 在平面直角坐标系中,求三角形或四边形面积时,要选取合适的底边和高,正确利用坐标算出线段长度.
6.如图,设反比例函数的表达式为 (k>0).
(1) 若该反比例函数与正比例函数 y = 2x 的图象有一个
交点 P 的纵坐标为 2,求 k 的值;
O
y
x
解:由题意知点 P 在正比例函数 y = 2x 上,把 P 的纵坐标 2 代入该表达式,
得 P (1,2),把 P (1,2) 代入 ,
得到
P
2
针对练习
(2) 若该反比例函数的图象与过点 M (-2,0) 的直线
l:y = kx + b 交于 A,B 两点,如图所示,当 △ABO 的面积为 时,求直线 l 的表达式;
解:把 M (-2,0) 代入 y = kx + b,
得 b = 2k,∴ y = kx + 2k.
O
A
y
B
x
M
l
N
解得 x1 = -3,x2 = 1.
y = kx + 2k,
∴
∴ B (-3,-k),A (1,3k).
∵ △ABO 的面积为
∴ ×2×3k + ×2k =
解得
∴ 直线 l 的表达式为
y = x + .
O
y
x
M
l
N
A (1,3k)
B (-3,-k)
(3) 在第(2)题的条件下,当 x 取何值时,一次函数的
值小于反比例函数的值?
O
y
x
M
l
N
A (1,3k)
B (-3,-k)
解:当 x<-3 或 0<x<1 时,一次函数的值小于反
比例函数的值.
例4 病人按规定的剂量服用某种药物,测得服药后 2 小时,每毫升血液中的含药量达到最大值为 4 毫克. 已知服药后,2 小时前每毫升血液中的含药量 y (单位:毫克)与时间 x (单位:小时) 成正比例;2 小时后 y 与 x 成反比例 (如图). 根据以上信息解答下列问题:
(1) 求当 0≤x≤2 时,y 与 x 的函数表达式;
解:当 0≤x≤2 时,y 与 x 成正比例函数关系.
设 y=kx,由于点 (2,4) 在线段上,所以 4=2k,k=2,即 y=2x.
O
y/毫克
x/小时
2
4
(2) 求当 x > 2 时,y 与 x 的函数表达式;
解:当 x > 2 时,y 与 x 成反比例函数关系,设
解得 k =8.
由于点 (2,4) 在反比例函数的图象上,
所以
即
O
y/毫克
x/小时
2
4
(3) 若每毫升血液中的含药量不低于 2 毫克时治疗有
效,则服药一次,治疗疾病的有效时间是多长?
解:当 0≤x≤2 时,含药量不低于 2 毫克,即 2x≥2,解得 x≥1,∴ 1≤x≤2;
当 x>2 时,含药量不低于 2 毫克,
即 ≥2,解得 x≤ 4. ∴ 2<x≤4.
所以服药一次,治疗疾病的有效时
间是 1+2=3 (小时).
O
y/毫克
x/小时
2
4
7.如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x 分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停
止加热,停止加热后,材料温度
逐渐下降,这时温度 y 与时间 x
成反比例函数关系,已知第 12
分钟时,材料温度是14℃.
O
y(℃)
x(min)
12
4
14
28
针对练习
(1) 分别求出该材料加热和停止加热过程中 y 与 x 的函
数关系式(写出 x 的取值范围);
O
y(℃)
x(min)
12
4
14
28
答案:
y =
4x + 4 (0 ≤ x ≤ 6),
(x>6).
(2) 根据该食品制作要求,在材料温度不低于 12℃ 的
这段时间内,需要对该材料进行特殊处理,那么
对该材料进行特殊处理的时间为多少分钟
解:当y = 12时,y = 4x+4,解得 x = 2.
由 ,解得x = 14.
所以对该材料进行特殊
处理所用的时间为
14-2 = 12 (分钟).
O
y(℃)
x(min)
12
4
14
28
反比例函数
定义
图象
性质
x,y 的取值范围
增减性
对称性
k 的几何意义
应用
在实际生活中的应用
在物理学科中的应用
见教材章末练习
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
