专题二 综合与实践 课件(共27张PPT) 2025年中考数学人教版一轮复习考点探究(广西)
文档属性
| 名称 | 专题二 综合与实践 课件(共27张PPT) 2025年中考数学人教版一轮复习考点探究(广西) |

|
|
| 格式 | pptx | ||
| 文件大小 | 467.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 18:56:40 | ||
图片预览







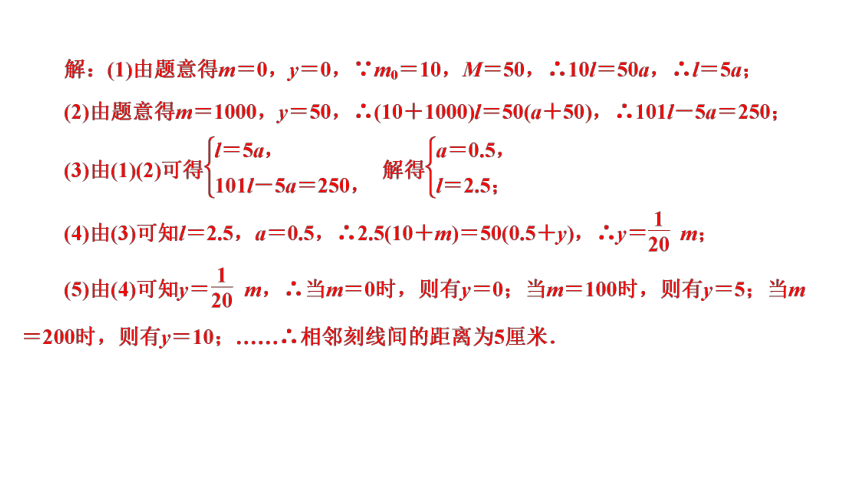
文档简介
(共27张PPT)
数 学
专题二 综合与实践(2024.23,2023.25,北部湾5年1考)
1.(2024广西)【综合与实践】在综合与实践课上,数学兴趣小组通过洗一套夏季校服,探索清洗衣物的节约用水策略.
【洗衣过程】
步骤一:将校服放进清水中,加入洗衣液,充分浸泡揉搓后拧干;
步骤二:将拧干后的校服放进清水中,充分漂洗后拧干.重复操作步骤二,直至校服上残留洗衣液浓度达到洗衣目标.
假设第一次漂洗前校服上残留洗衣液浓度为0.2%,每次拧干后校服上都残留0.5 kg水.
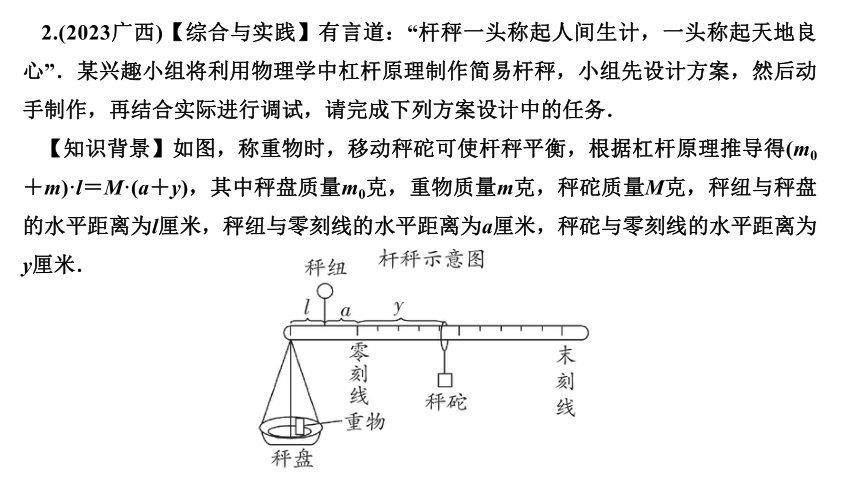
2.(2023广西)【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤,小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得(m0+m)·l=M·(a+y),其中秤盘质量m0克,重物质量m克,秤砣质量M克,秤纽与秤盘的水平距离为l厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
【方案设计】目标:设计简易杆秤.设定m0=10,M=50,最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
任务一:确定l和a的值.
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;
(2)当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于l,a的方程;
(3)根据(1)和(2)所列方程,求出l和a的值;
任务二:确定刻线的位置.
(4)根据任务一,求y关于m的函数解析式;
(5)从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离.
3.(2024柳州三模)综合与实践
【知识背景】大豆,通称黄豆,属一年生草本,是我国重要粮食作物之一,已有五千年栽培历史,古称“菽”.某校综合实践小组以探究“大豆种植密度优化方案”为主题开展实验研究,探究大豆产量与种植密度的关系.
【研究步骤】
(1)在劳动实践基地中选定6块单位面积(1平方米)的地块作为试验田,并选定适宜的大豆品种;
(2)在不同试验田中种植株数不同的大豆,严格控制影响大豆生长的其他变量,在大豆成熟期,对每株大豆的产量进行统计;
(3)数据分析,形成结论.
【试验数据】
试验田编号 1 2 3 4 5 6
单位面积试验田种植株数x(株) 30 40 50 60 70 80
单株的平均产量y(粒) 51 46 41 36 31 26
【数学建模】请根据以上材料完成下列任务:
(1)根据表中信息推理,单位面积试验田中大豆单株的平均产量y(粒)是种植株数x(株)的______函数(选填“一次”“二次”“反比例”),y与x的函数关系式为____________
(30≤x≤80);
(2)若要使单位面积试验田中大豆的总产量(单位:粒)最大,请通过计算说明单位面积试验田中大豆植株种植数量的方案;
(3)单位面积试验田中大豆的总产量能否达到2160粒,请说明理由.
一次
4.(2024南宁模拟)综合与实践
【问题提出】某班开展课外锻炼,有7位同学组队参加跳长绳运动,如何才能顺利开展活动呢?
【实践活动】在体育老师的指导下,队员们进行了以下实践:
步骤一:收集身高数据如下
队员 甲 乙 丙 丁 戊 己 庚
身高/m 1.70 1.70 1.73 1.60 1.68 1.80 1.60
步骤二:为增加甩绳的稳定度,确定两位身高较高且相近的甲、乙队员甩绳,其余队员跳绳;
步骤三:所有队员站成一排,跳绳队员按照中间高、两端低的方式排列,同时7名队员每两人间的距离至少为0.5 m才能保证安全;
步骤四:如图①,两位甩绳队员通过多次实践发现,当两人的水平距离AC=4 m,手离地面的高度AB=CD=1.2 m,绳子最高点距离地面2 m时,效果最佳;
【问题解决】如图②,当绳子甩动到最高点时的形状近似看成一条抛物线,若以AC所在直线为x轴,AB所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式;
(2)最高的队员位于AC中点,其余跳绳队员对称安排在其两侧.
①当跳绳队员之间正好保持0.5 m的距离时,长绳能否高过所有跳绳队员的头顶?
②在保证安全的情况下,求最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围.
解:(1)当l为20时,BC=20-2a,∴a(20-2a)=32,即a2-10a+16=0,解得a1=2,a2=8,
当a=2时,20-2a=16>12,不符合题意舍去.
当a=8时,20-2a=4<12,符合题意,∴a=8;
(2)①S=a(20-2a)(4≤a<10);
②S=a(20-2a)=-2a2+20a=-2(a-5)2+50,
∵-2<0,∴当a=5时,S有最大值,最大值为50;
6.综合与实践
【问题背景】鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰,国旗上的每颗星都是标准五角星,为了增强学生的国家荣誉感、民族自豪感等,数学王老师组织学生对五角星进行了较深入的研究,其中智慧数学小组发现国旗上五角星的五个角都是顶角为36°的等腰三角形,对此三角形产生了极大的兴趣并展开探究.
【探究发现】如图①,在△ABC中,∠A=36°,AB=AC.
(1)操作发现:将△ABC折叠,使边BC落在边BA上,点C的对应点是点E,折痕交AC于点D,连接DE,DB,则∠BDC=____°,设AC=2,BC=x,那么DC=________(用含x的式子表示);
72
2-x
数 学
专题二 综合与实践(2024.23,2023.25,北部湾5年1考)
1.(2024广西)【综合与实践】在综合与实践课上,数学兴趣小组通过洗一套夏季校服,探索清洗衣物的节约用水策略.
【洗衣过程】
步骤一:将校服放进清水中,加入洗衣液,充分浸泡揉搓后拧干;
步骤二:将拧干后的校服放进清水中,充分漂洗后拧干.重复操作步骤二,直至校服上残留洗衣液浓度达到洗衣目标.
假设第一次漂洗前校服上残留洗衣液浓度为0.2%,每次拧干后校服上都残留0.5 kg水.
2.(2023广西)【综合与实践】有言道:“杆秤一头称起人间生计,一头称起天地良心”.某兴趣小组将利用物理学中杠杆原理制作简易杆秤,小组先设计方案,然后动手制作,再结合实际进行调试,请完成下列方案设计中的任务.
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理推导得(m0+m)·l=M·(a+y),其中秤盘质量m0克,重物质量m克,秤砣质量M克,秤纽与秤盘的水平距离为l厘米,秤纽与零刻线的水平距离为a厘米,秤砣与零刻线的水平距离为y厘米.
【方案设计】目标:设计简易杆秤.设定m0=10,M=50,最大可称重物质量为1000克,零刻线与末刻线的距离定为50厘米.
任务一:确定l和a的值.
(1)当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于l,a的方程;
(2)当秤盘放入质量为1000克的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于l,a的方程;
(3)根据(1)和(2)所列方程,求出l和a的值;
任务二:确定刻线的位置.
(4)根据任务一,求y关于m的函数解析式;
(5)从零刻线开始,每隔100克在秤杆上找到对应刻线,请写出相邻刻线间的距离.
3.(2024柳州三模)综合与实践
【知识背景】大豆,通称黄豆,属一年生草本,是我国重要粮食作物之一,已有五千年栽培历史,古称“菽”.某校综合实践小组以探究“大豆种植密度优化方案”为主题开展实验研究,探究大豆产量与种植密度的关系.
【研究步骤】
(1)在劳动实践基地中选定6块单位面积(1平方米)的地块作为试验田,并选定适宜的大豆品种;
(2)在不同试验田中种植株数不同的大豆,严格控制影响大豆生长的其他变量,在大豆成熟期,对每株大豆的产量进行统计;
(3)数据分析,形成结论.
【试验数据】
试验田编号 1 2 3 4 5 6
单位面积试验田种植株数x(株) 30 40 50 60 70 80
单株的平均产量y(粒) 51 46 41 36 31 26
【数学建模】请根据以上材料完成下列任务:
(1)根据表中信息推理,单位面积试验田中大豆单株的平均产量y(粒)是种植株数x(株)的______函数(选填“一次”“二次”“反比例”),y与x的函数关系式为____________
(30≤x≤80);
(2)若要使单位面积试验田中大豆的总产量(单位:粒)最大,请通过计算说明单位面积试验田中大豆植株种植数量的方案;
(3)单位面积试验田中大豆的总产量能否达到2160粒,请说明理由.
一次
4.(2024南宁模拟)综合与实践
【问题提出】某班开展课外锻炼,有7位同学组队参加跳长绳运动,如何才能顺利开展活动呢?
【实践活动】在体育老师的指导下,队员们进行了以下实践:
步骤一:收集身高数据如下
队员 甲 乙 丙 丁 戊 己 庚
身高/m 1.70 1.70 1.73 1.60 1.68 1.80 1.60
步骤二:为增加甩绳的稳定度,确定两位身高较高且相近的甲、乙队员甩绳,其余队员跳绳;
步骤三:所有队员站成一排,跳绳队员按照中间高、两端低的方式排列,同时7名队员每两人间的距离至少为0.5 m才能保证安全;
步骤四:如图①,两位甩绳队员通过多次实践发现,当两人的水平距离AC=4 m,手离地面的高度AB=CD=1.2 m,绳子最高点距离地面2 m时,效果最佳;
【问题解决】如图②,当绳子甩动到最高点时的形状近似看成一条抛物线,若以AC所在直线为x轴,AB所在的直线为y轴,建立平面直角坐标系.
(1)求抛物线的解析式;
(2)最高的队员位于AC中点,其余跳绳队员对称安排在其两侧.
①当跳绳队员之间正好保持0.5 m的距离时,长绳能否高过所有跳绳队员的头顶?
②在保证安全的情况下,求最左边的跳绳队员与离他最近的甩绳队员之间距离的取值范围.
解:(1)当l为20时,BC=20-2a,∴a(20-2a)=32,即a2-10a+16=0,解得a1=2,a2=8,
当a=2时,20-2a=16>12,不符合题意舍去.
当a=8时,20-2a=4<12,符合题意,∴a=8;
(2)①S=a(20-2a)(4≤a<10);
②S=a(20-2a)=-2a2+20a=-2(a-5)2+50,
∵-2<0,∴当a=5时,S有最大值,最大值为50;
6.综合与实践
【问题背景】鲜艳的中华人民共和国国旗始终是当代中华儿女永不褪色的信仰,国旗上的每颗星都是标准五角星,为了增强学生的国家荣誉感、民族自豪感等,数学王老师组织学生对五角星进行了较深入的研究,其中智慧数学小组发现国旗上五角星的五个角都是顶角为36°的等腰三角形,对此三角形产生了极大的兴趣并展开探究.
【探究发现】如图①,在△ABC中,∠A=36°,AB=AC.
(1)操作发现:将△ABC折叠,使边BC落在边BA上,点C的对应点是点E,折痕交AC于点D,连接DE,DB,则∠BDC=____°,设AC=2,BC=x,那么DC=________(用含x的式子表示);
72
2-x
同课章节目录
