专题六 几何探究题 课件(共50张PPT) 2025年中考数学人教版一轮复习考点探究(广西)
文档属性
| 名称 | 专题六 几何探究题 课件(共50张PPT) 2025年中考数学人教版一轮复习考点探究(广西) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 18:58:34 | ||
图片预览











文档简介
(共50张PPT)
数 学
专题六 几何探究题
类型一 与旋转有关
(2024.26)
例1 (2024广西)如图①,在△ABC中,∠B=90°,AB=6,AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
证明:∵MO垂直平分AC,∴OA=OC,
∴∠A=∠ACO,∵CO平分∠ACB,
∴∠ACO=∠OCB,∴∠A=∠OCB,
∵∠B=∠B,∴△ABC∽△CBO;
(2)如图②,将△AOC绕点O逆时针旋转得到△A′OC′,旋转角为α(0°<α<360°),连接A′M,C′M.
①求△A′MC′面积的最大值及此时旋转角α的度数,并说明 理由;
②当△A′MC′是直角三角形时,请直接写出旋转角α的度数.
【思路引导】从问题出发,要证△ABC∽△CBO,已知两个三角形有一个公共角,则只需证一角相等即可;
【思路引导】△A′MC′的底A′C′是定长,所以只要找到边A′C′上的高的最大值就可求出△A′MC′面积的最大值;
【思路引导】只有可能是∠A′MC′=90°,由特殊三角形和旋转的性质猜测当点C′与A重合时和当A′与C重合时满足∠A′MC′=90°,进而求旋转角即可.
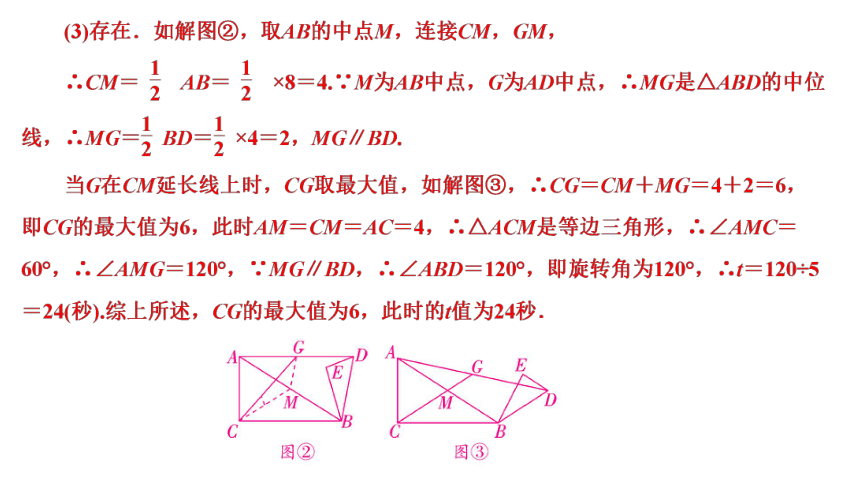
1.(2024南宁一模)【情境呈现】在一次数学兴趣小组活动中,小明同学将一大一小两个三角板按照如图①所示的方式摆放,其中∠ACB=∠DEB=90°,∠ABC=∠DBE=30°,BD=AC=4.他把三角板ABC固定好后,将三角板DEB从图①所示的位置开始绕点B按顺时针方向旋转,每秒转动5°,设转动时间为t秒(0<t≤30).
【问题应用】
(1)请直接写出图①中线段AD的值;
(2)如图②,在三角板DEB旋转的过程中,连接AD,当四边形ACBD是矩形时,求t的值;
【问题探究】
(3)如图③,在三角板DEB旋转的过程中,取AD的中点G,连接CG,CG是否存在最大值?若存在,请求出CG的最大值,并直接写出此时的t值;若不存在,请说明理由.
解:(1)线段AD的值为4;
(2)当四边形ACBD是矩形时,如解图①,此时∠CBD=90°.
∵∠ABC=30°,∴∠ABD=∠CBD-∠ABC=60°,即旋转角为60°,∴t=60÷5=12(秒),∴t的值为12秒;
解:(1)①b=-4a;
②∵函数图象经过点(1,3),∴a+b+c=3,∵b=-4a,∴c=3a+3,∴抛物线的解析式为y=ax2-4ax+3a+3.
∵点(x1,y1),(x1+2,y2)在抛物线y=ax2-4ax+3a+3(a>0)上,∴y1=ax12-4ax1+3a+3,y2=a(x1+2)2-4a(x1+2)+3a+3,
∴y1+y2=2ax12-4ax1+2a+6=2a(x1-1)2+6,
∵a>0,∴y1+y2的最小值为6;
2.(2024山西)【问题情境】如图①,四边形ABCD是菱形,过点A作AE⊥BC于点E,过点C作CF⊥AD于点F.
【猜想证明】
(1)判断四边形AECF的形状,并说明理由;
【深入探究】
(2)将图①中的△ABE绕点A逆时针旋转,得到△AHG,点E,B的对应点分别为点G,H.
①当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.如图②,猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若AB=5,BE=4,直接写出四边形AMNQ的面积.
解:(1)四边形AECF为矩形.
理由如下:∵AE⊥BC,CF⊥AD,∴∠AEC=90°,∠AFC=90°,
∵四边形ABCD为菱形,∴AD∥BC,∴∠AFC+∠ECF=180°,∴∠ECF=180°-∠AFC=90°,∴四边形AECF为矩形;
(2)①CH=MD.理由如下:∵四边形ABCD为菱形,∴AB=AD,∠B=∠D.∵△ABE旋转得到△AHG,∴AB=AH,∠B=∠H,∴AH=AD,∠H=∠D.
∵∠HAM=∠DAC,∴△HAM≌△DAC(ASA),∴AM=AC,
∴AH-AC=AD-AM,∴CH=MD;
类型二 与折叠有关
(2023.26)
例2 (2022北部湾)【探究与证明】折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.
【动手操作】如图①,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为B′,E′,展平纸片,连接AB′,BB′,BE′.请完成:
(1)观察图①中∠1,∠2和∠3,试猜想这三个角的大小关系;
解:(1)∠1=∠2=∠3;
(2)证明(1)中的猜想;
证明:设AM,EF交于点O,
由题意得EF是AB的垂直平分线,AM是BB′的垂直平分线,AB=AB′,∴AB′=BB′,OA=OB=OB′,∴AB′=BB′=AB,O为△ABB′的外心,∴∠ABB′=60°,∴∠1=∠2=30°.
∵四边形ABCD是矩形,∴∠ABC=90°,∴∠3=90°-60°=30°,∴∠1=∠2=∠3;
【类比操作】如图②,N为矩形纸片ABCD的边AD上的一点,连接BN,在AB上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕EF;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为B′,P′,展平纸片,连接BB′,P′B′.请完成:
(3)求证:BB′是∠NBC的一条三等分线.
证明:如图,设l与EF交于点O,连接OP′,OP,OB,PB′,同理(2)得OB=OB′=OP=OP′,BP′=PB′=BB′,∴∠P′BO=∠B′BO,∠OBB′=∠BB′O,
∵EF∥BC,∴∠OB′B=∠B′BC,∴∠P′BO=∠B′BO=∠B′BC,∴BB′是∠NBC的一条三等分线.
【思路引导】设AM,EF交于点O,可推出点O是等边三角形ABB′的外心,从而得出∠1和∠2的度数,进一步得出结论;
【思路引导】设l与EF交于点O,连接OP′,OP,OB,PB′.同理(2)可得OB=OB′=OP=OP′,BP′=PB′=BB′,从而得几组相等的角,根据EF∥BC得出一组等角,等量代换即可得证.
3.(2024钦州一模)【问题情境】如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,该怎么办呢?
【实践探究】小西进行了以下操作研究(如图①):
第1步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平.
第2步:再次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到了线段BN.
小雅在小西研究的基础上,再次动手操作(如图②).
(1)直接写出BE和BN的数量关系:________________;
(2)请求出∠ABM的度数;
(3)求证:四边形BGHM是菱形.
(3)证明:由(1)(2)知∠NBM=∠ABM=30°,
∵四边形ABCD是矩形,∴AD∥BC,∠A=∠ABC=90°,∴∠CBN=30°,∴∠MBN=∠CBN=30°.由翻折可知∠BNM=∠A=90°,∴∠BNM=∠BNG=90°,∵BN=BN,
∴△BNM≌△BNG(ASA),∴BM=BG,
∵AD∥BC,∴∠BHM=∠CBN=30°,∴∠BHM=∠MBN=30°,
∴BM=HM,∴BG=HM,∵AD∥BC,
∴四边形BGHM是平行四边形,
∵BM=HM,∴四边形BGHM是菱形.
(1)证明:∵四边形ABCD是正方形,∴AB=DA,∠ABE=90°=∠DAQ,∴∠QAO+∠OAD=90°,
∵AE⊥DQ,∴∠ADO+∠OAD=90°,∴∠QAO=∠ADO,
∴△ABE≌△DAQ(ASA),∴AE=DQ.
∵DQ⊥AE,GF⊥AE,∴DQ∥GF,∵FQ∥DG,∴四边形DQFG是平行四边形,∴GF=DQ,∵AE=DQ,∴AE=FG;
类型三 与动点有关
(北部湾5年2考)
例3 (2022北部湾)已知∠MON=α,点A,B分别在射线OM,ON上运动,AB=6.
(1)如图①,若α=90°,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为A′,B′,D′,连接OD,OD′.判断OD与OD′有什么样的数量关系?证明你的结论;
(2)如图②,若α=60°,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离;
(3)如图③,若α=45°,当点A,B运动到什么位置时,△AOB的面积最大?请说明理由,并求出△AOB面积的最大值.
【思路引导】根据“直角三角形斜边中线等于斜边一半”分别求出OD,OD′的长,进而得出结论;
【思路引导】作△AOB的外接圆⊙I,观察图形,找出点O与点C距离最大时,点O′的位置,结合已知条件进而求得结果;
【思路引导】作等腰直角三角形AIB,以点I为圆心,AI长为半径作⊙I,取AB的中点C,连接CI并延长交⊙I于点O,此时△AOB的面积最大,进一步求得结果.
5.(2024广西模拟)【探究与证明】学校开展艺术作品展示活动,九年级数学兴趣小组制作菱形木质框架时(如图①),通过平移支架开展数学探究,探索数学奥秘.
【动手操作】菱形框架固定不动,在AC上平移支架∠EGF的顶点G.
如图①,在菱形ABCD中,已知∠B=∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.
如图②,当顶点G运动到与点A重合时,观察图中EC,CF和BC,试猜想这三条线段之间的数量关系,并证明你的猜想;
6.(2024贵州)如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
【操作判断】
(1)如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为______度;
【问题探究】
(2)如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(1)解:如图①,PC即为所求;90;
(2)证明:如图②,过P作PC⊥OB于点C.
由(1)知四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,∴PA=PC,∴矩形OAPC是正方形,∴OA=AP=PC=OC,∠APC=90°,
∵PN⊥PM,∴∠APM=∠CPN=90°-∠MPC,
又∠MAP=∠NCP=90°,AP=CP,∴△APM≌△CPN(ASA),
∴AM=CN,∴OM+ON=OM+OC+CN=OM+AM+OC=OA+OC=2AP,∴OM+ON=2PA;
【拓展应用】
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图③.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
数 学
专题六 几何探究题
类型一 与旋转有关
(2024.26)
例1 (2024广西)如图①,在△ABC中,∠B=90°,AB=6,AC的垂直平分线分别交AC,AB于点M,O,CO平分∠ACB.
(1)求证:△ABC∽△CBO;
证明:∵MO垂直平分AC,∴OA=OC,
∴∠A=∠ACO,∵CO平分∠ACB,
∴∠ACO=∠OCB,∴∠A=∠OCB,
∵∠B=∠B,∴△ABC∽△CBO;
(2)如图②,将△AOC绕点O逆时针旋转得到△A′OC′,旋转角为α(0°<α<360°),连接A′M,C′M.
①求△A′MC′面积的最大值及此时旋转角α的度数,并说明 理由;
②当△A′MC′是直角三角形时,请直接写出旋转角α的度数.
【思路引导】从问题出发,要证△ABC∽△CBO,已知两个三角形有一个公共角,则只需证一角相等即可;
【思路引导】△A′MC′的底A′C′是定长,所以只要找到边A′C′上的高的最大值就可求出△A′MC′面积的最大值;
【思路引导】只有可能是∠A′MC′=90°,由特殊三角形和旋转的性质猜测当点C′与A重合时和当A′与C重合时满足∠A′MC′=90°,进而求旋转角即可.
1.(2024南宁一模)【情境呈现】在一次数学兴趣小组活动中,小明同学将一大一小两个三角板按照如图①所示的方式摆放,其中∠ACB=∠DEB=90°,∠ABC=∠DBE=30°,BD=AC=4.他把三角板ABC固定好后,将三角板DEB从图①所示的位置开始绕点B按顺时针方向旋转,每秒转动5°,设转动时间为t秒(0<t≤30).
【问题应用】
(1)请直接写出图①中线段AD的值;
(2)如图②,在三角板DEB旋转的过程中,连接AD,当四边形ACBD是矩形时,求t的值;
【问题探究】
(3)如图③,在三角板DEB旋转的过程中,取AD的中点G,连接CG,CG是否存在最大值?若存在,请求出CG的最大值,并直接写出此时的t值;若不存在,请说明理由.
解:(1)线段AD的值为4;
(2)当四边形ACBD是矩形时,如解图①,此时∠CBD=90°.
∵∠ABC=30°,∴∠ABD=∠CBD-∠ABC=60°,即旋转角为60°,∴t=60÷5=12(秒),∴t的值为12秒;
解:(1)①b=-4a;
②∵函数图象经过点(1,3),∴a+b+c=3,∵b=-4a,∴c=3a+3,∴抛物线的解析式为y=ax2-4ax+3a+3.
∵点(x1,y1),(x1+2,y2)在抛物线y=ax2-4ax+3a+3(a>0)上,∴y1=ax12-4ax1+3a+3,y2=a(x1+2)2-4a(x1+2)+3a+3,
∴y1+y2=2ax12-4ax1+2a+6=2a(x1-1)2+6,
∵a>0,∴y1+y2的最小值为6;
2.(2024山西)【问题情境】如图①,四边形ABCD是菱形,过点A作AE⊥BC于点E,过点C作CF⊥AD于点F.
【猜想证明】
(1)判断四边形AECF的形状,并说明理由;
【深入探究】
(2)将图①中的△ABE绕点A逆时针旋转,得到△AHG,点E,B的对应点分别为点G,H.
①当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.如图②,猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若AB=5,BE=4,直接写出四边形AMNQ的面积.
解:(1)四边形AECF为矩形.
理由如下:∵AE⊥BC,CF⊥AD,∴∠AEC=90°,∠AFC=90°,
∵四边形ABCD为菱形,∴AD∥BC,∴∠AFC+∠ECF=180°,∴∠ECF=180°-∠AFC=90°,∴四边形AECF为矩形;
(2)①CH=MD.理由如下:∵四边形ABCD为菱形,∴AB=AD,∠B=∠D.∵△ABE旋转得到△AHG,∴AB=AH,∠B=∠H,∴AH=AD,∠H=∠D.
∵∠HAM=∠DAC,∴△HAM≌△DAC(ASA),∴AM=AC,
∴AH-AC=AD-AM,∴CH=MD;
类型二 与折叠有关
(2023.26)
例2 (2022北部湾)【探究与证明】折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.
【动手操作】如图①,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为B′,E′,展平纸片,连接AB′,BB′,BE′.请完成:
(1)观察图①中∠1,∠2和∠3,试猜想这三个角的大小关系;
解:(1)∠1=∠2=∠3;
(2)证明(1)中的猜想;
证明:设AM,EF交于点O,
由题意得EF是AB的垂直平分线,AM是BB′的垂直平分线,AB=AB′,∴AB′=BB′,OA=OB=OB′,∴AB′=BB′=AB,O为△ABB′的外心,∴∠ABB′=60°,∴∠1=∠2=30°.
∵四边形ABCD是矩形,∴∠ABC=90°,∴∠3=90°-60°=30°,∴∠1=∠2=∠3;
【类比操作】如图②,N为矩形纸片ABCD的边AD上的一点,连接BN,在AB上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕EF;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为B′,P′,展平纸片,连接BB′,P′B′.请完成:
(3)求证:BB′是∠NBC的一条三等分线.
证明:如图,设l与EF交于点O,连接OP′,OP,OB,PB′,同理(2)得OB=OB′=OP=OP′,BP′=PB′=BB′,∴∠P′BO=∠B′BO,∠OBB′=∠BB′O,
∵EF∥BC,∴∠OB′B=∠B′BC,∴∠P′BO=∠B′BO=∠B′BC,∴BB′是∠NBC的一条三等分线.
【思路引导】设AM,EF交于点O,可推出点O是等边三角形ABB′的外心,从而得出∠1和∠2的度数,进一步得出结论;
【思路引导】设l与EF交于点O,连接OP′,OP,OB,PB′.同理(2)可得OB=OB′=OP=OP′,BP′=PB′=BB′,从而得几组相等的角,根据EF∥BC得出一组等角,等量代换即可得证.
3.(2024钦州一模)【问题情境】如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,该怎么办呢?
【实践探究】小西进行了以下操作研究(如图①):
第1步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平.
第2步:再次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到了线段BN.
小雅在小西研究的基础上,再次动手操作(如图②).
(1)直接写出BE和BN的数量关系:________________;
(2)请求出∠ABM的度数;
(3)求证:四边形BGHM是菱形.
(3)证明:由(1)(2)知∠NBM=∠ABM=30°,
∵四边形ABCD是矩形,∴AD∥BC,∠A=∠ABC=90°,∴∠CBN=30°,∴∠MBN=∠CBN=30°.由翻折可知∠BNM=∠A=90°,∴∠BNM=∠BNG=90°,∵BN=BN,
∴△BNM≌△BNG(ASA),∴BM=BG,
∵AD∥BC,∴∠BHM=∠CBN=30°,∴∠BHM=∠MBN=30°,
∴BM=HM,∴BG=HM,∵AD∥BC,
∴四边形BGHM是平行四边形,
∵BM=HM,∴四边形BGHM是菱形.
(1)证明:∵四边形ABCD是正方形,∴AB=DA,∠ABE=90°=∠DAQ,∴∠QAO+∠OAD=90°,
∵AE⊥DQ,∴∠ADO+∠OAD=90°,∴∠QAO=∠ADO,
∴△ABE≌△DAQ(ASA),∴AE=DQ.
∵DQ⊥AE,GF⊥AE,∴DQ∥GF,∵FQ∥DG,∴四边形DQFG是平行四边形,∴GF=DQ,∵AE=DQ,∴AE=FG;
类型三 与动点有关
(北部湾5年2考)
例3 (2022北部湾)已知∠MON=α,点A,B分别在射线OM,ON上运动,AB=6.
(1)如图①,若α=90°,取AB中点D,点A,B运动时,点D也随之运动,点A,B,D的对应点分别为A′,B′,D′,连接OD,OD′.判断OD与OD′有什么样的数量关系?证明你的结论;
(2)如图②,若α=60°,以AB为斜边在其右侧作等腰直角三角形ABC,求点O与点C的最大距离;
(3)如图③,若α=45°,当点A,B运动到什么位置时,△AOB的面积最大?请说明理由,并求出△AOB面积的最大值.
【思路引导】根据“直角三角形斜边中线等于斜边一半”分别求出OD,OD′的长,进而得出结论;
【思路引导】作△AOB的外接圆⊙I,观察图形,找出点O与点C距离最大时,点O′的位置,结合已知条件进而求得结果;
【思路引导】作等腰直角三角形AIB,以点I为圆心,AI长为半径作⊙I,取AB的中点C,连接CI并延长交⊙I于点O,此时△AOB的面积最大,进一步求得结果.
5.(2024广西模拟)【探究与证明】学校开展艺术作品展示活动,九年级数学兴趣小组制作菱形木质框架时(如图①),通过平移支架开展数学探究,探索数学奥秘.
【动手操作】菱形框架固定不动,在AC上平移支架∠EGF的顶点G.
如图①,在菱形ABCD中,已知∠B=∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.
如图②,当顶点G运动到与点A重合时,观察图中EC,CF和BC,试猜想这三条线段之间的数量关系,并证明你的猜想;
6.(2024贵州)如图,∠AOB=90°,点P在∠AOB的平分线上,PA⊥OA于点A.
【操作判断】
(1)如图①,过点P作PC⊥OB于点C,根据题意在图①中画出PC,图中∠APC的度数为______度;
【问题探究】
(2)如图②,点M在线段AO上,连接PM,过点P作PN⊥PM交射线OB于点N,求证:OM+ON=2PA;
(1)解:如图①,PC即为所求;90;
(2)证明:如图②,过P作PC⊥OB于点C.
由(1)知四边形OAPC是矩形,
∵点P在∠AOB的平分线上,PA⊥OA,PC⊥OB,∴PA=PC,∴矩形OAPC是正方形,∴OA=AP=PC=OC,∠APC=90°,
∵PN⊥PM,∴∠APM=∠CPN=90°-∠MPC,
又∠MAP=∠NCP=90°,AP=CP,∴△APM≌△CPN(ASA),
∴AM=CN,∴OM+ON=OM+OC+CN=OM+AM+OC=OA+OC=2AP,∴OM+ON=2PA;
【拓展应用】
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,BF,如图③.已知AC=6,设AD=x,四边形CDFE的面积为y.
①求y与x的函数表达式,并求出y的最小值;
②当BF=2时,请直接写出AD的长度.
同课章节目录
