专题四 阅读理解题 课件(共30张PPT) 2025年中考数学人教版一轮复习考点探究(广西)
文档属性
| 名称 | 专题四 阅读理解题 课件(共30张PPT) 2025年中考数学人教版一轮复习考点探究(广西) |  | |
| 格式 | pptx | ||
| 文件大小 | 950.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 18:59:31 | ||
图片预览










文档简介
(共30张PPT)
数 学
专题四 阅读理解题
类型一 与切线有关的证明与计算
(2024.24,2023.23,北部湾5年4考)
【方法指导】解题方法类阅读理解题会先提出一个问题,并针对这个问题进行拓展延伸,一般这类问题都会用到同一种解题方法或数学思想.一般解题步骤如下:
(1)阅读材料内容,理解答题过程,总结提炼数学思想方法;
(2)模仿材料方法、思路解决问题;
(3)找结构:寻找不变的结构,利用不变结构的特征解决问题.
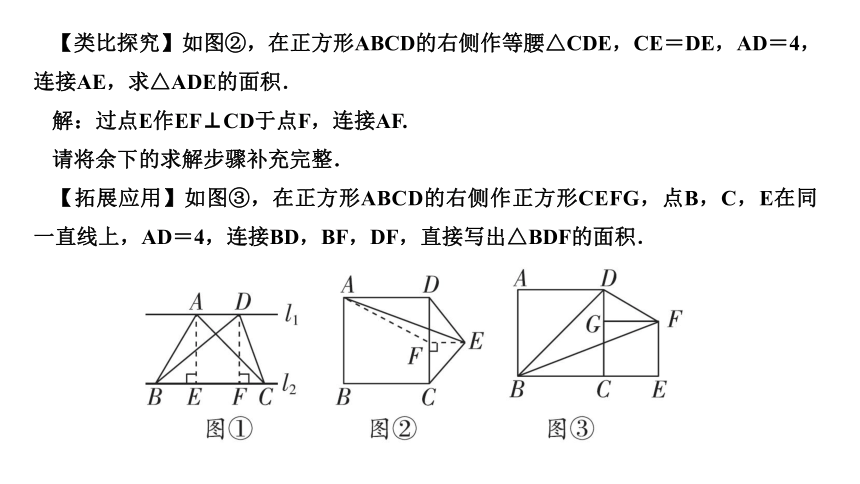
【类比探究】如图②,在正方形ABCD的右侧作等腰△CDE,CE=DE,AD=4,连接AE,求△ADE的面积.
解:过点E作EF⊥CD于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图③,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,AD=4,连接BD,BF,DF,直接写出△BDF的面积.
2.(2024兰州)【观察发现】劳动人民在生产生活中创造了很多取材简单又便于操作的方法,正如木匠刘师傅的“木条画直角法”.如图①,他用木条能快速画出一个以点A为顶点的直角,具体作法如下:
①木条的两端分别记为点M,N,先将木条的端点M与点A重合,任意摆放木条后,另一个端点N的位置记为点B,连接AB;
②木条的端点N固定在点B处,将木条绕点B顺时针旋转一定的角度,端点M的落点记为点C(点A,B,C不在同一条直线上);
③连接CB并延长,将木条沿点C到点B的方向平移,使得端点M与点B重合,端点N在CB延长线上的落点记为点D;
④用另一根足够长的木条画线,连接AD,AC,则画出的∠DAC是直角.
【操作体验】
(1)根据“观察发现”中的信息重现刘师傅的画法.如图②,BA=BC.请画出以A为顶点的直角,记作∠DAC;
【推理论证】
(2)如图①,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB=BC=BD,∴△ABC与△ABD是等腰三角形,
∴∠BCA=∠BAC,∠BDA=∠BAD,(_依据1 )
∴∠BCA+∠BDA=∠BAC+∠BAD=∠DAC.
∵∠DAC+∠BCA+∠BDA=180°,( 依据2)
∴2∠DAC=180°,∴∠DAC=90°.
依据1:________________________________,
依据2:________________________________;
等边对等角(等腰三角形的性质)
三角形内角和定理
【拓展探究】
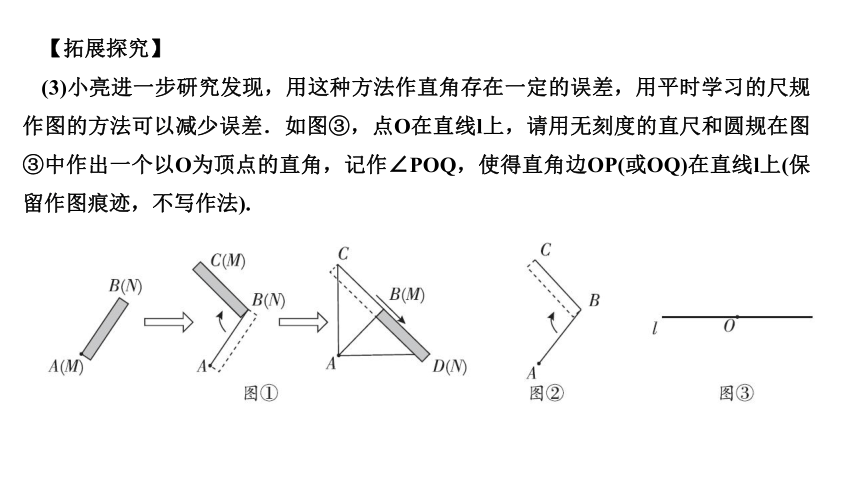
(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差.如图③,点O在直线l上,请用无刻度的直尺和圆规在图③中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上(保留作图痕迹,不写作法).
解:(1)画出以A为顶点的直角∠DAC如解图所示;
(3)画图如解图所示.
3.阅读下面方框内的内容,并完成相应的任务.
任务:
(1)不等式x2-x-6<0的解集为________________;
(2)3种方法都运用了____的数学思想方法(从下面选项中选1个序号即可);
A.分类讨论 B.转化思想 C.特殊到一般 D.数形结合
(3)请你根据方法3的思路,画出函数图象的简图,并结合图象作出解答.
-2<x<3
D
类型二 新定义类
【方法指导】新定义类阅读理解题
(1)读懂题目,搜集信息,理解本质;
(2)新定义题型一般与其他知识结合较多;
(3)熟练掌握和运用数学的常用思想方法,利用数形结合、类比等数学思想解决问题。
4.(2024河南节选)在学习特殊四边形的过程中,我们积累了一定的研究经验.请运用已有经验,对“邻等对补四边形”进行研究.
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
【操作判断】
(1)用分别含有30°和45°角的直角三角形纸板拼出如下图所示的4个四边形,其中是邻等对补四边形的有______(填序号);
②④
【性质探究】
(2)根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图,四边形ABCD是邻等对补四边形,AB=AD,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若BC=m,DC=n,∠BCD=2θ,求AC的长(用含m,n,θ的式子表示).
解:(2)①∠ACD=∠ACB.理由如下:如图,延长CB至点E,使BE=DC,连接AE,
∵四边形ABCD是邻等对补四边形,∴∠ABC+∠D=180°,
∵∠ABC+∠ABE=180°,∴∠ABE=∠D,
∵AB=AD,∴△ABE≌△ADC(SAS),∴∠E=∠ACD,AE=AC,∴∠E=∠ACB,∴∠ACD=∠ACB;
5.(2024盐城)如图①,E,F,G,H分别是 ABCD各边的中点,连接AF,CE交于点M,连接AG,CH交于点N,将四边形AMCN称为 ABCD的“中顶点四边形”.
(1)求证:中顶点四边形AMCN为平行四边形;
(2)①连接AC,BD交于点O,如图②,可得M,N两点都在BD上,当 ABCD满足______________时,中顶点四边形AMCN是菱形;
②已知矩形AMCN为某平行四边形的中顶点四边形,如图③,请用无刻度的直尺和圆规作出该平行四边形(保留作图痕迹,不写作法).
AC⊥BD
类型三 数学文化类
【方法指导】解题的关键在于能否从题目中提取出解题所需的信息,尤其需要注意数学概念、数字、单位、公式等.
6.(2024齐齐哈尔节选)如图①,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图②,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
AB=DE
类型四 项目式学习
7.(2024烟台)根据收集的素材,探索完成任务.
数 学
专题四 阅读理解题
类型一 与切线有关的证明与计算
(2024.24,2023.23,北部湾5年4考)
【方法指导】解题方法类阅读理解题会先提出一个问题,并针对这个问题进行拓展延伸,一般这类问题都会用到同一种解题方法或数学思想.一般解题步骤如下:
(1)阅读材料内容,理解答题过程,总结提炼数学思想方法;
(2)模仿材料方法、思路解决问题;
(3)找结构:寻找不变的结构,利用不变结构的特征解决问题.
【类比探究】如图②,在正方形ABCD的右侧作等腰△CDE,CE=DE,AD=4,连接AE,求△ADE的面积.
解:过点E作EF⊥CD于点F,连接AF.
请将余下的求解步骤补充完整.
【拓展应用】如图③,在正方形ABCD的右侧作正方形CEFG,点B,C,E在同一直线上,AD=4,连接BD,BF,DF,直接写出△BDF的面积.
2.(2024兰州)【观察发现】劳动人民在生产生活中创造了很多取材简单又便于操作的方法,正如木匠刘师傅的“木条画直角法”.如图①,他用木条能快速画出一个以点A为顶点的直角,具体作法如下:
①木条的两端分别记为点M,N,先将木条的端点M与点A重合,任意摆放木条后,另一个端点N的位置记为点B,连接AB;
②木条的端点N固定在点B处,将木条绕点B顺时针旋转一定的角度,端点M的落点记为点C(点A,B,C不在同一条直线上);
③连接CB并延长,将木条沿点C到点B的方向平移,使得端点M与点B重合,端点N在CB延长线上的落点记为点D;
④用另一根足够长的木条画线,连接AD,AC,则画出的∠DAC是直角.
【操作体验】
(1)根据“观察发现”中的信息重现刘师傅的画法.如图②,BA=BC.请画出以A为顶点的直角,记作∠DAC;
【推理论证】
(2)如图①,小亮尝试揭示此操作的数学原理,请你补全括号里的证明依据:
证明:∵AB=BC=BD,∴△ABC与△ABD是等腰三角形,
∴∠BCA=∠BAC,∠BDA=∠BAD,(_依据1 )
∴∠BCA+∠BDA=∠BAC+∠BAD=∠DAC.
∵∠DAC+∠BCA+∠BDA=180°,( 依据2)
∴2∠DAC=180°,∴∠DAC=90°.
依据1:________________________________,
依据2:________________________________;
等边对等角(等腰三角形的性质)
三角形内角和定理
【拓展探究】
(3)小亮进一步研究发现,用这种方法作直角存在一定的误差,用平时学习的尺规作图的方法可以减少误差.如图③,点O在直线l上,请用无刻度的直尺和圆规在图③中作出一个以O为顶点的直角,记作∠POQ,使得直角边OP(或OQ)在直线l上(保留作图痕迹,不写作法).
解:(1)画出以A为顶点的直角∠DAC如解图所示;
(3)画图如解图所示.
3.阅读下面方框内的内容,并完成相应的任务.
任务:
(1)不等式x2-x-6<0的解集为________________;
(2)3种方法都运用了____的数学思想方法(从下面选项中选1个序号即可);
A.分类讨论 B.转化思想 C.特殊到一般 D.数形结合
(3)请你根据方法3的思路,画出函数图象的简图,并结合图象作出解答.
-2<x<3
D
类型二 新定义类
【方法指导】新定义类阅读理解题
(1)读懂题目,搜集信息,理解本质;
(2)新定义题型一般与其他知识结合较多;
(3)熟练掌握和运用数学的常用思想方法,利用数形结合、类比等数学思想解决问题。
4.(2024河南节选)在学习特殊四边形的过程中,我们积累了一定的研究经验.请运用已有经验,对“邻等对补四边形”进行研究.
定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.
【操作判断】
(1)用分别含有30°和45°角的直角三角形纸板拼出如下图所示的4个四边形,其中是邻等对补四边形的有______(填序号);
②④
【性质探究】
(2)根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质.
如图,四边形ABCD是邻等对补四边形,AB=AD,AC是它的一条对角线.
①写出图中相等的角,并说明理由;
②若BC=m,DC=n,∠BCD=2θ,求AC的长(用含m,n,θ的式子表示).
解:(2)①∠ACD=∠ACB.理由如下:如图,延长CB至点E,使BE=DC,连接AE,
∵四边形ABCD是邻等对补四边形,∴∠ABC+∠D=180°,
∵∠ABC+∠ABE=180°,∴∠ABE=∠D,
∵AB=AD,∴△ABE≌△ADC(SAS),∴∠E=∠ACD,AE=AC,∴∠E=∠ACB,∴∠ACD=∠ACB;
5.(2024盐城)如图①,E,F,G,H分别是 ABCD各边的中点,连接AF,CE交于点M,连接AG,CH交于点N,将四边形AMCN称为 ABCD的“中顶点四边形”.
(1)求证:中顶点四边形AMCN为平行四边形;
(2)①连接AC,BD交于点O,如图②,可得M,N两点都在BD上,当 ABCD满足______________时,中顶点四边形AMCN是菱形;
②已知矩形AMCN为某平行四边形的中顶点四边形,如图③,请用无刻度的直尺和圆规作出该平行四边形(保留作图痕迹,不写作法).
AC⊥BD
类型三 数学文化类
【方法指导】解题的关键在于能否从题目中提取出解题所需的信息,尤其需要注意数学概念、数字、单位、公式等.
6.(2024齐齐哈尔节选)如图①,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图②,在△ABC中,∠A=90°,将线段BC绕点B顺时针旋转90°得到线段BD,作DE⊥AB交AB的延长线于点E.
AB=DE
类型四 项目式学习
7.(2024烟台)根据收集的素材,探索完成任务.
同课章节目录
