专题一 函数的实际应用 课件(共22张PPT) 2025年中考数学人教版一轮复习考点探究(广西)
文档属性
| 名称 | 专题一 函数的实际应用 课件(共22张PPT) 2025年中考数学人教版一轮复习考点探究(广西) |

|
|
| 格式 | pptx | ||
| 文件大小 | 595.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-13 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
数 学
专题一 函数的实际应用
类型一 构建函数关系解决实际问题
(北部湾5年4考)
1.(2024眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业篷勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
3.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
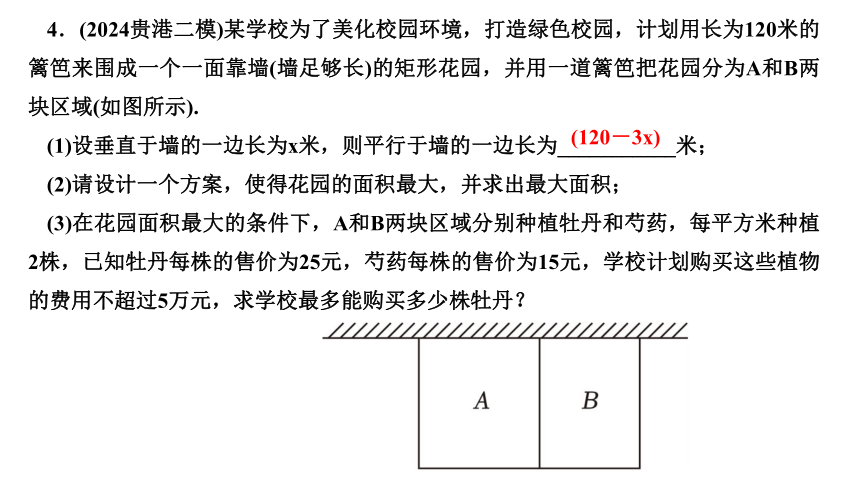
4.(2024贵港二模)某学校为了美化校园环境,打造绿色校园,计划用长为120米的篱笆来围成一个一面靠墙(墙足够长)的矩形花园,并用一道篱笆把花园分为A和B两块区域(如图所示).
(1)设垂直于墙的一边长为x米,则平行于墙的一边长为___________米;
(2)请设计一个方案,使得花园的面积最大,并求出最大面积;
(3)在花园面积最大的条件下,A和B两块区域分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株的售价为25元,芍药每株的售价为15元,学校计划购买这些植物的费用不超过5万元,求学校最多能购买多少株牡丹?
(120-3x)
解:(2)设围成的矩形面积为S平方米,
则S=x(120-3x)=-3x2+120x=-3(x-20)2+1200,
∵-3<0,∴当x=20时,S取最大值1200,
∴当垂直于墙的一边长为20米时,花园面积最大,最大面积为1200平方米;
(3)设购买牡丹m株,则购买芍药1200×2-m=(2400-m)株,∵学校计划购买费用不超过5万元,∴25m+15(2400-m)≤50000,解得m≤1400,∴最多可以购买1400株牡丹.
类型二 抛物线型问题
(北部湾2021.24)
(1)若火箭第二级的引发点的高度为3.6 km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离;
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
7.城市绿化部门定期安排洒水车为公路两侧绿化带浇水.
信息1:洒水车沿着平行于公路路牙方向行驶,喷水口H离地面竖直高度OH=1.5 m.
信息2:可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3 m,竖直高度EF=0.5 m.内边缘抛物线y2是由外边缘抛物线y1向左平移得到,外缘边抛物线y1最高点A离喷水口的水平距离为2 m,高出喷水口0.5 m.
【问题解决】
任务1:确定浇灌方式
(1)求外边缘抛物线y1的函数解析式,并求喷出水的最大射程OC;
(2)直接写出内边缘抛物线y2与x轴正半轴的交点B的坐标;
任务2:提倡有效浇灌
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,求OD的取值范围.
数 学
专题一 函数的实际应用
类型一 构建函数关系解决实际问题
(北部湾5年4考)
1.(2024眉山)眉山是“三苏”故里,文化底蕴深厚.近年来眉山市旅游产业篷勃发展,促进了文创产品的销售,某商店用960元购进的A款文创产品和用780元购进的B款文创产品数量相同.每件A款文创产品进价比B款文创产品进价多15元.
(1)求A,B两款文创产品每件的进价各是多少元?
(2)已知A款文创产品每件售价为100元,B款文创产品每件售价为80元,根据市场需求,商店计划再用不超过7400元的总费用购进这两款文创产品共100件进行销售,问:怎样进货才能使销售完后获得的利润最大,最大利润是多少元?
3.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
(1)求y与x的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
4.(2024贵港二模)某学校为了美化校园环境,打造绿色校园,计划用长为120米的篱笆来围成一个一面靠墙(墙足够长)的矩形花园,并用一道篱笆把花园分为A和B两块区域(如图所示).
(1)设垂直于墙的一边长为x米,则平行于墙的一边长为___________米;
(2)请设计一个方案,使得花园的面积最大,并求出最大面积;
(3)在花园面积最大的条件下,A和B两块区域分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株的售价为25元,芍药每株的售价为15元,学校计划购买这些植物的费用不超过5万元,求学校最多能购买多少株牡丹?
(120-3x)
解:(2)设围成的矩形面积为S平方米,
则S=x(120-3x)=-3x2+120x=-3(x-20)2+1200,
∵-3<0,∴当x=20时,S取最大值1200,
∴当垂直于墙的一边长为20米时,花园面积最大,最大面积为1200平方米;
(3)设购买牡丹m株,则购买芍药1200×2-m=(2400-m)株,∵学校计划购买费用不超过5万元,∴25m+15(2400-m)≤50000,解得m≤1400,∴最多可以购买1400株牡丹.
类型二 抛物线型问题
(北部湾2021.24)
(1)若火箭第二级的引发点的高度为3.6 km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离;
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
7.城市绿化部门定期安排洒水车为公路两侧绿化带浇水.
信息1:洒水车沿着平行于公路路牙方向行驶,喷水口H离地面竖直高度OH=1.5 m.
信息2:可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3 m,竖直高度EF=0.5 m.内边缘抛物线y2是由外边缘抛物线y1向左平移得到,外缘边抛物线y1最高点A离喷水口的水平距离为2 m,高出喷水口0.5 m.
【问题解决】
任务1:确定浇灌方式
(1)求外边缘抛物线y1的函数解析式,并求喷出水的最大射程OC;
(2)直接写出内边缘抛物线y2与x轴正半轴的交点B的坐标;
任务2:提倡有效浇灌
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,求OD的取值范围.
同课章节目录
