第2章 二次函数—最值问题 专题训练 (含详解)2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 第2章 二次函数—最值问题 专题训练 (含详解)2024-2025学年北师大版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 00:00:00 | ||
图片预览




文档简介
2024-2025学年北师大版九年级数学下册《第2章二次函数—最值问题》专题训练(附答案)
一、单选题
1.二次函数的最小值是( )
A.3 B.2 C.1 D.-1
2.已知二次函数,当时,函数y的最大值为( )
A.1 B.3 C.9 D.19
3.二次函数 (其中x是自变量且), 当时, y随x的增大而增大,且时,y的最大值是,则m的值为( )
A. B. C.或6 D.6
4.如图,在中,,若点为直线左侧一点,当时,则的最大值为( )
A. B. C. D.
5.如图,一块矩形木板,长,宽,小虎将一块等腰直角三角板的一条直角边靠在顶点上,另一条直角边与边交于点,三角板的直角顶点在边上移动(不含端点),当线段最短时,的长为( )
A. B. C. D.
6.如图,矩形中,,E为边上一个动点,连接,取的中点G,点G绕点E逆时针旋转得到点F,连接,则面积的最小值是( )
A.4 B. C.3 D.
7.我们定义一种新函数:形如的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥函数的图象如图所示,则下列结论正确的是( )
A.
B.当时,函数的最大值是8
C.当时,直线与该图象恰有三个公共点
D.关于x的方程的所有实数根的和为3
8.二次函数()的部分图象如图所示,对称轴为直线,且经过点.下列说法∶①;②;③;④ 若,是抛物线上的两点,则;⑤.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.已知二次函数的图象的最低点在x轴上,则 .
10.已知二次函数,当时,的最大值是16,最小值是8,则 .
11.在数学课上,老师要求同学们将一个关于字母的二次三项式(、是常数)配成(是常数)的形式,则的最小值是 .
12.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则飞机着陆后滑行的最长时间为 秒.
13.已知二次函数
(1)若则函数的最大值为 .
(2)若当时,的最大值为5,则的值为 .
14.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为 .
15.如果关于x的一元二次方程的两个实数根分别为,,,那么y的最小值为 .
16.如图,P为抛物线上第一象限内的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形的周长的最大值为
三、解答题
17.在二次函数中.
(1)若它的图象过点,则的值为多少?
(2)当时,的最小值为,求出的值.
(3)如果,,都在这个二次函数的图象上,且求的取值范围.
18.已知二次函数.
(1)当,时,
①求该函数图象的顶点坐标.
②当时,求x的取值范围.
(2)当时,y的最小值为;当时,y的最小值为3,求二次函数的表达式.
19.如图,有长为的篱笆,一面利用墙(墙的最大可利用长度为),围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.
(1)求S与x的函数关系式;
(2)如果要围成面积为的花圃,的长是多少m;
(3)当的长是多少m时,S取得最大值,最大值是多少?
20.牛肉干是内蒙古的特产,被誉为“成吉思汗的行军粮”.某超市销售一款牛肉干,每袋进价150元,售价170元,平均每月可售出200袋.为了提高利润,该超市决定涨价销售,经调查,每袋涨价1元时,平均每月可少卖出2袋.
(1)当该款牛肉干每袋涨价多少元时,当月利润最大
(2)若超市要求该款牛肉干每月盈利不低于5400元,求每袋牛肉干售价的取值范围.
21.阅读下面的例题及点拨,并解决问题:
【例题】
有一块三角形余料,它的边,高.要把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,问加工成的正方形零件的边长是多少毫米
【点拨】:解四边形为正方形,
,
,
设正方形零件的边长为xmm,则,.
∵,
,即,
解得.故这个正方形零件的边长是.
【
问题探究】
(1)如果原题中要加工成的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图①,此时,这个矩形零件的两条边长是多少?
(2)如果原题中所要加工成的零件只是一个矩形,如图②,求这个矩形面积的最大值和达到这个最大值时矩形零件的两条边长.
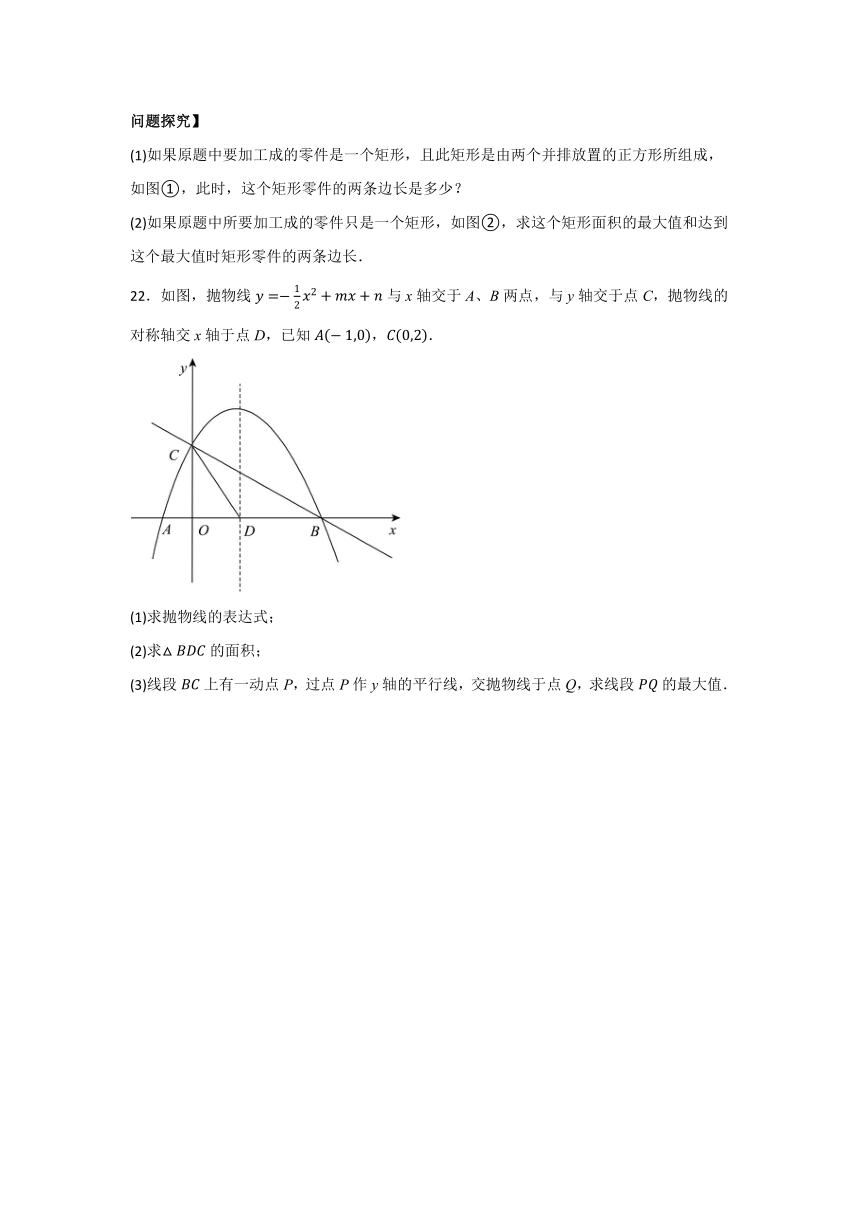
22.如图,抛物线与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知,.
(1)求抛物线的表达式;
(2)求的面积;
(3)线段上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段的最大值.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B D D B D B C B
1.解:,
所以有最小值,最小值是2.
故选:B.
2.解:由题意得:二次函数的对称轴为直线,
∵,函数图象开口向上,
又
∴当时,函数有最大值,此时,
故选:D
3.解:∵二次函数,
∴该函数的对称轴为直线,
∵当时,y随x的增大而增大,
∴,
又∵当时,y的最大值为,
∴时,,
即,
解得,,(舍去),
故选:D.
4.解:∵,
∴,
∴,
∵在中,,
∴,
∴,
∴,
∴,
∴当时,有最大值,
故选:B.
5.解:设,则,
∵四边形是矩形,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴
∵,
∴当时,y有最小值,
∴线段最短时,的长为,
故选:D.
6.解:过点F作的垂线交的延长线于点H,
∵矩形中,,点G绕点E逆时针旋转得到点F,
∴,
∴,,
∴,
∵的中点G,
∴,
∴,
设,,
∴,,,
∴
故面积的最小值为,
故选B.
7.解:∵,是函数图象和x轴的交点,
∴,
解得:,
∴,
故A错误;
由图象可得,函数没有最大值,故B错误;
如图,当时,直线,
当时,,当时,,则,
即直线,与x轴交于点,与y轴交于点,如图,
此时直线与该图象恰有三个公共点,
故C正确;
关于x的方程,即或,
当时,,
当时,,
∴关于x的方程的所有实数根的和为,故D错误,
故选:C.
8.解:∵二次函数()的部分图象如图所示,对称轴为直线,且经过点,
∴,,
,即,
,
∴,
,
∴①错误,②正确,
∴,
∴③正确,,
∴,
∵对称轴为直线,图象开口向下,
∴当,函数取最大值,即离顶点越远函数值越小,
∴,
,
,即,故⑤正确,
∵,是抛物线上的两点,
∴离顶点更近,
∴,故④错误,
∴正确的结论有②③⑤这个,
故选:B.
9.解:∵二次函数的图象的最低点在x轴上
∴且,
整理得,且,
解得,(舍去),
故答案为:2.
10.解:∵,
∴抛物线的顶点为,对称轴为直线,
当时,抛物线开口向下,当时,的最大值是16,最小值是8,
∴当时,的最大值是,
当时,的最小值是,
∴,
解得
∴,
当时,抛物线开口向上,当时,的最大值是16,最小值是8,
∴当时,的最大值是,
当时,的最小值是,
∴,
解得
∴,
综上可知,,
故答案为:12
11.解: 是关于字母的二次三项式,
,
,
,
,
,
,
当时,有最小值,最小值为,
故答案为:.
12.解:
,
,
当的时候,滑行的距离最长,
故飞机着陆后滑行的最长时间为秒,
故答案为:20.
13.解:(1)当时,该二次函数为,
∵,
∴当时,y有最大值,最大值为.
故答案为:;
(2)∵,
∴该二次函数的对称轴为直线.
当时,抛物线开口向上,
∴当时,y随x的增大而减小,当时,y随x的增大而增大.
∵x轴上到的距离比到的距离大,
∴当时,y有最大值,
∴,
解得:;
当时,抛物线开口向下,
∴当时,y有最大值,最大值为,
∴,
解得:.
综上可知a的值为或.
故答案为:1或.
14.解:二次函数y=x2+ax+4以y轴为对称轴
,即 ,
二次函数解析式为 ,
点P(m,n)在二次函数y=x2+ax+4的图象上,
,
,
m-n的最大值为 .
故答案为:.
15.解:∵关于x的一元二次方程的两个实数根分别为,,
∴
解得
∴,
∴
∵
∴抛物线开口向上,对称轴为
∴当时,y随m的增大而增大
∴时y的最小值为.
故答案为:.
16.解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值12.
故答案为:12.
17.(1)解:将点代入函数解析式得,
,
解得.
(2)解:因为抛物线的对称轴为直线,且抛物线的开口向上,
所以当时,
,
解得舍负.
当时,
,
解得舍去,
所以的值为.
(3)解:由,两点纵坐标相等可知,
,
即,
将点坐标代入函数解析式得,
,
又∵,
∴ ,
解得,
所以,
∵,
∴点离抛物线的对称轴比点离抛物线的对称轴近,
则,
当时,
,
解得,
当时,
,
解得,
综上所述,的取值范围是或.
18.(1)解:①当,时,解析式为,
该函数的顶点坐标为;
②抛物线,开口向上,对称轴为直线,
当时,即,
解不等式得:或,
(2)∵二次函数开口向上,当时,y的最小值为3,
∴时,,
∵当时,y的最小值为;
∴时,,代入得:
,
,
∴,
∵对称轴在y轴左侧,a、b同号,,
∴,
故抛物线解析式为:.
19.(1)解: 宽,则长,
,
又,且,
,
关于x的函数解析式为.
(2)解:当时,即,
整理得:,解得:或,
,
,
当为时,面积为;
(3)解:由(1)知:,
,对称轴,开口向下,
当时,S最大,最大值.
答:当的长是米时,围成的花圃的面积最大,最大面积是平方米.
20.解:(1)设该款牛肉干每袋涨价x元,当月利润为y元.
根据题意可得,
,
当时,y最大,
答:该款牛肉干每袋涨价40元时,当月利润最大.
(2)由(1)知,,
解得,,
,
当时,利润不低于5400元,
此时,,
答:每袋牛肉干售价不低于180元不高于240元.
21.(1)解:设,则,
由题意知,
,
即,
解得,
,
故这个矩形零件的两条边长是,;
(2)解:设,矩形的面积为,
由题意知,
,
即,
解得,
,
的最大值为,此时,.
22.解:(1)抛物线与x轴交于A,B两点,与y轴交于点C,,.
∴,
解得:,
故抛物线解析式为:;
(2)∵,,
∴,,
∵对称轴为 ,
∴ ,,
∴,
∴,
∴;
(3)令,则,
解得,,
∴,
设直线的解析式为,代入得:
,
解得,
∴直线的解析式为,
设,则,
则,
此时的最大值为2.
一、单选题
1.二次函数的最小值是( )
A.3 B.2 C.1 D.-1
2.已知二次函数,当时,函数y的最大值为( )
A.1 B.3 C.9 D.19
3.二次函数 (其中x是自变量且), 当时, y随x的增大而增大,且时,y的最大值是,则m的值为( )
A. B. C.或6 D.6
4.如图,在中,,若点为直线左侧一点,当时,则的最大值为( )
A. B. C. D.
5.如图,一块矩形木板,长,宽,小虎将一块等腰直角三角板的一条直角边靠在顶点上,另一条直角边与边交于点,三角板的直角顶点在边上移动(不含端点),当线段最短时,的长为( )
A. B. C. D.
6.如图,矩形中,,E为边上一个动点,连接,取的中点G,点G绕点E逆时针旋转得到点F,连接,则面积的最小值是( )
A.4 B. C.3 D.
7.我们定义一种新函数:形如的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥函数的图象如图所示,则下列结论正确的是( )
A.
B.当时,函数的最大值是8
C.当时,直线与该图象恰有三个公共点
D.关于x的方程的所有实数根的和为3
8.二次函数()的部分图象如图所示,对称轴为直线,且经过点.下列说法∶①;②;③;④ 若,是抛物线上的两点,则;⑤.其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
9.已知二次函数的图象的最低点在x轴上,则 .
10.已知二次函数,当时,的最大值是16,最小值是8,则 .
11.在数学课上,老师要求同学们将一个关于字母的二次三项式(、是常数)配成(是常数)的形式,则的最小值是 .
12.飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则飞机着陆后滑行的最长时间为 秒.
13.已知二次函数
(1)若则函数的最大值为 .
(2)若当时,的最大值为5,则的值为 .
14.点P(m,n)在以y轴为对称轴的二次函数y=x2+ax+4的图象上,则m-n的最大值为 .
15.如果关于x的一元二次方程的两个实数根分别为,,,那么y的最小值为 .
16.如图,P为抛物线上第一象限内的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形的周长的最大值为
三、解答题
17.在二次函数中.
(1)若它的图象过点,则的值为多少?
(2)当时,的最小值为,求出的值.
(3)如果,,都在这个二次函数的图象上,且求的取值范围.
18.已知二次函数.
(1)当,时,
①求该函数图象的顶点坐标.
②当时,求x的取值范围.
(2)当时,y的最小值为;当时,y的最小值为3,求二次函数的表达式.
19.如图,有长为的篱笆,一面利用墙(墙的最大可利用长度为),围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.
(1)求S与x的函数关系式;
(2)如果要围成面积为的花圃,的长是多少m;
(3)当的长是多少m时,S取得最大值,最大值是多少?
20.牛肉干是内蒙古的特产,被誉为“成吉思汗的行军粮”.某超市销售一款牛肉干,每袋进价150元,售价170元,平均每月可售出200袋.为了提高利润,该超市决定涨价销售,经调查,每袋涨价1元时,平均每月可少卖出2袋.
(1)当该款牛肉干每袋涨价多少元时,当月利润最大
(2)若超市要求该款牛肉干每月盈利不低于5400元,求每袋牛肉干售价的取值范围.
21.阅读下面的例题及点拨,并解决问题:
【例题】
有一块三角形余料,它的边,高.要把它加工成正方形零件,使正方形的一边在上,其余两个顶点分别在上,问加工成的正方形零件的边长是多少毫米
【点拨】:解四边形为正方形,
,
,
设正方形零件的边长为xmm,则,.
∵,
,即,
解得.故这个正方形零件的边长是.
【
问题探究】
(1)如果原题中要加工成的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图①,此时,这个矩形零件的两条边长是多少?
(2)如果原题中所要加工成的零件只是一个矩形,如图②,求这个矩形面积的最大值和达到这个最大值时矩形零件的两条边长.
22.如图,抛物线与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知,.
(1)求抛物线的表达式;
(2)求的面积;
(3)线段上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段的最大值.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B D D B D B C B
1.解:,
所以有最小值,最小值是2.
故选:B.
2.解:由题意得:二次函数的对称轴为直线,
∵,函数图象开口向上,
又
∴当时,函数有最大值,此时,
故选:D
3.解:∵二次函数,
∴该函数的对称轴为直线,
∵当时,y随x的增大而增大,
∴,
又∵当时,y的最大值为,
∴时,,
即,
解得,,(舍去),
故选:D.
4.解:∵,
∴,
∴,
∵在中,,
∴,
∴,
∴,
∴,
∴当时,有最大值,
故选:B.
5.解:设,则,
∵四边形是矩形,
∴,
∵,
∴,,
∴,
∴,
∴,
∴,
∴
∵,
∴当时,y有最小值,
∴线段最短时,的长为,
故选:D.
6.解:过点F作的垂线交的延长线于点H,
∵矩形中,,点G绕点E逆时针旋转得到点F,
∴,
∴,,
∴,
∵的中点G,
∴,
∴,
设,,
∴,,,
∴
故面积的最小值为,
故选B.
7.解:∵,是函数图象和x轴的交点,
∴,
解得:,
∴,
故A错误;
由图象可得,函数没有最大值,故B错误;
如图,当时,直线,
当时,,当时,,则,
即直线,与x轴交于点,与y轴交于点,如图,
此时直线与该图象恰有三个公共点,
故C正确;
关于x的方程,即或,
当时,,
当时,,
∴关于x的方程的所有实数根的和为,故D错误,
故选:C.
8.解:∵二次函数()的部分图象如图所示,对称轴为直线,且经过点,
∴,,
,即,
,
∴,
,
∴①错误,②正确,
∴,
∴③正确,,
∴,
∵对称轴为直线,图象开口向下,
∴当,函数取最大值,即离顶点越远函数值越小,
∴,
,
,即,故⑤正确,
∵,是抛物线上的两点,
∴离顶点更近,
∴,故④错误,
∴正确的结论有②③⑤这个,
故选:B.
9.解:∵二次函数的图象的最低点在x轴上
∴且,
整理得,且,
解得,(舍去),
故答案为:2.
10.解:∵,
∴抛物线的顶点为,对称轴为直线,
当时,抛物线开口向下,当时,的最大值是16,最小值是8,
∴当时,的最大值是,
当时,的最小值是,
∴,
解得
∴,
当时,抛物线开口向上,当时,的最大值是16,最小值是8,
∴当时,的最大值是,
当时,的最小值是,
∴,
解得
∴,
综上可知,,
故答案为:12
11.解: 是关于字母的二次三项式,
,
,
,
,
,
,
当时,有最小值,最小值为,
故答案为:.
12.解:
,
,
当的时候,滑行的距离最长,
故飞机着陆后滑行的最长时间为秒,
故答案为:20.
13.解:(1)当时,该二次函数为,
∵,
∴当时,y有最大值,最大值为.
故答案为:;
(2)∵,
∴该二次函数的对称轴为直线.
当时,抛物线开口向上,
∴当时,y随x的增大而减小,当时,y随x的增大而增大.
∵x轴上到的距离比到的距离大,
∴当时,y有最大值,
∴,
解得:;
当时,抛物线开口向下,
∴当时,y有最大值,最大值为,
∴,
解得:.
综上可知a的值为或.
故答案为:1或.
14.解:二次函数y=x2+ax+4以y轴为对称轴
,即 ,
二次函数解析式为 ,
点P(m,n)在二次函数y=x2+ax+4的图象上,
,
,
m-n的最大值为 .
故答案为:.
15.解:∵关于x的一元二次方程的两个实数根分别为,,
∴
解得
∴,
∴
∵
∴抛物线开口向上,对称轴为
∴当时,y随m的增大而增大
∴时y的最小值为.
故答案为:.
16.解:设点P的坐标为,,
由题意可知:四边形的周长,
∴,
当时,C有最大值12.
故答案为:12.
17.(1)解:将点代入函数解析式得,
,
解得.
(2)解:因为抛物线的对称轴为直线,且抛物线的开口向上,
所以当时,
,
解得舍负.
当时,
,
解得舍去,
所以的值为.
(3)解:由,两点纵坐标相等可知,
,
即,
将点坐标代入函数解析式得,
,
又∵,
∴ ,
解得,
所以,
∵,
∴点离抛物线的对称轴比点离抛物线的对称轴近,
则,
当时,
,
解得,
当时,
,
解得,
综上所述,的取值范围是或.
18.(1)解:①当,时,解析式为,
该函数的顶点坐标为;
②抛物线,开口向上,对称轴为直线,
当时,即,
解不等式得:或,
(2)∵二次函数开口向上,当时,y的最小值为3,
∴时,,
∵当时,y的最小值为;
∴时,,代入得:
,
,
∴,
∵对称轴在y轴左侧,a、b同号,,
∴,
故抛物线解析式为:.
19.(1)解: 宽,则长,
,
又,且,
,
关于x的函数解析式为.
(2)解:当时,即,
整理得:,解得:或,
,
,
当为时,面积为;
(3)解:由(1)知:,
,对称轴,开口向下,
当时,S最大,最大值.
答:当的长是米时,围成的花圃的面积最大,最大面积是平方米.
20.解:(1)设该款牛肉干每袋涨价x元,当月利润为y元.
根据题意可得,
,
当时,y最大,
答:该款牛肉干每袋涨价40元时,当月利润最大.
(2)由(1)知,,
解得,,
,
当时,利润不低于5400元,
此时,,
答:每袋牛肉干售价不低于180元不高于240元.
21.(1)解:设,则,
由题意知,
,
即,
解得,
,
故这个矩形零件的两条边长是,;
(2)解:设,矩形的面积为,
由题意知,
,
即,
解得,
,
的最大值为,此时,.
22.解:(1)抛物线与x轴交于A,B两点,与y轴交于点C,,.
∴,
解得:,
故抛物线解析式为:;
(2)∵,,
∴,,
∵对称轴为 ,
∴ ,,
∴,
∴,
∴;
(3)令,则,
解得,,
∴,
设直线的解析式为,代入得:
,
解得,
∴直线的解析式为,
设,则,
则,
此时的最大值为2.
