贵州省黔东南苗族侗族自治州2024-2025学年上学期期中调研八年级数学试卷(含答案)
文档属性
| 名称 | 贵州省黔东南苗族侗族自治州2024-2025学年上学期期中调研八年级数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 833.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 21:13:41 | ||
图片预览



文档简介
2024—2025学年度第一学期期中调研八年级数学试卷
(本试卷三个大题, 25个小题,时间120分,总分150分)
学号 班级 姓名 成绩
一、选择题(共12题,每小题3分,共36分)
1.下列四个手机APP图标中,是轴对称图形的是( )
A B C D
2.下列长度的三条线段能组成三角形的是( )
A. 3,4,8 B. 5,6,11 C. 1,2,3 D. 5,6,10
3.如图,△ACF≌△BDE,点A、B、C、D在同一条直线上,下列结论中错误的是( )
A.AF∥BE B.∠ACF=∠DBE C.AB=CD D.CF∥DE
4.如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A.等边三角形 B.等腰直角三角形 C.等腰三角形 D.含30°角的直角三角形
5.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
如图,在△ABC中,AC=BC,点D在AC边上,点E在CB的延长线上,DE与AB相
交于点F,若∠C=50°,∠E=25°,则∠BFE的度数为( )
A.30° B.40° C.50° D.60°
7.如图,D、E分别是BC、AC的中点,,则的面积为( ).
A.4 B. 8 C. 10 D. 12
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB
于E,垂足为D.如果CE=12,则ED的长为( )
A.3 B.4 C.5 D.6
9.如图,度.
A.180 B.270 C.360 D.54
10.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的
坐标为(-6,3),则点B的坐标为 ( )
A.(3,3) B.(3,4) C.(2,4) D.(1,4)
11.如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE.动
点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的
运动时间为秒,当△ABP 和△DCE 全等时,的值为 ( )
A.1 B.1或3 C.1或7 D.3或7
12.如图,在△ABC中,AB=AC,BC=4,面积是10.AB的垂直
平分线ED分别交AC,AB边于E、D两点, 若点F为BC
边的中点,点P为线段ED上一动点,则△PBF周长的最小
值为( ).
A.5 B.7 C.10 D.14
二、填空题(每小4分,共16分)
13.如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,
其中不能确定△ABC≌△DCB的是 (只填序号).
如图,∠AOB=300,OC平分∠AOB,P为OC上任意一点,PD∥OA
交OB于D,PE⊥OA于E,若OD=8,则PE的长为 。
15.如图,将一张长方形纸片ABCD按图中那样折叠,若AE=6,AB=8,
BE=10,则重叠部分的面积是 .
16.如图,C为线段AE上一动点(不与点A,E重合),
在AE同侧分别作正三角形ABC和正三角形CDE,AD与
BC交于点P,BE与CD交于点Q,连接PQ。以下五个结论:
①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOB=600,
其中正确的结论有 (只要把序号填上).
三、解答题(9个小题,共98分,解答应写出必要的说明,证明或演算步骤)
17.(10分)已知一个多边形的内角和是它的外角和的3倍,则它是几边形?
有多少条对角线?
18.(10分)如图,在平面直角坐标系中,在坐标系中A(1,1),
B(4,2),C(3,4).
在图中画出关于x轴的对称图形,并分别写出对应
点A1、B1、C1的坐标.
(2)求.
(3)在y轴上是否存在一点p,使得AP+CP最小,若存在,
请在图中描出点P,若不存在请说明理由.
19.(10分)已知:如图,AB∥CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:AE=CF.
20.(10分)如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2h后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向上的D处时,又航行了多少海里?
21.(12分) 如图,和都是等边三角形,点在的延长线上.
(1)求证:;求证:. (3)求的度数.
22.(12分)在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以α cm/s(α>0且α≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
(1)若AB=AC,P在线段BC上,求当α为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
23.(12) 如图,已知在△ABC中,AB=AC,D为BC的中点,
过点D作DE⊥AB,DF⊥AC,垂足分别为E,F。
(1)求证:DE=DF;(2)若∠A=60°,BE=1,求△ABC的周长。
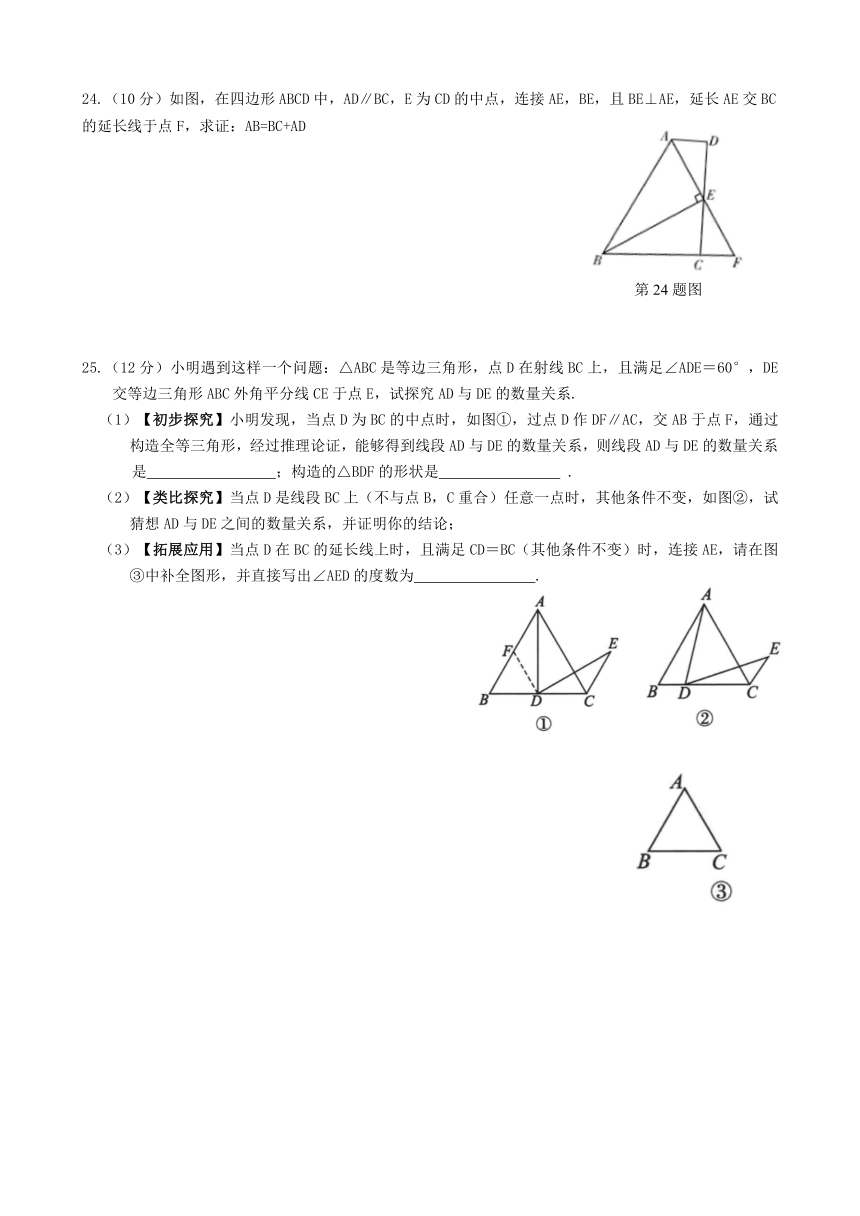
24.(10分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,且BE⊥AE,延长AE交BC的延长线于点F,求证:AB=BC+AD
25.(12分)小明遇到这样一个问题:△ABC是等边三角形,点D在射线BC上,且满足∠ADE=60°,DE交等边三角形ABC外角平分线CE于点E,试探究AD与DE的数量关系.
(1)【初步探究】小明发现,当点D为BC的中点时,如图①,过点D作DF∥AC,交AB于点F,通过构造全等三角形,经过推理论证,能够得到线段AD与DE的数量关系,则线段AD与DE的数量关系
是 ;构造的△BDF的形状是 .
(2)【类比探究】当点D是线段BC上(不与点B,C重合)任意一点时,其他条件不变,如图②,试猜想AD与DE之间的数量关系,并证明你的结论;
(3)【拓展应用】当点D在BC的延长线上时,且满足CD=BC(其他条件不变)时,连接AE,请在图③中补全图形,并直接写出∠AED的度数为 .
2024—2025学年度第一学期期中调研八年级数学试卷
参考答案
一、选择题:(每题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B A A B B D C D C B
二、填空题:(每题4分,共16分)
13. ② ; 14.; 15.40; 16.①②③⑤.
三、解答题:(本题7个小题,共70分)
17.(10分)解:设这个多边形的边数为n,则 ……(1分
(n-2)×180=360×3……(4分)
解得n=8 ……(6分)
对角线有(条) ............9分
∴这个多边形的边数是8,对角线有20条.(10分)
18.(10分)(1)作图正确……(2分)
A1(1,-1),B1(4,-2)C1(3,-4)……(5分);
(2)S△……(8分)
(3)作A(或C)的对称点A2或C2,连接A2C或AC2交Y轴于P点.……(10分)
19.(10分)证明∵DEAC,BFAC,
∴∠AFB=∠CED, ……(2分)
又∵AB∥CD
∴∠A=∠C ……(4分)
在△AFB与△CED中
∴△AFB≌△CED(AAS)
∴AF=CE ……(8分)
∴AF-EF=CE-EF,∴AE=CF ……(10分)
(10分)解:∵∠CBD=600,∠BAC=300,
∴∠BCA=∠BAC=300,................2分
∴BC=BA=,.................4分
又CD⊥AD,
∴∠CDB=900,........................6分
∴∠BCD=300,........................8分
∴BD= (海里),
答:又航行了20海里...............10分.
21.(12分)(1)证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60° ……(3分)
∴∠BAC-∠DAC=∠DAE-∠DAC
∴∠BAD=∠CAE ……(4分)
在△ABD与△CAE中
∴△BAD≌△CAE(SAS) ……(6分)
(2)∵△BAD≌△CAE, ∴BD=CE ……(7分)
又△ADE是等边三角形, ∴DE=AE ……(8分)
又BD+DE=BE,∴AE+CE=BE. ……(9分)
(3)∵△ADE是等边三角形,∴∠ADE=∠AED=60° ……(10分)
∴∠ADB=120°,又∵△BAD≌△CAE,∴∠ADB=∠AEC=120°……(11分)
∴∠BEC=60°……(12分) ……(12分)
22.(12分)解:(1)由题意,得BP=2,PC=16-2, ……(1分)
∵AB=AC,∴∠B=∠C, ……(2分)
又点P与点Q同时出发,但速度不同, ∴ ……(3分)
∴当BP=CP,BD=CQ时, △BPD≌△CQP,则
2=16-2,解得. ……(4分)
又点D是AB的中点,∴CQ=BD=10,∴4a=10,解得a=2.5 (cm/s) ……(6分)
(2)分两种情况讨论:
①当∠BPD=90°时,又∠B=60°,∴∠BDP=30°
∴……(9分)
②当∠BDP=90°时,又∠B=60°,∴∠BPD=30°
∴……(11分)
∴出发2.5S或10S时,△BPD为直角三角形.……(12分)
23.(12分)(1)证明:连接AD................1分
∵AB=AC,点D为BC的中点,
∴AD平分∠BAC,..............4分
又DE⊥AB,DF⊥AC,
∴DE=DF..............6分.
∵AB=AC,∠A=600,
∴△ABC是等边三角形,........8分
∴AB=AC=BC,∠B=600,
又DE⊥AB ,
∴∠BED=900,.............9分
∴∠BDE=300,
∴BD=,..........10分
又D是BC的中点,
∴BC=4,..................11分
∴△ABC的周长为.........12分.
24.(12分)证明:∵E为CD的中点,
∴DE=CE,……(2分)
又AD∥BC,
∴∠ADE=∠FCE,∠DAEE=∠CFE,............4分
在△ADE与△FCE中
∴△ADE≌△FCE (AAS),
∴AE=FE,AD=FC,。................6分
又BE⊥AE,
∴AB=BF,...............................8分
又AB=BF=BC+CF................9分
∴AB=BC+AD....................................10分.
25.(12分)(1)AD=DE,△BDF是等边三角形;..........4分.
(2) AD=DE,..........................................5分
过点D作DF∥AC,
∴∠BFD=∠BAC,∠BDF=∠ACB, ……6分
又△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=600,AB=BC
∴∠BFD=∠BDF=∠ABC=600,
∴△BDF是等边三角形,.............7分
∴BD=BF,∠BFD=600,
∴AB-BF=BC-BD ,∠AFD=1200,
∴AF=DC,
又∠ADC=600+∠EDC=600+∠DAF,
∴∠DAF=∠EDC,
又CE是等边△ABC的外角平分线,
∴∠ACE=600,
∴∠AFD=∠DCE=1200,...........8分
在△AFD与△DCE中
∴△AFD≌△DCE(ASA)
∴AD=DE,.................9分
(3)600...............................12分。
理由:略
(本试卷三个大题, 25个小题,时间120分,总分150分)
学号 班级 姓名 成绩
一、选择题(共12题,每小题3分,共36分)
1.下列四个手机APP图标中,是轴对称图形的是( )
A B C D
2.下列长度的三条线段能组成三角形的是( )
A. 3,4,8 B. 5,6,11 C. 1,2,3 D. 5,6,10
3.如图,△ACF≌△BDE,点A、B、C、D在同一条直线上,下列结论中错误的是( )
A.AF∥BE B.∠ACF=∠DBE C.AB=CD D.CF∥DE
4.如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A.等边三角形 B.等腰直角三角形 C.等腰三角形 D.含30°角的直角三角形
5.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
如图,在△ABC中,AC=BC,点D在AC边上,点E在CB的延长线上,DE与AB相
交于点F,若∠C=50°,∠E=25°,则∠BFE的度数为( )
A.30° B.40° C.50° D.60°
7.如图,D、E分别是BC、AC的中点,,则的面积为( ).
A.4 B. 8 C. 10 D. 12
8.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB
于E,垂足为D.如果CE=12,则ED的长为( )
A.3 B.4 C.5 D.6
9.如图,度.
A.180 B.270 C.360 D.54
10.如图,在△ACB中,∠ACB=90°,AC=BC,点C的坐标为(-2,0),点A的
坐标为(-6,3),则点B的坐标为 ( )
A.(3,3) B.(3,4) C.(2,4) D.(1,4)
11.如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE.动
点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的
运动时间为秒,当△ABP 和△DCE 全等时,的值为 ( )
A.1 B.1或3 C.1或7 D.3或7
12.如图,在△ABC中,AB=AC,BC=4,面积是10.AB的垂直
平分线ED分别交AC,AB边于E、D两点, 若点F为BC
边的中点,点P为线段ED上一动点,则△PBF周长的最小
值为( ).
A.5 B.7 C.10 D.14
二、填空题(每小4分,共16分)
13.如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB,③AB=DC,
其中不能确定△ABC≌△DCB的是 (只填序号).
如图,∠AOB=300,OC平分∠AOB,P为OC上任意一点,PD∥OA
交OB于D,PE⊥OA于E,若OD=8,则PE的长为 。
15.如图,将一张长方形纸片ABCD按图中那样折叠,若AE=6,AB=8,
BE=10,则重叠部分的面积是 .
16.如图,C为线段AE上一动点(不与点A,E重合),
在AE同侧分别作正三角形ABC和正三角形CDE,AD与
BC交于点P,BE与CD交于点Q,连接PQ。以下五个结论:
①AD=BE;②AP=BQ;③PQ∥AE;④DE=DP;⑤∠AOB=600,
其中正确的结论有 (只要把序号填上).
三、解答题(9个小题,共98分,解答应写出必要的说明,证明或演算步骤)
17.(10分)已知一个多边形的内角和是它的外角和的3倍,则它是几边形?
有多少条对角线?
18.(10分)如图,在平面直角坐标系中,在坐标系中A(1,1),
B(4,2),C(3,4).
在图中画出关于x轴的对称图形,并分别写出对应
点A1、B1、C1的坐标.
(2)求.
(3)在y轴上是否存在一点p,使得AP+CP最小,若存在,
请在图中描出点P,若不存在请说明理由.
19.(10分)已知:如图,AB∥CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
求证:AE=CF.
20.(10分)如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C在北偏西30°方向,轮船航行2h后到达B处,在B处测得灯塔C在北偏西60°方向.当轮船到达灯塔C的正东方向上的D处时,又航行了多少海里?
21.(12分) 如图,和都是等边三角形,点在的延长线上.
(1)求证:;求证:. (3)求的度数.
22.(12分)在△ABC中,AB=20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以α cm/s(α>0且α≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
(1)若AB=AC,P在线段BC上,求当α为何值时,能够使△BPD和△CQP全等?
(2)若∠B=60°,求出发几秒后,△BDP为直角三角形?
23.(12) 如图,已知在△ABC中,AB=AC,D为BC的中点,
过点D作DE⊥AB,DF⊥AC,垂足分别为E,F。
(1)求证:DE=DF;(2)若∠A=60°,BE=1,求△ABC的周长。
24.(10分)如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE,BE,且BE⊥AE,延长AE交BC的延长线于点F,求证:AB=BC+AD
25.(12分)小明遇到这样一个问题:△ABC是等边三角形,点D在射线BC上,且满足∠ADE=60°,DE交等边三角形ABC外角平分线CE于点E,试探究AD与DE的数量关系.
(1)【初步探究】小明发现,当点D为BC的中点时,如图①,过点D作DF∥AC,交AB于点F,通过构造全等三角形,经过推理论证,能够得到线段AD与DE的数量关系,则线段AD与DE的数量关系
是 ;构造的△BDF的形状是 .
(2)【类比探究】当点D是线段BC上(不与点B,C重合)任意一点时,其他条件不变,如图②,试猜想AD与DE之间的数量关系,并证明你的结论;
(3)【拓展应用】当点D在BC的延长线上时,且满足CD=BC(其他条件不变)时,连接AE,请在图③中补全图形,并直接写出∠AED的度数为 .
2024—2025学年度第一学期期中调研八年级数学试卷
参考答案
一、选择题:(每题3分,共36分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D B A A B B D C D C B
二、填空题:(每题4分,共16分)
13. ② ; 14.; 15.40; 16.①②③⑤.
三、解答题:(本题7个小题,共70分)
17.(10分)解:设这个多边形的边数为n,则 ……(1分
(n-2)×180=360×3……(4分)
解得n=8 ……(6分)
对角线有(条) ............9分
∴这个多边形的边数是8,对角线有20条.(10分)
18.(10分)(1)作图正确……(2分)
A1(1,-1),B1(4,-2)C1(3,-4)……(5分);
(2)S△……(8分)
(3)作A(或C)的对称点A2或C2,连接A2C或AC2交Y轴于P点.……(10分)
19.(10分)证明∵DEAC,BFAC,
∴∠AFB=∠CED, ……(2分)
又∵AB∥CD
∴∠A=∠C ……(4分)
在△AFB与△CED中
∴△AFB≌△CED(AAS)
∴AF=CE ……(8分)
∴AF-EF=CE-EF,∴AE=CF ……(10分)
(10分)解:∵∠CBD=600,∠BAC=300,
∴∠BCA=∠BAC=300,................2分
∴BC=BA=,.................4分
又CD⊥AD,
∴∠CDB=900,........................6分
∴∠BCD=300,........................8分
∴BD= (海里),
答:又航行了20海里...............10分.
21.(12分)(1)证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60° ……(3分)
∴∠BAC-∠DAC=∠DAE-∠DAC
∴∠BAD=∠CAE ……(4分)
在△ABD与△CAE中
∴△BAD≌△CAE(SAS) ……(6分)
(2)∵△BAD≌△CAE, ∴BD=CE ……(7分)
又△ADE是等边三角形, ∴DE=AE ……(8分)
又BD+DE=BE,∴AE+CE=BE. ……(9分)
(3)∵△ADE是等边三角形,∴∠ADE=∠AED=60° ……(10分)
∴∠ADB=120°,又∵△BAD≌△CAE,∴∠ADB=∠AEC=120°……(11分)
∴∠BEC=60°……(12分) ……(12分)
22.(12分)解:(1)由题意,得BP=2,PC=16-2, ……(1分)
∵AB=AC,∴∠B=∠C, ……(2分)
又点P与点Q同时出发,但速度不同, ∴ ……(3分)
∴当BP=CP,BD=CQ时, △BPD≌△CQP,则
2=16-2,解得. ……(4分)
又点D是AB的中点,∴CQ=BD=10,∴4a=10,解得a=2.5 (cm/s) ……(6分)
(2)分两种情况讨论:
①当∠BPD=90°时,又∠B=60°,∴∠BDP=30°
∴……(9分)
②当∠BDP=90°时,又∠B=60°,∴∠BPD=30°
∴……(11分)
∴出发2.5S或10S时,△BPD为直角三角形.……(12分)
23.(12分)(1)证明:连接AD................1分
∵AB=AC,点D为BC的中点,
∴AD平分∠BAC,..............4分
又DE⊥AB,DF⊥AC,
∴DE=DF..............6分.
∵AB=AC,∠A=600,
∴△ABC是等边三角形,........8分
∴AB=AC=BC,∠B=600,
又DE⊥AB ,
∴∠BED=900,.............9分
∴∠BDE=300,
∴BD=,..........10分
又D是BC的中点,
∴BC=4,..................11分
∴△ABC的周长为.........12分.
24.(12分)证明:∵E为CD的中点,
∴DE=CE,……(2分)
又AD∥BC,
∴∠ADE=∠FCE,∠DAEE=∠CFE,............4分
在△ADE与△FCE中
∴△ADE≌△FCE (AAS),
∴AE=FE,AD=FC,。................6分
又BE⊥AE,
∴AB=BF,...............................8分
又AB=BF=BC+CF................9分
∴AB=BC+AD....................................10分.
25.(12分)(1)AD=DE,△BDF是等边三角形;..........4分.
(2) AD=DE,..........................................5分
过点D作DF∥AC,
∴∠BFD=∠BAC,∠BDF=∠ACB, ……6分
又△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=600,AB=BC
∴∠BFD=∠BDF=∠ABC=600,
∴△BDF是等边三角形,.............7分
∴BD=BF,∠BFD=600,
∴AB-BF=BC-BD ,∠AFD=1200,
∴AF=DC,
又∠ADC=600+∠EDC=600+∠DAF,
∴∠DAF=∠EDC,
又CE是等边△ABC的外角平分线,
∴∠ACE=600,
∴∠AFD=∠DCE=1200,...........8分
在△AFD与△DCE中
∴△AFD≌△DCE(ASA)
∴AD=DE,.................9分
(3)600...............................12分。
理由:略
同课章节目录
