北师大版九年级数学下册课件:3.3垂径定理(共22张PPT)
文档属性
| 名称 | 北师大版九年级数学下册课件:3.3垂径定理(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-16 00:00:00 | ||
图片预览




文档简介
课件22张PPT。3.3 垂径定理义务教育教科书(北师)九年级数学下册
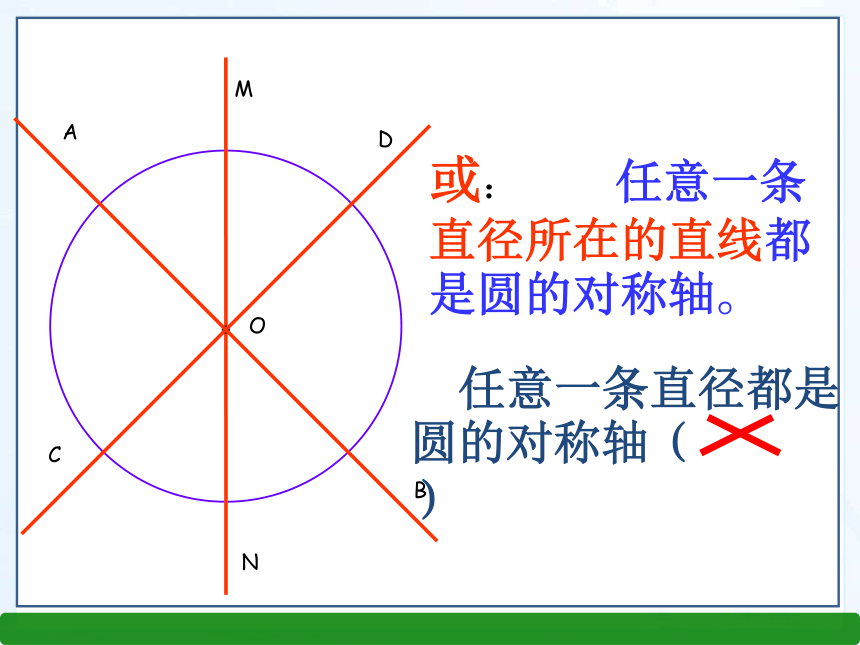
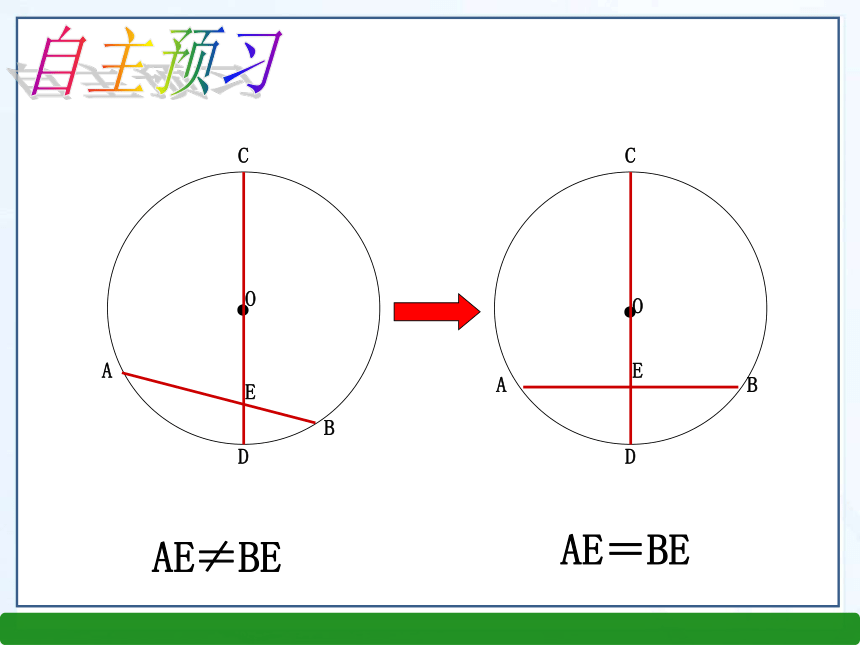
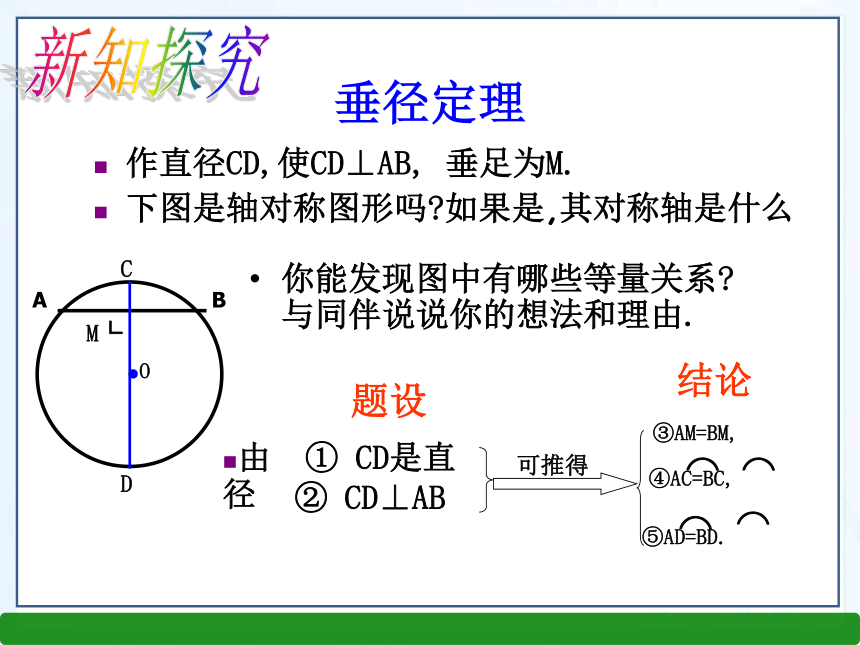
第三章 圆1、什么是轴对称图形?我们在直线形中学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。如线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形圆是轴对称图形吗? 如果是,它的对称轴是什么?你能找到多少条对称轴?知识回顾圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可利用折叠的方法即可解决上述问题.情境引入OACBNMD或: 任意一条直径所在的直线都是圆的对称轴。 任意一条直径都是圆的对称轴( )AE≠BEAE=BE自主预习③AM=BM,垂径定理你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB, 垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么由 ① CD是直径② CD⊥AB题设结论新知探究如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,⌒⌒AC和BC重合,垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
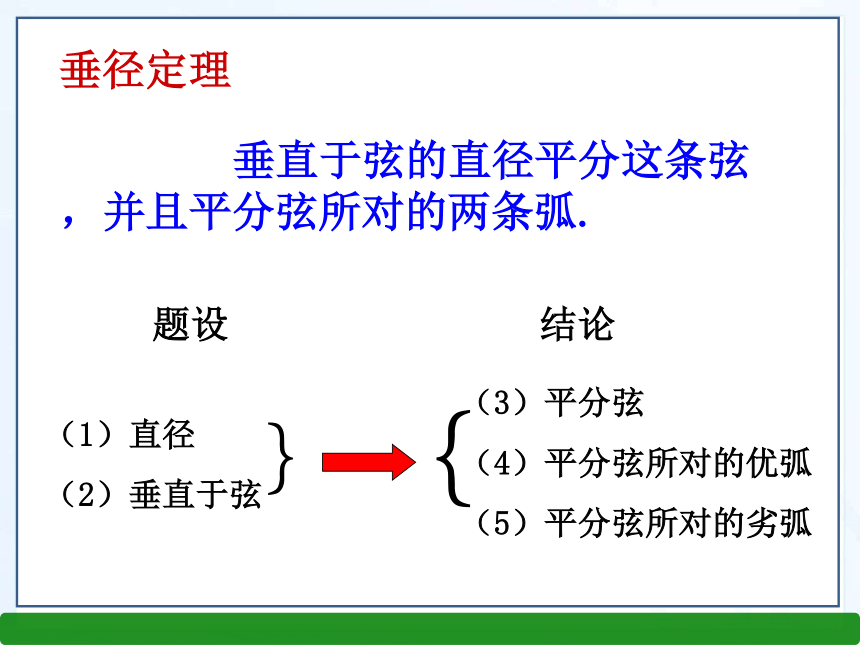
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
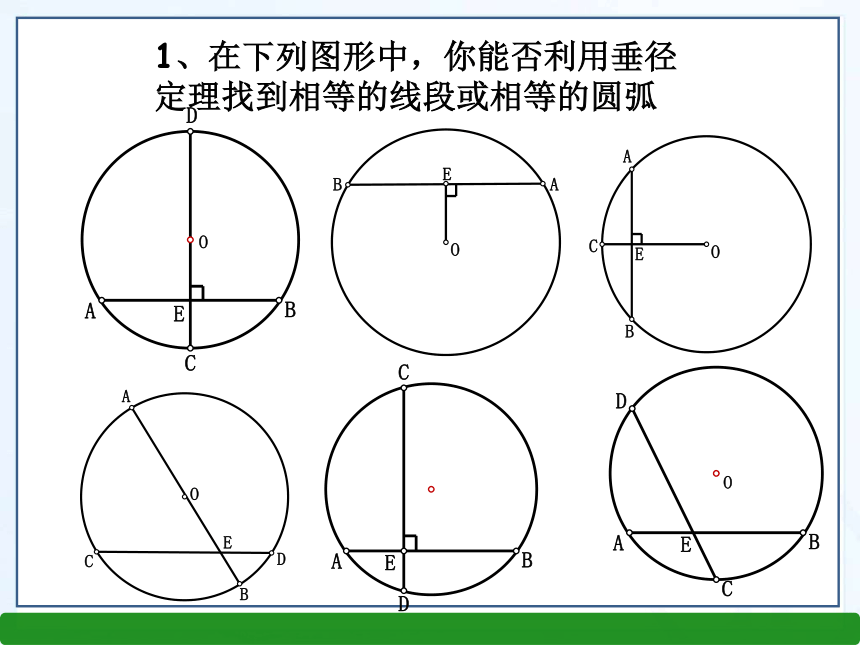
(5)平分弦所对的劣弧1、在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧 2、如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E解:连结OA. 过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ∴AE=4厘米
在Rt △AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米MOACBN①直线MN过圆心③ AC=BC
②MN⊥AB
④弧AM=弧BM ⑤弧AN=弧BN探索一:结论:OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CD你可以写出相应的命题吗?如图,在下列五个条件中:只要具备其中两个条件,
就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂径定理的逆定理垂径定理及逆定理垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,③ AM=BM,② CD⊥AB,⌒⌒④AC=BC,⌒⌒⑤AD=BD.CDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点 画一画你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:1、判断⑴垂直于弦的直线平分弦,并且平分弦所对的弧( )⑵弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )⑶圆的不与直径垂直的弦必不被这条直径平分 ( )⑷平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )⑸圆内两条非直径的弦不能互相平分( )×√××√随堂练习(6)平分弦的直径,平分这条弦所对的弧。(7)平分弦的直线,必定过圆心。(8)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???挑战自我 填一填(9)弦的垂直平分线一定是圆的直径.⑽平分弧的直线,平分这条弧所对的弦. ⑾弦垂直于直径,这条直径就被弦平分.???挑战自我 填一填3、已知:如图,⊙O 中, AB为 弦,C 为 弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.挑战自我 做一做
垂径定理及其推论1的实质是把
(1)直线MN过圆心;
(2)直线MN垂直AB; (3)直线MN平分AB;
(4)直线MN平分弧AMB; (5)直线MN平分弧ANB
中的两个条件进行了四种组合,分别推出了其余的三个结论.这样的组合还有六种,由于时间有限,课堂上未作进一步的推导,同学们课下不妨试一试. 知识梳理
第三章 圆1、什么是轴对称图形?我们在直线形中学过哪些轴对称图形? 如果一个图形沿一条直线对折,直线两旁的部分能够互相重合,那么这个图形叫轴对称图形。如线段、角、等腰三角形、矩形、菱形、等腰梯形、正方形圆是轴对称图形吗? 如果是,它的对称轴是什么?你能找到多少条对称轴?知识回顾圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可利用折叠的方法即可解决上述问题.情境引入OACBNMD或: 任意一条直径所在的直线都是圆的对称轴。 任意一条直径都是圆的对称轴( )AE≠BEAE=BE自主预习③AM=BM,垂径定理你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CD⊥AB, 垂足为M.下图是轴对称图形吗?如果是,其对称轴是什么由 ① CD是直径② CD⊥AB题设结论新知探究如图,小明的理由是:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM,∴Rt△OAM≌Rt△OBM.∴AM=BM.∴点A和点B关于CD对称.∵⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,⌒⌒AC和BC重合,垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.题设结论(1)直径
(2)垂直于弦}{(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧1、在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧 2、如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。E解:连结OA. 过O作OE⊥AB,垂足为E,
则OE=3厘米,AE=BE。
∵AB=8厘米 ∴AE=4厘米
在Rt △AOE中,根据勾股定理有OA=5厘米 ∴⊙O的半径为5厘米MOACBN①直线MN过圆心③ AC=BC
②MN⊥AB
④弧AM=弧BM ⑤弧AN=弧BN探索一:结论:OABMN一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论1. (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。CD你可以写出相应的命题吗?如图,在下列五个条件中:只要具备其中两个条件,
就可推出其余三个结论.① CD是直径,③ AM=BM,② CD⊥AB,垂径定理的逆定理垂径定理及逆定理垂直于弦的直径平分弦,并且平分弦所的两条弧.平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧. 垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.① CD是直径,③ AM=BM,② CD⊥AB,⌒⌒④AC=BC,⌒⌒⑤AD=BD.CDABE例:平分已知弧AB已知:弧AB
作法:⒈ 连结AB.⒉作AB的垂直平分线 CD,交弧AB于点E.点E就是所求弧AB的中点。求作:弧AB的中点 画一画你能破镜重圆吗?ABACmn·O 作弦AB.AC及它们的垂直平分线m.n,交于O点;以O为圆心,OA为半径作圆。破镜重圆ABCmn·O 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
作图依据:1、判断⑴垂直于弦的直线平分弦,并且平分弦所对的弧( )⑵弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )⑶圆的不与直径垂直的弦必不被这条直径平分 ( )⑷平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )⑸圆内两条非直径的弦不能互相平分( )×√××√随堂练习(6)平分弦的直径,平分这条弦所对的弧。(7)平分弦的直线,必定过圆心。(8)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???挑战自我 填一填(9)弦的垂直平分线一定是圆的直径.⑽平分弧的直线,平分这条弧所对的弦. ⑾弦垂直于直径,这条直径就被弦平分.???挑战自我 填一填3、已知:如图,⊙O 中, AB为 弦,C 为 弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.挑战自我 做一做
垂径定理及其推论1的实质是把
(1)直线MN过圆心;
(2)直线MN垂直AB; (3)直线MN平分AB;
(4)直线MN平分弧AMB; (5)直线MN平分弧ANB
中的两个条件进行了四种组合,分别推出了其余的三个结论.这样的组合还有六种,由于时间有限,课堂上未作进一步的推导,同学们课下不妨试一试. 知识梳理
