2016春华师大版九年级数学下册课件:28.2 用样本估计总体(共22张PPT)
文档属性
| 名称 | 2016春华师大版九年级数学下册课件:28.2 用样本估计总体(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 647.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-17 00:00:00 | ||
图片预览






文档简介
课件22张PPT。义务教育教科书(华师)九年级数学下册
第28章 样本与总体28.2 用样本估计总体 在上节课中,我们知道在选取样本时应注意:
1、所选取的样本必须具有代表性,
2、所选取的样本的容量应该足够大,这样的样本才能反映总体的特性,所选取的样本才比较可靠. 知识回顾 为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.
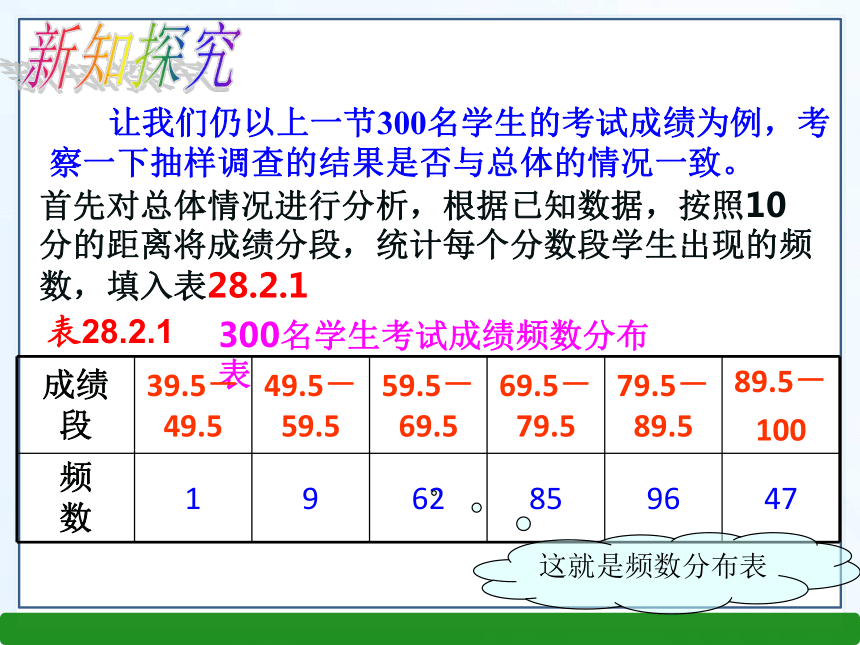
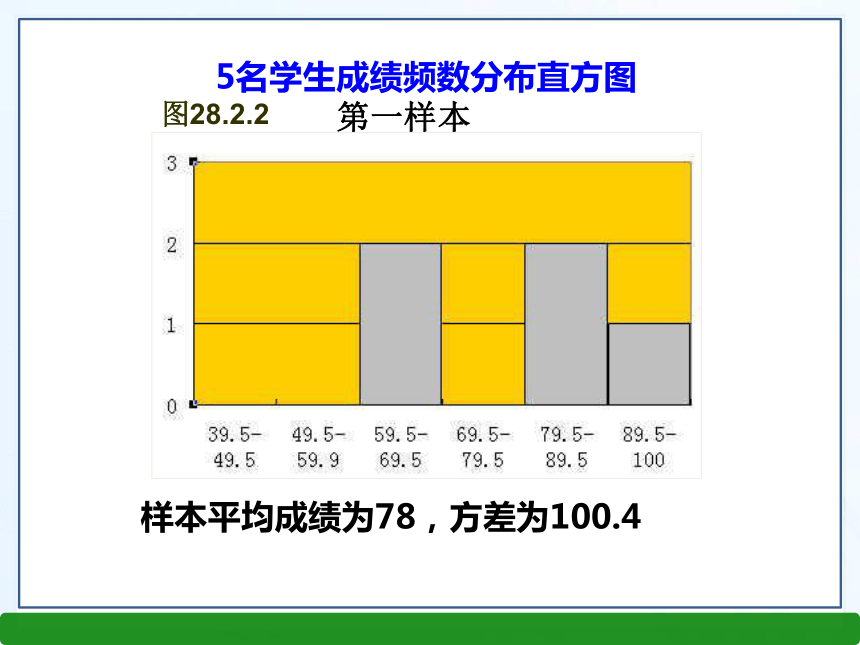
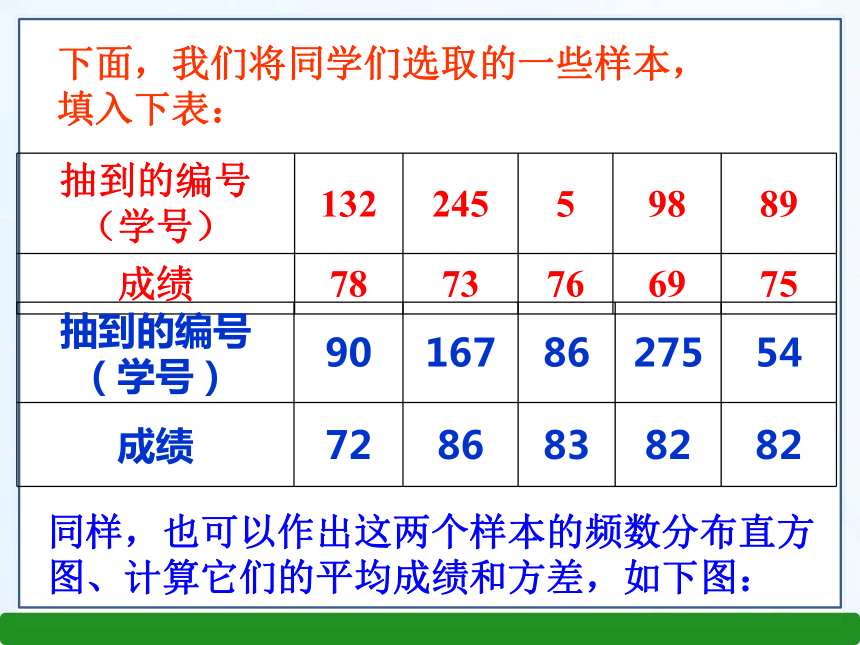
例如,可以在2 000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生. 新知探究整理概念 简单的随机抽样就是用抽签的方法决定哪些个体进入样本,统计学家称这种理想的抽样方法为简单随机抽样. 让我们仍以上一节300名学生的考试成绩为例,考察一下抽样调查的结果是否与总体的情况一致。首先对总体情况进行分析,根据已知数据,按照10分的距离将成绩分段,统计每个分数段学生出现的频数,填入表28.2.1300名学生考试成绩频数分布表这就是频数分布表表28.2.1 新知探究根据上表绘制直方图 (图28.2.1)300名学生成绩频数分布直方图总体的平均成绩为78.1,方差为116.3 从图表中可以清楚地看出79.5分到89.5分这个分数段的学生数最多,90分以上的同学较少,不及格的学生数最少。 这就是频数分布直方图 活动1中,我们用简单的随机抽样方法,已经得到了第一个样本,这5个随机数如下表(表28.2.2): 图28.2.2是这个样本的频数分布直方图、平均成绩和方差。样本平均成绩为78,方差为100.4图28.2.2下面,我们将同学们选取的一些样本,
填入下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和方差,如下图: 样本平均成绩为:80.8,
方差为:42.25样本平均成绩为:74.2,
方差为:14.44 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图图28.2.3 从以上三张图比较来看,它们之间存在明显的差异,平均数和方差与总体的平均数与方差也差异较大,显然这样选择的样本不能反映总体的特性,是不可靠的。什么原因呢?样本平均成绩为79.7,方差为88.41 让我们再用大一些的样本试一试,这次每个样本含有10个个体。图28.2.410名学生成绩频数分布直方图第一样本10名学生成绩频数分布直方图第二样本图28.2.4 我们继续用随机抽样方法,重复上述步骤,再取第二个样本。图28.2.4是根据小明取到的样本数据得到的频数分布直方图。样本平均成绩为83.3,方差为132.61 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和方差似乎比较接近总体的平均成绩78.1和方差116.3。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。图28.2.5是根据小明取到的两个样本数据得到的频数分布直方图。样本平均成绩为75.65,方差为103.5275 图28.2.540名学生成绩频数分布直方图第二样本样本平均成绩为77.1,方差为114.49 图28.2.5 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和方差与总体的平均成绩和方差的差距更小了!(相当接近总体的平均成绩78.1,方差116.3)你们从自己的抽样过程中是否也得出了同样的结果?样本大更容易认识总体的真面目。另外两个40个个体的样本情况:样本平均成绩为
75.7分,
方差为104.04 样本平均成绩为
77.1分,
方差为114.49 当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的方差相当接近。
一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确,相应地,搜集、整理、计算数据的工作量也就越大,因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小。知识梳理随堂练习 请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与方差,绘制频数分布直方图,并与总体的平均数、方差比较。 课本P92 习题28.2 3题例2.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做上标记,然后放回到湖里,过一段时间待带标记的鱼完全混合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,湖里大约有多少条鱼? 解: 设湖里大约有x条鱼,
则 100:x=20:200
∴x=1000.
答:湖里大约有1000条鱼.评注:本题一方面考查了学生由样本估计总体的思想方法和具体做法,另一 方面考察了学生应用数学的能力,这也是中考命题的一个重要方向.
第28章 样本与总体28.2 用样本估计总体 在上节课中,我们知道在选取样本时应注意:
1、所选取的样本必须具有代表性,
2、所选取的样本的容量应该足够大,这样的样本才能反映总体的特性,所选取的样本才比较可靠. 知识回顾 为了使样本能较好地反映总体情况,除了有合适的样本容量外,抽取时还要尽量使每一个个体有相等的机会被抽到.
例如,可以在2 000名学生的注册学号中,随意抽取100个学号,调查这些学号对应的100名学生. 新知探究整理概念 简单的随机抽样就是用抽签的方法决定哪些个体进入样本,统计学家称这种理想的抽样方法为简单随机抽样. 让我们仍以上一节300名学生的考试成绩为例,考察一下抽样调查的结果是否与总体的情况一致。首先对总体情况进行分析,根据已知数据,按照10分的距离将成绩分段,统计每个分数段学生出现的频数,填入表28.2.1300名学生考试成绩频数分布表这就是频数分布表表28.2.1 新知探究根据上表绘制直方图 (图28.2.1)300名学生成绩频数分布直方图总体的平均成绩为78.1,方差为116.3 从图表中可以清楚地看出79.5分到89.5分这个分数段的学生数最多,90分以上的同学较少,不及格的学生数最少。 这就是频数分布直方图 活动1中,我们用简单的随机抽样方法,已经得到了第一个样本,这5个随机数如下表(表28.2.2): 图28.2.2是这个样本的频数分布直方图、平均成绩和方差。样本平均成绩为78,方差为100.4图28.2.2下面,我们将同学们选取的一些样本,
填入下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和方差,如下图: 样本平均成绩为:80.8,
方差为:42.25样本平均成绩为:74.2,
方差为:14.44 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图图28.2.3 从以上三张图比较来看,它们之间存在明显的差异,平均数和方差与总体的平均数与方差也差异较大,显然这样选择的样本不能反映总体的特性,是不可靠的。什么原因呢?样本平均成绩为79.7,方差为88.41 让我们再用大一些的样本试一试,这次每个样本含有10个个体。图28.2.410名学生成绩频数分布直方图第一样本10名学生成绩频数分布直方图第二样本图28.2.4 我们继续用随机抽样方法,重复上述步骤,再取第二个样本。图28.2.4是根据小明取到的样本数据得到的频数分布直方图。样本平均成绩为83.3,方差为132.61 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和方差似乎比较接近总体的平均成绩78.1和方差116.3。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。图28.2.5是根据小明取到的两个样本数据得到的频数分布直方图。样本平均成绩为75.65,方差为103.5275 图28.2.540名学生成绩频数分布直方图第二样本样本平均成绩为77.1,方差为114.49 图28.2.5 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和方差与总体的平均成绩和方差的差距更小了!(相当接近总体的平均成绩78.1,方差116.3)你们从自己的抽样过程中是否也得出了同样的结果?样本大更容易认识总体的真面目。另外两个40个个体的样本情况:样本平均成绩为
75.7分,
方差为104.04 样本平均成绩为
77.1分,
方差为114.49 当样本中个体太少时,样本的平均数、方差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、方差与总体的方差相当接近。
一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确,相应地,搜集、整理、计算数据的工作量也就越大,因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小。知识梳理随堂练习 请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与方差,绘制频数分布直方图,并与总体的平均数、方差比较。 课本P92 习题28.2 3题例2.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做上标记,然后放回到湖里,过一段时间待带标记的鱼完全混合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,湖里大约有多少条鱼? 解: 设湖里大约有x条鱼,
则 100:x=20:200
∴x=1000.
答:湖里大约有1000条鱼.评注:本题一方面考查了学生由样本估计总体的思想方法和具体做法,另一 方面考察了学生应用数学的能力,这也是中考命题的一个重要方向.
