人教版(2024)数学八年级下册17.1勾股定理 教学设计(表格式)
文档属性
| 名称 | 人教版(2024)数学八年级下册17.1勾股定理 教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 58.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-14 00:00:00 | ||
图片预览

文档简介
《勾股定理》教学设计
课题 《勾股定理》
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析勾股定理:直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理是中学数学重要定理之一,它揭示了直角三角形三边之间的数量关系.由此,在直角三角形中已知任意两边长,就可以求出第三边长.勾股定理常用来求解线段长度或距离问题.勾股定理的探究是从特殊的等腰直角三角形出发,到网格中直角三角形,再到一般的直角三角形,体现了从特殊到一般的探究过程和研究方法.证明勾股定理的关键是利用割补法求以斜边为边长的正方形的面积,并以此引导学生发现证明勾股定理的思路.我国对勾股定理的研究和其他国家相比是比较早的,在国际上得到肯定.要通过我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感;要通过对勾股定理的探索和发现,培养学生学好数学的自信心. 基于以上分析,可以确定本节课的教学重点是:探索并证明勾股定理.
学情分析通过前面的学习,学生已经掌握了全等三角形、直角三角形两锐角互余、完全平方公式等基础知识,积累了通过测量、拼图、折纸来研究几何命题的基本活动经验,这些都为本节课探究和证明勾股定理奠定了基础.学生面对复杂图形的变换,对教材中给出的文字证明还存在一定的理解困难,提出问题的能力、逻辑推理能力还有待提高.
学习目标(1)经历勾股定理的探究过程.了解关于勾股定理的一些文化历史背景,通过对我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感.(2)能用勾股定理解决一些简单问题.
重难点(1)会利用数形结合的思想说明勾股定理。(2)会利用勾股定理求直角三角形的边长。
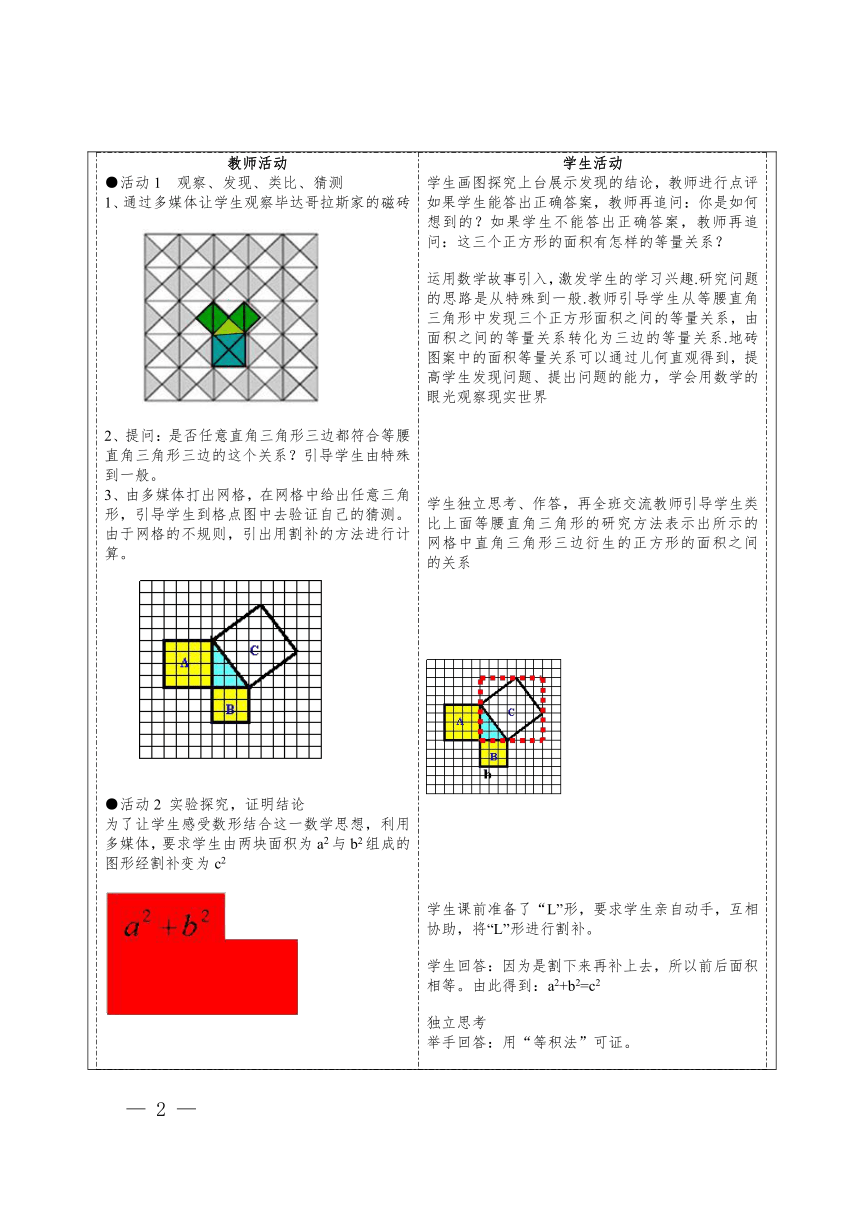
教学评活动过程教师活动学生活动环节一:创设情境温故知新,情境创设引导语:前面我们已经研究了一般的三角形的边、角性质,本节课我们将研究特殊的三角形一一直角三角形.我们研究过直角三角形角的性质,那么直角三角形的三边之间具有怎样的等量关系呢?我们从特殊的直角三角形等腰直角三角形开始研究.学生聆听并思考从三角形的知识体系入手构建研究路径,体现知识之间的上下位关系,唤醒学生头脑中已有的相关知识,直接引入课题,使学生明确学习目标环节二:问题探究教师活动●活动1 观察、发现、类比、猜测1、通过多媒体让学生观察毕达哥拉斯家的磁砖 2、提问:是否任意直角三角形三边都符合等腰直角三角形三边的这个关系?引导学生由特殊到一般。3、由多媒体打出网格,在网格中给出任意三角形,引导学生到格点图中去验证自己的猜测。由于网格的不规则,引出用割补的方法进行计算。 ●活动2 实验探究,证明结论为了让学生感受数形结合这一数学思想,利用多媒体,要求学生由两块面积为a2与b2组成的图形经割补变为c2 提问:由以上过程,你能得到什么结论?由此我们得到了证明勾股定理的一种方法:等积法。●活动3 练兵之际用多媒体打出“总统证法”的图形问题:你能用此图形证明勾股定理吗?自己动手,拼出弦图让学生提前准备了四个全等的边长为a、b、c的直角三角形进行拼图。问题:你能用拼出的图形证明勾股定理吗?思想方法,这里具体地结合图形,利用勾股定理来证明.学生活动学生画图探究上台展示发现的结论,教师进行点评如果学生能答出正确答案,教师再追问:你是如何想到的?如果学生不能答出正确答案,教师再追问:这三个正方形的面积有怎样的等量关系?运用数学故事引入,激发学生的学习兴趣.研究问题的思路是从特殊到一般.教师引导学生从等腰直角三角形中发现三个正方形面积之间的等量关系,由面积之间的等量关系转化为三边的等量关系.地砖图案中的面积等量关系可以通过儿何直观得到,提高学生发现问题、提出问题的能力,学会用数学的眼光观察现实世界学生独立思考、作答,再全班交流教师引导学生类比上面等腰直角三角形的研究方法表示出所示的网格中直角三角形三边衍生的正方形的面积之间的关系 学生课前准备了“L”形,要求学生亲自动手,互相协助,将“L”形进行割补。学生回答:因为是割下来再补上去,所以前后面积相等。由此得到:a2+b2=c2独立思考举手回答:用“等积法”可证。类比等腰直角三角形的研究方法,从特殊到一般,借助网格,由直角三角形三边衍生的正方形面积关系表示三边之间的等量关系,体会研究问题的思路和方法,运用割补法求以直角三角形斜边为边长的正方形面积是本环节的难点,教师引导学生通过“割”形或者“补”形求正方形面积,培养学生的几何直观和运算能力;引导学生归纳并合理她用数学语言提出猜想,渗透转化思想,使学生学会用数学的语言表达现实世界.学生通过教师提出的问题串的引领,自主拼接、构造弦图,证明勾股定理,并且明晰每一个步骤的原理小组合作,进行拼图。上黑板将拼图粘贴在黑板上进行演示。学生通过以上步骤了解分割、拼接图形的目的和原理,从而进行自然、合理的再发现活动,通过对比拼接前后的图形,使学生能够从中理解变换前后图形的面积总和保持不变,体会“出入相补法”的原理.通过对“赵爽弦图”巧妙的证法介绍,弘扬我国古代的数学成就,培养学生的民族自豪感让学生感受数形结合这一数学思想,让学生亲自动手,互相协作,拿一块由a2和b2组成的不规则的平面图形经割补,变为规则的c2,又因两块割补前后面积相等,从而得到勾股定理:a2+b2= c2,也因此引入了“等积法”证明勾股定理。环节三:课堂总结1.勾股定理的内容是什么?它有什么作用? 2.在探究勾股定理的过程中,我们经历了怎样的探究过程?学到了用“等积法”证明勾股定理及数形结合的思想。感受到了数学的奇妙,也感受到了古人的伟大。我们一定要将此传承下去。设计意图:
板书设计《勾股定理》 a2+b2=c2
— 2 —
— 3 —
课题 《勾股定理》
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析勾股定理:直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.勾股定理是中学数学重要定理之一,它揭示了直角三角形三边之间的数量关系.由此,在直角三角形中已知任意两边长,就可以求出第三边长.勾股定理常用来求解线段长度或距离问题.勾股定理的探究是从特殊的等腰直角三角形出发,到网格中直角三角形,再到一般的直角三角形,体现了从特殊到一般的探究过程和研究方法.证明勾股定理的关键是利用割补法求以斜边为边长的正方形的面积,并以此引导学生发现证明勾股定理的思路.我国对勾股定理的研究和其他国家相比是比较早的,在国际上得到肯定.要通过我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感;要通过对勾股定理的探索和发现,培养学生学好数学的自信心. 基于以上分析,可以确定本节课的教学重点是:探索并证明勾股定理.
学情分析通过前面的学习,学生已经掌握了全等三角形、直角三角形两锐角互余、完全平方公式等基础知识,积累了通过测量、拼图、折纸来研究几何命题的基本活动经验,这些都为本节课探究和证明勾股定理奠定了基础.学生面对复杂图形的变换,对教材中给出的文字证明还存在一定的理解困难,提出问题的能力、逻辑推理能力还有待提高.
学习目标(1)经历勾股定理的探究过程.了解关于勾股定理的一些文化历史背景,通过对我国古代研究勾股定理的成就的介绍,培养学生的民族自豪感.(2)能用勾股定理解决一些简单问题.
重难点(1)会利用数形结合的思想说明勾股定理。(2)会利用勾股定理求直角三角形的边长。
教学评活动过程教师活动学生活动环节一:创设情境温故知新,情境创设引导语:前面我们已经研究了一般的三角形的边、角性质,本节课我们将研究特殊的三角形一一直角三角形.我们研究过直角三角形角的性质,那么直角三角形的三边之间具有怎样的等量关系呢?我们从特殊的直角三角形等腰直角三角形开始研究.学生聆听并思考从三角形的知识体系入手构建研究路径,体现知识之间的上下位关系,唤醒学生头脑中已有的相关知识,直接引入课题,使学生明确学习目标环节二:问题探究教师活动●活动1 观察、发现、类比、猜测1、通过多媒体让学生观察毕达哥拉斯家的磁砖 2、提问:是否任意直角三角形三边都符合等腰直角三角形三边的这个关系?引导学生由特殊到一般。3、由多媒体打出网格,在网格中给出任意三角形,引导学生到格点图中去验证自己的猜测。由于网格的不规则,引出用割补的方法进行计算。 ●活动2 实验探究,证明结论为了让学生感受数形结合这一数学思想,利用多媒体,要求学生由两块面积为a2与b2组成的图形经割补变为c2 提问:由以上过程,你能得到什么结论?由此我们得到了证明勾股定理的一种方法:等积法。●活动3 练兵之际用多媒体打出“总统证法”的图形问题:你能用此图形证明勾股定理吗?自己动手,拼出弦图让学生提前准备了四个全等的边长为a、b、c的直角三角形进行拼图。问题:你能用拼出的图形证明勾股定理吗?思想方法,这里具体地结合图形,利用勾股定理来证明.学生活动学生画图探究上台展示发现的结论,教师进行点评如果学生能答出正确答案,教师再追问:你是如何想到的?如果学生不能答出正确答案,教师再追问:这三个正方形的面积有怎样的等量关系?运用数学故事引入,激发学生的学习兴趣.研究问题的思路是从特殊到一般.教师引导学生从等腰直角三角形中发现三个正方形面积之间的等量关系,由面积之间的等量关系转化为三边的等量关系.地砖图案中的面积等量关系可以通过儿何直观得到,提高学生发现问题、提出问题的能力,学会用数学的眼光观察现实世界学生独立思考、作答,再全班交流教师引导学生类比上面等腰直角三角形的研究方法表示出所示的网格中直角三角形三边衍生的正方形的面积之间的关系 学生课前准备了“L”形,要求学生亲自动手,互相协助,将“L”形进行割补。学生回答:因为是割下来再补上去,所以前后面积相等。由此得到:a2+b2=c2独立思考举手回答:用“等积法”可证。类比等腰直角三角形的研究方法,从特殊到一般,借助网格,由直角三角形三边衍生的正方形面积关系表示三边之间的等量关系,体会研究问题的思路和方法,运用割补法求以直角三角形斜边为边长的正方形面积是本环节的难点,教师引导学生通过“割”形或者“补”形求正方形面积,培养学生的几何直观和运算能力;引导学生归纳并合理她用数学语言提出猜想,渗透转化思想,使学生学会用数学的语言表达现实世界.学生通过教师提出的问题串的引领,自主拼接、构造弦图,证明勾股定理,并且明晰每一个步骤的原理小组合作,进行拼图。上黑板将拼图粘贴在黑板上进行演示。学生通过以上步骤了解分割、拼接图形的目的和原理,从而进行自然、合理的再发现活动,通过对比拼接前后的图形,使学生能够从中理解变换前后图形的面积总和保持不变,体会“出入相补法”的原理.通过对“赵爽弦图”巧妙的证法介绍,弘扬我国古代的数学成就,培养学生的民族自豪感让学生感受数形结合这一数学思想,让学生亲自动手,互相协作,拿一块由a2和b2组成的不规则的平面图形经割补,变为规则的c2,又因两块割补前后面积相等,从而得到勾股定理:a2+b2= c2,也因此引入了“等积法”证明勾股定理。环节三:课堂总结1.勾股定理的内容是什么?它有什么作用? 2.在探究勾股定理的过程中,我们经历了怎样的探究过程?学到了用“等积法”证明勾股定理及数形结合的思想。感受到了数学的奇妙,也感受到了古人的伟大。我们一定要将此传承下去。设计意图:
板书设计《勾股定理》 a2+b2=c2
— 2 —
— 3 —
