6.6一次函数、一元一次方程和一元一次不等式同步练习(含解析) 苏科版数学八年级上册
文档属性
| 名称 | 6.6一次函数、一元一次方程和一元一次不等式同步练习(含解析) 苏科版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 06:35:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
6.6一次函数、一元一次方程和一元一次不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一次函数y1=kx+b与y2=mx+n的部分自变量和对应函数值如下表:
x … 0 1 2 3 …
y1 … 2 1 …
x … 0 1 2 3 …
y2 … ﹣3 ﹣1 1 3 …
则关于x的不等式kx+b>mx+n的解集是( )
A.x>2 B.x<2 C.x>1 D.x<1
2.如图,直线与的交点的横坐标为,则关于x的不等式的整数解可能是( )
A. B. C. D.1
3.如图,函数和的图象相交于点A,则不等式的解集为( )
A. B.
C. D.
4.如图,直线与直线交于点P(2,4),对关于的不等式的解集是( )
A. B. C. D.
5.若关于x的方程的解为,则直线一定经过点( )
A. B. C. D.
6.如图,直线与直线相交于点.根据图象可知,关于x的不等式的解集是( )
A. B. C. D.
7.若关于x的方程的解为,则直线一定经过点( )
A. B. C. D.
8.如图,在平面直角坐标系中,直线与直线相交于点,则关于x的不等式组的解集为( )
A. B. C. D.
9.一次函数的图象如图所示,当时,的取值范围( )
A. B. C. D.
10.如图,函数与的图象交于,则的解集为( )
A. B. C. D.
11.如图,一次函数与的图象交于点P.下列结论中,所有正确结论的个数是( )
①;②;③当时,;④;⑤.
A.1个 B.2个 C.3个 D.4个
12.如图,已知正比例函数和一次函数的图象相交于点,则根据图象可得不等式的解集是( )
A. B. C. D.
二、填空题
13.如图,一次函数的图象经过点A(1,2),关于x的不等式的解集为 .
14.若点P在函数的图象上,且到x轴的距离等于1,则点P的坐标是 .
15.已知直线与x轴和y轴的交点分别是和,那么关于x的不等式的解集是 .
16.如图,函数和的图相交于点,则不等式的解集为 .
17.一次函数与的图象如图所示,当时,,则满足条牛的k的取值范围是 .
三、解答题
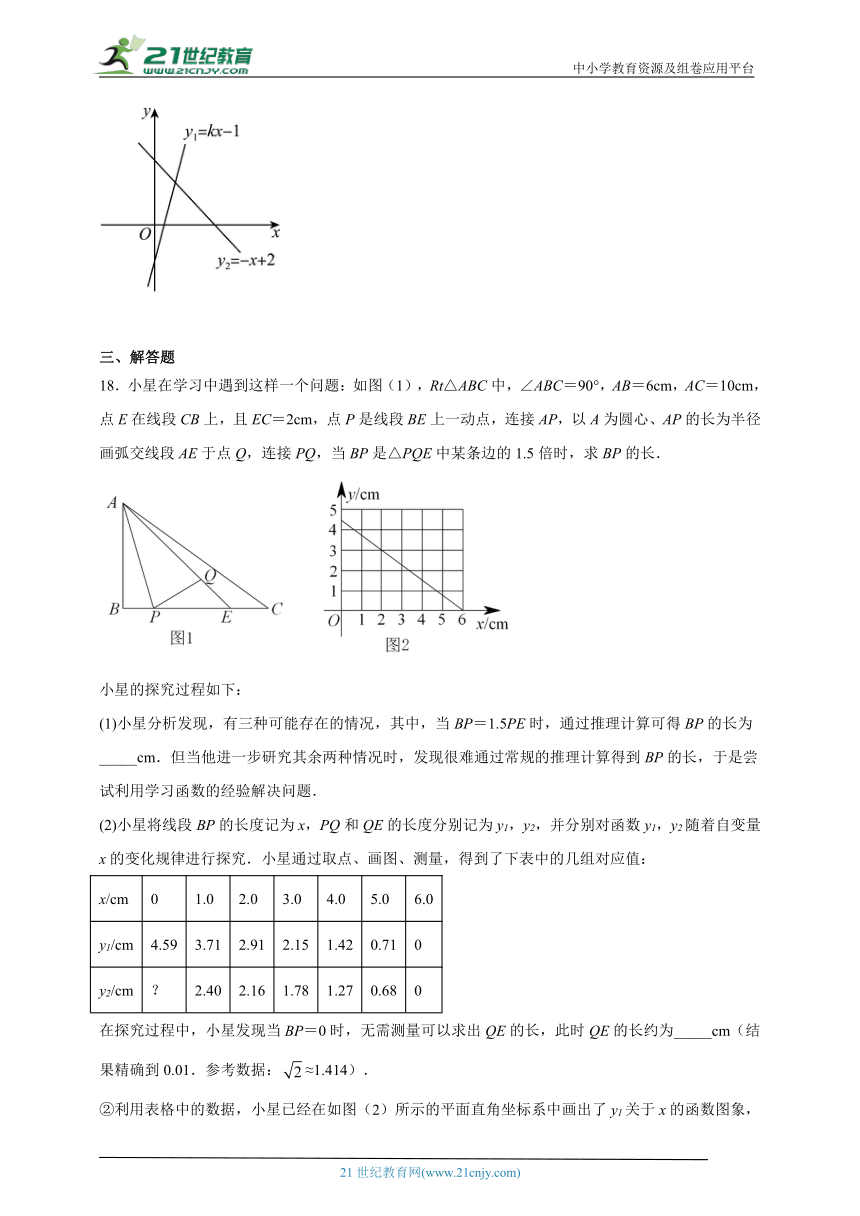
18.小星在学习中遇到这样一个问题:如图(1),Rt△ABC中,∠ABC=90°,AB=6cm,AC=10cm,点E在线段CB上,且EC=2cm,点P是线段BE上一动点,连接AP,以A为圆心、AP的长为半径画弧交线段AE于点Q,连接PQ,当BP是△PQE中某条边的1.5倍时,求BP的长.
小星的探究过程如下:
(1)小星分析发现,有三种可能存在的情况,其中,当BP=1.5PE时,通过推理计算可得BP的长为_____cm.但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到BP的长,于是尝试利用学习函数的经验解决问题.
(2)小星将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,并分别对函数y1,y2随着自变量x的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
x/cm 0 1.0 2.0 3.0 4.0 5.0 6.0
y1/cm 4.59 3.71 2.91 2.15 1.42 0.71 0
y2/cm ? 2.40 2.16 1.78 1.27 0.68 0
在探究过程中,小星发现当BP=0时,无需测量可以求出QE的长,此时QE的长约为_____cm(结果精确到0.01.参考数据:≈1.414).
②利用表格中的数据,小星已经在如图(2)所示的平面直角坐标系中画出了y1关于x的函数图象,请你根据上文中y2和x的7组对应值在此平面直角坐标系中描点,并画出y2关于x的函数图象
(3)小星发现,想用函数图象彻底解决这个问题,还需要在平面直角坐标系内再画出一个函数的图象,请直接写出这个函数的解析式:____,并在上述平面直角坐标系中画出该函数的图象.
(4)请结合图象直接写出:当BP是PQ或QE的1.5倍时,BP的长约为____(结果精确到0.1cm).
19.如图,正比例函数的图象经过点.
(1)求k的值;
(2)请在如图所示的平面直角坐标系中画出一次函数的图象;
(3)根据图象,直接写出关于x的不等式的取值范围是 .
20.如图,在矩形中,.动点P从点A出发,沿折线运动(运动路线不包含点A、点C),当它到点C时停止,设点P运动的路程为x,连接.设的面积为y.
(1)求出y与x的函数关系式,并注明x的取值范围,在x的取值范围内画出该函数图象;
(2)根据函数图象,写出该函数的一条性质;
(3)若直线与该函数图象有两个交点,直接写出k的取值范围.
21.已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式.
(2)当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
22.为进一步加强“书香校园”建设,某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高,用元购进的甲种书柜的数量比用元购进乙种书柜的数量少个.
(1)每个甲种书柜的进价是多少元?
(2)若该校拟购进这两种规格的书柜共个,其中乙种书柜的数量不大于甲种书柜数量的倍.该校应如何进货使得购进书柜所需费用最少?
23.已知:直线:().
(1)求证:直线恒过定点;
(2)已知点、坐标分别为,,若直线与线段相交,求的取值范围;
(3)在范围内,任取3个自变量,,,它们对应的函数值分别为,,,若以,,为长度的3条线段能围成三角形,直接写出的取值范围.
24.一次函数(k,b是常数,)和的图象交于点A.
(1)若点A在x轴上,求的值.
(2)若点,当时,,直接写出k的取值范围.
(3)若,点在一次函数图象上,求证:.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C A A A D D B
题号 11 12
答案 C C
1.B
【分析】根据表格数据可得两个函数图像的交点坐标是(2,1),结合函数的增减性,即可求解.
【详解】解:根据表可得 中y随x的增大而减小;
中y随x的增大而增大.且两个函数图像的交点坐标是(2,1).
则当 时,
故选B.
【点睛】本题主要考查一次函数图像和不等式的解,从表格中得出两个函数图像的交点坐标是(2,1)是关键.
2.A
【分析】满足关于x的不等式nx+4n> x+m>0就是在x轴的上方且直线y=nx+4n位于直线y= x+m的上方的图象,据此求得自变量的取值范围,进而求解即可.
【详解】解:∵直线y= x+m与y=nx+4n的交点的横坐标为 2,
∴关于x的不等式nx+4n> x+m的解集为x> 2,
∵ x+m>0
∴由图象可知,x<m
又∵ 2<m<0,
∴ 2<x<0,
∴整数解可能是 1.
故选:A.
【点睛】本题考查了一次函数的图象和性质以及与一元一次不等式的关系,要熟练掌握.
3.B
【分析】利用函数图象,找出直线y=bx不在直线y=ax+4的下方所对应的自变量的范围即可.
【详解】解:根据函数图象,当x≥2时,ax+4≤bx.
故选:B.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
4.C
【分析】根据函数图象,可以发现当x>2时,一次函数y=x+b的图象在y=kx+5的图象的上方,从而可以得到不等式x+b>kx+5的解集.
【详解】解:由图象可得,
当x>2时,一次函数y=x+b的图象在y=kx+5的图象的上方,
∴不等式x+b>kx+5的解集是x>2,
故选:C.
【点睛】本题考查一次函数与一元一次不等式、一次函数的图象,利用数形结合的思想解答问题是解答本题的关键.
5.A
【分析】本题主要考查了一元一次方程解的定义,一次函数的性质,先把代入方程中得到,进而得到当时,,据此可得答案.
【详解】解:∵关于x的方程的解是,
∴,
∴,
∴直线解析式为,
∴当时,,即直线一定经过点,
故选:A.
6.A
【分析】本题考查一次函数与一元一次不等式,利用图象法求不等式的解集即可.
【详解】解:由图象可知:当时,直线在直线的上方,
∴的解集为:;
故选A.
7.A
【分析】根据方程可知当x=2,y=0,从而可判断直线y=-2x+b经过点(2,0).
【详解】解:由方程的解可知:当x=2时,-2x+b=0,即当x=2,y=0,
∴直线y=-2x+b的图象一定经过点(2,0),
故选:A.
【点睛】本题主要考查的是一次函数与一元一次方程的关系,掌握一次函数与一元一次方程的关系是解题的关键.
8.D
【分析】本题考查了一次函数与一元一次不等式的关系,观察分析函数图象是解题的关键.
首先求出,,得到当时,,观察函数图象得到,当时,的图象都在的图象的上方,且,由此即可得到不等式组的解集.
【详解】解:将代入得,
解得
∴
∴将代入得,
解得
∴
∴当时,,
当时,的图象都在的图象的上方,且
∴关于x的不等式组的解集为.
故选:D.
9.D
【分析】本题考查一次函数与一元一次不等式,观察图象知,直线与x轴交于.在交点左边,图象在x轴上方,即当时,.
【详解】观察图象知,当时,.
故选:D.
10.B
【分析】先把P(n,-2)代入y=-2x+3求出n得到P的坐标,根据图象直接写出直线y=- x+m在直线y=-2x+3的上方所对应的自变量的范围即可.
【详解】解:把P(n,-2)代入y=-2x+3得-2n+3=-2,解得n=;
∴P(,-2),
观察图象,当x>时,直线y=- x+m在直线y=-2x+3的上方,
∴不等式-x+m>-2x+3的解集为x>.
故选:B.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
11.C
【分析】仔细观察图象:①根据一次函数y=ax+b图象从左向右变化趋势及与y轴交点即可判断a、b的正负;②根据一次函数y=cx+d图象从左向右变化趋势及与y轴交点可判断c、d的正负,即可得出结论;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④由两个一次函数图象的交点坐标的横坐标为1可得出结论;⑤由一次函数y=cx+d图象与x轴的交点坐标为(,0),可得>-1,解此不等式即可作出判断.
【详解】解:①由图象可得:一次函数y=ax+b图象经过一、二、四象限,
∴a<0,b>0,故①错误;
②由图象可得:一次函数y=cx+d图象经过一、二、三象限,
∴c>0,d>0,
∴ac<0,故②正确;
③由图象可得:当x>1时,一次函数y=ax+b图象在y=cx+d的图象下方,
∴ax+b<cx+d,故③错误;
④∵一次函数y=ax+b与y=cx+d的图象的交点P的横坐标为1,
∴a+b=c+d,故④正确;
⑤∵一次函数y=cx+d图象与x轴的交点坐标为(,0),且>-1,
∵c>0,
∴-d>-c,
∴c>d.故⑤正确.
正确的有②④⑤,
故选:C.
【点睛】本题考查了一次函数的图象与性质、一次函数与一元一次不等式,掌握一次函数的图象与性质并利用数形结合的思想是解题的关键.
12.C
【分析】观察图象得:当时,正比例函数的图象位于一次函数的图象上方,即可求解.
【详解】解:观察图象得:当时,正比例函数的图象位于一次函数的图象上方,
∴不等式的解集是.
故选:C
【点睛】本题主要考查了一次函数与不等式的关系,利用数形结合思想解答是解题的关键.
13.x>1
【分析】观察函数图象得到即可.
【详解】解:由图象可得:当x>1时,kx+b>2,
所以关于x的不等式kx+b>2的解集是x>1,
故答案为x>1.
【点睛】本题考查了一次函数与一元一次不等式的关系,理解题意,利用数形结合思想求解是解题关键.
14.(-1,1)或(1,1)
【分析】根据点P到x轴的距离等于1可得y=1或y=-1,根据点P在函数的图象上,可得当y=1时,x=1或-1,当y=-1时,x无解,从而得出答案.
【详解】解:∵点P到x轴的距离等于1,
∴点P的纵坐标为1或-1,
即y=1或y=-1,
∵点P在函数的图象上,
当y=1时,x=1或-1,
∴点P(-1,1)或(1,1),
当y=-1时,x无解,
综上所述,点P的坐标是(-1,1)或(1,1).
故答案为(-1,1)或(1,1).
【点睛】本题考查了一次函数图象上点的坐标特征及解一元一次方程.点到x轴的距离等于该点的纵坐标的绝对值;点在函数解析式上,点的横纵坐标适合这个函数解析式.
15.
【分析】由题意可以求得k和b的值,代入不等式即可得到正确答案 .
【详解】解:由题意可得:,
,
∴原不等式即为,
解得:,
故答案为:.
【点睛】本题考查一次函数与一元一次不等式的综合应用,利用直线与坐标轴的交点求出不等式的系数是解题关键.
16./
【分析】本题考查一次函数与一元一次不等式,图象法解不等式即可.
【详解】解:由图象可知:的解集为:.
故答案为:.
17.且
【分析】本题考查根据两条直线的交点求不等式的解集,联立与,求出两条直线交点的横坐标,根据当时,,结合图象列不等式,即可求解.
【详解】解:联立与,
得,
解得,
即一次函数()与的图像的交点的横坐标为,
当时,,
,
∴,
解得;
当时,与两条直线平行,且的图象在直线的下方,所以,当时,,满足题意;
又,
满足条件的的取值范围是且,
故答案为:且.
18.(1)3.6;
(2)①2.48;②见解析;
(3),函数图象见解析;
(4)2.8cm或3.1cm.
【分析】(1)先通过勾股定理求出BC的长度,根据EC=2cm,即可求出BE的长度,最后通过BP=1.5PE即可求出BP的长度;
(2)①根据题意可知AP=AQ,当BP=0时则点P与点B重合,此时勾股定理求出AE的长度,用AE-AQ即可求出QE的长度;②根据表格中的数据描点画图即可;
(3)根据BP是△PQE中某条边的1.5倍,可得到BP=1.5PQ或BP=1.5QE,即PQ=BP或QE=BP;将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,直接写出y与x的函数表达式再画出该函数的图象即可;
(4)结合图象,分别找出与(2)中的两个函数图象的交点,找出交点的横坐标即可.
【详解】(1)在Rt△ABC中,由勾股定理可得:BC=(cm)
∵EC=2cm,
∴BE=BC-EC=8-2=6(cm),
∵BP=1.5PE,
∴设PE=m,则BP=1.5m,
列出方程得:m+1.5m=6,解得:m=2.4,
∴BP=1.5m=1.5×2.4=3.6(cm),
故答案为:3.6;
(2)①∵以A为圆心、AP的长为半径画弧交线段AE于点Q,
∴AP=AQ,
当BP=0时,点P与点B重合,此时AP=AB=6cm,
∴AQ=6cm,
由(1)可得:BE=6cm,
在Rt△ABE中,由勾股定理可得:AE=(cm),
∴QE=AE-AQ=≈2.48(cm),
故答案为:2.48;
②如图:
(3)∵BP是△PQE中某条边的1.5倍,
∴BP=1.5PQ或BP=1.5QE,即PQ=BP或QE=BP;
将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,
∴,,
故还需要画出的函数图象,
如图:
(4)由图可知,与两函数的交点分别为点M和点N,
∵点M的横坐标约为2.8;点N的横坐标约为3.1;
∴当BP是PQ或QE的1.5倍时,BP的长约为2.8cm或3.1cm,
故答案为:2.8cm或3.1cm
【点睛】本题主要考查了函数图象的画法,函数图象交点的意义以及勾股定理,仔细体会题意运用数形结合的思想来解决问题是解题的关键.
19.(1)
(2)见解析
(3)
【分析】(1)把点代入可得的值;
(2)根据一次函数经过的点和,然后画出图象即可;
(3)结合图象,直接求解即可.
【详解】(1)解:∵正比例函数的图象经过点,
∴,解得.
(2)根据一次函数经过的点和,过这两点画一条直线,如图所示,
直线即为所画.
(3)由图象得:的解为,
故答案为:.
【点睛】此题主要考查了一次函数的性质,以及函数图象上点的坐标特点,待定系数法求一次函数解析式,关键是掌握一次函数图象上点的坐标特征.
20.(1),见解析
(2)见解析,(合理即可)
(3)
【分析】(1)由题意知,当时,,则;当时,,则;然后作图象即可;
(2)根据图象作答即可;
(3)当时,,即为过的直线,如图3,将代入,可求;将代入,可求;结合图象进而可得取值范围.
【详解】(1)解:由题意知,当时,,
∴;
当时,,
∴;
∴;
作图如图2;
(2)解:由图象可知,当时,随着的增大而增大,当时,随着的增大而减小;
(3)解:当时,,
∴为过的直线,
如图3,
将代入得,,
解得,;
将代入得,,
解得,;
由图象可知,当时,直线与该函数图象有两个交点.
【点睛】本题考查了一次函数的应用,一次函数解析式,一次函数的图象与性质,两直线交点.熟练掌握一次函数的图象与性质并数形结合是解题的关键.
21.(1)
(2)生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元
【分析】本题考查了一次函数的应用,解题时首先正确理解题意,然后利用题目的数量关系列出函数解析式.
(1)由于计划用这两种布料生产M、N两种型号的时装共80套,生产M型号的时装套数为x,做一套M型号的时装可获利100元,做一套N型号的时装可获利45元,由此即可求解.
(2)首先利用不等式组得出x的取值范围,再根据一次函数的性质可得最大利润.
【详解】(1)
故答案为:;
(2)两种型号的时装共用布料米米,
解得,
随x的增大而增大,
当时,,
即生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元.
22.(1)每个甲种书柜的进价为元
(2)购进甲书柜个,购进乙书柜个,费用最少
【分析】本题考查分式方程,一元一次不等式,一次函数的知识,解题的关键是掌握分式方程,一元一次不等式的运用,一次函数的运用,即可.
(1)设每个乙种书柜的进价为元,每个甲种书柜的进价为元,根据题意,列出分式方程,即可;
(2)设甲书柜的数量为个,则乙书柜的数量为个,求出的范围,设使得购进书柜所需费用为,根据题意,求出函数关系,根据函数的性质,即可.
【详解】(1)设每个乙种书柜的进价为元,每个甲种书柜的进价为元,
∴,
解得:,
经检验,是方程的解,
∴,
答:每个甲种书柜的进价为元.
(2)设甲书柜的数量为个,
∴乙书柜的数量为个,
∵乙种书柜的数量不大于甲种书柜数量的倍,
∴,
解得:,
∴,
设使得购进书柜所需费用为,
∴,
整理得:,
当时,有最小值,,
答:购进甲书柜个,购进乙书柜个,费用最少.
23.(1)
(2)
(3)或
【分析】(1)将整理成,进而求解即可;
(2)根据点A、坐标分别为,,直线与线段相交,直线l:,恒过某一定点得当时,,当时,,即可得,进行计算即可得;
(3)当时,直线l:中,随的增大而增大,可得当时,, 根据以、、为长度的条线段能围成三角形得,解得,即可得,当时,直线中,随的增大而减小,当时,,根据以、、为长度的条线段能围成三角形得,解得,则,即可得.
【详解】(1)证明:,
当时,,
直线恒过定点;
(2)解:∵点A、坐标分别为,,直线与线段相交,直线l:,恒过某一定点,
当时,,当时,,
∴,
解得;
(3)解:当时,直线l:中,随的增大而增大,
当时,,
∵以、、为长度的条线段能围成三角形,
∴,
解得,
∴,
当时,直线中,随的增大而减小,
当时,,
∵以、、为长度的条线段能围成三角形,
∴,
解得,
∴,
由上可得,或.
【点睛】本题考查了一次函数图象与性质,一次函数图象上点的坐标特征,三角形三边关系,解题的关键是理解题意,掌握这些知识点.
24.(1)2
(2)
(3)见解析.
【分析】(1)点A在x轴上,可以设代入,求得a的值,再将代入整理即可得到的值;
(2)将代入求得m的值,再将代入可得,由解不等式,结合解集为,即可求得k的范围;
(3)将代入,求得,再代入,即可求证.
【详解】(1)在x轴上,
设,代入,解得,
将代入,得:,
整理,得:.
(2)将代入,得:,
将代入,得:,
当时, ,
关于x的不等式的解集为,
即:的解集为,
由不等式的性质可知:,
解得:.
(3)将代入,得:,
,解得:
,
.
【点睛】本题主要考查一次函数背景下一次方程与不等式的求解问题,准确理解题意构造相应的不等式是本题的解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.6一次函数、一元一次方程和一元一次不等式
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一次函数y1=kx+b与y2=mx+n的部分自变量和对应函数值如下表:
x … 0 1 2 3 …
y1 … 2 1 …
x … 0 1 2 3 …
y2 … ﹣3 ﹣1 1 3 …
则关于x的不等式kx+b>mx+n的解集是( )
A.x>2 B.x<2 C.x>1 D.x<1
2.如图,直线与的交点的横坐标为,则关于x的不等式的整数解可能是( )
A. B. C. D.1
3.如图,函数和的图象相交于点A,则不等式的解集为( )
A. B.
C. D.
4.如图,直线与直线交于点P(2,4),对关于的不等式的解集是( )
A. B. C. D.
5.若关于x的方程的解为,则直线一定经过点( )
A. B. C. D.
6.如图,直线与直线相交于点.根据图象可知,关于x的不等式的解集是( )
A. B. C. D.
7.若关于x的方程的解为,则直线一定经过点( )
A. B. C. D.
8.如图,在平面直角坐标系中,直线与直线相交于点,则关于x的不等式组的解集为( )
A. B. C. D.
9.一次函数的图象如图所示,当时,的取值范围( )
A. B. C. D.
10.如图,函数与的图象交于,则的解集为( )
A. B. C. D.
11.如图,一次函数与的图象交于点P.下列结论中,所有正确结论的个数是( )
①;②;③当时,;④;⑤.
A.1个 B.2个 C.3个 D.4个
12.如图,已知正比例函数和一次函数的图象相交于点,则根据图象可得不等式的解集是( )
A. B. C. D.
二、填空题
13.如图,一次函数的图象经过点A(1,2),关于x的不等式的解集为 .
14.若点P在函数的图象上,且到x轴的距离等于1,则点P的坐标是 .
15.已知直线与x轴和y轴的交点分别是和,那么关于x的不等式的解集是 .
16.如图,函数和的图相交于点,则不等式的解集为 .
17.一次函数与的图象如图所示,当时,,则满足条牛的k的取值范围是 .
三、解答题
18.小星在学习中遇到这样一个问题:如图(1),Rt△ABC中,∠ABC=90°,AB=6cm,AC=10cm,点E在线段CB上,且EC=2cm,点P是线段BE上一动点,连接AP,以A为圆心、AP的长为半径画弧交线段AE于点Q,连接PQ,当BP是△PQE中某条边的1.5倍时,求BP的长.
小星的探究过程如下:
(1)小星分析发现,有三种可能存在的情况,其中,当BP=1.5PE时,通过推理计算可得BP的长为_____cm.但当他进一步研究其余两种情况时,发现很难通过常规的推理计算得到BP的长,于是尝试利用学习函数的经验解决问题.
(2)小星将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,并分别对函数y1,y2随着自变量x的变化规律进行探究.小星通过取点、画图、测量,得到了下表中的几组对应值:
x/cm 0 1.0 2.0 3.0 4.0 5.0 6.0
y1/cm 4.59 3.71 2.91 2.15 1.42 0.71 0
y2/cm ? 2.40 2.16 1.78 1.27 0.68 0
在探究过程中,小星发现当BP=0时,无需测量可以求出QE的长,此时QE的长约为_____cm(结果精确到0.01.参考数据:≈1.414).
②利用表格中的数据,小星已经在如图(2)所示的平面直角坐标系中画出了y1关于x的函数图象,请你根据上文中y2和x的7组对应值在此平面直角坐标系中描点,并画出y2关于x的函数图象
(3)小星发现,想用函数图象彻底解决这个问题,还需要在平面直角坐标系内再画出一个函数的图象,请直接写出这个函数的解析式:____,并在上述平面直角坐标系中画出该函数的图象.
(4)请结合图象直接写出:当BP是PQ或QE的1.5倍时,BP的长约为____(结果精确到0.1cm).
19.如图,正比例函数的图象经过点.
(1)求k的值;
(2)请在如图所示的平面直角坐标系中画出一次函数的图象;
(3)根据图象,直接写出关于x的不等式的取值范围是 .
20.如图,在矩形中,.动点P从点A出发,沿折线运动(运动路线不包含点A、点C),当它到点C时停止,设点P运动的路程为x,连接.设的面积为y.
(1)求出y与x的函数关系式,并注明x的取值范围,在x的取值范围内画出该函数图象;
(2)根据函数图象,写出该函数的一条性质;
(3)若直线与该函数图象有两个交点,直接写出k的取值范围.
21.已知某服装厂现有布料70米,现计划用这种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用布料1.6米,可获利100元;做一套N型号的时装需用布料0.6米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式.
(2)当生产M型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
22.为进一步加强“书香校园”建设,某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高,用元购进的甲种书柜的数量比用元购进乙种书柜的数量少个.
(1)每个甲种书柜的进价是多少元?
(2)若该校拟购进这两种规格的书柜共个,其中乙种书柜的数量不大于甲种书柜数量的倍.该校应如何进货使得购进书柜所需费用最少?
23.已知:直线:().
(1)求证:直线恒过定点;
(2)已知点、坐标分别为,,若直线与线段相交,求的取值范围;
(3)在范围内,任取3个自变量,,,它们对应的函数值分别为,,,若以,,为长度的3条线段能围成三角形,直接写出的取值范围.
24.一次函数(k,b是常数,)和的图象交于点A.
(1)若点A在x轴上,求的值.
(2)若点,当时,,直接写出k的取值范围.
(3)若,点在一次函数图象上,求证:.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C A A A D D B
题号 11 12
答案 C C
1.B
【分析】根据表格数据可得两个函数图像的交点坐标是(2,1),结合函数的增减性,即可求解.
【详解】解:根据表可得 中y随x的增大而减小;
中y随x的增大而增大.且两个函数图像的交点坐标是(2,1).
则当 时,
故选B.
【点睛】本题主要考查一次函数图像和不等式的解,从表格中得出两个函数图像的交点坐标是(2,1)是关键.
2.A
【分析】满足关于x的不等式nx+4n> x+m>0就是在x轴的上方且直线y=nx+4n位于直线y= x+m的上方的图象,据此求得自变量的取值范围,进而求解即可.
【详解】解:∵直线y= x+m与y=nx+4n的交点的横坐标为 2,
∴关于x的不等式nx+4n> x+m的解集为x> 2,
∵ x+m>0
∴由图象可知,x<m
又∵ 2<m<0,
∴ 2<x<0,
∴整数解可能是 1.
故选:A.
【点睛】本题考查了一次函数的图象和性质以及与一元一次不等式的关系,要熟练掌握.
3.B
【分析】利用函数图象,找出直线y=bx不在直线y=ax+4的下方所对应的自变量的范围即可.
【详解】解:根据函数图象,当x≥2时,ax+4≤bx.
故选:B.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
4.C
【分析】根据函数图象,可以发现当x>2时,一次函数y=x+b的图象在y=kx+5的图象的上方,从而可以得到不等式x+b>kx+5的解集.
【详解】解:由图象可得,
当x>2时,一次函数y=x+b的图象在y=kx+5的图象的上方,
∴不等式x+b>kx+5的解集是x>2,
故选:C.
【点睛】本题考查一次函数与一元一次不等式、一次函数的图象,利用数形结合的思想解答问题是解答本题的关键.
5.A
【分析】本题主要考查了一元一次方程解的定义,一次函数的性质,先把代入方程中得到,进而得到当时,,据此可得答案.
【详解】解:∵关于x的方程的解是,
∴,
∴,
∴直线解析式为,
∴当时,,即直线一定经过点,
故选:A.
6.A
【分析】本题考查一次函数与一元一次不等式,利用图象法求不等式的解集即可.
【详解】解:由图象可知:当时,直线在直线的上方,
∴的解集为:;
故选A.
7.A
【分析】根据方程可知当x=2,y=0,从而可判断直线y=-2x+b经过点(2,0).
【详解】解:由方程的解可知:当x=2时,-2x+b=0,即当x=2,y=0,
∴直线y=-2x+b的图象一定经过点(2,0),
故选:A.
【点睛】本题主要考查的是一次函数与一元一次方程的关系,掌握一次函数与一元一次方程的关系是解题的关键.
8.D
【分析】本题考查了一次函数与一元一次不等式的关系,观察分析函数图象是解题的关键.
首先求出,,得到当时,,观察函数图象得到,当时,的图象都在的图象的上方,且,由此即可得到不等式组的解集.
【详解】解:将代入得,
解得
∴
∴将代入得,
解得
∴
∴当时,,
当时,的图象都在的图象的上方,且
∴关于x的不等式组的解集为.
故选:D.
9.D
【分析】本题考查一次函数与一元一次不等式,观察图象知,直线与x轴交于.在交点左边,图象在x轴上方,即当时,.
【详解】观察图象知,当时,.
故选:D.
10.B
【分析】先把P(n,-2)代入y=-2x+3求出n得到P的坐标,根据图象直接写出直线y=- x+m在直线y=-2x+3的上方所对应的自变量的范围即可.
【详解】解:把P(n,-2)代入y=-2x+3得-2n+3=-2,解得n=;
∴P(,-2),
观察图象,当x>时,直线y=- x+m在直线y=-2x+3的上方,
∴不等式-x+m>-2x+3的解集为x>.
故选:B.
【点睛】本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
11.C
【分析】仔细观察图象:①根据一次函数y=ax+b图象从左向右变化趋势及与y轴交点即可判断a、b的正负;②根据一次函数y=cx+d图象从左向右变化趋势及与y轴交点可判断c、d的正负,即可得出结论;③以两条直线的交点为分界,哪个函数图象在上面,则哪个函数值大;④由两个一次函数图象的交点坐标的横坐标为1可得出结论;⑤由一次函数y=cx+d图象与x轴的交点坐标为(,0),可得>-1,解此不等式即可作出判断.
【详解】解:①由图象可得:一次函数y=ax+b图象经过一、二、四象限,
∴a<0,b>0,故①错误;
②由图象可得:一次函数y=cx+d图象经过一、二、三象限,
∴c>0,d>0,
∴ac<0,故②正确;
③由图象可得:当x>1时,一次函数y=ax+b图象在y=cx+d的图象下方,
∴ax+b<cx+d,故③错误;
④∵一次函数y=ax+b与y=cx+d的图象的交点P的横坐标为1,
∴a+b=c+d,故④正确;
⑤∵一次函数y=cx+d图象与x轴的交点坐标为(,0),且>-1,
∵c>0,
∴-d>-c,
∴c>d.故⑤正确.
正确的有②④⑤,
故选:C.
【点睛】本题考查了一次函数的图象与性质、一次函数与一元一次不等式,掌握一次函数的图象与性质并利用数形结合的思想是解题的关键.
12.C
【分析】观察图象得:当时,正比例函数的图象位于一次函数的图象上方,即可求解.
【详解】解:观察图象得:当时,正比例函数的图象位于一次函数的图象上方,
∴不等式的解集是.
故选:C
【点睛】本题主要考查了一次函数与不等式的关系,利用数形结合思想解答是解题的关键.
13.x>1
【分析】观察函数图象得到即可.
【详解】解:由图象可得:当x>1时,kx+b>2,
所以关于x的不等式kx+b>2的解集是x>1,
故答案为x>1.
【点睛】本题考查了一次函数与一元一次不等式的关系,理解题意,利用数形结合思想求解是解题关键.
14.(-1,1)或(1,1)
【分析】根据点P到x轴的距离等于1可得y=1或y=-1,根据点P在函数的图象上,可得当y=1时,x=1或-1,当y=-1时,x无解,从而得出答案.
【详解】解:∵点P到x轴的距离等于1,
∴点P的纵坐标为1或-1,
即y=1或y=-1,
∵点P在函数的图象上,
当y=1时,x=1或-1,
∴点P(-1,1)或(1,1),
当y=-1时,x无解,
综上所述,点P的坐标是(-1,1)或(1,1).
故答案为(-1,1)或(1,1).
【点睛】本题考查了一次函数图象上点的坐标特征及解一元一次方程.点到x轴的距离等于该点的纵坐标的绝对值;点在函数解析式上,点的横纵坐标适合这个函数解析式.
15.
【分析】由题意可以求得k和b的值,代入不等式即可得到正确答案 .
【详解】解:由题意可得:,
,
∴原不等式即为,
解得:,
故答案为:.
【点睛】本题考查一次函数与一元一次不等式的综合应用,利用直线与坐标轴的交点求出不等式的系数是解题关键.
16./
【分析】本题考查一次函数与一元一次不等式,图象法解不等式即可.
【详解】解:由图象可知:的解集为:.
故答案为:.
17.且
【分析】本题考查根据两条直线的交点求不等式的解集,联立与,求出两条直线交点的横坐标,根据当时,,结合图象列不等式,即可求解.
【详解】解:联立与,
得,
解得,
即一次函数()与的图像的交点的横坐标为,
当时,,
,
∴,
解得;
当时,与两条直线平行,且的图象在直线的下方,所以,当时,,满足题意;
又,
满足条件的的取值范围是且,
故答案为:且.
18.(1)3.6;
(2)①2.48;②见解析;
(3),函数图象见解析;
(4)2.8cm或3.1cm.
【分析】(1)先通过勾股定理求出BC的长度,根据EC=2cm,即可求出BE的长度,最后通过BP=1.5PE即可求出BP的长度;
(2)①根据题意可知AP=AQ,当BP=0时则点P与点B重合,此时勾股定理求出AE的长度,用AE-AQ即可求出QE的长度;②根据表格中的数据描点画图即可;
(3)根据BP是△PQE中某条边的1.5倍,可得到BP=1.5PQ或BP=1.5QE,即PQ=BP或QE=BP;将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,直接写出y与x的函数表达式再画出该函数的图象即可;
(4)结合图象,分别找出与(2)中的两个函数图象的交点,找出交点的横坐标即可.
【详解】(1)在Rt△ABC中,由勾股定理可得:BC=(cm)
∵EC=2cm,
∴BE=BC-EC=8-2=6(cm),
∵BP=1.5PE,
∴设PE=m,则BP=1.5m,
列出方程得:m+1.5m=6,解得:m=2.4,
∴BP=1.5m=1.5×2.4=3.6(cm),
故答案为:3.6;
(2)①∵以A为圆心、AP的长为半径画弧交线段AE于点Q,
∴AP=AQ,
当BP=0时,点P与点B重合,此时AP=AB=6cm,
∴AQ=6cm,
由(1)可得:BE=6cm,
在Rt△ABE中,由勾股定理可得:AE=(cm),
∴QE=AE-AQ=≈2.48(cm),
故答案为:2.48;
②如图:
(3)∵BP是△PQE中某条边的1.5倍,
∴BP=1.5PQ或BP=1.5QE,即PQ=BP或QE=BP;
将线段BP的长度记为x,PQ和QE的长度分别记为y1,y2,
∴,,
故还需要画出的函数图象,
如图:
(4)由图可知,与两函数的交点分别为点M和点N,
∵点M的横坐标约为2.8;点N的横坐标约为3.1;
∴当BP是PQ或QE的1.5倍时,BP的长约为2.8cm或3.1cm,
故答案为:2.8cm或3.1cm
【点睛】本题主要考查了函数图象的画法,函数图象交点的意义以及勾股定理,仔细体会题意运用数形结合的思想来解决问题是解题的关键.
19.(1)
(2)见解析
(3)
【分析】(1)把点代入可得的值;
(2)根据一次函数经过的点和,然后画出图象即可;
(3)结合图象,直接求解即可.
【详解】(1)解:∵正比例函数的图象经过点,
∴,解得.
(2)根据一次函数经过的点和,过这两点画一条直线,如图所示,
直线即为所画.
(3)由图象得:的解为,
故答案为:.
【点睛】此题主要考查了一次函数的性质,以及函数图象上点的坐标特点,待定系数法求一次函数解析式,关键是掌握一次函数图象上点的坐标特征.
20.(1),见解析
(2)见解析,(合理即可)
(3)
【分析】(1)由题意知,当时,,则;当时,,则;然后作图象即可;
(2)根据图象作答即可;
(3)当时,,即为过的直线,如图3,将代入,可求;将代入,可求;结合图象进而可得取值范围.
【详解】(1)解:由题意知,当时,,
∴;
当时,,
∴;
∴;
作图如图2;
(2)解:由图象可知,当时,随着的增大而增大,当时,随着的增大而减小;
(3)解:当时,,
∴为过的直线,
如图3,
将代入得,,
解得,;
将代入得,,
解得,;
由图象可知,当时,直线与该函数图象有两个交点.
【点睛】本题考查了一次函数的应用,一次函数解析式,一次函数的图象与性质,两直线交点.熟练掌握一次函数的图象与性质并数形结合是解题的关键.
21.(1)
(2)生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元
【分析】本题考查了一次函数的应用,解题时首先正确理解题意,然后利用题目的数量关系列出函数解析式.
(1)由于计划用这两种布料生产M、N两种型号的时装共80套,生产M型号的时装套数为x,做一套M型号的时装可获利100元,做一套N型号的时装可获利45元,由此即可求解.
(2)首先利用不等式组得出x的取值范围,再根据一次函数的性质可得最大利润.
【详解】(1)
故答案为:;
(2)两种型号的时装共用布料米米,
解得,
随x的增大而增大,
当时,,
即生产M型号的时装22套时,该厂所获利润最大,最大利润是4810元.
22.(1)每个甲种书柜的进价为元
(2)购进甲书柜个,购进乙书柜个,费用最少
【分析】本题考查分式方程,一元一次不等式,一次函数的知识,解题的关键是掌握分式方程,一元一次不等式的运用,一次函数的运用,即可.
(1)设每个乙种书柜的进价为元,每个甲种书柜的进价为元,根据题意,列出分式方程,即可;
(2)设甲书柜的数量为个,则乙书柜的数量为个,求出的范围,设使得购进书柜所需费用为,根据题意,求出函数关系,根据函数的性质,即可.
【详解】(1)设每个乙种书柜的进价为元,每个甲种书柜的进价为元,
∴,
解得:,
经检验,是方程的解,
∴,
答:每个甲种书柜的进价为元.
(2)设甲书柜的数量为个,
∴乙书柜的数量为个,
∵乙种书柜的数量不大于甲种书柜数量的倍,
∴,
解得:,
∴,
设使得购进书柜所需费用为,
∴,
整理得:,
当时,有最小值,,
答:购进甲书柜个,购进乙书柜个,费用最少.
23.(1)
(2)
(3)或
【分析】(1)将整理成,进而求解即可;
(2)根据点A、坐标分别为,,直线与线段相交,直线l:,恒过某一定点得当时,,当时,,即可得,进行计算即可得;
(3)当时,直线l:中,随的增大而增大,可得当时,, 根据以、、为长度的条线段能围成三角形得,解得,即可得,当时,直线中,随的增大而减小,当时,,根据以、、为长度的条线段能围成三角形得,解得,则,即可得.
【详解】(1)证明:,
当时,,
直线恒过定点;
(2)解:∵点A、坐标分别为,,直线与线段相交,直线l:,恒过某一定点,
当时,,当时,,
∴,
解得;
(3)解:当时,直线l:中,随的增大而增大,
当时,,
∵以、、为长度的条线段能围成三角形,
∴,
解得,
∴,
当时,直线中,随的增大而减小,
当时,,
∵以、、为长度的条线段能围成三角形,
∴,
解得,
∴,
由上可得,或.
【点睛】本题考查了一次函数图象与性质,一次函数图象上点的坐标特征,三角形三边关系,解题的关键是理解题意,掌握这些知识点.
24.(1)2
(2)
(3)见解析.
【分析】(1)点A在x轴上,可以设代入,求得a的值,再将代入整理即可得到的值;
(2)将代入求得m的值,再将代入可得,由解不等式,结合解集为,即可求得k的范围;
(3)将代入,求得,再代入,即可求证.
【详解】(1)在x轴上,
设,代入,解得,
将代入,得:,
整理,得:.
(2)将代入,得:,
将代入,得:,
当时, ,
关于x的不等式的解集为,
即:的解集为,
由不等式的性质可知:,
解得:.
(3)将代入,得:,
,解得:
,
.
【点睛】本题主要考查一次函数背景下一次方程与不等式的求解问题,准确理解题意构造相应的不等式是本题的解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
