3.1勾股定理同步练习(含解析) 苏科版数学八年级上册
文档属性
| 名称 | 3.1勾股定理同步练习(含解析) 苏科版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-15 07:31:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.1勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平面直角坐标系中,点和点.则P、Q两点间的距离的最小值为( )
A.2 B. C.4 D.5
2.如图,在矩形中,于点E,,则的长为( )
A. B.2 C. D.
3.图1是第七届国际数学教育大会()的会徽,主体图案是由如图2的一连串直角三角形演化而成,其中.若,则的值为( )
A. B.2 C. D.1
4.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A.56 B.48 C.40 D.32
5.下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.,, C.3,4,6 D.4,5,6
6.如图,在中,,,按以下步骤作图:第一步,以点为圆心,适当的长为半径作弧,分别交,于、两点;第二步,分别以点、为圆心,大于的长为半径作弧,两弧相交于点;第三步,作射线,交于点.则的长为( )
A. B.8 C. D.10
7.如图,在中,,点是上一点,平分,过点作垂足为点,若,则的长是( )
A. B. C. D.
8.在直角三角形中,若两条直角边的长分别是1cm、2cm,则斜边的长为( )cm.
A.3 B. C.2或 D.或
9.如图,在中,,为的中线,为的中线,且,若,则的面积为( )
A. B. C. D.
10.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5 B.2.4 C.2.5 D.3.5
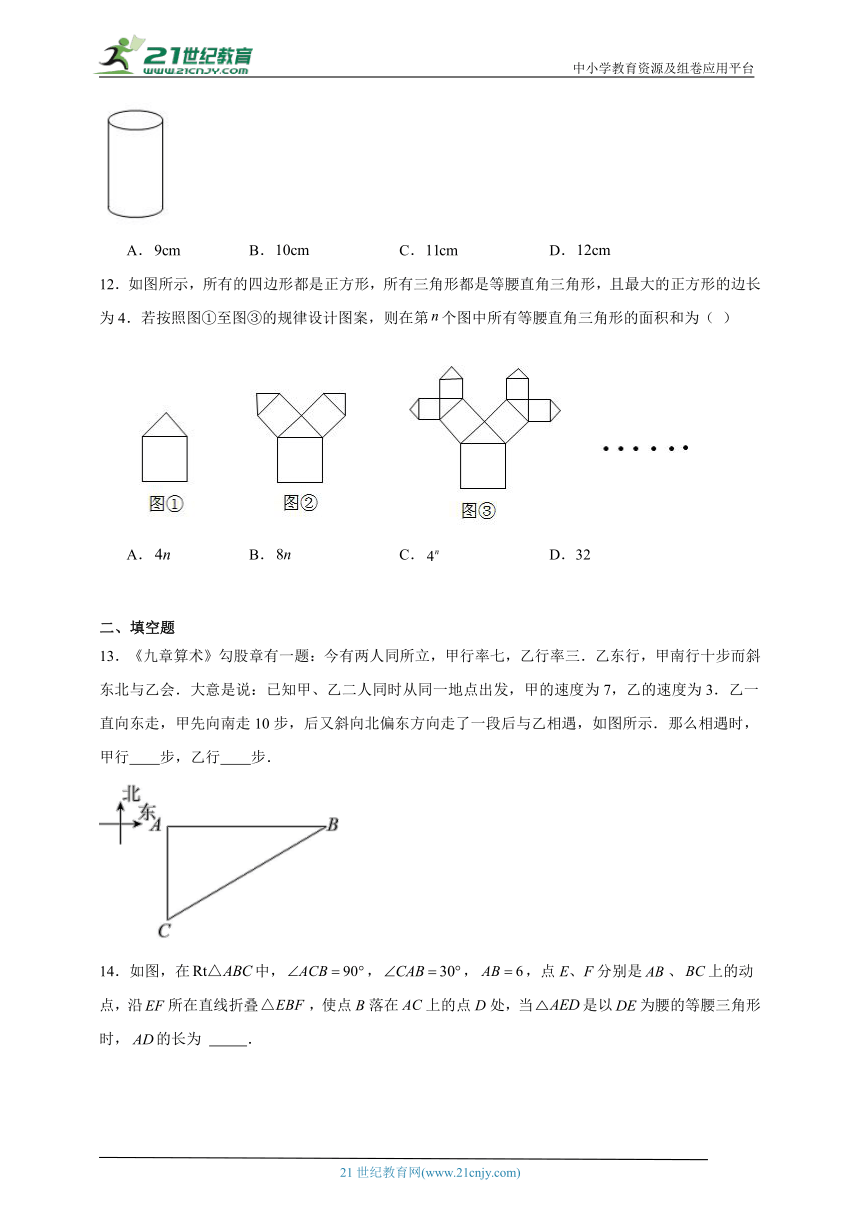
11.如图所示的圆柱形杯子的内直径为,内部高度为,小颖把一根直吸管放入杯中,要使吸管不斜滑到杯里,则吸管的长度(整厘米数)最短是( )
A. B. C. D.
12.如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第个图中所有等腰直角三角形的面积和为( )
A. B. C. D.32
二、填空题
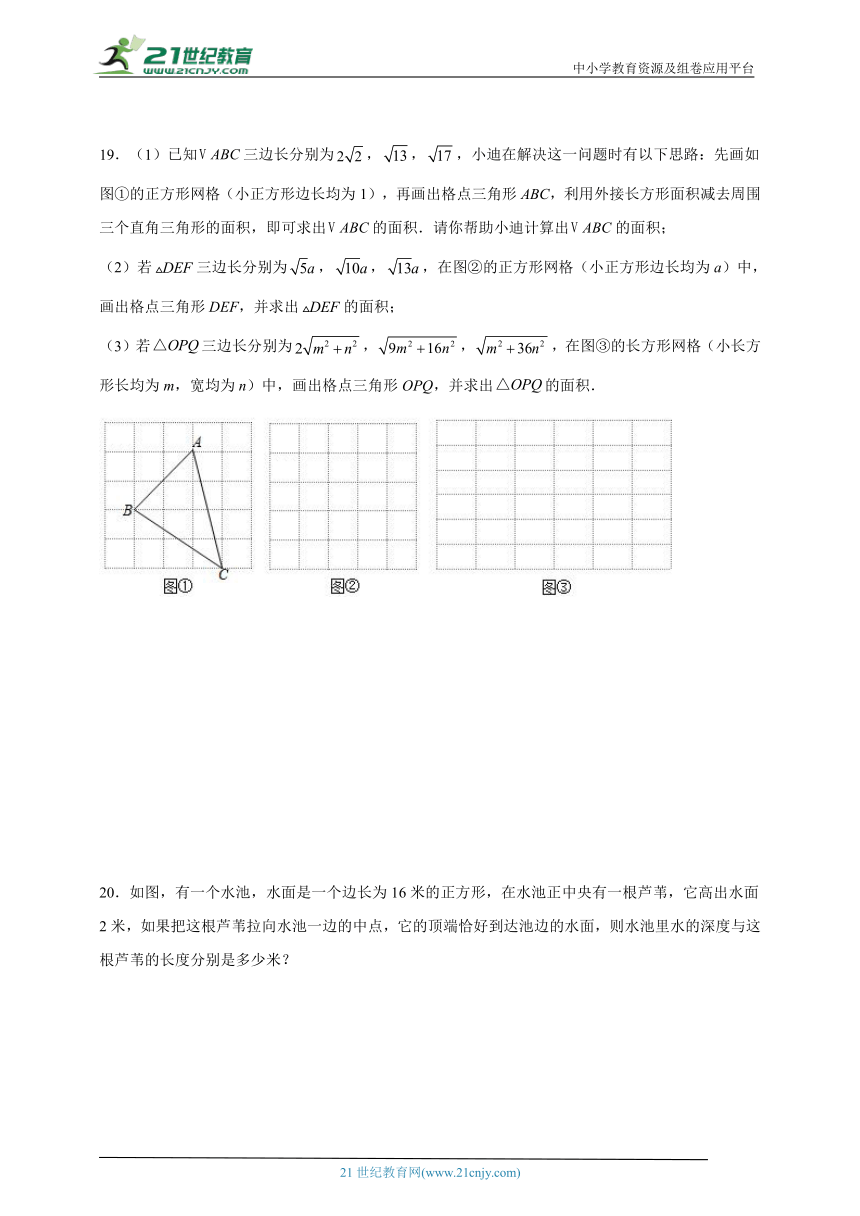
13.《九章算术》勾股章有一题:今有两人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇,如图所示.那么相遇时,甲行 步,乙行 步.
14.如图,在中,,,,点E、F分别是、上的动点,沿所在直线折叠,使点B落在上的点D处,当是以为腰的等腰三角形时,的长为 .
15.在中,,点D是线段上的动点,连接,以线段为直角边如图所示作等腰直角三角形,则周长的最小值为 .
16.在Rt△ABC中,,,,则AC= .
17.如图,阴影部分是一个正方形,则这个正方形的面积为 .
三、解答题
18.把一个直立的火柴盒放倒(如图),请你用不同的方法计算梯形ACED的面积,再次验证勾股定理?(设火柴盒截面宽为a,长为b,对角线为c)
19.(1)已知三边长分别为,,,小迪在解决这一问题时有以下思路:先画如图①的正方形网格(小正方形边长均为1),再画出格点三角形ABC,利用外接长方形面积减去周围三个直角三角形的面积,即可求出的面积.请你帮助小迪计算出的面积;
(2)若三边长分别为,,,在图②的正方形网格(小正方形边长均为a)中,画出格点三角形DEF,并求出的面积;
(3)若三边长分别为,,,在图③的长方形网格(小长方形长均为m,宽均为n)中,画出格点三角形OPQ,并求出的面积.
20.如图,有一个水池,水面是一个边长为16米的正方形,在水池正中央有一根芦苇,它高出水面2米,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,则水池里水的深度与这根芦苇的长度分别是多少米?
21.如 图 , 四 边 形 为某工厂的平面图 , 经 测 量米,且,.(参考数据: , )
(1)求的长;(结果精确到1米)
(2)若直线为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点D 处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为米, 求被监控到的道路长度为多少米?
22.如图,小明在山下E处发现正前方山上有个电视塔,测得塔尖C的仰角为,小明朝正前方笔直行走到达F处,此时测得塔尖C的仰角为,若小明的眼睛离地面,请算出这个电视塔塔尖离地面的高度(结果保留根号).
23.如图,长方形纸片,,,现将该纸片折叠,使点C与点A重合,折痕为,
(1)试判断的形状,并说明理由;
(2)求线段的长;
(3)求折痕的长.
24.在中,是的中点,是上一点,连接并延长使.
(1)证明:;
(2)若,,平分,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A B B A B B B B
题号 11 12
答案 C A
1.C
【分析】根据两点间的距离公式计算即可.
【详解】解:P、Q两点间的距离为,
∵,
∴P、Q两点间的距离的最小值为,
故答案为:C.
【点睛】本题主要考查了两点间的距离,明确是解题的关键.
2.D
【分析】由矩形的性质得出,得出,由已知条件得出,,由线段垂直平分线的性质得出,得出为等边三角形,因此,由三角形的外角性质得出,由含角的直角三角形的性质即可得出的长.
【详解】解:∵四边形是矩形,
∴,
∴,
∴,
∵,
∴
∴又
故点D在线段的垂直平分线上.
∴,
∴,
∴为等边三角形,
∴,
∴,
∵在中,,
∴,
∴,
∴.
故选:D.
【点睛】本题考查了矩形的性质,等边三角形的判定和性质,直角三角形的性质,线段垂直平分线的性质,证明是等边三角形是本题的关键.
3.A
【分析】根据勾股定理得到,,找到的规律,列方程即可得到结论.
【详解】解:∵,,,
∴,
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查了勾股定理,图形类找规律,本题中找到的规律是解题的关键.
4.B
【分析】根据题意画出图形,进而利用勾股定理得出DC的长,进而求出BC的长,即可得出答案.
【详解】解:过点A做AD⊥BC于点D,
∵等腰三角形底边上的高为8,周长为32,
∴AD=8,设DC=BD=x,则AB=(32﹣2x)=16﹣x,
∴AC2=AD2+DC2,即(16﹣x)2=82+x2,
解得:x=6,
故BC=12,
则△ABC的面积为:×AD×BC=×8×12=48.
故选B.
考点:勾股定理;等腰三角形的性质.
5.B
【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、12+22≠32,故不能组成直角三角形;
B、()2+()2=()2,故能组成直角三角形;
C、32+42≠62,故不能组成直角三角形;
D、42+52≠62,故不能组成直角三角形.
故选B.
【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
6.A
【分析】本题考查了作图基本作图,等腰三角形的“三线合一”定理,勾股定理,由等腰三角形的“三线合一”定理得到,,根据勾股定理即可求出.
【详解】解:由作法得是的平分线,
,
,,
在中,
.
故选:A.
7.B
【分析】直角三角形中30°角的性质,可得DE,运用角平分线的性质定理,可知CD=DE,再在直角三角形中运用勾股定理即可求得.
【详解】∵∠C=90°,
∴DC⊥AC,
∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴CD=DE,
在Rt△DEB中,∠B=30°,BD=2,
∴DE=BD=1,∴CD=1,
∵△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠CAD=∠CAB=30°,
在Rt△ACD中,CD=1,∠CAD=30°,
∴AD=2,
∴AC==,
故选B.
【点睛】本题考查角平分线的性质、勾股定理,难度较小,需熟练掌握基础知识.
8.B
【分析】根据勾股定理计算即可.
【详解】解:由勾股定理得,斜边长==,
故选:B.
【点睛】本题考查勾股定理,由于本题较简单,直接利用勾股定理解答即可.
9.B
【分析】此题考查等腰三角形的性质,勾股定理及三角形中位线性质;根据等腰三角形的性质和三角形中位线定理得出,进而利用勾股定理得出,进而利用三角形面积公式解答.
【详解】解:,为的中线,
,,
为的中线,
是的中位线,
,
由勾股定理可得,
的面积,
故选:B.
10.B
【分析】连接AM,根据等腰三角形三线合一的性质得到AM⊥BC,根据勾股定理求得AM的长,再根据在直角三角形的面积公式即可求得MN的长.
【详解】解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN AC=AM MC,
∴MN===2.4.
故选:B.
【点睛】综合运用等腰三角形的三线合一,勾股定理.特别注意结论:直角三角形斜边上的高等于两条直角边的乘积除以斜边.
11.C
【分析】运用勾股定理解题即可.
【详解】解:吸管长度为,
所以吸管的最短整数是,
故选C.
【点睛】本题考查勾股定理,掌握勾股定理的内容是解题的关键.
12.A
【分析】根据勾股定理求出等腰直角三角形直角边的长,求出每个图形中等腰三角形面积和,发现规律进而求出即可.
【详解】解:在图①中,正方形的边长为4,
∴等腰直角三角形①的直角边长为:
∴等腰直角三角形①的面积=
在图②中,最大的正方形的边长是4,最大的等腰直角三角形①的直角边长是
故可得等腰直角三角形②和③的直角边长都是2
∴
如图③,同理可求等腰直角三角形④⑤⑥⑦的直角边长均为
∴
=
=
=
=
由此可得规律:第n个图形中,所有等腰直角三角形的面积和为4n,
故选A.
【点睛】此题主要考查了运用勾股定理求等腰直角三角形直角边的长,解题的关键是求出每个图形中等腰直角三角形面积和.
13. 24.5 10.5
【分析】设经x秒后二人在B处相遇,然后利用勾股定理列出方程即可求得甲乙两人走的步数.
【详解】解:设经x秒后二人在B处相遇,这时乙共行,甲共行,
∵,
∴,
又∵,
∴,
∴,
∴,
∴,
,
∴甲走了步,乙走了步.
故答案为:,.
【点睛】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形.
14.或
【分析】分两种情况讨论:①当时,此时点C、点F重合,可得;②当时,此时点D、点C重合,可得,即可求出答案.
【详解】解:当是以为腰的三角形时,分两种情况:
①当时,如图1,
∵,
∴,
∴,
∴,
∵,且是由沿直线翻折得到,
根据翻折性质可得:,
∴点C、点F重合,
∵,,,
∴,
∴在中,由勾股定理得:
,
∵点C、点F重合,
∴,
∴;
②当时,如图2,
∵,
∴,
∵,且是由沿直线翻折得到,
根据翻折性质可得:,
∴点D、点C重合,
∴,
∵,,
∴,
∴在中,由勾股定理得:
,
∴;
故答案为:或.
【点睛】本题考查了动点问题求线段长度,涉及到直角三角形的性质和勾股定理、折叠的性质和等腰三角形的性质和判定,运用分类讨论思想是解题关键.
15.
【分析】取的中点F,连接,证明出,得到,作点C关于的对称点G,连接与的交点为D,此时的周长最小,过点G作交于点K,连接,然后利用等面积法和勾股定理求解即可.
【详解】取的中点F,连接
∵
∴
∵
∴
∵
∴
∵是等腰直角三角形
∴
∴
∴
∴的周长
作点C关于的对称点G,连接与的交点为D,
由对称性可得,
∴,此时的周长最小
过点G作交于点K,连接
∵是的垂直平分线
∴
在中,
∴,
∴
∴,
∴,
在中,,
在中,
∴
∴
∴在中,
∴
在中,
∴的周长的最小值为.
故答案为:.
【点睛】此题考查了轴对称求最短距离,勾股定理,等腰直角三角形的性质,垂直平分线的性质等知识,解题的关键是掌握以上知识点.
16..
【分析】先根据题意画出图形,先依据含直角三角形的性质求得的长,然后依据勾股定理可求得的长.
【详解】解:如图示:
,,,
,
.
故答案是:.
【点睛】本题主要考查的是含的直角三角形的性质和勾股定理的应用,熟悉相关性质是解题的关键.
17.9
【分析】先根据勾股定理求出正方形的边长,然后再求面积即可.
【详解】解:∵正方形的边长为(cm),
∴正方形的面积为32=9cm2.
故答案为9.
【点睛】本题主要考查了勾股定理的定义,正确运用勾股定理解直角三角形是解答本题的关键.
18.见解析.
【分析】四边形ACED的面积从大的一方面来说属于直角梯形,可利用直角梯形面积公式进行表示;从组成来看,由三个直角三角形组成,应利用三角形的面积公式来进行表示.
【详解】
【点睛】本题考查勾股定理的证明,利用面积的不同表示方式列出等式是解答本题的关键.
19.(1)5;(2)作图见解析,;(3)作图见解析,
【分析】(1)用长为4宽为3的长方形面积减去周围三个三角形的面积求解即可;
(2)先根据勾股定理的确定周围三个三角形的边长,再作图即可,再利用外接长方形面积减去周围三个直角三角形的面积,即可求出面积;
(3)先根据勾股定理的确定周围三个三角形的边长,再作图即可,再利用外接长方形面积减去周围三个直角三角形的面积,即可求出面积.
【详解】(1)的面积,
所以,的面积为5;
(2)是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,
作图如下:
的面积;
(3)是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,
格点三角形OPQ如图所示:
的面积.
【点睛】本题考查了勾股定理的应用及三角形的面积问题,熟练掌握知识点是解题的关键.
20.水的深度是15米,芦苇长为17米
【分析】本题主要考查了勾股定理的实际应用,熟练地掌握勾股定理是解题的关键.利用勾股定理构造方程求解即可.
【详解】解:设水池里水的深度是x米,则芦苇长为米,
由题意得,,
解得:,
,
答:水池里水的深度是15米,芦苇长为17米
21.(1)138米
(2)160米
【分析】本题考查了勾股定理的应用以及等腰直角三角形的判定与性质等知识,熟练掌握勾股定理是解题的关键.
(1)根据等腰直角三角形的性质得出,进而利用勾股定理逆定理解答即可;
(2)根据勾股定理解答即可.
【详解】(1)解:连接,
,且,
为等腰直角三角形,
,;
,
,
为直角三角形,
,
即的长为138米;
(2)解:如图,过点D作于E,设 P、Q为直线上监控到的最远点,
∴;
∵,
∴,
是等腰直角三角形,
,
摄像头能监控的最远距离为米,,
,
,
即被监控到的道路长度为160米.
22.
【分析】首先由三角形外角的性质得到,然后求出,然后利用含角直角三角形的性质求出,然后利用勾股定理求解即可.
【详解】由题意得:四边形是矩形,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,
∴.
【点睛】此题考查了含角直角三角形的性质,勾股定理,等角对等边,三角形外角的性质,解题的关键是掌握以上知识点.
23.(1)为等腰三角形,理由见详解
(2)
(3)
【分析】本题主要考查折叠的性质、全等三角形的性质与判定及勾股定理,熟练掌握折叠的性质及勾股定理是解题的关键;
(1)由折叠的性质可知,然后可得,进而问题可求解;
(2)设,则有,然后根据勾股定理可建立方程进行求解;
(3)过点E作于点H,由题意易得,然后可得,进而根据勾股定理可进行求解.
【详解】(1)解:为等腰三角形,理由如下:
由折叠的性质可知,,
在长方形中,,
∴,
∴,即为等腰三角形;
(2)解:在长方形中,,
由(1)可设,则有,
在中,由勾股定理得:,
解得:,
∴;
(3)解:过点E作于点H,如图所示:
在长方形中,,,
∴,
∵,
∴,
∴,
∴,
∴.
24.(1)见详解
(2)3
【分析】本题主要考查了全等三角形的判定与性质、平行线的判定、等腰三角形的判定与性质、勾股定理等知识,熟练掌握全等三角形的性质和等腰三角形的性质是解题关键.
(1)证明,由全等三角形的性质可得,然后证明结论即可;
(2)证明为等腰三角形,由等腰三角形“三线合一”的性质可得,,然后利用勾股定理求解即可.
【详解】(1)证明:∵是的中点,
∴,
在和中,
,
∴,
∴,
∴;
(2)解:∵平分,
∴,
由(1)可知,,
∴,
∴,即为等腰三角形,
∵是的中点,,,
∴,,
∴在中,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.1勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.平面直角坐标系中,点和点.则P、Q两点间的距离的最小值为( )
A.2 B. C.4 D.5
2.如图,在矩形中,于点E,,则的长为( )
A. B.2 C. D.
3.图1是第七届国际数学教育大会()的会徽,主体图案是由如图2的一连串直角三角形演化而成,其中.若,则的值为( )
A. B.2 C. D.1
4.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A.56 B.48 C.40 D.32
5.下列选择中,是直角三角形的三边长的是( )
A.1,2,3 B.,, C.3,4,6 D.4,5,6
6.如图,在中,,,按以下步骤作图:第一步,以点为圆心,适当的长为半径作弧,分别交,于、两点;第二步,分别以点、为圆心,大于的长为半径作弧,两弧相交于点;第三步,作射线,交于点.则的长为( )
A. B.8 C. D.10
7.如图,在中,,点是上一点,平分,过点作垂足为点,若,则的长是( )
A. B. C. D.
8.在直角三角形中,若两条直角边的长分别是1cm、2cm,则斜边的长为( )cm.
A.3 B. C.2或 D.或
9.如图,在中,,为的中线,为的中线,且,若,则的面积为( )
A. B. C. D.
10.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A.1.5 B.2.4 C.2.5 D.3.5
11.如图所示的圆柱形杯子的内直径为,内部高度为,小颖把一根直吸管放入杯中,要使吸管不斜滑到杯里,则吸管的长度(整厘米数)最短是( )
A. B. C. D.
12.如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第个图中所有等腰直角三角形的面积和为( )
A. B. C. D.32
二、填空题
13.《九章算术》勾股章有一题:今有两人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.大意是说:已知甲、乙二人同时从同一地点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇,如图所示.那么相遇时,甲行 步,乙行 步.
14.如图,在中,,,,点E、F分别是、上的动点,沿所在直线折叠,使点B落在上的点D处,当是以为腰的等腰三角形时,的长为 .
15.在中,,点D是线段上的动点,连接,以线段为直角边如图所示作等腰直角三角形,则周长的最小值为 .
16.在Rt△ABC中,,,,则AC= .
17.如图,阴影部分是一个正方形,则这个正方形的面积为 .
三、解答题
18.把一个直立的火柴盒放倒(如图),请你用不同的方法计算梯形ACED的面积,再次验证勾股定理?(设火柴盒截面宽为a,长为b,对角线为c)
19.(1)已知三边长分别为,,,小迪在解决这一问题时有以下思路:先画如图①的正方形网格(小正方形边长均为1),再画出格点三角形ABC,利用外接长方形面积减去周围三个直角三角形的面积,即可求出的面积.请你帮助小迪计算出的面积;
(2)若三边长分别为,,,在图②的正方形网格(小正方形边长均为a)中,画出格点三角形DEF,并求出的面积;
(3)若三边长分别为,,,在图③的长方形网格(小长方形长均为m,宽均为n)中,画出格点三角形OPQ,并求出的面积.
20.如图,有一个水池,水面是一个边长为16米的正方形,在水池正中央有一根芦苇,它高出水面2米,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,则水池里水的深度与这根芦苇的长度分别是多少米?
21.如 图 , 四 边 形 为某工厂的平面图 , 经 测 量米,且,.(参考数据: , )
(1)求的长;(结果精确到1米)
(2)若直线为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点D 处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为米, 求被监控到的道路长度为多少米?
22.如图,小明在山下E处发现正前方山上有个电视塔,测得塔尖C的仰角为,小明朝正前方笔直行走到达F处,此时测得塔尖C的仰角为,若小明的眼睛离地面,请算出这个电视塔塔尖离地面的高度(结果保留根号).
23.如图,长方形纸片,,,现将该纸片折叠,使点C与点A重合,折痕为,
(1)试判断的形状,并说明理由;
(2)求线段的长;
(3)求折痕的长.
24.在中,是的中点,是上一点,连接并延长使.
(1)证明:;
(2)若,,平分,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A B B A B B B B
题号 11 12
答案 C A
1.C
【分析】根据两点间的距离公式计算即可.
【详解】解:P、Q两点间的距离为,
∵,
∴P、Q两点间的距离的最小值为,
故答案为:C.
【点睛】本题主要考查了两点间的距离,明确是解题的关键.
2.D
【分析】由矩形的性质得出,得出,由已知条件得出,,由线段垂直平分线的性质得出,得出为等边三角形,因此,由三角形的外角性质得出,由含角的直角三角形的性质即可得出的长.
【详解】解:∵四边形是矩形,
∴,
∴,
∴,
∵,
∴
∴又
故点D在线段的垂直平分线上.
∴,
∴,
∴为等边三角形,
∴,
∴,
∵在中,,
∴,
∴,
∴.
故选:D.
【点睛】本题考查了矩形的性质,等边三角形的判定和性质,直角三角形的性质,线段垂直平分线的性质,证明是等边三角形是本题的关键.
3.A
【分析】根据勾股定理得到,,找到的规律,列方程即可得到结论.
【详解】解:∵,,,
∴,
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查了勾股定理,图形类找规律,本题中找到的规律是解题的关键.
4.B
【分析】根据题意画出图形,进而利用勾股定理得出DC的长,进而求出BC的长,即可得出答案.
【详解】解:过点A做AD⊥BC于点D,
∵等腰三角形底边上的高为8,周长为32,
∴AD=8,设DC=BD=x,则AB=(32﹣2x)=16﹣x,
∴AC2=AD2+DC2,即(16﹣x)2=82+x2,
解得:x=6,
故BC=12,
则△ABC的面积为:×AD×BC=×8×12=48.
故选B.
考点:勾股定理;等腰三角形的性质.
5.B
【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.
【详解】解:A、12+22≠32,故不能组成直角三角形;
B、()2+()2=()2,故能组成直角三角形;
C、32+42≠62,故不能组成直角三角形;
D、42+52≠62,故不能组成直角三角形.
故选B.
【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.
6.A
【分析】本题考查了作图基本作图,等腰三角形的“三线合一”定理,勾股定理,由等腰三角形的“三线合一”定理得到,,根据勾股定理即可求出.
【详解】解:由作法得是的平分线,
,
,,
在中,
.
故选:A.
7.B
【分析】直角三角形中30°角的性质,可得DE,运用角平分线的性质定理,可知CD=DE,再在直角三角形中运用勾股定理即可求得.
【详解】∵∠C=90°,
∴DC⊥AC,
∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴CD=DE,
在Rt△DEB中,∠B=30°,BD=2,
∴DE=BD=1,∴CD=1,
∵△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠CAD=∠CAB=30°,
在Rt△ACD中,CD=1,∠CAD=30°,
∴AD=2,
∴AC==,
故选B.
【点睛】本题考查角平分线的性质、勾股定理,难度较小,需熟练掌握基础知识.
8.B
【分析】根据勾股定理计算即可.
【详解】解:由勾股定理得,斜边长==,
故选:B.
【点睛】本题考查勾股定理,由于本题较简单,直接利用勾股定理解答即可.
9.B
【分析】此题考查等腰三角形的性质,勾股定理及三角形中位线性质;根据等腰三角形的性质和三角形中位线定理得出,进而利用勾股定理得出,进而利用三角形面积公式解答.
【详解】解:,为的中线,
,,
为的中线,
是的中位线,
,
由勾股定理可得,
的面积,
故选:B.
10.B
【分析】连接AM,根据等腰三角形三线合一的性质得到AM⊥BC,根据勾股定理求得AM的长,再根据在直角三角形的面积公式即可求得MN的长.
【详解】解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN AC=AM MC,
∴MN===2.4.
故选:B.
【点睛】综合运用等腰三角形的三线合一,勾股定理.特别注意结论:直角三角形斜边上的高等于两条直角边的乘积除以斜边.
11.C
【分析】运用勾股定理解题即可.
【详解】解:吸管长度为,
所以吸管的最短整数是,
故选C.
【点睛】本题考查勾股定理,掌握勾股定理的内容是解题的关键.
12.A
【分析】根据勾股定理求出等腰直角三角形直角边的长,求出每个图形中等腰三角形面积和,发现规律进而求出即可.
【详解】解:在图①中,正方形的边长为4,
∴等腰直角三角形①的直角边长为:
∴等腰直角三角形①的面积=
在图②中,最大的正方形的边长是4,最大的等腰直角三角形①的直角边长是
故可得等腰直角三角形②和③的直角边长都是2
∴
如图③,同理可求等腰直角三角形④⑤⑥⑦的直角边长均为
∴
=
=
=
=
由此可得规律:第n个图形中,所有等腰直角三角形的面积和为4n,
故选A.
【点睛】此题主要考查了运用勾股定理求等腰直角三角形直角边的长,解题的关键是求出每个图形中等腰直角三角形面积和.
13. 24.5 10.5
【分析】设经x秒后二人在B处相遇,然后利用勾股定理列出方程即可求得甲乙两人走的步数.
【详解】解:设经x秒后二人在B处相遇,这时乙共行,甲共行,
∵,
∴,
又∵,
∴,
∴,
∴,
∴,
,
∴甲走了步,乙走了步.
故答案为:,.
【点睛】本题考查了勾股定理的应用,解题的关键是从实际问题中抽象出直角三角形.
14.或
【分析】分两种情况讨论:①当时,此时点C、点F重合,可得;②当时,此时点D、点C重合,可得,即可求出答案.
【详解】解:当是以为腰的三角形时,分两种情况:
①当时,如图1,
∵,
∴,
∴,
∴,
∵,且是由沿直线翻折得到,
根据翻折性质可得:,
∴点C、点F重合,
∵,,,
∴,
∴在中,由勾股定理得:
,
∵点C、点F重合,
∴,
∴;
②当时,如图2,
∵,
∴,
∵,且是由沿直线翻折得到,
根据翻折性质可得:,
∴点D、点C重合,
∴,
∵,,
∴,
∴在中,由勾股定理得:
,
∴;
故答案为:或.
【点睛】本题考查了动点问题求线段长度,涉及到直角三角形的性质和勾股定理、折叠的性质和等腰三角形的性质和判定,运用分类讨论思想是解题关键.
15.
【分析】取的中点F,连接,证明出,得到,作点C关于的对称点G,连接与的交点为D,此时的周长最小,过点G作交于点K,连接,然后利用等面积法和勾股定理求解即可.
【详解】取的中点F,连接
∵
∴
∵
∴
∵
∴
∵是等腰直角三角形
∴
∴
∴
∴的周长
作点C关于的对称点G,连接与的交点为D,
由对称性可得,
∴,此时的周长最小
过点G作交于点K,连接
∵是的垂直平分线
∴
在中,
∴,
∴
∴,
∴,
在中,,
在中,
∴
∴
∴在中,
∴
在中,
∴的周长的最小值为.
故答案为:.
【点睛】此题考查了轴对称求最短距离,勾股定理,等腰直角三角形的性质,垂直平分线的性质等知识,解题的关键是掌握以上知识点.
16..
【分析】先根据题意画出图形,先依据含直角三角形的性质求得的长,然后依据勾股定理可求得的长.
【详解】解:如图示:
,,,
,
.
故答案是:.
【点睛】本题主要考查的是含的直角三角形的性质和勾股定理的应用,熟悉相关性质是解题的关键.
17.9
【分析】先根据勾股定理求出正方形的边长,然后再求面积即可.
【详解】解:∵正方形的边长为(cm),
∴正方形的面积为32=9cm2.
故答案为9.
【点睛】本题主要考查了勾股定理的定义,正确运用勾股定理解直角三角形是解答本题的关键.
18.见解析.
【分析】四边形ACED的面积从大的一方面来说属于直角梯形,可利用直角梯形面积公式进行表示;从组成来看,由三个直角三角形组成,应利用三角形的面积公式来进行表示.
【详解】
【点睛】本题考查勾股定理的证明,利用面积的不同表示方式列出等式是解答本题的关键.
19.(1)5;(2)作图见解析,;(3)作图见解析,
【分析】(1)用长为4宽为3的长方形面积减去周围三个三角形的面积求解即可;
(2)先根据勾股定理的确定周围三个三角形的边长,再作图即可,再利用外接长方形面积减去周围三个直角三角形的面积,即可求出面积;
(3)先根据勾股定理的确定周围三个三角形的边长,再作图即可,再利用外接长方形面积减去周围三个直角三角形的面积,即可求出面积.
【详解】(1)的面积,
所以,的面积为5;
(2)是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,
作图如下:
的面积;
(3)是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,是直角边长分别为的直角三角形的斜边长,
格点三角形OPQ如图所示:
的面积.
【点睛】本题考查了勾股定理的应用及三角形的面积问题,熟练掌握知识点是解题的关键.
20.水的深度是15米,芦苇长为17米
【分析】本题主要考查了勾股定理的实际应用,熟练地掌握勾股定理是解题的关键.利用勾股定理构造方程求解即可.
【详解】解:设水池里水的深度是x米,则芦苇长为米,
由题意得,,
解得:,
,
答:水池里水的深度是15米,芦苇长为17米
21.(1)138米
(2)160米
【分析】本题考查了勾股定理的应用以及等腰直角三角形的判定与性质等知识,熟练掌握勾股定理是解题的关键.
(1)根据等腰直角三角形的性质得出,进而利用勾股定理逆定理解答即可;
(2)根据勾股定理解答即可.
【详解】(1)解:连接,
,且,
为等腰直角三角形,
,;
,
,
为直角三角形,
,
即的长为138米;
(2)解:如图,过点D作于E,设 P、Q为直线上监控到的最远点,
∴;
∵,
∴,
是等腰直角三角形,
,
摄像头能监控的最远距离为米,,
,
,
即被监控到的道路长度为160米.
22.
【分析】首先由三角形外角的性质得到,然后求出,然后利用含角直角三角形的性质求出,然后利用勾股定理求解即可.
【详解】由题意得:四边形是矩形,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵,
∴.
【点睛】此题考查了含角直角三角形的性质,勾股定理,等角对等边,三角形外角的性质,解题的关键是掌握以上知识点.
23.(1)为等腰三角形,理由见详解
(2)
(3)
【分析】本题主要考查折叠的性质、全等三角形的性质与判定及勾股定理,熟练掌握折叠的性质及勾股定理是解题的关键;
(1)由折叠的性质可知,然后可得,进而问题可求解;
(2)设,则有,然后根据勾股定理可建立方程进行求解;
(3)过点E作于点H,由题意易得,然后可得,进而根据勾股定理可进行求解.
【详解】(1)解:为等腰三角形,理由如下:
由折叠的性质可知,,
在长方形中,,
∴,
∴,即为等腰三角形;
(2)解:在长方形中,,
由(1)可设,则有,
在中,由勾股定理得:,
解得:,
∴;
(3)解:过点E作于点H,如图所示:
在长方形中,,,
∴,
∵,
∴,
∴,
∴,
∴.
24.(1)见详解
(2)3
【分析】本题主要考查了全等三角形的判定与性质、平行线的判定、等腰三角形的判定与性质、勾股定理等知识,熟练掌握全等三角形的性质和等腰三角形的性质是解题关键.
(1)证明,由全等三角形的性质可得,然后证明结论即可;
(2)证明为等腰三角形,由等腰三角形“三线合一”的性质可得,,然后利用勾股定理求解即可.
【详解】(1)证明:∵是的中点,
∴,
在和中,
,
∴,
∴,
∴;
(2)解:∵平分,
∴,
由(1)可知,,
∴,
∴,即为等腰三角形,
∵是的中点,,,
∴,,
∴在中,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
